Математические задачи в пакете MathCAD 12

MathCAD

Синее и черное, или Задача Удодова

Марков снял сапоги и, вздохнув, лег на диван.
Ему хотелось спать, но, как только он закрывал глаза, желание спать моментально проходило. Марков открывал глаза и тянулся рукой за книгой. Но сон опять налетал на него, и, не дотянувшись до книги, Марков ложился и снова закрывал глаза. Но лишь только глаза закрывались, сон улетал опять, и сознание становилось таким ясным, что Марков мог в уме решать алгебраические задачи на уравнения с двумя неизвестными.
Даниил Хармс. «Сон дразнит человека»
Система алгебраических уравнений с двумя неизвестными для многих литераторов является вершиной математической премудрости. Вот еще одна цитата, дополняющая эпиграф первого этюда книги, – беседа чеховских персонажей: отставного губернского секретаря Удодова, его сына Пети и горе-репетитора Егора Зиберова, ученика VII класса гимназии:
Теперь по арифметике... Берите доску. Какая следующая задача?
Петя плюет на доску и стирает рукавом. Учитель берет задачник и диктует:
– «Купец купил 138 арш. черного и синего сукна за 540 руб. Спрашивается, сколько аршин купил он того и другого, если синее стоило 5 руб. за аршин, а черное 3 руб.?» Повторите задачу.
Петя повторяет задачу и тотчас же, ни слова не говоря, начинает делить 540 на 138.
– Для чего же вы это делите? Постойте! Впрочем, так... продолжайте. Остаток получается? Здесь не может быть остатка. Дайте-ка я разделю!
Зиберов делит, получает 3 с остатком и быстро стирает.
«Странно... – думает он, ероша волосы и краснея. – Как же она решается? Гм!.. Это задача на неопределенные уравнения, а вовсе не арифметическая...»
Учитель глядит в ответы и видит 75 и 63.
«Гм!.. странно... Сложить 5 и 3, а потом делить 540 на 8? Так, что ли? Нет, не то».
– Решайте же! – говорит он Пете.
– Ну, чего думаешь? Задача-то ведь пустяковая! – говорит Удодов Пете. – Экий ты дурак, братец! Решите уж вы ему, Егор Алексеич.
Егор Алексеич берет в руки грифель и начинает решать. Он заикается, краснеет, бледнеет.
– Это задача, собственно говоря, алгебраическая, – говорит он. – Ее с иксом и игреком решить можно. Впрочем, можно и так решить. Я, вот, разделил... понимаете? Теперь, вот, надо вычесть... понимаете? Или, вот что... Решите мне эту задачу сами к завтраму... Подумайте...

Петя ехидно улыбается. Удодов тоже улыбается. Оба они понимают замешательство учителя. Ученик VII класса еще пуще конфузится, встает и начинает ходить из угла в угол.
– И без алгебры решить можно, – говорит Удодов, протягивая руку к счетам и вздыхая. – Вот извольте видеть...
Он щелкает на счетах, и у него получается 75 и 63, что и нужно было.
– Вот-с... по-нашему, по-неученому.
Фрагмент из миниатюры А. П. Чехова «Репетитор» предварил наш рассказ о пакете Mathcad по трем причинам:
1. Описанная ситуация часто повторяется и сейчас. Только люди, решая задачи, стали протягивать руку не к счетам и даже не к калькулятору, а к персональному компьютеру. И самая подходящая на сегодняшний день программная среда для решения задач, подобных задаче Удодова, – это Mathcad.
2. Технология решения задач в среде Mathcad во многом похожа на подход Удодова-отца. Компьютеру достаточно сообщить условия задачи – и пусть себе решает, лишь бы ответ сошелся. О методах решения задач пользователь начинает задумываться, когда происходит осечка, что случается довольно редко, если иметь в виду не слишком сложные задачи (не суперзадачи, решение которых требует разработки специального матобеспечения).
3. И современная, и прошлого века – обратитесь еще раз к рассказу А. П. Чехова – методика преподавания школьной и вузовской математики, физики, химии и других предметов ориентирована, как правило, не на постановку задачи, а на решение уже кем-то сформулированных проблем. Компьютеризация школы (средней и высшей), базирующаяся на преподавании языков программирования (BASIC, Pascal, С и др.) в качестве основ информатики, ничего не меняет в этом не совсем нормальном положении вещей. Среды общения с ЭВМ на почти естественном для человека языке (и в то же время на математическом языке), к которым относится Mathcad, позволяют больше внимания уделять постановке проблемы, математическому моделированию реальных ситуаций, анализу ответа, а не методикам решения надуманных задач. К этому вопросу мы еще вернемся в этюде 7, когда речь пойдет о методике использования компьютеров на уроках математики – школьной и вузовской.
Но лучший способ оценить пакет Mathcad – это решить с его помощью задачу. А самый подходящий пример для начального знакомства с пакетом Mathcad – чеховская задача. Вот три отрывка из рассказа, определяющие три возможных подхода к решению:
1. – И без алгебры решить можно, – говорит Удодов, протягивая руку к счетам и вздыхая. – Вот извольте видеть...
2. Петя повторяет задачу и тотчас же, ни слова не говоря, начинает делить 540 на 138.
3. – Это задача, собственно говоря, алгебраическая, – говорит он (Зиберов). – Ее с иксом и игреком решить можно.
Ниже читатель может увидеть эти три решения задачи о купце и сукне: Удодова-отца (рис. 1.1, 1.4 и 1.5), Петин (рис. 1.6) и Зиберовский (рис. 1.7), реализованные в среде Mathcad.

Задача о балке, или Вариации на тему русской пословицы

Лучше один раз увидеть [протокол решения задачи], чем сто раз услышать [о возможностях пакета] – следуя такому «расширению» пословицы, рассмотрим решение в среде Mathcad классической задачи теоретической механики из раздела «Статика» – задачи о равновесии балки.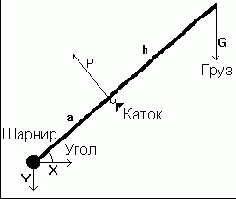

Великолепная семерка Mathcad

Раз уж мы залезли в мистику (в описание магических свойств числа семь), то подошла пора рассказа о великолепной семерке
Mathcad – о семи видах графиков, используемых для визуального отображения различных зависимостей. Типов графиков в Mathcad, конечно, намного больше, но на панели инструментов имеется ровно семь кнопок для создания семи типов графиков. Мистика, да и только.
Графики очень помогают решать поставленные задачи. На рис. 1.8, например, начальные приближения к корню системы брались вблизи точек пересечения линий на графике. Глядя на выражение, можно узреть там корни, минимумы, максимумы и прочие интересные точки, только обладая сильно извращенным математикой воображением. На графике же все видно как на ладони.
К сожалению, графики, помещенные в книге, черно-белые. Их можно было бы расцветить, как это имеет место на экране дисплея, но цена книги от этого резко увеличилась бы. А ведь она адресована студентам и инженерам (см. название). Сейчас автор пишет книгу под условным названием «Mathcad для «новых» русских» с цветными иллюстрациями. Есть уже первые задачи для нее – задача о купце и сукне (см. рис. 1.14), задача о качестве менеджера (рис. 4.6 и 4.17) и задача о финансовой пирамиде (рис. 5.4) и др.
Но вернемся к графике.
Если нажать соответствующую кнопку панели инструментов (см. рис. 1.2 и 1.3), то раскроется панель графики с девятью новыми кнопками (см. рис. 1.17).
Нажимая на них, можно построить семь типов графиков. Сделаем это для иллюстрации решения задачи о балке, схема которой помещена на рис. 1.12.
На рис. 1.17-1.19 и 1.21-1.25 графически отображены реакции опор балки в зависимости от угла ее наклона при фиксированных других параметрах. Функциональные зависимости x, y и P (реакции опор – см. пункт 2 на рис. 1.17, пункт 5 на рис. 1.20, пункт 8 на рис. 1.24 и пункт 9 на рис. 1.25) взяты из главы 7, где наша система, описывающая равновесие балки, решается аналитически (см. рис. 7.9).

Операторы и функции

В математике есть основополагающее понятие – соотношение: имеется два множества; каждому элементу первого множества соотносят элемент второго множества. Частным случаем такого соотношения является функция одного аргумента – каждому значению угла (первое множество) соответствует значение, например, синуса (второе множество), косинуса и т.д. Читатель средних лет тут сразу вспомнит знаменитые таблицы Брадиса с такими «множествами» углов, синусов, логарифмов и других нужных для расчетов данных. Естественно, Mathcad не хранит множество углов и множество соответствующих им синусов, а рассчитывает эту тригонометрическую функцию по определенному алгоритму. Насколько он точен и быстр – это второй вопрос.
Можно говорить о двух множествах чисел, одном множестве функций и еще об одном множестве переменных и о множестве значений определенного интеграла: каждой четверке элементов первых четырех множеств соответствует один элемент пятого множества. Здесь речь идет об операторе определенного интеграла с четырьмя операндами, который также есть в среде Mathcad.
Лет двадцать назад наметилось некое несоответствие в трактовке терминов «функция», «оператор» математиками и программистами[24].
Математик, читая эту книгу, может сделать абсолютно законный вывод, что автор не вполне понимает, что такое оператор и что такое функция. Более того, в самом программировании нет полного единства в определении этих основополагающих понятий. То, что мы называем оператором в среде Mathcad, в среде языка BASIC называется иначе, и наоборот. Так, в среде языка BASIC есть очень удобный оператор Swap(a, b), меняющий в переменных a и b их содержимое. Этот оператор ничего не возвращает и, следовательно, с точки зрения пользователя Mathcad не может называться оператором. С другой стороны, операторы и функции Mathcad сами по себе тоже могут ничего не возвращать, а просто находиться в Mathcad-документе и ждать, когда с ними что-нибудь сделают. Например, поместят в левый операнд оператора вывода числового значения. Вот тогда-то они начнут возвращать то, что записано в приложениях 2 и 3.

Будем считать, что термины «оператор» и «функция» программно-зависимы, и рассмотрим не их суть (об этом пусть спорят теоретики), а отличия друг от друга в среде Mathcad.
Вот тест на внимательность читателя: заметил ли он разницу в использовании тригонометрических функций sin и cos на рис. 1.15 и 1.16. На первом рисунке аргумент a заключен в скобки, а на втором – нет. На рис. 1.16 можно было бы написать более экзотически (по-арабски): a sin и a cos.
Дело в том, что вычисление синуса и косинуса на рис. 1.15 ведется через вызов функции, а на рис. 1.16 – через вызов оператора. Для компьютера нет никакой разницы между функцией и оператором: и в том и в другом случае все сводится к вызову соответствующей вычислительной процедуры. Разница важна для пользователя, который еще в школе на уроках математики привык, что сложение, например, – это оператор с двумя операндами: 2 + 5, а синус – функция с одним аргументом: sin(a). Но ничто не мешает нам складывать через вызов функции (встроенной или пользовательской):
сложить(a, b):= a + b
сложить(2, 5)=7,
а рассчитывать синус и косинус через вызов оператора – см. рис. 1.16.
Функции вводятся в документ, как правило, через нажатие соответствующих кнопок: «s», «i», «n», «(» и т.д. Но лучше для этого использовать «мастер функций» (рис. 1.28).

A philosophical-religious aspect of the problem

A naturalist interested in a real-world phenomenon has no ability to appeal straight to the Creator (God or Nature, according to your choice) but has to ask the research object itself – that is, carry out an experiment by perturbing this object and investigating its reaction.
A program has its own creators, the authors. Their names are not always specified on boxes, disks and in the documentation, but they do exist. Hence – theoretically – it should be unnecessary to experiment with programs. All questions that may arise ought to be answerable either by the documentation or the authors themselves. But – in practice – if a user wishes, for instance, to identify the measurement unit (degrees or radians) of a sine function, they won't rummage in the documentation. They will simply define x:= sin(90) and observe the x variable value.
Such experiments are carried out hourly by users, who appeal to the documentation only in extremely complicated cases, as a rule when they're not satisfied with their own answer. And it's rather problematic to appeal to the creator. The program dealers, not the authors, run the support hotline; and readers well know that this isn't the same thing. The hotline operator will most likely offer to test the program and try to find out the answer, and ask you to ring back in a couple of days. And it would often be ineffective to ask the authors, who have forgotten their offspring and are entirely engrossed in a new project. Even if that isn't so, they can't be expected to remember all the properties and nuances of their creation.
That is why users usually forget that a program is a product of human intelligence and skills, supposing – at an emotional level – that it's a fruit of the efforts of an anonymous and unattainable Creator who doesn't have a support hotline. Here, most probably, lies a philosophical explanation (but by no means justification) of the widespread practice of illegal program copying. We're not talking about deliberate larceny, like creating Chinese-Bulgarian CD-ROMs labelled "Everything for your Office".[1] Here, we are dealing with relatively honest people, installing a program on their computer from the above-mentioned CD-ROM in order to understand its nature and to share their knowledge, for instance with students.

One might think that the Creator, by throwing an apple from above and hitting Newton's head, had unveiled one of the mysteries of His Divine Plan. The genius, Newton, had the advantage of finding himself in the right place at the right time.[2]
Programs are also figuratively falling at our feet from above, under circumstances when one is not obliged to pay money, crazy amounts by Russian standards, for them. Hence a shareware ethos ensues, and it is dealers who primarily resist this idea, rather than the program authors.
The saying goes that God created Man in His own image, but it could be argued that this also applies to the computer. The program code is the soul breathed into a spiritless pile of magnetic iron. For humans, body trading (transplantation of organs, transfusion or, at last, prostitution) is the reality of contemporary life; traffic in souls is a matter for fairy tales and fiction (the Faust story, for example). When we purchase software, we are getting only a "body": disks, documentation, information and discounts for the new versions, and, chiefly, the after-sale service.

Гремим пожарными ведрами

Из круглой жестянки по несложной технологии изготавливается пожарное ведро (см. пункт 1 на рис. 2.1): вырезается сектор, затем полученная выкройка сворачивается в конус (точка a подтягивается к точке c), а шов сваривается (паяется).

Задача об оптимальном плане выпуска стульев

Суть задачи. Мебельная фабрика может выпускать стулья двух типов ценою в 8 и 12 условных единиц (у.е.[15]). Под этот заказ выделены материальные и людские ресурсы. Кроме того, известно, сколько досок, ткани и времени идет на изготовление каждого стула:

Стул		Расход досок, м		Расход ткани, м2		Расход времени, чел.-час.
Первый		2		0.5		2
Второй		4		0.25		2.5
Ресурс		490		65		320

Спрашивается, как нужно спланировать производство стульев, чтобы наделать их либо количеством, либо ценой поболее. Это и отображено в отчете о решении задачи на рис. 2.9.

Задача об оптимальных перевозках

На рис. 2.10 решается одна из разновидностей задач линейного программирования – транспортная задача: необходимо ежедневно с первого склада перевозить в два магазина 50 телевизоров[16], а со второго склада – 70. При этом первый магазин продает в день 40 телевизоров, а второй – 80 (50+70-40). В транспортной задаче неравенства в ограничениях заменены равенствами. Получается система линейных алгебраических уравнений, но не с одним, как в задаче о купце и сукне (см. рис. 1.6 и рис. 1.7) или в задаче о балке (см. рис. 1.15 и рис. 1.16), а с множеством решений, одно из которых оптимизирует целевую функцию. Известны затраты на перевозку одного телевизора со складов в магазины[17]
(четыре константы: 1200 у.е. при перевозке одного телевизора с первого склада в первый магазин, 1600 – с первого склада во второй магазин, 800 – со второго склада в первый магазин и 1000 – со второго склада во второй магазин).

A cultural aspect of the problem

Open the first page of any Western publication and you will notice the prohibition on duplication, whether chapters or pages, of the book. (I originally wrote "the formidable warning will strike your eye", but in the interest of neutrality replaced it with "you will notice"). Everyone is quite aware that only commercial duplication is meant here. Both Western and Russian libraries are quite legally equipped with photocopiers, which allow a book or a magazine to be 'xeroxed' from cover to cover, except maybe the very page with the formidable, but probably futile, warning. It is possible to duplicate the printed matter in every possible way for educational and scientific purposes (to copy an extract to an exercise book, for example).
Moreover, any hindrance for this kind of information distribution is regarded as a direct infringement of the rights of the author: not of the copyrights[3] but specifically "the rights of the author". But behind this phraseology is the fact that almost without exception, it is not the author controlling the copyright, but the publisher. The authorial rights are like human ones given 'from heaven', which can't be transferred to anyone. It is the copyright owner who is disappointed by the appearance of 'black' books on the market. The author (owner of the author's rights) may be at first flattered, but then he becomes worried about the future, but as a rule ephemeral, loss of profit[4].
The vagueness of the borders between commercial and non-commercial use can be illustrated by another fact. Suppose a graduate student has Xeroxed enough articles of other authors, and has sculpted from them a dissertation (let's be more tactful – a part of the dissertation) then received a scientific degree, and afterwards, with its help, a high-paid post in a firm or university. Even if "has sculpted from them" is replaced with "has used them as research material", the essence of the matter doesn't change: the knowledge is the most precious article in the civilised market.
Computer users are among the most avid reading public nowadays: not only adverts for romantic novels are flashing by in the Metro, but also those for various User Guides or "Excel for Dummies". This applies not only to printed matter but also to software, which is a programming product (production, products and similar are all marketing expressions). Studying a program is just as interesting and useful, culturally and educationally, as studying a book. A misfortune for programs, but perhaps a hidden blessing, is their easy copying. They can be duplicated much more easily than books. Furthermore, even the most ingenious programs are obsolete before the copyright expires, in contrast to the works of classical literature. Nowadays anyone nowadays can publish the undying compositions of Pushkin and Shakespeare.

Взгляд шутника

Есть особый род шутников (к ним относит себя и автор), получающих удовольствие от попыток розыгрыша компьютера. «Много ты, машина, о себе воображаешь. Посмотрим-ка, проглотишь ли ты вот это?!», – так или примерно так думают они, вводя в ЭВМ заведомо «неправильную» информацию. Анализ реакции компьютера (программной среды) на подобные шутки пользователя может дать не меньше, чем классический разбор программы.
В этюде будет рассмотрено решение в среде Mathcad задач из области вычислительной математики. Примеры взяты не из пакета Mathcad (хотя там есть схожие задачи), а из других источников, и подобраны так, чтобы можно было показать не только легкость и изящество их решения, но и возникающие при этом осложнения и пути их преодоления. К примерам, которые прилагают к пакетам фирмы-разработчики, следует относиться с большой опаской. Тут можно вспомнить эпохальную вычислительную машину «Наири», в матобеспечении которой была программа «Поиск минимума функций». Так вот, после опробования слово функций (множественное число) в ее названии приходилось менять на слово функции (единственное число), так как минимум искался только у приложенной к программе функции и больше ни у какой другой.

Взгляд дериватора

Есть особый род извращенцев… Автору не хватило духа вынести этот термин в заголовок этюда, и он заменил его нейтральным, производным от латинского derivatio (отклонение). Читатель, может быть, до этого места книги не доберется, а об авторе подумает черт знает что. Так вот, есть особый род дериваторов, получающих удовольствие от попыток решения задач программными средствами, для этих целей прямо не предназначенными.
– А вы ноктюрн сыграть смогли бы на флейте водосточных труб?!
– А вы тра-та-та та-та-ра-та бы в среде программы тра-та-та?!

Взгляд эстета

После выстрела и команды «Искать!» собака может вернуться к охотнику с тремя результатами:
1. Собака приносит подстреленную дичь.
2. Собака, израсходовав отпущенный лимит времени или услышав призывный сигнал охотника, возвращается с пустыми руками, пардон, зубами.
3. Охотник получает «трофей» – стреляный пыж или рваный башмак, но собачьи глаза и собачий хвост выдают собачью хитрость.
Есть особый род эстетов, получающих удовольствие от попыток облагораживания технического текста цитатами из художественной литературы. Но не этот смысл слова «эстет» подчеркнут в названии этюда. Автору уже не раз доводилось признаваться своим читателям, что для него в программной среде важны не только чисто технические параметры (быстродействие, богатство встроенных функций и т.д.), но и «красота» программы. Под красотой же следует понимать не только цветовую палитру или изящество окон и иконок, но и то наслаждение, которое программа может доставлять при решении даже простейших задач. И не только своими новыми, ранее неведомыми возможностями, но и своими... ошибками. Автор попытался было описать всю эту гамму чувств, но его опередил Карел Чапек своим рассказом «Игла», где необыкновенно точно передан дух расчетов – и не важно, проводятся ли они на бумаге или на компьютере. Помимо этого, чапековский отрывок поможет понять, при чем тут охотник:
Когда я работал в бухгалтерии и составлял, бывало, полугодовой отчет, подчас случалось, что цифры не сходятся. Однажды в наличности не хватило трех геллеров. Конечно, я мог просто положить в кассу эти три геллера, но это была бы неправильная игра. С бухгалтерской точки зрения это было бы неспортивно. Надо найти, в каком счете допущена ошибка, а счетов у нас было четырнадцать тысяч. И скажу вам, когда я брался за баланс, мне всегда хотелось, чтобы там обнаружилась какая-нибудь ошибка. Тогда я, бывало, оставался на службе хоть на всю ночь. Положу перед собой кучу бухгалтерских книг и берусь за дело. И для меня колонки цифр становились не цифрами, они преображались просто необыкновенно. То мне казалось, что я карабкаюсь по этим колонкам вверх, словно на крутую скалу, то я спускаюсь по ним, как по лестнице[35], в глубокую шахту. Иногда я чувствовал себя охотником, который продирается сквозь чащу цифр, чтобы изловить пугливого и редкого зверя – эти самые три геллера. И до того мне в такие минуты становилось хорошо от этого ощущения движения и силы, такое я чувствовал вокруг себя волнующее приволье, словно и в самом деле переживал необыкновенное приключение. Целыми ночами я мог охотиться за тремя геллерами, и когда находил их, то даже не думал, что это лишь жалкие гроши. Это была добыча, и я шел спать, торжествующий и счастливый...

Поиск решения с помощью функций root, Find, MinErr, Minimize и Maximize во многом напоминает ружейную охоту. Пользователь формирует анализируемую функцию, вводит ограничения, выставляет параметры поиска (заряжает ружье, выслеживает дичь), а затем нажимает клавишу F9 (спусковой крючок ружья). Собака (cреда Mathcad) прыгает в воду и возвращается с тремя результатами:
1. Решение найдено (см. пункт 4 рис. 3.1).
2. Решение не найдено (пункт 5).
3. Mathcad пытается подсунуть пользователю то, что только издали напоминает правильный результат (пункт 6).
При этом ситуация осложняется еще и тем, что пользователь Mathcad, в отличие от охотника, который знает, что такое дичь, часто не имеет понятия о том, что такое правильный результат. У среды Mathcad, к сожалению, нет глаз и хвоста, по которым можно определить, что именно принесено к ногам охотника – пользователя пакета.
Работа с функциями root, Find, MinErr, Minimize и Maximize – это хождение на охоту с чужой собакой, повадки которой неизвестны. «Своя собака» – это методы и алгоритмы, написанные на языке Mathcad и вставленные в документ, по которым решение ищется не вслепую, а наверняка (см. этюд 6). А если писать программы недосуг, то вот семь советов по работе с функциями root, Find, MinErr, Minimize и Maximize:
1. Найдя решение, еще раз заставьте Mathcad найти его уже от новой опорной точки. Неплохо при этом использовать одновременно все инструменты, заложенные в Mathcad. Из этюдов 2 и 3 мы знаем, что максимум, например, можно искать минимум тремя способами (нечаянный каламбур!): через поиск корней системы уравнений, составленных из частных производных анализируемой функции, с помощью функции MinErr и прямым способом – через функцию Maximize. Что здесь сработает – неизвестно, наверное, даже разработчикам Mathcad. Если из разных опорных точек разными методами найден один и тот же результат, то надо перекреститься и сказать: «Слава Богу! Задача решена!»


2. Перед решением оптимизационной задачи с ограничениями прогоните ее не с функцией MinErr, Minimize или Maximize, а с функцией Find для того, чтобы оценить область существования решений.
3. Начинайте поиск оптимального решения от одной из точек, найденных в пункте 2 и лежащих недалеко от оптимума.
4. Вводите ограничения постепенно: ввели первое – нашли какое-то подобие решения, ввели второе – уточнили его и т.д.
5. Начинайте решение оптимизационной задачи с целочисленными аргументами без ограничений на целочисленность. Нецелочисленный ответ всегда будет полезен, так как 1) от него можно начать поиск целочисленного решения, 2) можно удовлетвориться нецелочисленным решением (появление совместителя, например, в задаче об оптимальном штатном расписании) и 3) числа можно округлить вручную, если целочисленное решение отыскать невозможно.
6. Проверяйте правильность найденных корней, минимумов и максимумов построением графиков и поверхностей, где эти точки видны, благо пакет Mathcad имеет богатый набор графики. Если аргументов у функции больше двух, постройте графики сечений через точку оптимума (рис. 3.5) по всем координатам и убедитесь, что там все частные производные равны нулю. Неплохо тут протабулировать анализируемую функцию вокруг найденной точки и показать, что отход от оптимума ухудшает результат.
7. Прежде чем решать задачу численно, проанализируйте ее средствами символьной математики (этюд 7). Если даже аналитическое решение не будет найдено, то можно, например, выведенную частную производную использовать в численном решении системы (гибридность решения задачи – см. раздел 7.5).
[1] Он уже был раскрыт в двух предыдущих изданиях книги. Автор еще раз просит у читателя прощения за повторы и за самокомпиляцию (см. также предисловие).
[2] Рутинные операторы, формирующие матрицу M, по которой строятся графики, захлопнуты – см. рис. 2.7, где они открыты.


[3] Это и понятно: поиск корней уравнений – задача нередко существенно более сложная, чем задача поиска минимума. Поэтому чаще поступают наоборот: для решения системы уравнений составляют выражение (функционал), частные производные которого – это выражения исходной системы. У функционала ищут минимум, который одновременно является и корнем исходной системы.
[4] В среде Mathcad есть много других функций, генерирующих случайные числа с иными законами распределения.
[5] Это мы считаем, что fuzzy переводится как «пушистый», но это еще и «not in focus», то есть «нечеткий».
[6] Если, конечно, точно вычисляется значение p в пределах первых 15 цифр.
[7] Продолжим мысль А.С.Пушкина и воскликнем: «Каким образом программист в ограниченном наборе функций и команд видит будущую Программу?»
[8] Горе от ума, точнее, от высоких технологий – от цифрового, а не аналогового способа отображения реальности.
[9] В Mathcad-документе на рис. 2.2 эти вектора также формировались при построении графика. Так что перебор присутствовал и там, но был завуалирован.
[10] Здесь мы от текстового индекса отказались, чтобы читатель не путал его с числовым индексом и чтобы не получались трехэтажные индексы.
[11] Слово «враждебное» здесь не совсем точно передает суть проблемы, но читатель понимает, о чем идет речь. Так учитель подсовывает ученику заковыристый интеграл, любя его (и интеграл и ученика) и понимая, что с подобным интегралом ученик, слава Богу, никогда не столкнется, решая реальную задачу.
[12] Проблеме качественной подготовки персонала в энергетике стали уделять особое внимание после Чернобыльской катастрофы.
[13] Известный русский адвокат Лохвицкий (отец писательницы Тэффи) помог советом одной даме выпутаться из весьма затруднительных обстоятельств.
– Не знаю, как Вас благодарить! – воскликнула эта дама, встретив адвоката через некоторое время.
– Сударыня, – сказал Лохвицкий, – с тех пор, как финикийцы изобрели деньги, этот вопрос отпал сам собой.
[14] Бартер покоится на трех китах: а) неумение производственников работать в новых условиях, б) желание


уйти от налогов и в) процветание
фирм-паразитов (посредников), имеющих на реализации бартерных операций существенный «навар». Кроме того, денежный обмен убивает инфляция. В товарной цепочке все дорожает более-менее одинаково.
[15] Белая эмаль ПФ-115, если это кого-то интересует.
[16] Без этого, на первый взгляд лишнего ограничения могут получиться довольно казусные решения типа «купи на стороне маленькие банки с краской, сдай их на завод, а вместо них получи дополнительные большие – лимит отпущенных денег не будет превышен, но объем краски увеличится».
[17] Мне всегда в таких ситуациях вспоминается строка Франсуа Вийона: «От жажды умираю над ручьем...»
[18] Новая оптимизационная задача линейного программирования, которая передо мной, слава Богу (или увы – новый этюд в книгу), не стояла: Котовская ТЭЦ выделила пятитонный ЗИЛ.
[19] Исключение из правил – учебный процесс: вспомним суворовское «Тяжело в ученье – легко в бою».
[20] 16×63 = 1008, но счет барабанов у нас начинается не с единиц, а с нулей. Числа 16 и 63 легко найти на калькуляторе, разделив 14 миллионов на стоимость литра краски, перемноженной на емкость барабана – 55 и 15 литров.
[21] Автор в свою очередь немножко обманывает читателя: не присочинишь, не напишешь книгу. На самом деле все оказалось проще, а Оля по-своему была умнее всех нас: она отнесла 186 тысяч в графу «Коммерческие услуги» – и никакой оптимизации.
[22] Такой вариант расфасовки (чертова дюжина в квадрате) страшновато было везти из Котовска в Москву.
[23] Две целевые функции (объем и стоимость) в задаче о краске можно объединить в одну, перемножив или сложив их.
[24] Ломает линейность задачи такой распространенный прием, как скидка оптовикам – цена единицы товара падает при увеличении объема его закупки.
[25] Эта главка написана совместно с В.Усенко.
[26] Здесь спокойно можно обойтись без if: с логическим умножением все ясно; логическое сложение будет давать либо нуль, либо число, отличное от нуля.
[27] Текстовый процессор Word, в среде которого писалась книга, заметил ошибку в этом предложении и, либеральничая, выдал сообщение: «возможно, не хватает запятой после слова «нельзя».
[28] В среде Mathcad 8 все переменные имеют тип Variant (стандарт технологии OLE 2).
[29] Вариант названия этой главки книги: «Mathcad и «цветная» булева алгебра».
[30] Терпимость, отказ от крайних оценок и суждений.
[31] Их раскаты продолжают звучать в Северной Ирландии, на Балканах, на Кавказе, заглушая истинные причины конфликтов (см. дивертисмент № 1).
[32] Комплексная переменная позволяет перевести вопрос с отрезка на прямой (дилемма: виновен – невиновен) на плоскость (трилемма: виновен – невиновен – а было ли вообще преступление).
[33] Писатель с трагической судьбой, умевший как никто другой облекать самые глубокие мысли в самые «нелепые» литературные формы.
[34] Оружие делает равными хлипкого интеллигента, кующего славу и богатство Родины, и «качка», делающего страну пугалом для всего цивилизованного мира.
[35] См. рис. 2.6 в этюде 2– прим. автора.

A police aspect of the problem

There are always articles in the Russian press about the routine dispersal of pirate CD-ROMs of popular computer programs, by traders in Moscow outside the OMON (civilian police headquarters); somewhere at the All-Russian Exhibition Centre (formerly the NKVD building); in the Mitino district; and near the Gorbunov Palace of Culture (a favourite location called "Gorbushka").
One's first reaction is: "At last!" But later, other ideas surface. When people with machine guns at the ready are examining a hawker's documents in a pedestrian subway, nine out of ten passers-by assume not that they're enforcing law and order, but collecting a cut to turn a blind eye. The tenth passer-by believes that the small fry will be hauled in again, while the real organisers of illegal trade will get off with a mild scare. God forbid the idea that any problem can be solved purely by police action in our country! It has not proved a workable approach so far, and even when it appeared so, historically it led us down the path of the Gulag labour camps. Furthermore, the possibility is always looming.

Заяц

Чтобы приготовить рагу из зайца, нужно иметь как минимум зайца. Чтобы обработать (сгладить, аппроксимировать, интерполировать, экстраполировать и т.д.) экспериментальные данные, нужно иметь как минимум эти данные.
Чаще всего экспериментальные данные представляют собой набор пар чисел (Xi, Yi), где Yi – экспериментальные значения некоторой искомой функции, а Xi – значения аргумента.

Сортировка

Пары экспериментальных данных перед дальнейшей обработкой желательно отсортировать по возрастанию значений X. Это можно сделать вручную, переставив местами две первых пары, как в нашем случае (пункт 1 рис. 4.1), или (при объемных массивах данных) автоматически через функцию csort (пункт 2 рис. 4.2), возвращающую упорядоченную матрицу по отмеченному номеру столбца (у нас это нуль[4]
– второй аргумент функции csort). Для этого оба вектора-столбца X и Y сливаются в матрицу M с двумя столбцами, которая после сортировки расчленяется на те же, но уже упорядоченные векторы-столбцы. Это приходится делать из-за того, что некоторые функции Mathcad (например, linfit, о которой речь пойдет ниже) отказываются иметь дело с неотсортированным вектором. Да и вообще, как говорят немцы, Die Ordnung muß sein! – Должен быть порядок!

Поп-стат, или Линейная интерполяция

Встроенные функции intercept (to intercept по-английски – отложить отрезок на линии) и slope (наклон) решают самую простую и самую распространенную задачу линейного сглаживания[5]
экспериментальных данных методом
наименьших квадратов (см. пункт 3.1).

Полином

Исследователю, обрабатывающему на компьютере свои экспериментальные точки, нет дела до всех этих методологических тонкостей. Не напороться бы на фактическую ошибку, и на том спасибо. Уже упоминавшийся KISS – принцип программирования призывает пользователя прибегать к закрытым алгоритмам только в крайних случаях. При поиске сглаживающего полинома Р-й степени при Р, равном единице (линейная задача), можно обойтись без функций intercept и slope, вспомнив, что эта оптимизационная задача сводится к решению системы двух линейных алгебраических уравнений. Полином более высокой степени потребует решения более объемной, но все той же линейной системы.

Полусвобода

Потребность в замене сомножителей Xk полинома более сложными формулами вызвала к жизни функцию linfit (LINear FITting – линейное сглаживание).

Опять полусвобода

При обработке данных эксперимента, разбросанных «как попало», часто хочется плюнуть на критерии оптимизации и просто провести линию (кривую или, на худой конец, ломаную, состоящую из прямых отрезков) непосредственно через точки. Благо в среде Mathcad есть для этого инструментарий: средства линейной интерполяции (функция linterp – рис. 4.7) и интерполяции сплайном (interp – рис. 4.8) – линейным (lspline), параболическим (pspline) и кубическим (cspline).

Еще немного статистики

На рис. 4.10 показано, как функция lspline может сгладить уже не линией, а поверхностью
экспериментальные точки двухфакторного эксперимента с помощью двухмерной сплайн-интерполяции. У нас есть уже не вектор, а матрица M экспериментальных точек, зависящих от двух переменных эксперимента: давления пара и его температуры.

Экспертная оценка качества чего-либо[14]

Качество есть качество. Качество нельзя измерить[15], но можно оценить. Существуют две формы оценки качества: лингвистическая и количественная. В первом случае качество определяют словами: например, «качество высокое», «среднее», «низкое» и т.д. Во втором случае качество оценивают по некоторой условной шкале числом K (0 ? K ? M, где M - высший балл в числовой оценке качества). Например, «пять», как в российской, или 100 как в английской школах.
Для оценки качества привлекаются эксперты. Экспертной оценке качества могут быть подвергнуты товары и услуги, проекты и законы, знания и квалификация, выступления фигуристов, гимнастов или вокалистов и многое другое.
В повседневной жизни при принятии решения можно исходить из лингвистической оценки качества: мы покупаем хороший чай или инструмент высокого качества
(если позволяют средства). Однако есть такие задачи, в решении которых лучше руководствоваться количественной оценкой качества. Кроме того, обычно лингвистические оценки строятся на основе экспертных количественных оценок. Так, качество выпускника английского университета и достоинство диплома, который он получает, определяется по следующей шкале:

Средний балл в интервале оценок по 100-бальной шкале		Достоинство диплома (лингвистическая оценка)
90 - 100		С отличием
85 - 90		Первой ступени А
80 - 85		Первой ступени Б
70 - 80		Второй ступени
менее 70		Обычный

Независимо от объекта, качество которого подлежит экспертной оценке, методика ее получения в основе своей одинакова.
Рассмотрим задачу оценки деловых качеств руководителя (менеджера). Для оценки потребуются модель качества менеджера, эксперты и математическая обработка результатов работы экспертов.
Модель качества специалиста может быть представлена в виде некоторого набора важнейших качественных параметров (качеств), характеризующих его профессиональный уровень, личностные, деловые качества и предопределяющих успешную работу в рассматриваемой сфере деятельности.

Допустим, что этот набор включает следующие качества:
1) уровень и качество образования, опыт практической работы,
2) эрудиция, знания и умения в своей и смежных сферах деятельности,
3) обучаемость и способность обучать,
4) культурный уровень, моральные стандарты,
5) физическое и психологическое здоровье, возраст,
6) характер, отношение к окружающим,
7) умение руководить,
8) амбициозность, стремление к лидерству,
9) способность к риску,
10) динамизм (способность оценивать и принимать изменения внутренней и    внешней среды).
Эксперты располагают данными (анкеты, опросные листы, результаты тестов и прочее), позволяющими оценить по пятибалльной системе степень принадлежности качества кандидату. Пятибалльная система привычна и обеспечивает возможность представительной оценки степени принадлежности качества кандидату, например, по следующему алгоритму:

Принадлежность качества кандидату	Оценка в баллах
отсутствует	1
проявляется в слабой степени	2
проявляется	3
проявляется явно	4
присуще в полной мере	5

Результатом работы экспертов станет таблица оценок каждого из десяти качеств модели каждым экспертом[16]
(количество экспертов определяется важностью решения и средствами, выделенными  на экспертизу).

A moral aspect of the problem

Police raids on the black-market software dealers – and this was mentioned in the mass media – were initiated by Russian computer companies, who had noticed illegal copies of their software on hawkers' stands. It's worth noting that the office workers of these companies have cut their teeth professionally on pirate copies of others' programs. They have, of course, been installing these illegal programs with the aim of general education and science, but consider the following. It's alleged that the Moscow department of a certain renowned computer company was behind the police raids. A department of that very company followed up with a lengthy series of copyright infringement trials. This renowned company would be advised to understand the Windows interface copyright before going off to inform on someone else. Have you ever seen the principal of this firm? Does he look like a man who has been robbed?
The Biblical story tells that Jesus Christ rescued an unfaithful wife from mob law, having appealed for someone without sin to cast the first stone at the miserable woman. I have a similar feeling, that our press (the voice of the crowd) attempts to invoke mob law against our miserable domestic program users[5]. In doing so, a hawker from Gorbushka and a high school teacher are quite often lumped into the same category.[6] Yes, they both indeed have illegal copies in their hands, but they should be named and, especially, judged in a different manner, considering all the above angles. The Gorbushka traders are not concerned with copyright law at all. They should be prosecuted under quite different measures and articles of law – such as infringement of trade regulations, or even larceny and robbery. The Russian software manufacturers – and not only Russian – have got into a vicious circle. On the one hand, it's valid to protect your own rights by all possible means, but on the other, you can scarcely claim the moral high ground if you have repeatedly infringed someone else's rights and will continue to do so (if your son, for instance, 'skims' virtual games from black-market disks at home).

If the program is stolen ... No, we won't hurl a stone; we'll rephrase. If the author or the copyright owner is ignorant of the program duplication, it is not a cause for concern: conversely, it should be a matter for pride that it is used (for the author, of course, rather than the dealer). The program ought to be protected by active positive means (good after-sale service[7], or an electronic key as a last resort) rather than fiscal. There's an analogy to adultery, which is piracy in family life[8]. If a man has a pretty wife, and his neighbour is leering (or worse) at her, it is wise for him to struggle against infidelities actively by gifts and declarations – in short, good after-marriage service (we can consider the ancient chastity belt analogous to the electronic key[9]). What's unhelpful is shadowing her by private detective. And it's extremely repugnant to try to enforce community fidelity by condemning other people's wives or trying to bind behaviour by Zalesskian[10] legal declarations and clauses.
It appears the author has found for himself one solution to the computer piracy problem. It's impossible to be, as the old joke goes, "a little bit pregnant". But, probably, it's possible to be "a little bit honest" in the commercial use of others' programs. My colleagues and I design programs for power stations. This work began, naturally, with illegal use of such programs as Turbo Pascal, Visual Basic etc. But as soon as we had received the first money for our own programs we sold, we didn't pay anyone's salary or buy a new computer: we had spent it on acquiring legally the software tools we had used, even if we didn't use them any more[11]. At present all our commercial projects are based on the legal programs, while the educational ones – I work in the Moscow Power Engineering Institute – for the time being aren't. More correctly, they aren't entirely: the software is bought (though not always – a stone can be hurled at us for that) for one computer, but afterwards installed on all the equipment in an educational class[12]. But the solution of this problem is only a matter of time. Russia will either finally get bogged down in different crises, or will adjust to a normal educational system (and public health service, social maintenance etc.) with appropriate financing. For the present, it would be pragmatic not to place a moratorium on the use of illegal copies, nor condemn those who apply them to general education and school aims (considering that the range of commercial use of others' programs is very wide). At one end of the scale is the post-graduate student processing experimental data, and at the other the supplier and distributor of black-market laser disks. It's hardly the nastiest of black-market dealings: let's be pleased that the trade is in hardware and programs, rather than firearms and drugs.


Chekhov, by his own confession, " squeezed out the serf from himself drop by drop". But he never had it in mind to forcibly squeeze the bad qualities from his readers. Chekhov just helped them become better through his works, and nothing more. Let's squeeze computer piracy from ourselves, drop by drop. This process should go on without hysterics, without police swoops and especially without informing, while remaining comfortable with our own conscience and casting only occasional glances at our purses and the Criminal Code.
I fear that the computer piracy problem in our country will be settled in a purely Soviet manner: through the further expansion of the administrative machinery. A computer police would be established, for instance, which in much the same manner as the tax police wouldn't be able to poke its nose into the opulent private residences, springing up all over near Moscow without any tax returns; or into the wholesale markets that service half of Moscow without any cash registers. Harassing the ordinary business person or worker, hardly surviving in our tax disorder, is what this police would do. The tax police should break in not only bootleggers' doors, but also the luxurious office of the authority, decorated on budget means (in the first case an armoured vest should be put on; in the second, napkins). So, I am afraid that the computer police, if it is nevertheless established, won't go first to Gorbushka, but to any high school or a research institute in order to impose a fine on the above-mentioned post-graduate student.
I will spend a part of royalties for this book on a legal version of the text editor which has helped it to be written. But I want to be completely frank with the reader and say that I will only do this: if royalties suffice; if no new version of the text editor appears (in which case the new one will be purchased – or "stolen"); and if I don't change my mind.
[1] As this book was being perfected, there appeared on sale a 'black' laser disk "Mathcad 8 Pro with Russian language specification". But it was a double trick: a) the disk, naturally, contained a stolen copy of Mathcad; and b) the specification turned out to be scanned or stolen from the published paperback of VP Diakonov's Mathcad 7 manual.


1 [2]There's a saying that the piano is very easily played: all you do is push the right keys at the right time! We have already emphasised this in Etude 3, discussing computer arts. And there are only a few geniuses at the piano, because the Creator is unable to attend to all players. We won't consider here the diligence of the musician (or programmer), and refer the reader to Pushkin's "Mozart and Salieri", which develops this subject rather profoundly.
[3] In English, there is no confusion between "rights of the author" and "copyright" – a right to copy. But in Russian, "copyright" is translated ambiguously as "authorial rights".
[4] Not losses but profits may arise here. An author, having written a new work, can often make much more profit if his illegal copies are no less famous than legal ones. Examples are Bulgakov, Vysotsky, Pasternak, and Brodsky; the latter two would scarcely have obtained a Nobel Prize if they had been widely published in due time.
[5] You can bet your life that those writing accusatory articles have at least one illegal program (DOS or Windows Word, or DOS Lexicon) installed on their computer. Many police departments are equipped with computers (documentation, databases and such like) but again anything may be staked that no department, including that organising the computer market raids, cares always to purchase the legal program versions. Police officials often give crime reports on television. Next to the spokesperson, as a rule, there's a computer: they're not fools. The screen shows the two blue logos of Norton Commander - stolen, by the way.
[6] There's a poster hanging in the Белый Ветер (Byeliya Vyetyer, meaning "White Wind") computer store on Nikolskaya Street in Moscow: a tattooed hand covering a mouse, with the caption above: "Don't steal!". I have walked through the store observing the prices of notebooks, the shop's speciality. If the mark-up accounts for 20-30%, it's called commercial; if 200-300%, gangsterism. The price of the most expensive Western notebook amounts to $2500 dollars. Only a special order for mother-of-pearl keys may cost more. To afford a 5000 "bucks" notebook and its entire software is only within the grasp of the very hand drawn on the poster, whose significance is somewhat different after a trip around the store.


[7] The above- mentioned Moscow department of the renowned company on the one hand is struggling with piracy, and on the other, indirectly promoting it. A certain colleague of the author bought there, for a firm he 'moonlights' for, a legal copy of the office system for $2500, though it costs 90 roubles on a hawker's stand. During the installation, advice was needed. He phoned the dealer, who replied that the after-sales service had been reassigned to another firm. He phoned there, where they said that consultations were chargeable: $60 a question. For such money they, of course, are consulting everybody, not only legal users.
[8] A sexual angle on the problem, if you like.
[9] An analogy here is in that two parties are involved: a wife and a husband (a program and a user). And the real pirates do not care a straw: it's quite easy to break both a chastity belt and an electronic key. There is another parallel: promiscuous sex and illegal program duplication are the main ways for viruses, human and computer respectively, to proliferate.
[10]Pereslavl-Zalessky is a university city in the Rostov area, home of the Program Systems Institute, where a group of programmers wrote a declaration not to use unlicensed programs.
[11] See the chapter "How the author sold programs" in Etude 3.
[12] I became acquainted with this approach while studying (good and bad) in Germany. Quite often only one program is installed on many computers there, but at the same time they ask the permission of the manufacturing firm. The firm gives permission, sufficient for the university's needs (would they find another place so suitable for the successful advertising of its products?) realising that if it refuses, the program will be installed anyway.

Эпидемия

Одно из основных потребительских качеств компьютера – это отношение цены к производительности. С подобным критерием можно подойти и к примерам, входящим в пакеты программ. Только вместо производительности нужно рассматривать занимательность задачи, а вместо цены – размер соответствующего файла. В этом смысле рекордсмен пакета Mathcad– задача «Эпидемия». Ее уникальность еще и в том, что она – единственная, автор которой (John Truxal) отмечен в разделе Acknowledgments документации пакета Mathcad.
Суть задачи. В городе, население которого составляет 20 000 человек (см. пункт 1 на рис. 5.1), появляются 50 инфекционных больных, что вызывает эпидемию. Предположим, что прирост больных за день пропорционален произведению числа здоровых (еще не переболевших и не приобретших иммунитет) на число больных. Коэффициент пропорциональности Пр интегрирует разного рода меры профилактики. Если, к примеру, жители города будут носить марлевые повязки или сделают прививки, то этот коэффициент уменьшится. Спрашивается, как развивается эпидемия: как изо дня в день меняется число больных.

Диффуры

Описанная задача об эпидемии сводится к решению задачи Коши для системы двух обыкновенных дифференциальных уравнений (ОДУ) первого порядка относительно двух неизвестных функций Больные(t) и Здоровые(t).
Больные’(t) = Больные(t) × (Пр × Здоровые(t)-1)
Здоровые(t) = -Пр × Больные(t) × Здоровые(t)
В пункте 2 на рис. 5.1, по сути, реализован метод Эйлера[3] с единичным шагом интегрирования Dt.
Больные(t+1)
= Больныеt + Dt × Больные¢t
Здоровые(t+1)
= Здоровыеt + Dt × Здоровые¢t
Заглядывая вперед, в этюд 6 (вернее, готовя читателя к нему), покажем, как вектор-выражение пункта 2 на рис. 5.1 реализуется средствами программирования (цикл с параметром):
for t Î 1..13

Больныеt+1 ¬ Пр×Здоровыеt ×Больныеt
3доровыеt+1 ¬ 3доровыеt - Пр×Здоровыеt ×Больныеt

В среде Mathcad до версий PLUS 5.0 дифференциальные уравнения без особых ухищрений можно было решать только методом Эйлера, который имеет низкую точность и производительность (плата за простоту). Инструментарий для решения дифференциальных уравнений (систем) различного порядка и различными методами появился в арсенале Mathcad PLUS 6.0. В него входят 13 встроенных функций (Bustoer, bustoer, bvalfit, multigird, relax, Rkadapt, rkadapt, rkfixed, sbval, Stiffb, stiffb, Stiffr и stiffr), работа одной из которых (rkfixed – метод Рунге ¾ Кутты (rk) четвертого порядка с фиксированным (fixed) шагом интегрирования) показана на рис. 5.2. У этой функции пять аргументов: вектор начальных значений искомых решений, абсцисса начальной точки интегрирования, абсцисса конечной точки интегрирования, число шагов интегрирования и функция-вектор правых частей системы. Функция rkfixed возвращает в матрицу (у нас она имеет имя Z) с P+1 столбцами и n строками (P – количество уравнений или порядок уравнения) таблицу решений системы: первый (вернее, нулевой) столбец – это значения аргумента t (их задает пользователь через величины tнач, tкон[4] и n), а последующие столбцы – значения ординат решения.

Еще одна «эпидемия»

А теперь наши читатели получат домашнее задание.
Даны математическая модель развития финансовой пирамиды и ее реализация по разностной схеме. Необходимо составить и решить систему дифференциальных уравнений, описывающих развитие эпидемии, пардон, финансовой пирамиды.
К задачам, решаемым на персональном компьютере, не в последнюю очередь относятся и финансовые, связанные с ведением бюджета семьи, фирмы, завода и т.д. Итак, финансы. Компьютер может помочь учитывать, сохранять и приумножать их минимум тремя способами:
1.  На компьютере заводится электронная версия бухгалтерской книги, куда записываются все доходы и расходы. Для этих целей годятся такие программы, как Excel, Lotus 1-2-3, QuattroPro (электронные таблицы), 1C:Бухгалтерия (специализированные пакеты[9]) и т.д. Пакет Mathcad, кстати, ведет свою родословную от электронных таблиц, которые также можно считать «волшебной» счетной доской. Первое его отличие состоит в том, что в среде электронных таблиц знак «равно» ставится перед выражением, а в среде Mathcad – после. Второе отличие в том, что Mathcad поддерживает графический режим интерфейса: = 5×25 + 3Ù12 (Excel); 5×25 + 312 = (Mathcad). Третье отличие, максимально приближающее стиль Mathcad к стилю написания формул на обычном листе бумаги, заключается в том, что формулы и константы электронных таблиц жестко привязаны к сетке столбцов и строк. Об этом мы подробно поговорим в приложении 7, когда будем описывать методику совместной работы Mathcad и Excel.
2.  Компьютер подсоединяется к банковской электронной сети так, что домашняя хозяйка или бухгалтер фирмы могут сами проводить необходимые платежи, не выходя из дома. Здесь на первый план выступает проблема безопасности: платежное поручение должно быть зашифровано и сопровождаться электронной подписью. Об этом мы еще поговорим в этюде 7.
3.  На компьютере можно смоделировать и просчитать ту или иную финансовую операцию (покупка облигаций или акций, открытие счета или взятие кредита в банке и т. д.) и посмотреть, во что это выльется.

Среди примеров, входящих в пакет электронных таблиц Excel, есть задача, связанная с покупкой ценных бумаг. Рассчитывается, сколько и каких акций нужно купить, имея в запасе ограниченное количество свободных денег, чтобы сумма будущих дивидендов была максимальной (задача линейного программирования – см. рис. 2.9 и 2.10 в этюде 2, 3.10 и 3.11 в этюде 3).
Среди примеров, входящих в пакет математической программы Mathcad, есть задача, связанная с моделированием развития эпидемии. Задается начальное число здоровых и больных, а далее просчитывается, как развивается эпидемия – как меняется число больных по дням. Мы только что эту задачу разобрали.
Попробуем скрестить эти две задачи и получить новую, связанную с моделированием развития финансовой пирамиды, которая во многом похожа на эпидемию. Сделаем мы это в среде пакета Mathcad, который вполне подходит для таких целей. Более того, к пакету Mathcad можно прикупить электронный учебник «Personal Finance», который поможет научиться вести финансы и из которого при необходимости в рабочий документ переносятся нужные формулы и константы.
Автор имел опыт участия в финансовых пирамидах. Первый опыт ¾ очень давний, очень невинный и без особых последствий. В школьные годы кем-то в классе было предложено не тратить выдаваемые родителями ежедневные обеденные 20 копеек, а складывать их и отдавать все разом поочередно каждому участнику этой финансовой кампании. Так воплощалась старая, как мир, детская мечта: «Вот если бы каждый взрослый дал мне по копеечке... Он бы этого и не заметил, а у меня бы оказался целый капитал». Но в классе вышло так, что участники этой складчины, получившие деньги, из игры выбывали, она потихоньку глохла и кто-то (а среди них оказался и автор) остался с носом.
Второй опыт участия в финансовых пирамидах автор приобрел вместе со всей страной 17 августа 1998 года.
Сейчас, слыша о крахе «Тибетов», «Светлан» и прочих «Чар», автор вспоминает детскую мечту, школьные двугривенные и не только их.
Банковская система любой страны, как на трех китах, покоится на трех числах. Первое число N1 – плата за кредит. Взял в банке сто рублей – будь любезен в конце года верни 100 + N1 рублей. Второе число N2 – процент по вкладу. Положил в банк сто рублей – получи в конце года 100 + N2 рублей. Разница между первым и вторым числами (N1 > N2) заставляет банки прибыльно работать. Третье число N3, подпирающее снизу два первых и заставляющее людей нести деньги в банк, – это величина инфляции[10]. В нормальной экономической ситуации низкий уровень инфляции и не очень высокая плата за кредит держат в узких рамках процент по вкладу:
N1 > N2 > N3.
Если же инфляция составляет 1000 и более процентов в год, то многие люди, забывая о ненормальности такой ситуации, легко верят в 1000 и более процентов годовых по вкладу (ведь величина N2 должна быть больше величины N3) и «ложатся в основание» очередной финансовой пирамиды. Если, конечно, законодательством страны позволительно такие пирамиды строить. Есть и менее наивные люди, понимающие, что пирамида – это особый род игры, где нужно уметь «вовремя смыться».
Итак, строим финансовую пирамиду.

Немного истории

При работе в среде Mathcad всегда ощущалась потребность в программировании для расширения и совершенствования базового набора математических инструментов – операторов и функций. Искушенные пользователи решали эту проблему тремя путями.
Путь 1. В самых первых версиях Mathcad были[2] две функции (if и until), позволявшие через различные хитрости и трюки реализовывать две основные алгоритмические конструкции – выбор (if) и повторение (until). Хитрить же приходилось из-за неспособности функций if и until иметь в качестве аргументов блок составных операторов. Поэтому для реализации даже несложного алгоритма нужно было подключать механизм вложенных функций и
операторов, что нередко превращало программу
в настоящую криптограмму, в которой даже сам автор разбирался с трудом.
Вот как выглядит поиск корня уравнения методом половинного деления (рис. 6.1) с использованием функции if и until (автор А.Шевченко). Читатель, забегая вперед, может сравнить «программу» на рис. 6.1 с программой (без кавычек) на рис. 6.20, реализующей практически тот же алгоритм.

A and B sat on a pipe

We can imagine A and B sitting down to pass the time of day – in our case, not on a simple pipe, but on a fire bucket. We'll now explain the 'universal' meaning of these parametrical factors A and B (more correctly A_r, B_r, A_h, B_h, A_v and B_v) included in the approximation expressions of stages 2, 5 and 8 (fig. 6.41-43).
Viewing the fuzzy set as a statistical distribution, A represents the 'spread' of the distribution, and B the parameter value giving the peak of the distribution. Imagine we carry out a global statistical experiment. We measure for all adult humans some parameter – weight, height, intelligence, etc – whether represented numerically or estimated by some criterion (genius, talented, very clever, simply clever... down to idiot). The data points we shall transform into a curve (see sections 1-3 in figures 6.41, 6.42
and 6.43) where the X-axis is the measured human parameter, and the Y-axis the percentage of people with a given value of that parameter. We carry out this statistical exercise separately for men (M) and women (F). What do we get?
Case 1: AM = AF, but BM > BF:

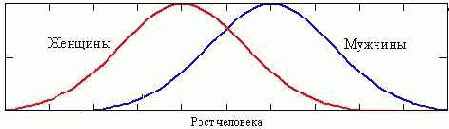
Curves turn out like this for parameters – such as height, weight, strength of muscles, etc – pertaining particularly to men rather than women. This is related to evolution: sexual dimorphism is related to the general trend in species size. If the male body is larger than the female, the next generation tends to be larger. With spiders, for example, the male is much smaller than the female, and so – thank God – spiders are smaller now than the geological past.
Case 2: AM < AF, but BM = BF:

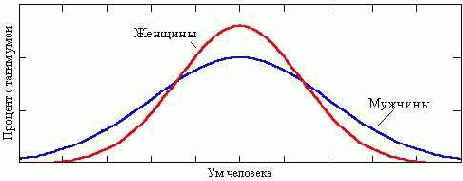
The curve looks like this for a parameter – intelligence – whose importance applies equally to both sexes, and has not varied for millennia. Many consider it quite proven, that if modern humans were suddenly stripped of education and culture, we would be no more intelligent (maybe even less so) than the Ancient Greeks. It's not known why, but there is a greater spread for men: there are more men of genius (Nobel prizewinners, inventors, writers and artists – at the right edge of the diagram) only because there are also more men of extremely subnormal intelligence (the left edge). The average woman is cleverer the average man: the centre of the "female" distribution is raised at the expense of a smaller spread. The areas of both curves is, however, identical: no offence intended to anyone, but we believe that the Lord God or Nature (whichever you believe in) has shown consideration in distributing intelligence equally to both halves of humanity.
We can try to apply the theory of fuzzy sets, as described in Etude 3, to the problem of computer piracy. The law divides all people into two precise sets: {legal users of programs} and {illegal users – pirates}. In real life, it's much more complex: computer users fall into two fuzzy sets, with a great variety of motives. At one extreme are people trading 'black' disks at Gorbushka (the left-hand axis of the diagram above); at the other are those who work only with legal copies and have never broken any license agreement (the right-hand axis). Again, it's possible to construct a humpbacked statistical curve, this time above an axis "sinner ... saint" describing the condition of the computer market in a particular country. Where does the maximum of this curve lie, and how is it shifting with time?

A и B сидели на трубе

Сидели они не на простой трубе, а на пожарной, точнее – на пожарном ведре: сейчас будет рассказано об «общечеловеческом» смысле параметрических коэффициентов A и B (вернее Ar, Br, Ah, Bh, Av и Bv), входящих в аппроксимирующие выражения пунктов 2, 5 и 8 (рис. 6.41-43).
Давайте проведем глобальный статистический эксперимент – у всех взрослых людей на земле измерим какой-либо параметр: вес, рост, ум и т.д. ¾ словом все то, что можно измерить числом или оценить критерием (гений, талант, очень умный, просто умный... совсем дурак).
Полученные точки превратим в кривые (см. пункты 1-3 на рис. 6.41-43), где по оси X отложим параметр человека, а по оси Y – процент людей с данным параметром. При этом статобработку проведем отдельно для мужчин (м) и женщин (ж). Что мы получим?
Случай 1: Ам
= Аж, но Вм > Вж:

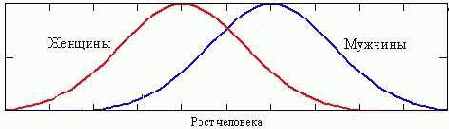
Такие кривые получаются для тех параметров, значение которых у мужчин больше, чем у женщин (рост, вес, сила мышц и т.д.). Это связано с эволюцией – если мужская особь крупнее женской, то новые поколения укрупняются. У пауков, например, самцы намного меньше самок – пауки сейчас, слава Богу, более мелкие, чем в доисторические времена.
Случай 2: Ам
< Аж, но Вм = Вж:

А так будут выглядеть кривые для параметров, значения которых у человека за последние несколько тысяч лет не менялись – ум, например. Многие вполне обоснованно полагают, что современный человек, если убрать налет образованности и культуры, ненамного умней древнего грека. Среди мужчин гениев[66]
(нобелевских и прочих лауреатов, великих изобретателей, писателей[67]
и художников – см. правый край графика) больше лишь потому, что и дураков среди мужчин достаточно (левый край графика). Но средняя женщина умнее среднего мужчины – центр «женской» кривой приподнят за счет меньшего разброса по краям: площади фигур под графиками одинаковы – никого не обижая, будем считать, что Господь Бог или Природа (кто как для себя считает) одинаково наделили умом обе половины человечества.
Теорию нечетких множеств, как уже было отмечено в этюде 3, можно попытаться приложить и к проблеме компьютерного пиратства. Закон делит всех людей на два четких множества: «множество легальных пользователей программ» и «множество нелегальных пользователей (пиратов)». В реальной жизни все намного сложней: нечетких множеств людей, причастных к компьютерам, великое множество (извините за тавтологию). Есть множество торгующих на «Горбушке» «черными» дисками (левый край оси – см. графики выше) и есть множество тех, кто принципиально работает только с легальными копиями и никогда не подаст руки согрешившим – нарушившим какое-либо лицензионное соглашение (правый край оси). Можно опять же над осью «грешник-праведник» построить горбатые статистические кривые, описывающие состояние компьютерного рынка в конкретной стране. Где находится максимум этой кривой, куда и с какой скоростью он перемещается во времени?

Философско-религиозный аспект проблемы

Естествоиспытатель, желающий познать окружающий мир, не может прямо обратиться к Создателю
– к Богу или к Природе, кто как для себя считает, а должен задавать вопросы самому объекту исследования, то есть должен проводить эксперимент – вносить в объект возмущения и фиксировать реакцию на них.
У программы есть авторы. Их имена далеко не всегда указаны на коробках, дисках и в документации, но они есть. Следовательно, какие-либо эксперименты над программами излишни. Возникающие вопросы нужно адресовать либо документации, либо самим авторам. Но! Если пользователю, к примеру, потребуется уточнить, в градусах или в радианах измеряется аргумент синуса, то он не будет рыться в документации, а просто напишет x:=sin(90) и посмотрит, чему окажется равна переменная x. Подобные эксперименты пользователи ставят ежечасно, обращаясь к документации только в особо сложных случаях и, как правило, не находя там ответа. Обращение же к Создателю проблематично. На hot-line сидят не авторы, а продавцы программ, что, как понимает читатель, далеко не одно и то же. Консультант фирмы скорее всего попросит вас перезвонить через пару дней, за которые он проведет свой эксперимент над программой и попытается найти ответ. Да и обращение к самому автору часто ничего не дает, так как он уже забыл свое детище и всецело поглощен новым проектом. Если даже это не так, то автор может и не помнить всех свойств, а уж тем более нюансов своего творения.
Из-за этого при работе с программами пользователь часто забывает, что это продукт ума и рук человеческих (Природа сотворенная), полагая (на уровне эмоций), что это плод работы анонимного и недоступного Создателя (Природа творящая), у которого нет hot-line. Здесь, по-видимому, и кроется философское объяснение
(но ни в коем случае не оправдание) широкого распространения нелегального копирования программ. Имеются в виду не китайско-болгарские компакт-диски типа «Все для офиса» – воровство есть воровство[68]. Речь идет об относительно честных людях, ставящих на свой компьютер программу с того же лазерного диска, чтобы познать Природу и передать свои знания, например, студентам.

Можно считать, что Создатель, бросив сверху яблоко и угодив им по Ньютоновой голове, приоткрыл нам одну из тайн своего Божественного Замысла. Заслуга гения (Ньютона) – в умении оказаться в нужном месте в нужное время[69]. Программы (и не только гениальные) как бы тоже падают к нам сверху, и человек не обязан за них платить сумасшедшие по российским меркам деньги. Отсюда и живучесть идеи shareware, которой противятся в первую очередь продавцы, а не авторы программ.
Как говорится, есть мнение, что Бог создал по своему образу и подобию не только человека, но и компьютер. Написание для него программы – это вдыхание души в безжизненное нагромождение железок. Торговля телом (трансплантация органов, переливание крови или, наконец, проституция) – реалии наших дней. Покупка и продажа души встречается только в сказках и художественной литературе (история Фауста, например). Приобретая программный продукт, мы опять же покупаем только «тело» – диски, документацию, информацию и скидки по новым версиям, а главное – послепродажный сервис.

Общекультурный аспект проблемы

Откройте первую страницу любого западного издания и вы увидите предупреждение о том, что эту книгу (ее отдельные главы или страницы) запрещено копировать. Автор сначала написал «и вам бросится в глаза грозное предупреждение», но потом заменил на нейтральное «вы увидите». Все прекрасно понимают, что имеется в виду копирование в коммерческих целях. Как на Западе, так и у нас в библиотеках вполне легально стоят копировальные аппараты, на которых «ксерят» книги и журналы от корки до корки, исключая разве что ту самую страницу с грозным, а по сути пустым предупреждением. Снимать копии с печатной продукции любыми доступными способами (выпиской цитаты в тетрадку, например) можно в образовательных и научных целях. Более того, если кто-то препятствует такому способу распространения информации, то это расценивается как прямое нарушение прав автора. Не авторских прав[70], а именно «прав автора». За этой стилистикой скрывается то, что авторскими правами почти всегда распоряжается не автор, а издатель. Права же автора, это как права человека, которые «от Бога» и которые невозможно передать кому-либо. Появление на рынке «черных» копий книги расстраивает обладателя авторских прав. Автор же (обладатель прав автора) сначала радуется этому, а потом уж огорчается по поводу потери будущей и, как правило, эфемерной прибыли[71]. Размытость границы между коммерческим и некоммерческим использованием копий можно видеть и в другом. Аспирант «наксерил» чужих статей, слепил из них диссертацию (скажем мягче – часть диссертации), получил ученую степень, а через нее – высокооплачиваемое место на фирме или в университете. Даже если слово «слепил из них» заменить на «которые помогли ему написать», то суть дела не меняется: знания – это самый дорогой товар на цивилизованном рынке.
Такой подход к книжной продукции пользователи ЭВМ (а это сейчас самая читающая публика – в метро мелькает не только дамский роман, но и какой-нибудь User’s Guide или «Excel для «чайников») перенесли и на программные продукты (продукция, продукты – это все рыночные термины). Изучить программу так же интересно и полезно (в общекультурном, образовательном плане), как и книгу. Беда, а быть может, и счастье программ лишь в том, что копировать их намного проще, чем книги. Кроме того, даже самые гениальные программы, в отличие от классической литературы, умирают раньше срока завершения действия авторских прав. Пушкина или Шекспира сейчас кто угодно может издавать.

Милицейский аспект проблемы

В печати то и дело мелькают сообщения о том, что где-то на ВВЦ (бывшая ВДНХ), в Митино и у ДК им. Горбунова («Горбушка») ОМОН разогнал торговцев пиратскими CD-ROM с записями популярных программ для ЭВМ[72]. Первая реакция на это: «Наконец-то!» Но потом приходят другие мысли. Когда люди с автоматами наперевес проверяют документы у лоточников в подземном переходе, то девять прохожих из десяти думают не о том, что наводится порядок, а о том, что просто собирается дань. Десятый прохожий думает о том, что опять «заметут» всяких мелких сошек, а организаторы нелегальной торговли отделаются легким испугом. Боже упаси решать у нас какую-либо проблему чисто полицейскими мерами. До сих пор из этого ничего толкового не получалось, а если проблема и решалась, то выходил какой-то ГУЛАГ. Кроме того, здесь плавно выходит на первый план

Моральный аспект проблемы

Милицейские рейды на рынки программ, и это отмечалось в печати, были проведены по наводке сотрудников российских компьютерных фирм, увидевших на лотках незаконные копии своих программных продуктов. Сотрудников, заметим, профессионально выросших на тех же пиратских копиях, правда, чужих программ. Нелегально ставили они их на свои компьютеры, конечно, в общеобразовательных и в научных целях, но... см. выше. К милицейским рейдам, говорят, приложило руку и московское отделение одной знаменитой компьютерной фирмы. Той самой, за которой тянется длинный шлейф судебных процессов по поводу нарушения чужих авторских прав. Знаменитой фирме можно посоветовать сначала разобраться с вопросами об авторских правах на оконный интерфейс, а потом уже «стучать куда следует». Вы видели главу этой фирмы? Похож он на человека, которого обокрали?
Библейское предание говорит о том, что Христос спас неверную жену от самосуда толпы, призвав первым бросить в несчастную женщину камень того, кто сам безгрешен. У автора такое чувство, что какое-то подобие самосуда над несчастными отечественными пользователями программ пытается совершить наша пресса (глас толпы)[73]. При этом на одну доску нередко ставятся и торговец с «Горбушки», и вузовский преподаватель[74]. Да, и у того и у другого на руках нелегальные копии, но называть и, главное, судить их нужно по-разному, с учетом вышеизложенных аспектов. Торговцы с «Горбушки» вообще не имеют никакого касательства к закону об авторском праве. К ним нужно применять другие мерки и другие статьи закона – те, где говорится о нарушении правил торговли или даже о воровстве и разбое. Производители программных продуктов у нас в России (да и не только у нас) попали в какой-то заколдованный круг. С одной стороны, хочется защитить свои права всеми возможными средствами, а с другой – не имеешь на то морального права, ибо сам такие же, но чужие права неоднократно нарушал и будешь нарушать впредь – сын, например, дома скачивает с «черных» дисков игрушки.
Если программу воруют... Нет, камень бросать не будем и скажем по-другому. Если программу копируют без ведома автора или того, кому принадлежит copyright, то нужно не огорчаться, а радоваться. Автору, конечно, а не продавцу. Защищать же программу следует активными (хороший послепродажный сервис[75], электронный ключ, наконец), а не фискальными средствами. Аналогия из области адюльтера – пиратства на семейном фронте[76]. Если у вас красивая жена, то на нее засматриваются (и не только) окружающие. Бороться с изменами следует активными методами – подарки, признания, короче, хороший послесвадебный сервис, пояс верности (электронный ключ), на худой конец[77]. Слежкой тут делу не поможешь. Тем более противно, когда осуждают чужих жен, да еще пытаются при этом писать какие-то «залесские» декларации и статьи.

Автор, кажется, нашел для себя решение проблемы компьютерного пиратства. Считается, что нельзя быть немножко беременной. Но быть немножко честным в коммерческом использовании чужих программ, наверно, можно. Автор со своими коллегами разрабатывает программы для электростанций. Эта работа начиналась, естественно, с нелегального использования программ типа Turbo Pascal, Visual Basic и т.п. Но как только мы получили первые деньги за проданные программы, то пустили их не на зарплату, не на покупку нового компьютера, а на приобретение использованных инструментальных средств – даже тех, с которыми мы уже не работали[78]. Теперь у нас все коммерческие проекты базируются на легальных программах, образовательные же (автор работает в Московском энергетическом институте) – пока нет. Вернее, немножко нет: покупается (да и то не всегда – пусть в нас бросят камень) программа для одного компьютера, а устанавливается на все машины в учебном классе[79]. Но решение этой проблемы – дело времени. Россия либо окончательно увязнет в разного рода кризисах, либо наладит нормальную систему образования (здравоохранения, социального обеспечения и т. д.) с нормальным финансированием. Третьего не дано. А пока же неплохо установить мораторий не на использование нелегальных копий, а на осуждение тех, кто это делает в общеобразовательных и учебных целях, понимая при этом, что диапазон коммерческого использования чужих программ очень широк. На одном его конце аспирант, обрабатывающий экспериментальные данные на компьютере, а на другом организатор доставки и распространения «черных» лазерных дисков. Хотя это не самый страшный «черный» бизнес: радуйтесь, что торгуют «железом» и программами, а не настоящими винчестерами и наркотиками.
Чехов, по его собственному признанию, по каплям выдавливал из себя раба. Но ему даже в голову не приходила мысль попытаться насильно выдавить что-то гадкое из читателей. Чехов своими произведениями помогал им становиться лучше, только и всего. Давайте же выдавливать из себя по каплям (вычерпывать ведрами) компьютерного пирата. Делать это надо без истерик, без милицейских шмонов и тем более без стукачества, оставаясь наедине со своею совестью, поглядывая в свой кошелек и в Уголовный кодекс.


Автор боится, что проблема компьютерного пиратства у нас в стране решится чисто по-советски – через дальнейшее увеличение административного аппарата. Будет, например, создана компьютерная полиция, которая по примеру своих собратьев из налоговой полиции не сможет сунуть нос в миллиардные особняки, как грибы растущие в Подмосковье без всяких налоговых деклараций, или на оптовые рынки, отоваривающие пол-Москвы без каких-либо кассовых аппаратов. Попортить нервы предпринимателю-производственнику, еле-еле выживающему в нашем налоговом беспределе – это полиция может. Налоговая полиция должна вышибать двери не только у нелегальных бутлеггеров, но и в шикарных кабинетах начальства, отделанных на бюджетные средства. В первом случае нужно надевать бронежилет, а во втором – памперсы. Так вот, автор боится, что компьютерная полиция, если она будет создана, первым делом пойдет не на «Горбушку», а в какой-нибудь ВУЗ или НИИ, чтобы наложить штраф на вышеописанного аспиранта.
Часть полученного за книгу гонорара автор тратит на приобретение легальной версии текстового редактора, с помощью которого эта книга писалась. Но автор хочет быть с читателем откровенен до конца и сообщает, что программа будет куплена:

если на это хватит гонорара;

если не появится новая версия текстового редактора – покупать (или «воровать») придется уже ее;

если автор не передумает.

Другую часть полученного за книгу гонорара автор потратит на приз читателю, приславшему самую короткую программу перевода римского числа в арабское. Для «затравки» автор помещает в конце этюда программу перевода арабского числа в римское (см. первую половину рис 6.46).

Открытое письмо пирата в адрес компьютерных изданий (English version of text)

Открыв любой номер любого компьютерного издания, можно наткнуться на статью, касающуюся проблемы нелегального копирования и распространения программ. Данное письмо также затрагивает эту тему, но несколько в ином ключе. Здесь нет попытки кого-то осудить или оправдать. Автор просто пытается рассмотреть проблему в необычных аспектах: философском, религиозном, общекультурном, милицейском, моральном и даже... сексуальном.

Отладка Mathcad-программ

Каждый, кто когда-либо серьезно занимался программированием, знает, что написать программу можно за несколько минут. Но на поиск ошибки в ней могут уйти часы, дни, недели...
Английский эквивалент термина отладка – a debugging заслуживает отдельного разговора. A bug по-английски – жучок, а приставка de означает удаление. Сам термин debug дословно можно перевести как обезжучивание. Эта калька с английского не такая уж бессмысленная. Один из первых компьютеров стал барахлить из-за того, что в его электронных внутренностях запутался таракан, закоротил контакты, обуглился и, как некий связист-камикадзе, замкнул их, внеся тем самым изменения в электронную схему машины.
К сожалению, пакет Mathcad не оборудован штатными средствами отладки. А к ним обычно относят следующую тройку инструментов:
1. Трассировка программы (Trace), когда после ее запуска цветом или жирным выделением отмечаются выполняющиеся операторы. Так можно проверить соответствие порядка выполнения операторов задуманному алгоритму. Программу можно выполнять и пошагово – очередной оператор выполняется после нажатия программистом какой-либо оговоренной клавиши. При этом можно «заходить» или не «заходить» в функции или процедуры. Не заходят в них в тех случаях, когда они отлажены и оттестированы отдельно (заранее).
Система Mathcad, выполняя операторы документа, своеобразно трассирует их. Если какой-либо оператор выполняется достаточно долго (суммируются элементы объемного вектора, например), то он оконтуривается и штрихуется зеленым цветом. Это можно было бы назвать трассировкой, если такое выделение операторов велось бы и в теле программ с циклами и альтернативами. Но система Mathcad рассматривает программу как единый оператор (второй атрибут программирования) и не подсвечивает операторы в нем, а оконтуривает и подсвечивает всю программу: «Ждите ответа!»
2. Пошаговое выполнение операторов обычно сопровождают просмотром (Watch) текущих значений всех или некоторых переменных. При этом на дисплей выводится специальное окно, где отмечаются имена переменных, их тип, текущее значение и др.

3. Критические операторы (места) программы отмечают точками останова (BreakPoint), где компилятор прекращает выполнение машинного кода. После этого программист может просмотреть значения всех или некоторых переменных (см. выше), подправить программу и дать команду на ее дальнейшее выполнение (выполнять программу далее в нормальном режиме, пошагово или даже пустить вспять, если чувствуется, что ошибка случилась ранее отмеченного места).
Но повторяем, среда программирования Mathcad лишена каких-либо специализированных средств отладки. Объяснить и в какой-то мере оправдать это можно лишь тем, что программирование – это лишь вспомогательный инструмент при решении задач[80]. Но при отладке самой программы Mathcad, по-видимому, инструменты отладки использовались. Автор об этом узнал случайно, когда работал с самой первой бета-версией Mathcad 8, нажав правую кнопку мыши с курсором, помещенным на рабочем листе. Вот что появилось на экране дисплея (рис. 6.48): локальное меню с волшебным словом «Debugger»:

Оптимизация Mathcad-программ

Программист, написав и отладив программу, как правило, на этом не успокаивается и начинает ее улучшать – оптимизировать. Таким программистам можно посоветовать повесить на стене перед глазами такой листочек:
«За все нужно платить!»

 «Лучшее ¾ враг хорошего!»

«Не до жиру, быть бы живу!»
Далее в тексте читатель будет встречать подобные тривиальные истины, некоторые из них он может также вывешивать в виде плаката[89].
Поговорим о том, что можно улучшить в программах – хотя бы в тех, которые помещены в этой книге.
Программы можно оптимизировать по разным параметрам. Вот три основополагающих:

Время выполнения программы;

Объем программы: место, занимаемое ею в ОЗУ компьютера, длина файла с исходным текстом программы, хранимого в архивной памяти.

Читабельность программы; степень ее открытости для изучения другими людьми и для доработки самим автором или кем-то другим.

Последнее качество в отличие от двух первых не так просто выразить числом, на которое можно целенаправленно влиять. Но мы уже рассмотрели понятие удобное
пожарное ведро и знаем, как нечеткие
величины можно обрабатывать четкими методами (см. рис. 6.41-6.45). Открытость программ очень важна в среде Mathcad, так как этот пакет интенсивно используется в сфере образования. Все три параметра (и еще какие-то другие) можно объединить в один интегральный и применить к нему метод экспертных оценок с функциями принадлежности какого-либо элемента (параметра) нечеткому множеству «оптимально-неоптимально».
Все три вышеотмеченные качества взаимосвязаны. Только в очень неряшливо написанной программе все параметры можно улучшить. Обычно же бывает так, что, улучшая читабельность программы человеком, мы ухудшаем ее «читабельность» компьютером: комментарии в программе (в нашем случае – текстовые константы) не только увеличивают объем программы, но и замедляют ее прогонку.
Вот другой пример. Если в программе на рис. 4.10 (сплайн-интерполяция) исходные векторы и матрицы термодинамических параметров водяного пара переместить в файл на диске, а в программе оставить операторы его считывания (функция READ), то объем программы существенно уменьшится, но читабельность ее при этом ухудшится (самое интересное уйдет с экрана дисплея), а время ее выполнения изменится.

Mathcad не имеет специализированных средств, предназначенных для оптимизации программ. В «настоящих» языках программирования, вернее, в «настоящих» средах создания программ они есть.
Одно из них, называемое «profiler» (профайлер, профилировщик), позволяет провести некий хронометраж программы и выявить ее слабые места, нуждающееся в «укреплении» (в оптимизации).
Итак, поговорим о том, как Mathcad-программы можно оптимизировать.
1. Отлаживать
программу можно только после ее написания, но оптимизировать программу не просто можно, но и нужно еще до открытия панели инструментов программирования (см. рис. 6.2). «Нет ничего практичнее хорошей теории!» – вот еще строка, заслуживающая быть плакатом (см. выше). Эта истина заставляет программиста искать для программы оптимальный алгоритм.
Как можно найти корень алгебраического уравнения на отрезке неопределенности a-b? Во-первых, можно разбить интервал a-b на небольшие отрезки, равные TOL (предопределенная переменная Mathcad, отвечающая за точность расчетов), и зафиксировать место, где значения функции ближе всего к засечкам на оси х – см. рис. 6.54.

Панель программирования

С первого взгляда на Mathcad возникает вопрос: почему в него не был встроен какой-либо известный и широко используемый язык программирования, а разработан новый, ни на что не похожий[4]? Электронные таблицы Excel, текстовый редактор Word и базы данных Access (Microsoft Office) используют встроенный BASIC[5], что кажется естественным даже для самых непримиримых противников этого языка. Но после детального знакомства с языком Mathcad удивление сменяется пониманием и даже удовлетворением. Становится очевидным, что в рамки традиционных языков с их программами в текстовом формате невозможно втиснуть богатый набор инструментария Mathcad, который реализован не только и не столько в виде функций, сколько в общепринятом в математике виде[6].
В Mathcad, по сути, не встроен язык программирования, а просто снято вышеупомянутое ограничение на использование составных операторов в теле алгоритмических управляющих конструкций выбора (if) и повторения (until).
Кроме того, введено понятие локальной
переменной, добавлен цикл с параметром for, операторы досрочного выхода из цикла break и continue, а также оператор досрочного выхода из программы return. Алгоритмические конструкции в среде Mathcad вводятся не традиционным набором через клавиатуру ключевых слов if, then, else, while и т.д., а нажатием одной из кнопок панели программирования (Programming):

Программа-константа – программа-переменная – программа-функция

Кнопки программирования (см. рис. 6.2) по своей сути дополняют традиционные встроенные операторы (+, -, *, ¸ ...) и функции (sin, cos, log ...), с помощью которых пользователь формирует выражения, значение которых присваивается константам, переменным и функциям пользователя.

Программа-скаляр – программа-вектор – программа-матрица

Эта тройка переменных может задаваться, естественно, и программно.

Рекурсия

Рекурсивная функция – это такая функция, которая вызывает сама себя в момент ее создания[22]. Рекурсия – очень мощный и удобный инструмент решения задач. Так, например, один из самых быстрых алгоритмов сортировки массива использует рекурсию. Вычислить детерминант квадратной матрицы также помогает рекурсия и т.д.
Языки программирования в своем развитии обычно проходят три стадии:
1. Рекурсия невозможна.
2. Рекурсия не разрешена, но применяется по принципу: «Если нельзя, но очень хочется, то можно». Так, на старых версиях языка BASIC рекурсия реализовывалась через оператор ON N GOTO, передающий управление программой на N-ю строку.
3. Рекурсия разрешена.
Mathcad вторую стадию проскочил (условно проскочил – это мы еще отметим, разбирая рис. 6.13).
И вот уже трещат морозы
И серебрятся средь полей...
(Читатель ждет уж рифмы розы;
На вот, возьми ее скорей!)
Читатель ждет уж примеров рекурсии в среде Mathcad? Скорее всего, нет. Традиционные примеры (розы-морозы) ему оскомину набили. Но мы попробуем что-нибудь свеженькое. Например, двустороннюю (ретроспективную) рекурсию.
Как запомнить число e (основание натурального логарифма) с девятью цифрами после запятой? Очень просто – две целых семь десятых плюс два раза Лев Толстой – 2.718281828, то есть к числу 2.7 нужно приписать два раза год рождения классика (1828). Остается самая малость – запомнить, в каком году родился Лев Толстой, или, на худой конец, сообразить, что это случилось в прошлом веке[23], чтобы вспомнить хотя бы три знака числа e после запятой: 2.718. Ретроспектива, обращенная в XIX век, поможет запомнить довольно-таки точное значение одной из фундаментальных констант математики.
Как запомнить, что факториал нуля равен не нулю (типичная ошибка), а единице? Очень просто. Нужно применить ретроспективный метод поиска факториала числа: сообщить машине факториал какого-либо положительного числа N (5! = 120, например) и то, что факториал предыдущего числа N-1 равен факториалу первого (N!), разделенному на N. Факториал пяти (120) – это такая же тривиальная истина, как и то, что Лев Толстой родился в XIX веке, а грубая оценка числа е – 2.7.

Размерность

По знаменитой формуле Н.Вирта программа – это сумма алгоритма и структуры данных. Алгоритм программы в среде Mathcad задается нажатием десяти кнопок на панели программирования (рис. 6.2), отвечающих за циклы, альтернативы и прочее. Структура данных в среде Mathcad также проста. Там есть только вещественные переменные двойной точности, которые могут превращаться в комплексные или целочисленные, группироваться в векторы и матрицы (простые и вложенные), принимать, если надо, текстовые значения.

Remake

В седьмой части этюда автор расскажет в стиле римейк об особенностях языка Mathcad.
Почему римейк? Во-первых, см. предисловие. Во-вторых, у автора сохранился файл с текстом статьи «Turbo Pascal 7.0. Взгляд со стороны» (КомпьютерПресс, № 7’93), которая и подвергается римейку (remake – переработка). В-третьих, язык Mathcad, как и язык Pascal, оказался окутан паутиной старых догм[33]
структурного программирования, о которых писалось в упомянутой статье. Это делает римейк не только простым, но уместным и естественным.
Итак, remake.
Попробуем на простых примерах показать, что ввод в язык Mathcad операторов break, continue и return (см. выше) – только полшага в сторону повышения гибкости управляющих конструкций этого языка программирования.

Проблема метки (English version of text)

Проблему метки, вернее, проблему избавления от метки, мы рассмотрим на примере решения старинной английской задачи о рыбаках и рыбке:
«Три рыбака легли спать, не пересчитав и не поделив улова. Ночью один из рыбаков проснулся и решил уйти, забрав свою долю. Но число рыб не делилось на три. Тогда он, не долго думая, выбросил одну рыбку, а из остатка забрал треть. Второй и третий рыбак поступили аналогичным образом – ушли по-английски и по-джентельменски, выбросив по одной рыбке и оставив спящим товарищам четное число рыб. Спрашивается, какое минимальное число рыб в улове отвечает условию задачи».
Пусть читатель сначала попробует решить эту задачу без компьютера. Компьютер же мы привлечем к этой работе для двух целей. Во-первых, на задаче о рыбаках и рыбке мы рассмотрим некоторые методы структурирования
программ в среде Mathcad – методы освобождения программ от меток и «втискивания» их в узкие рамки структурных управляющих конструкций, описанных выше (см. рис. 6.2). Во-вторых, мы покажем, что задача о рыбаках и рыбке до сих пор решалась неправильно...
Эту задачу в среде Mathcad можно решить, не прибегая к средствам программирования.

Золотое сечение

Программа на рис. 6.26 ищет минимум функции одной переменной методом золотого сечения[41]. В ней используется вспомогательная функция с именем Зол_Сеч, позволяющая отрезок a-b (отрезок неопределенности) поделить в золотом соотношении. Вывод этой функции через решение уравнения золотой пропорции средствами символьной математики (см. этюд 7) представлен в пункте 1 рис. 6.26.

Силы Кориолиса

На рис. 6.27 представлена созданная с помощью программирования функция minimum, возвращающая координаты точки минимума функции многих переменных (ее имя – аргумент y) и начинающая поиск от начальной точки приближения (вектор x). Алгоритм поиска минимума прост. От точки начального приближения по всем координатам делается шаг D (третий аргумент функции minimum). В новых местах[44]
вычисляются значения минимизируемой функции. Туда, где функция имеет минимальное значение, делается переход, данная точка становится новой точкой приближения к минимуму, а все вышеописанные действия («ощупывание» функции вблизи точки приближения) повторяются. Если окажется, что вблизи новой точки приближения все новые значения функции увеличиваются, то шаг поиска (D) уменьшается вдвое, а все действия повторяются. Поиск заканчивается, когда значение D становится меньше TOL (системная переменная Mathcad, регулирующая точность вычислений).

Продолжение задачи о краске

Применение средств программирования позволяет по-новому решить нашу задачу о краске (см. рис. 3.11 в этюде 3). При единственности решений, оптимизирующих либо объем, либо стоимость краски, разливаемой в барабаны двух типов, можно найти не одно, а ряд решений, где объем меньше максимального не более, чем на 2%, а при поиске максимума цены – на 0.5%.

Задача о компьютерах

Для производства четырех видов компьютеров (С1, С2, С3 и С4) имеются[48]
комплектующие пяти видов. Необходимо спланировать выпуск компьютеров (найти значение переменных С1, С2, С3 и С4) так, чтобы:

их число было максимально;

их стоимость была максимальна.

Исходные данные по задаче сведены в таблицу:

№ компьютера		Стоимость (у. е.)		Число единиц комплектующих, идущих на один компьютер
				1		2		3		4		5
1		600		1		0		4		0		3
2		2500		1		0		8		0		8
3		25 000		0		1		0		4		15
4		60 000		0		1		0		8		64
Есть комплектующих:		100		20		500		100		1200

Подобная задача реально стоит перед людьми, собирающими компьютеры «на коленках» отверточным способом: челноки привезли детали: 1 и 2 – это, к примеру, центральные процессоры двух типов, 3 и 4 – микросхемы памяти, а 5 – платы связи с периферией; компьютеру нужно, конечно, и многое другое, но это другое (корпуса, винчестеры) имеется в избытке. Из комплектующих нужно собрать компьютеры, максимизируя вышеотмеченные целевые функции.

Трехсторонняя дуэль

А теперь автор представляет на суд читателя свою любимую задачу – задачу о трехсторонней дуэли. Вот ее условия.
Сэм, Билл и Джон договорились сразиться на дуэли втроем по следующим правилам:

жеребьевка определяет, кто стреляет первым, вторым и третьим;

дуэлянты располагаются на одинаковых расстояниях друг от друга (по углам равностороннего треугольника);

обмениваются выстрелами по очереди, определенной жребием, пока двое не будут убиты;

очередной стреляющий может стрелять в любого из живых.

Известно, что Сэм – снайпер и никогда не промахивается с данной дистанции, Билл поражает мишень в 80% случаев, а Джон – в 50%. Какова наилучшая стратегия для каждого из участников и каковы вероятности их выживания, если они следуют оптимальным стратегиям?
В этой дуэли у Сэма и Билла могут быть две тактики поведения. Нулевая – это когда стреляющий ничего не знает о меткости соперников и целит в первого подвернувшегося. Первая – когда дуэлянту известно о том, кто как стреляет, и он метит в соперника с наивысшими стрелковыми качествами в надежде остаться tête-à-tête с наихудшим стрелком.
Джон может следовать и второй тактике. Чтобы получить наивысшие шансы выйти победителем из дуэли, он должен намеренно стрелять в воздух, пока двое его соперников живы. Ведь очередной стреляющий будет бить не в него, а в более меткого противника. После того как Сэм или Билл будет убит, Джон должен показать все, на что он способен. В такой ситуации его шансы выжить составляют 50%, если он остался наедине с Сэмом, и еще больше ¾ если с Биллом.
Участник дуэли, прежде чем выстрелить, должен, во-первых, определить самого меткого соперника, в которого нужно стрелять, руководствуясь первой тактикой поведения. Для этого предназначена функция Самый_меткий (см. пункт 2 на рис. 6.36), возвращающая номер противника с наивысшими стрелковыми качествами. В ней перебором всех участников дуэли (цикл for) учитываются, естественно, только живые противники (СтатусПротивник
= “жив”) и не сам стреляющий (Противник ¹ Стрелок).

A genuinely optimum fire bucket

(Translation into English by R.Girvin)
(Russian Text)
This optimization task was easily manageable either numerically (see Etude 2) or analytically (see Etude 7). In those, we learned how to maximise the volume of a bucket given a chosen manufacturing technology: cutting a sector from a metal disk and folding the remainder into a cone. But that way the bucket lost not only optimality, but also the status of bucket: it turned into a fire bowl! It was also impossible to put on a floor, and would be useless for any purpose except as a Vietnamese hat. In our rush for Number (the volume of the bucket) we have lost Essence (the function of a bucket, its capacity for conveniently carrying liquid).
The author recalls a cartoon film based on a Norwegian fable about a goat that learned to count, and decided to count all the farm animals: "I am one; the hen is two; the pig is three, etc." But as all the animals were moving around, the process soon turned into uproar. "Oh, have you counted me?!" "Keep still, or else..!" But everything ended happily, both for the goat and the fable.
In this story, as with any other fairy tale, there's a deep wisdom. It's necessary for us to count things, but as we interact with them we can run into a conflict. Not only does Nature dislike sharp corners, but also enumeration, which in a number of cases simply kills her. This can be observed not only in biology and physics, where the tools of knowledge frequently unrecognizably spoil the object of research, but also in computer science. This applies not only when applying computers to natural sciences applications, but also when applying computers to computers.
To establish a diagnosis, a doctor has no need to know the exact numerical value for a patient's body temperature (36.6C, 38.9C, etc). It's enough to express the thermometer indications by ranges, on which 'medics' have agreed beforehand: "low", "normal", "raised", "mild fever", "high fever". The borders of these estimates, though precisely fixed, are nevertheless imprecise – 'fuzzy'. This comes not merely from modern representations in terms of fuzzy set theory (FST) but also in terms of practical reality: thermometer error, measurement technique, and so on. A graduate of a medical school can tell you, without even pausing to think, where the division between high and very high temperature lies. The skilled doctor can decide this without consciously thinking of the number, while diagnosing better than the beginner.

Even the parameters of patients that are expressed not in real numbers, but in a kind of binary – Wasserman test positive/negative, Koch bacilli present/not present, HIV positive/negative, etc. – have 'fuzzy' borders. Laboratory analysts know this well. If you glance in any therapeutic reference book, where the symptoms of illnesses are described, normally you won't see hard numbers for body temperature, arterial pressure, haemoglobin count, etc. You'll simply see a broad categorisation: "is raised", "is lowered", and so on. Perhaps this is why programs that output a diagnosis, based on patient parameters entered into a computer, have not received wide practical application. One of difficulties in this area is translation of the parameter (a number) into a symptom (a category).
There's a generally accepted identification of three recent revolutions in programming: structural, object-oriented, and visual. But this revolutionary zeal focused more on the programs (the art for its own sake) and virtually neglected the point of programming: the models of the real world, the properties, and the events programs are simulating. Moreover, in retrospective we can see certain counter-revolutions: for example, the decline of analogue computers in favour of digital engineering. Recently, though, there has been a renaissance through the revival of principles of analogue modelling on modern digital computers (for example, the MathConnex environment included with Mathcad 7 and 8 Pro: see Appendix 7). It can similarly be seen in the technology of visual programming, where the former analogue control elements – adders, integrators etc. – are reconstructed.
But the virtual nature of these neo-analogue machines means also their strict determinism, and this brings not only positive, but also negative consequences. The principles of FST have been in programmers' hands for a long time – literally. The computer mouse reacts to two events: a click, and a double click. What, actually, is the difference one double click and two single? The duration of the pause between clicks. Expressed in non-technical language – "very short", "short", "long", etc.) this is a typical example of sets with 'fuzzy' borders. How much time is needed to increase a short pause to turn it into long, so that the double click breaks up into two single? How many handfuls of grain make a heap?


At the peak of the structural programming revolution, when in all the programming 'temples' the keyword GOTO was anathema, you frequently heard such statements as: "It's practically impossible to teach good programming to students originally taught BASIC; as potential programmers they're crippled intellectually, without hope of a cure." There were also broader warnings such as "Caution! Employment in programming is a dead end career. Don't think that having learned to program, you'll achieve anything in life".
It's as if traditional programming forces the programmer to look at the Technicolor world through monochrome glasses: a binary variable can take only two values (yes/no), and a real variable, values anywhere in a stipulated range strictly determined by the length of the mantissa. The truth lies somewhere between. The extreme points of view aren't useless – they are like book-ends that stop it sliding beyond defined extremes. The intermediate truths are termed 'fuzzy'. So one might say, "If you want to learn about the world (which is fuzzy, and unquantifiable) and to deal with it, beware of the traditional programming languages and mathematical programs with their strict determinism."
But we shall return to our problem of the fire bucket, and try to solve it using FST techniques and the opinions of people (who – thank goodness! – don't need such a rigmarole to use a simple device to escape being roasted).
Let's carry out an original poll and learn as much as we can about the parameters of an optimum fire bucket: its most convenient geometry (radius of the base of the cone to the height) and its optimum volume (the weight of the filled bucket). These can then be expressed as FST rules. How much water can you add to a bucket before it turns from light to heavy? How much can you increase or reduce the radius, or the height, of a bucket before it stops being convenient? These statements are typical definers of fuzzy sets. In the Mathcad environment, as well as in other popular packages, there are no variable types for storing such objects. But nevertheless we'll try to solve the given problem (see figures 6.41, 6.42, 6.43, 6.44 and 6.45 – a solution developed with B. Usyenko). Let's break it down into steps.



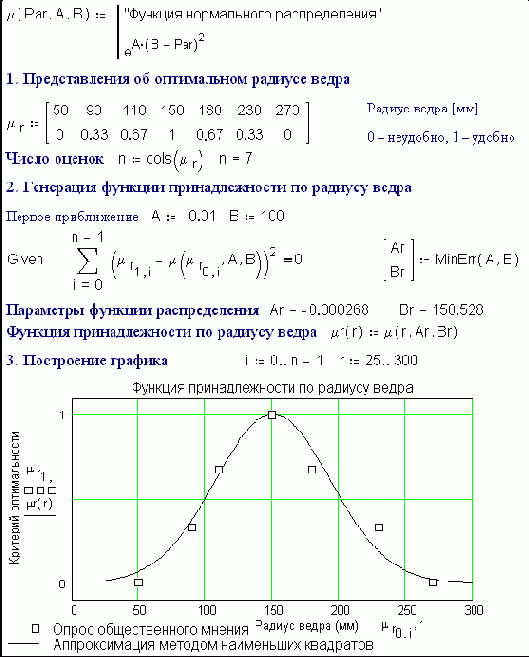
Fig. 6.41. Optimum radius of fire bucket
Step 1 (fig. 6.41). The matrix ?r stores people' s views about the optimum (most convenient) base radius r of a conical fire bucket, expressed in millimeters. This data could be gathered by making buckets of various geometries, giving them to people to try out, and then asking for estimates on a scale:

convenient (1);

more convenient than inconvenient (0.67);

more inconvenient than convenient (0.34);

inconvenient (0).

It would be possible to have more options within the range 0-1. In step 1 we have a limited familty of points, but these also could be increased; there are as many opinions as people. Readers can ask all their friends, and add new columns to the matrix [?r]
Step 2. The survey data is processed by the least squares method (see Etude 4). We can see that the data approximately fits a normal distribution curve (see figs. 6.41 and 6.42). The idea of a 'membership function' ?r for the radius of the bucket is one of the basic concepts of FST. In normal mathematics it would be considered that a certain size either belongs, or does not belong, to a particular set; in FST it's permissible to say that the size belongs to the set to some extent
(so many percent).
Step 3. The statistical processing is completed and plotted.

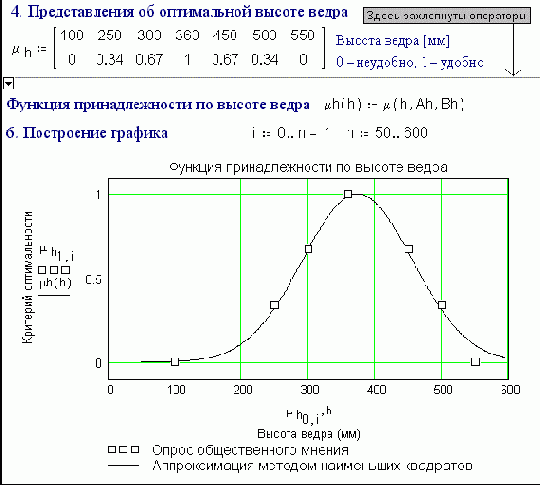
Fig. 6.42. Optimum height of a fire bucket
Steps 4-6 (fig. 6.42) repeat steps 1-3, but for a second parameter of the bucket, its height.

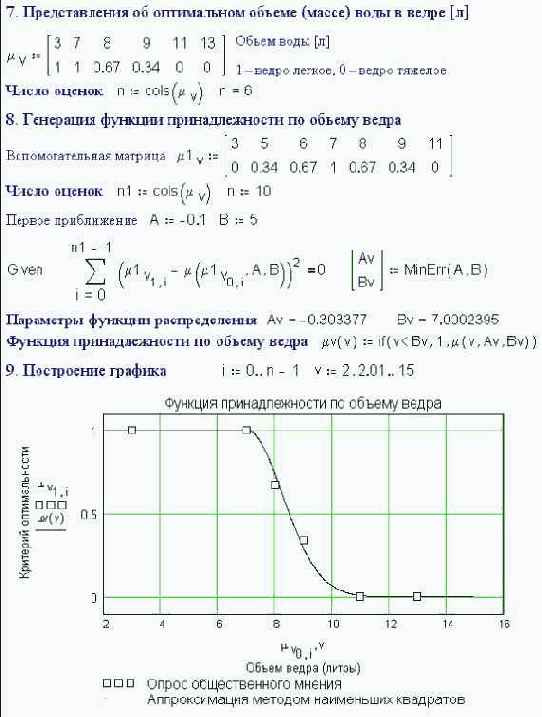
Fig. 6.43. Optimum volume of a fire bucket
Steps 7-9 repeat steps 1-3 and 1-6 for the third important parameter of the bucket, its volume (or weight – they're proportional). This is based on human estimates:

bucket is light (1);

bucket is more light than heavy (0.67);

bucket is more heavy than light (0.34):

bucket is heavy (0).

The survey data is processed as before, but using a "one-sided" cumulative distribution curve (see item 9 in a fig 6.43). (When designing technical systems, such parameters wouldn't be based on a survey but on figures provided by experts to the decision-makers).



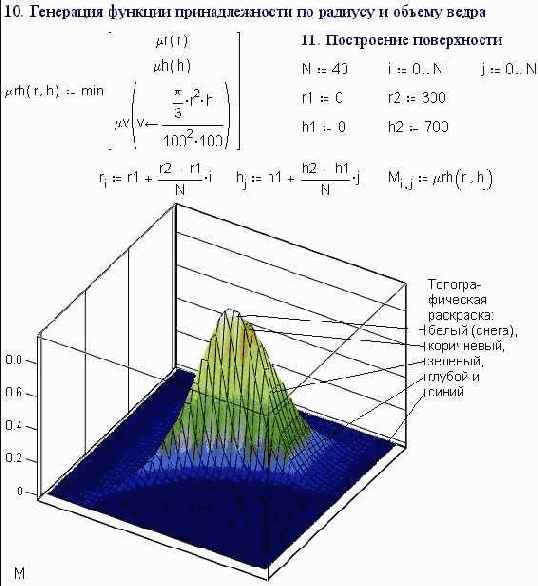
Fig. 6.44. the "Rotated" optimum fire bucket
Step 10 in fig. 6. 44 is the nucleus of the solution of our: in this, a two-parameter membership function is generated by the merging (akin to multiplication) of two single-parameter membership functions.
In FST there are no traditional concepts of addition, subtraction, multiplication etc.(those represented by the mathematical operators "+", "-", "×" etc. in the Mathcad environment). In FST, multiplication (crossing of sets – logical AND) is replaced with an operation of searching for a minimum; and addition (merging of sets – logical OR) by searching for a maximum. The mathematics of precise sets is a special case (a subset of the mathematics of fuzzy sets) where these operators/functions are genuinely equivalent. This means that in the Mathcad environment, where there are no built- in AND and OR operators, we can create equivalents using the min and max functions we described in Etude 3.
In our task the membership function mu_rh is generated by the fuzzy addition (min) of the functions mu_r, mu_h and mu_v. That is, the fuzzy set "the convenient bucket " is the intersection of three other fuzzy sets: "convenient radius of bucket" (step 1), "convenient height of bucket" (step 6) and "a not heavy bucket" (step 9).
Step 11. The top of the 'mountain' – the surface plot of function mu_rh – is the point where the parameters of most convenient fire bucket lie.

Fig. 6.45. Designing the optimum fire bucket
Step 12 (fig. 6.45). Searching for the maximum of the function mu_rh in the Mathcad environment can be done in various ways (see Etudes 2 and 3). We'll proceed this way: we'll imagine metal disks of various radius R (from 10mm-500 mm with a step of 1 mm) and cut each size into 2 to 10 identical buckets. This gives a large variety of bucket sizes and geometries, and we'll consider the optimum (the most convenient) bucket to be the one for which the membership function mu_rh is maximised.


Even the reader who hasn' t been paying much attention will notice some discrepancies and simpiflications in our analysis of this task. Three of them are:

Unlike our theoretical bucket, a real one is never filled up right to the brim ("what counts as full?" defines another fuzzy set).

The author has only loosely defined, and often confused, such concepts as "volume", "weight", and "weight of bucket".

We haven't taken into account the weight of an empty bucket, and also the material from which it is made.

However it is merely necessary to glance again at the diagrams illustrating fuzzy sets in figs. 6.41, 6.42 and 6.43
to understand a major virtue of applying FST to decision-making tasks. Our solution works in isolation, so it's possible to express the essence of a task disregarding various minor variables: the density of water, weight of the empty bucket, degree of filling, etc. This feature is now realized, for example, in automatic control systems, where regulators based on FST rules are more 'attentive' to the basic signal and less susceptible to noise. It turns out, though it seems paradoxical, that the traditional 'precise' control algorithms qualitatively lose out to 'fuzzy' ones, or are their special cases. In the field of automatic control theory, a certain stagnation could be seen until recently, as any new algorithms couldn't be compared to the older Proportional Integral Derivative (PID) control algorithm. The principles of PID control can be seen in the procedure for a bank's credit check on a client applying for a loan. The banker, in assessing the decision, considers:
1) The sum of money in the client's account (this is the proportional component: the richer the client, the larger the loan that can be offered);
2) The average sum in the account over, say, the last five years (the integrated component; checking this ensures that the client didn't borrow a million pounds the day before, to create the illusion of solvency); and


3) The rate of change of the account (the differential component, showing whether the client's business is on the rise or decline);
It's possible to take into account other factors, but three is a nice number!
The PID-control algorithm has imperceptibly become something of a fetish. Fuzzy management cames as a fresh breeze in the theory of automatic control, whose basic rules are now open to review. To be sure, there are other opinions. Some scientists believe that the use of FST in automatic control, and cybernetics in general, is just replacing one uncertainty with another ("trying to stitch soapsuds", the Russian expression goes) and that's all there is to it. Sceptics explain away the observed improvement in control quality to our devoting more attention to regulator technology (as if the ritual of attention could improve performance). Besides some researchers believe that FST, since it dates back 30 years (it was devised by the Iranian-American Dr Lotfi Zadeh at UC/Berkeley in the 1960s) is old and best forgotten.
Actually, the skip from a task about a tripartite duel to one about an optimum bucket wasn't entirely casual. Traditionally, precise sets are illustrated by circles with sharply delineated borders. Fuzzy sets are drawn as circles formed of separate dots, with a high density at the centre and thinning to zero (as if evaporating) towards the edges. Such 'fuzzy set' images can be seen on a firing range wall where targets are hung. The bullet traces form a probability distribution, whose mathematics is well-known. It appears that the theory for working on fuzzy sets, as probabilistic distributions, has already existed for a long time...
We keep talking about fuzzy sets. But are they – mathematically – actually sets? To be consistent, it's necessary to ascertain that the fuzzy set has elements (fuzzy subsets, fuzzy sub-subsets, etc). We'll return to a classical example: a heap of grain. An element of this fuzzy set will be, say, a million grains. But a million grains is not a precise element: it's a fuzzy subset. If you count out grains, whether manually or automatically), it's no wonder that you might mistake, say, 999 997 grains for a million. In FST terminology, you could say that the element 999 997 has a 'membership value' 0.999997 for the fuzzy set {a million grains}. Besides, even "a grain" is not a precise element, and is another fuzzy subset: it might be a high-grade grain, but there are also underdeveloped grains, grain fragments, and bits of husk. Depending which way you decide, you might count one grain as two, or vice versa.


The fuzzy set isn' t very easily accommodated in the digital computer with classical data constructs: elements of a file (a vector) should be new files of files (composed of vectors and matrices, in the case of Mathcad). The classical mathematics of precise sets (number theory, arithmetic, etc) is rather like a hook, with the help of which we anchor ourselves on the slippery and fuzzy environmental world. And a hook is a rough implement, quite often damaging what it's embedded in. The terms describing fuzzy set membership values (there are plenty in this book and others – "much", "some", "a few", and so on) are difficult to make into programming statements because they're contextually dependent. It's one business to say, "Give me a few sunflower seeds" to someone with a cupful, and another to say the same to a driver hauling a lorryload.
Whether it is possible to see a certain crisis in theory and practice of programming connected with contradict between precise structure of the programs (data) and fuzzy world? Is it necessary to develop fuzzy programming languages for implementation fuzzy algorithms that accommodate fuzzy data? Opinions vary. In the author's view, programmers (and they have the last word) have learned poorly how to cram the fuzzy world into the strictly determined computer. Figs. 6.41, 6.42, 6.43, 6.44
and 6.45 are an example.

По-настоящему оптимальное пожарное ведро (English version of text)

Эта оптимизационная задача хорошо решается и численно (см. этюд 2), и аналитически (см. этюд 7). В ней под оптимизацией мы понимали максимизацию
объема ведра при выбранной технологии его изготовления (вырезание сектора из круглой заготовки). Но при этом ведро теряло не только свою оптимальность, но и свое звание ведра: оно превращалось в пожарный тазик (его тоже нельзя поставить на пол и использовать не по назначению) или во вьетнамскую шляпу. Мы гнались за Числом (объем ведра) и потеряли Суть (функцию ведра – емкость для удобной переноски жидкости).
Тут автору вспоминается мультфильм о козленке, который научился считать и всех встречных-поперечных пересчитывал: «Я – это раз, петух – это два, свинья – это три и т.д.» У козленка из-за этого со всей пересчитанной живностью возникали крупные неприятности: «Ах! Ты меня сосчитал?! Ну, держись!» Но все кончилось хорошо. На то она и сказка.
В этой истории, как и в любой другой запоминающейся сказке, есть глубокий смысл. Стоит нам что-то пересчитать, как мы вступаем с этой пересчитанной субстанцией в глубокий конфликт. Природа не любит не только острых углов, но и счёта, который в ряде случаев просто убивает ее. Это можно наблюдать не только в биологии и физике, где инструменты познания часто неузнаваемо портят сам объект исследования, но и в computer science. И не только в области приложения компьютеров (счёта, грубо говоря) к решению естественнонаучных задач[54], но и в области применения компьютеров к самим компьютерам.
Врачу для установления диагноза незачем знать числовое значение температуры тела больного – 36.6, 38.9 и т.д. Достаточно выразить показания термометра диапазонами (категориями), о которых медики договорились заранее – «температура пониженная», «нормальная», «повышенная», «высокая», «очень высокая» («жар»)[55]. Границы этих оценок хоть и четко зафиксированы, но тем не менее размыты – «пушисты». Это определяется не только современными представлениями ТНМ, но и погрешностью самого термометра, методикой измерения температуры и др. Выпускник медицинского вуза не задумываясь скажет вам, где лежит граница между высокой и очень высокой температурой. Опытный же врач может этого и не знать, хотя диагнозы он выставляет не хуже начинающего доктора. Даже параметры больного, выраженные не в вещественном, а в булевом виде (реакция Вассермана, наличие палочки Коха, анализ на СПИД и т.д.), имеют «пушистые» границы. Об этом хорошо знают лаборанты, проводящие анализы. Если заглянуть в любой справочник терапевта, где описаны симптомы болезней, то, как правило, конкретных чисел (температура тела, артериальное давление, содержание гемоглобина в крови и т.д.) там не увидишь. Одни слова – повышено, понижено и т.д. Программы выставления диагноза по введенным в компьютер параметрам больного не получили широкого практического применения. Одна из трудностей в этом деле – перевод параметра (числа) в симптом (категорию).

Принято выделять три революции, переводившие программирование на новые уровни: структурное, обьектно-ориентированное и визуальное. Но эта революционность была больше обращена на программы
(искусство ради искусства) и почти не касалась объекта программирования – тех моделей реального мира, свойства и события которого программно имитируются. Более того, ретроспективный взгляд может уловить и некую контрреволюционность в отказе, например, от аналоговых вычислительных машин и переход к цифровой технике. Хотя в последнее время здесь наблюдается какое-то подобие ренессанса – возрождение принципов аналогового моделирования на современных цифровых компьютерах (пример – среда MathConnex в составе Mathcad 7 и 8 Pro: см. приложение 7). Это можно отметить и в технологии визуального программирования, где воссоздаются прежние элементы управления (controls) – аналоги сумматоров, интеграторов и др. Но виртуальность этих неоаналоговых машин подразумевает и их строгую детерминированность (четкость), что влечет за собой не только положительные, но и отрицательные последствия. Сами же принципы ТНМ давно уже у программистов под рукой. В буквальном смысле. Мышка компьютера реагирует на два события – щелчок (click) и двойной щелчок (double click). А чем, собственно, один двойной щелчок отличается от двух одинарных? В длительности паузы между щелчками. Если ее выразить на языке человеческого общения (очень короткая, короткая, длинная и т.д.), то это будет типичным примером множеств с «пушистыми» границами. На сколько нужно увеличить короткую паузу, чтобы она превратилась в длинную и чтобы двойной щелчок распался на два одинарных? А сколько зернышек нужно добавить в горсть, чтобы она превратилась в кучу[56]?
В разгар структурной революции, когда во всех программистских «храмах» предавали анафеме ключевое слово GOTO[57], часто можно было услышать такую фразу: «Практически невозможно научить хорошо программировать студентов, ориентированных первоначально на BASIC: как потенциальные программисты они умственно оболванены без надежды на исцеление». Встречались и более категоричные предупреждения типа: «Осторожно! Занятие программированием может лишить вас будущего. Не думайте, что научившись программировать, вы чего-то добьетесь в жизни». Традиционное программирование как бы заставляет программиста смотреть на многоцветный мир сквозь черно-белые очки: булева переменная может принимать только два значения (да-нет), а вещественная – строго определенное в оговоренном диапазоне с фиксированной длиной мантиссы и т.д. Истина лежит посередине. Но и крайние точки зрения не бесполезны – они как бы подпирают истину с двух сторон, не давая ей скатиться к крайностям. Да и сами истины в чем-то «пушисты». А одна из них может звучать так: «Если хочешь познать мир (нечеткий, «пушистый», бесчисловой) и управлять им, то опасайся традиционных языков программирования и математических программ с их строгой детерминированностью».


Но вернемся к нашей задаче о пожарном ведре и попытаемся решить ее уже с привлечением аппарата ТНМ и с учетом мнения людей, которым – не дай Бог! – придется воспользоваться этим нехитрым средством пожаротушения.
Проведем своеобразный опрос общественного мнения и узнаем как можно больше о параметрах оптимального пожарного ведра: о его удобной[58] геометрии (радиусе основания конуса и высоте) и о его оптимальном объеме (о весе ведра с водой). Вот здесь-то и проявятся во всей своей красе положения ТНМ. Сколько нужно добавить в ведро воды, чтобы оно из легкого превратилось в тяжелое? На сколько нужно увеличить или уменьшить радиус или высоту ведра, чтобы оно перестало быть удобным? Вот эти сколько и являются типичными представителями нечетных множеств. В среде Mathcad, как и в других популярных пакетах, нет типов переменных для хранения таких величин. Но мы тем не менее мы постараемся решить поставленную задачу (рис. 6.41-6.45 – задача решена совместно с В.Усенко). Разберем ее по пунктам.

Tutti-frutti

Ниже приводится ряд программ, написанных на языке Mathcad и решающих самые разнообразные задачи (tutti-frutti по-итальянски – всякая всячина): оптимизация, головоломка, статистика, теория вероятностей...

Команды символьных преобразований

На рис. 7.1
даны примеры выполнения некоторых команд символьной математики из меню Symbolic.

Операторы символьных преобразований

Эти операторы позволяют работать со средствами символьной математики уже не в ручном (см. рис. 7.1-7.5), а в автоматическом
режиме. В среде Mathcad знак «=» означает числовой, а знак «®» – символьный вывод значения переменной, функции или выражения, записанного от этого знака. В ряде случаев оператор «®» более удобен, чем оператор «=». Автор не смог удержаться и уже в этюде 1 на рис. 1.4 и на рис. 1.14 вел расчеты через оператор «®».
На рис. 7.6 даны типовые примеры работы оператора «®»: взятие производных разных порядков (пункт 1), вычисление неопределенного интеграла[19]
и определенного интеграла с бесконечным верхним пределом (пункт 2), вычисление суммы (пункт 3) и произведения (пункт 4), взятия пределов.

Оптимизация численных расчетов

Третий инструмент символьной математики пакета Mathcad, который позволяет с определенной долей условности назвать его системой искусственного интеллекта[35], связан с оптимизацией численных расчетов. Вспомним исторический анекдот, приписываемый королю математиков – Гауссу (см. сноску 17).
...До конца урока оставалось десять минут, и учитель решил отдохнуть – он занял учеников, среди которых был и маленький Гаусс, рутинной работой – подсчетом суммы чисел натурального ряда от 1 до 100. Но через мгновение Гаусс поднял руку и выдал ответ – 5050. Он не стал складывать единицу с двойкой, полученную тройку с тройкой и т.д., а... перемножил сумму первого и последнего членов ряда на 50. Ведь сумма второго и предпоследнего членов также равна 101, как и сумма третьего и предпредпоследнего, а таких пар в сотне ровно пятьдесят.
Посмотрим, как среда Mathcad следует примеру не только маленького, но и взрослого Гаусса.

Идеология

В начале было Слово...
Начало Евангелия от Иоанна утверждает примат Слова. А вот как начинается «евангелие» от фирмы Waterloo Maple, Inc., описание пакета Maple: «Maple V is a Symbolic Computation System or Computer Algebra System». Этим декларируется, что в Maple главенствует Символ (выражение, уравнение, функция и т.д.), а не Число. Разработчики сразу оговаривают, что Maple – это математика, а не вычислительная математика. За прилагательными в названиях научных дисциплин нередко таится некая ущербность[46], которая хорошо иллюстрируется гипотетическим диалогом на Шаболовке: «Папа, кто построил эту башню?» – «Инженер Шухов». – «Это как наша мама – инженер?» – «Нет, сынок, наша мама – старший инженер». Пакет Maple с самого начала был задумал и реализован сугубо как инструмент символьных преобразований. В среде Maple пользователи оперируют исключительно символами, «опускаются» до числа крайне редко и, можно сказать, крайне неохотно – когда, например, не удается аналитически решить дифференциальное уравнение и приходится использовать численные методы.
Пакет же Mathcad изначально создавался для численного решения математических задач (1988 г.). Инструменты символьной математики были интегрированы в Mathcad совсем недавно (1994 г. – четвертая версия). За свою десятилетнюю историю пакет Mathcad как бы повторил многовековой путь развития самой математики, в которой долгое время господствовало число (арифметика, геометрия) и только на пороге новой истории появился символ (алгебра, математический анализ). Но многие пользователи Mathcad по-прежнему считают символьную математику рекламной штучкой, выполняющей лишь вспомогательные и демонстрационные функции.
Считается, что Maple – это университетская компьютерная математика, а Mathcad – математика технических вузов. И не только потому, что первый пакет опирается на символ, а второй – на число. Решение математических задач в среде Maple требует как умения оперировать той или иной встроенной функцией, так и основательного знания методов решения, в нее заложенных: во многих встроенных функциях Maple фигурирует аргумент, задающий метод решения. Что такое корень уравнения и какая функция (процедура) может его отыскать – знает каждый, кто использует математические пакеты, но какие методы при этом применяются – для многих тайна за семью печатями. Одну из таких «тайн» мы пытались раскрыть на рис. 3.1, анализируя функцию root.

Интерфейс

В столицах женщины получают, может быть, лучшее образование; но навык света скоро сглаживает характер и делает души столь же однообразными, как и головные уборы.
А.С.Пушкин. Барышня-крестьянка
Пушкин говорит о том, что без индивидуальности не может быть ни настоящей красоты, ни настоящего величия. Индивидуальность того или иного пакета проявляется не только в наборе математических инструментов (душа), но и в интерфейсе (внешность). Если говорить о наиболее распространенных версиях Mathcad и Maple (существуют их версии для разных платформ – DOS, Windows, Mac[47], UNIX...), то, перефразируя Пушкина, можно сказать, что в среде Windows прикладные программы получают, может быть, лучшие возможности для связи с другими приложениями и периферией; но идеология Windows скоро сглаживает программы и делает их столь же однообразными, как их интерфейс.
«Душа» Maple ведет свою родословную от fortran[48], вернее от богатых математических библиотек, наработанных за долгую жизнь этого языка. Первые элементы компьютерной алгебры появились именно в нем: ввел, например, программист строку a = (x**2 - y **2) / (x - y), а компилироваться будет уже другая, упрощенная – a = x + y. В свою очередь, интерфейс Maple – это не что иное, как режим немедленного выполнения операторов языка BASIC.
Все слышали о трех революциях в программировании: структурной (ее отголоски звучали в этюде 6, когда мы рассуждали о метке в программе), объектно-ориентированной и визуальной. Но мало кто помнит, что настоящую, и в каком-то смысле единственную революцию в программировании совершил BASIC-интерпретатор. В «дореволюционное» время нужно было сначала писать программу, затем компилировать ее в машинные коды и только потом – получить результат. Пользователь не видел промежуточных результатов и не мог вовремя вмешаться в вычислительный процесс. Из-за этого основная масса распечаток шла прямиком в мусорную корзину. С языком BASIC пришла новая технология. Открыв любой старый учебник по этому языку, можно прочитать: «Если в начале вводимой строки стоит номер, то эта строка становится строкой создаваемой (редактируемой) программы. Если номера у строки нет, то операторы строки немедленно
выполняются после нажатия клавиши Enter». На рис. 7.19 приведен протокол немедленного выполнения операторов в среде языка GW-BASIC, входящего в состав MS-DOS 3.x. Пример простой, но за ним стоит многое.
Ok
a = 3: print a: REM Исходная величина
 3
Ok
b = a^(1/77): print b
 1.01437
Ok
c = TAN(b)^99: print c
 2.605988E+20
Ok
d = ATN(c^(1/99)): print d
 1.01437
Ok
e = d^77: print using"#.##############";e
3.00000071525574
Ok

Структура данных

Не спеши выполнять приказ: очень вероятно, что его отменят.
Армейский и деловой фольклор
Вышеприведенная трилингва BASIC-Mathcad-Maple не только поясняет особенности интерфейса при работе в этих средах, но затрагивает и более глубокие пласты. Ахиллесова пята численных методов – это погрешность расчетов. Очень часто даже самая мизерная ошибка вычислений искажает расчет и может свести на нет ценность результата. Символьная компьютерная математика протаскивает через чащу преобразований исходную величину в ее первозданном виде: на рис. 7.21 во всех многоэтажных формулах, как в скорлупе, сидит исходная тройка. «Не спеши выполнять приказ: очень вероятно, что его отменят» – это бюрократическое правило порождает не только волокиту, но и амортизирует неразумные распоряжения начальства и просьбы посетителей. Maple не спешит переводить число в традиционную форму (в вещественное число с плавающей запятой, например) и не попадает в ловушку, подобную той, какая проиллюстрирована на рис. 7.19 и 7.20 (исчезновение тройки). Функция evalf в среде Maple может возвратить значение переменной длиной до 500000 знаков. Но тройку из выражения, хранимого в переменной е, абсолютно безошибочно и сверхбыстро может извлечь («разбить скорлупу») первая и в каком-то в смысле главная функция символьной математики – simplify (упростить). Одним словом: не спеши вычислять – очень вероятно, что это не понадобится[50].
Протоколы на рис. 7.19 и 7.20 – это, в сущности, реализация на компьютере детской игры в испорченный телефон. Игрок а задумывает слово и шепчет его с небольшими искажениями игроку b, тот – игроку c и т.д. Слово по цепочке переходит к последнему игроку, который громко называет то, что услышал от соседа. Игрок a называет исходное слово, и тут раздается хохот – спутник любой игры. Но искажения чисел компьютером вызывают не смех, а слезы. Переход от числа к символу при решении задач на компьютере по значимости можно сравнить с переходом от аналогового к цифровому
способу записи звука и изображения.

Символьная форма хранения числа позволяет решить не только проблему точности, но и проблему экономии памяти компьютера: например, корень из трех, записанный в символьном виде (Ö3), хранит 1,73... (до бесконечности). Программисту при работе с Maple уже не надо ломать голову над выбором типа переменных (одинарная, двойная и прочая точность). Если говорить о сверхточности, обеспечиваемой «длинными» типами переменных, не следует забывать, что природа не любит не только острых углов, но и избыточности. Если решение «разваливается», это может свидетельствовать не только о дефекте в вычислительной процедуре, но и о неправильной исходной модели. Вот еще один диалог, но уже не на Шаболовке, а в музее. Экскурсовод: «Этому экспонату один миллиард и двадцать лет». – Посетитель: «Откуда такая точность?!» – Экскурсовод: «Когда я поступил сюда на работу, мне сказали, что этому экспонату миллиард лет, а с тех пор прошло еще двадцать». Подобной излишней педантичностью страдает и автор: на многих рисунках книги в расчетах оператором «=» выводятся все 15 знаков числа, хотя там достаточно трех-четырех.
Переменные в среде Maple могут хранить (естественно, в символьном виде) все что угодно: константу, выражение, функцию, равенство, неравенство, график, геометрический образ и т.д. Сами же переменные группируются в последовательности (sequence), массивы (array), списки (list), множества (set) и таблицы (table). Элементом массива может быть список, элементом списка – массив и т.д. Комбинируя структуры и создавая новые, пользователь способен моделировать довольно сложные математические абстракции, ограничивая себя лишь своей фантазией и объемом памяти компьютера. По знаменитой формуле Вирта: программа – это алгоритм плюс структура данных. Говоря о Maple, можно сказать, что протокол решения задачи – это умело спроектированная структура символьных данных, процеженных сквозь сито функций и команд. В Maple встроен fortran-подобный язык, позволяющий реализовывать сложные алгоритмы, но к программированию прибегают в особых случаях – Maple и Mathcad задумывались как средства программирования без программирования (в те времена слова «работа на компьютере» и «программирование» были почти синонимами). К программированию и в среде Maple, и в среде Mathcad прибегают в тех случаях, когда для решения задач не хватает встроенных средств (см. этюд 6).
Существует ошибочный взгляд на компьютерную символьную математику как на вычислительную математику без погрешностей и ошибок. Пример, приведенный на рис. 7.22, опровергает это мнение[51].

Примеры

Лучше один раз увидеть, чем сто раз услышать.
Русская пословица
Нет ничего практичней хорошей теории и нет ничего численней хорошего аналитического решения задачи. Пример, приведенный на рис. 7.23, особо поражает тех, кто занимается или когда-то занимался составлением программ решения дифференциальных уравнений. В среде Maple эта задача решается буквально в два счета: делай раз – запись уравнения (рис. 7.23), делай два – его решение в аналитическом виде.

Графика

По одежке встречают, по уму провожают.
Русская пословица
«Одежка» всех математических пакетов – это их графика. Красочные объемные конструкции, подобные той, которая завершает решение задачи о балке (см. рис. 7.25), помещают в рекламных буклетах, на обложках описаний и на коробках с дистрибутивами всех математических программ. В среде Mathcad фактически нет графиков функции, а есть только визуализация данных, хранящихся в векторах и матрицах. В среде Maple достаточно иметь только вид функции одной или двух переменных, чтобы строить самые сложные графики (декартов, полярный, с логарифмическими шкалами осей, параметрический) и поверхности (в декартовых, сферических, цилиндрических (см. рис. 7.25), спиральных координатах). Также в среде Maple допустима визуализация данных из векторов и матриц.
Вот еще ряд существенных преимуществ графики Maple по сравнению с графикой Mathcad:
• в среде Mathcad поверхность может строиться только в прямоугольной области существования двух аргументов, а в среде Maple это ограничение снято: границы области существования графика можно задавать и аналитически (пример – рис. 7.27);
• в среде Maple допустимо в одной области документа через функцию display помещать разнотипные графики: комбинировать, например, декартов и полярный график, цилиндр со сферой и т.д., если в этом есть, конечно, какой-то математический смысл. Математический смысл конструкции в пункте 5 на рис. 7.25 отыскать довольно сложно. Тут у нас получилась задача не о балке, а о проектировании вазы необычной формы, которую уместно поставить в офисе фирмы, разрабатывающей или продающей математические пакеты;
• в среде Maple создание и форматирование графиков возможно не только через меню (как в среде Mathcad), но и через параметры (ключи) соответствующих команд. Это позволяет программно управлять графикой: если какая-то кривая выходит за отведенные ей пределы, то она автоматически «краснеет», и т.д.;
• в среде Maple есть специальный тип графики, ориентированный на визуализацию решений задач определенного класса: дифференциальных уравнений, определения области существования аргументов, конформных преобразований, поиска множества корней, линейного программирования (рис. 7.29) и т.д.;
• Maple допускает построение различных геометрических абстракций (линий, фигур, тел) через задание их параметров.

Программирование

А роза упала на лапу Азора
А.Фет
Средства реализации сложных алгоритмов были введены только в версию Mathcad PLUS 6.0 (1995 г. – см. этюд 6). Maple же с самого начала задумывался как язык управления символьными преобразованиями. Его команды, как уже было отмечено ранее, выполняются немедленно после нажатия клавиши Enter. Но ничто не мешает собрать эти команды воедино и сформировать из них новые функции и процедуры, поместить их в тело цикла или альтернативы и т.д.
В описании Maple сказано, что это fortran-подобный язык. Под этим подразумевается, что он не prolog-подобный, не APL-подобный и не lisp-подобный (на языке lisp в 1958 году John McCarthy написал программу поиска производных функций, которая стала «первой ласточкой» компьютерной символьной математики), но скорее BASIC-подобный. И не только из-за возможности непосредственного выполнения операторов, но и из-за своего синтаксиса. Различия – в деталях. Разработчики языка Maple, по-видимому, увлекаются палиндромами – текстами, которые читаются одинаково слева направо и справа налево (см. эпиграф). В языке Maple альтернатива, как и во всех других языках, начинается с ключевого слова IF, а заканчивается новым ключевым словом FI (IF наоборот). Такая же заготовка-палиндром (DO...OD) предусмотрена для тела цикла и т.д. Программисту наконец-то открывается широкая возможность написания программ-палиндромов типа IF A THEN NEHT A FI. Написание стихов-палиндромов относится к области экспериментальной поэзии (В.Хлебников и др.). Язык Maple может быть инструментом экспериментального программирования. Автор одно время был очень увлечен экспериментальным программированием. В его коллекции есть, например, программа численного интегрирования методом прямоугольников, состоящая из прямоугольных блоков. Другая программа рассчитывает числа Фибоначчи: число знаков в каждой ее строке совпадает с числами Фибоначчи. Третья программа ищет минимум функции методом золотого сечения. Она вписана в рамки структурной диаграммы, стороны которой находятся в золотом соотношении.

Язык Maple обладает всеми качествами «настоящего» языка программирования. Так, язык Maple оснащен средствами отладки, чего, к сожалению, нет у языка Mathcad.
Maple состоит из ядра (kernel), написанного на языке С и включающего в себя поддержку основных функций. Из ядра пакета можно вызывать большое количество библиотек (см. на рисунках команду with(название библиотеки), написанных на языке Maple. В Release 4 насчитывается 31 библиотека: combinat, combstruct, DEtools, difforms, Domains, finance, GaussInt, genfunc, geometry, grobner, group, inttrans, liesymm, linalg, logic, LREtools, networks, numapprox, numtheory, orthopoly, padic, plots, plottools, powseries, process, simplex, stats, student, sumtools, tensor и totorder. Такой набор инструментов определяет и высокую цену пакета[53]. Кроме того, он требует защиты – Maple V Release 4 работает только с электронным ключом. Все библиотеки съедают до 24 Мбайт дискового пространства.
Но здесь кроется и одна из главных причин того, что у нас пакет Maple менее популярен, чем Mathcad. Приобретая Maple, пользователь получает своеобразный «подарочный набор», включающий в себя вещи, которые ему никогда не понадобятся. Кроме того, универсальность очень часто (увы!) подразумевает облегченность – нельзя объять необъятное. Автор, к примеру, протестировал библиотеку simplex (решение задач линейного программирования симплекс-методом). С учебными задачами она справляется, но если их слегка усложнить, то ответа можно и не дождаться. Maple явно перегружен. Из-за этого, например, многие одноименные встроенные функции имеют разное содержание и разные аргументы после загрузки разных пакетов.
Разработчики Mathcad «пошли иным путем». Они сделали ставку на электронные учебники
и Internet. Нужно пользователю решить дифференциальное уравнение – он либо покупает отдельно соответствующий электронный учебник, который содержит описание задачи и функции, обеспечивающие ее решение, либо через Internet открывает на отдаленном сервере файл с прототипом задачи. Если пользователю Mathcad требуется неординарная графика, то он может воспользоваться пакетом Axum. Одновременно с Maple V Release 4 (лето 1996 года) на рынке появилась новая версия Mathcad под названием StudyWorks. Она стоит около 50 долл., содержит мультимедийный обучающий курс и, главное, как и Mathcad 8 Pro, предоставляет пользователям широкие возможности коллективной работы через Internet. Платой за использование чужих открытых библиотек должна быть разработка и открытие миру своих собственных.

Вывод

Право, какое затруднение – выбор! Если бы один, ну два пакета, а то – четыре. Как хочешь, так и выбирай! И Mathcad недурен (правда, худощав – всего 250 встроенных функций), и Maple неплох, и Mathematica, хоть и толстовата (несколько тысяч встроенных функций, операторов и команд), – тоже видный пакет, да и MatLab не без достоинств. Как тут быть?
Автор пошел по простому пути – он взял монолог Агафьи Тихоновны из гоголевской «Женитьбы» и заменил в нем названия женихов на названия популярных математических пакетов. Агафья Тихоновна, если помните, мечтала о том, чтобы «губы Никанора Ивановича да приставить к носу Ивана Кузьмича, да взять сколько-нибудь развязности, какая у Балтазара Балтазаровича, да, пожалуй, прибавить к этому еще дородности Ивана Павловича...». Пользователь математических пакетов, к счастью, может их интегрировать, решая поставленную задачу. Настоящий раздел книги – это своеобразные смотрины двух современных математических программ – Mathcad и Maple.
Mathcad в каком-то смысле универсальный, но не специализированный пакет. В нем есть и средства решения уравнений и систем (алгебраических и дифференциальных), и средства оптимизации, и научная графика, и символьная математика, и линейная алгебра, и статистика, и многое другое. Однако если пользователю, к примеру, нужно углубиться в символьную математику, то ему лучше работать не с Mathcad, а с Maple. Серьезные задачи линейной алгебры требуют MatLab и т.д. Многие ругают Mathcad, сравнивая его с MatLab или с пакетом Mathematica, забывая при этом, что MatLab и Mathematica стоят почти на порядок дороже Mathcad.
Ниже приводится еще несколько задач, решенных и в среде Mathcad и в среде Maple.
На рис 7.26 показано, как в среде Maple решается задача из этюда 2 о пожарном ведре (см. рис. 2.2).

От Mathcad к Maple

Один из разделов лингвистики, называемый сравнительным языкознанием, позволяет выводить общие закономерности, присущие различным языкам. На сравнительном языкознании, как правило, основывается изучение иностранных языков: одно дело учить английскому немца, а другое – китайца. Примерно такой же подход наблюдается и в освоении программных сред: одно дело приступить к работе с Maple, имея опыт общения только с традиционными языками программирования, а другое – набив руку на Mathcad. В этом – ключ к пониманию следующего раздела книги. Рассказывая о математической программе Maple V[45], автор сравнивает ее с программой Mathcad и с языком BASIC.
Мы уже упоминали о том, что символьная математика Mathcad взята из пакета Maple. Из-за этого символьное решение задачи в среде Mathcad нередко приводит к результату, понятному только пользователю Maple, идеологию и структуру которого автор попытался описать ниже.

Гибридное решение задачи на компьютере

Два числа можно сложить, переведя их в двоичную систему (разложив на нули и единицы), пропустив через лабиринт логических операций процессора компьютера и сделав обратное преобразование полученной суммы из двоичного в десятичное представление. Так работают электронные цифровые вычислительные машины
– ЭЦВМ. С числами можно поступить иначе: взять, например, два переменных сопротивления, соединить их параллельно и подать на них напряжение. Изменяя величину сопротивлений (выставляя два слагаемых
- ток, проходящий через сопротивления) и замеряя общий ток, можно найти искомую сумму. Так работают аналоговые вычислительные машины (АВМ) – аналог сложения берется из области физики электричества (закон Ома, закон Кирхгофа и др.). Если нужно решить систему дифференциальных уравнений (а это был «хлеб» аналоговых машин), то в дело шли законы электромагнитной индукции (Максвелл & Co): конденсатор – дифференцирование, катушка – интегрирование и т.д. Кроме электрических были (а где-то еще и есть) механические, гидравлические и даже пневматические аналоговые вычислительные машины.
А вы ноктюрн сыграть смогли бы на флейте водосточных труб?
А вы в DOOM сыграть смогли бы на пневмо-АМВ?
Красивую в своей простоте управляющую механическую АВМ можно видеть в музеях истории техники (в московском Политехническом, например). Она стоит на старых паровых машинах: два металлических шара вращаются на системе рычагов и регулируют подачу пара в цилиндры так, чтобы скорость хода была постоянной при любой нагрузке. Менее изящную, но тем не менее также очень полезную гидравлическую управляющую АВМ можно увидеть не выходя из дома – заглянув в бачок, пардон, унитаза.
Были времена[54], когда АВМ и ЭЦВМ работали на равных, и пользователи (вернее программисты и операторы, пользователей тогда еще и в помине не было) остро ощущали их плюсы и минусы. Стремление к приумножению достоинств и к ликвидации недостатков вызвало к жизни так называемые гибридные
машины, решающие вычислительные задачи и аналоговыми и цифровыми средствами. Сигнал, подаваемый на осциллограф (решение дифференциального уравнения на аналоговой части машины), обрабатывался в ее цифровой части: выдавалась таблица решения, велась аппроксимация и т.д. Но бурное развитие ЭЦВМ (в первую очередь резкое снижение их цены) похоронило как аналоговые, так и гибридные машины. Сейчас эта ветвь развития кибернетики практически обрублена. А жаль. Величайшую тайну природы – секрет работы головного мозга – нужно исследовать не по линии цифровых, а по линии аналоговых машин (био-АВМ!). Страшно даже представить, что у нас в голове шевелятся не извилины, а какие-то там нули и единицы.

Гибридность решения задачи в среде Mathcad в полной мере проявляется при включенном режиме Optimize (Оптимизировать – см. раздел 7.3). В этом режиме пакет, столкнувшись с численной задачей (вычисление определенного интеграла, например), не будет сразу вызывать соответствующую процедуру, реализующую метод Ромберга, а постарается найти первообразную подынтегрального выражения и работать уже с ней. Но вот тривиальный пример – определенный интеграл от a до a. Человек и без численных методов и без символьной математики знает, что он равен нулю. А что будет делать машина? Среда Mathcad с выключенным режимом оптимизации также сразу выдаст нуль. А с оптимизацией она будет долго и упорно искать первообразную для подынтегрального выражения... У автора в запасе есть набор примеров подшучивания над Mathcad (см. начало этюда 3), ставящих на место любую сверхумную систему и показывающих, что человек еще долго будет царем природы – как живой, так и неживой.
Механизм аналитических преобразований, введенный в Mathcad, придал его старым «цифровым» встроенным функциям свойство, которое с определенной долей условности можно назвать полиморфизмом[56]. Пример – функция Find. Если за ней поставить знак «=», то будет выведено числовое
значение решения системы алгебраических уравнений, а если знак «®», то – аналитическое.
Функция Find (как и многие другие встроенные функции Mathcad) несколько странная, и мы это уже отмечали. Все нормальные функции возвращают свое значение в зависимости от своего имени, числа и значений аргументов (принцип инкапсуляции, если опять же оперировать терминами объектно-ориентированного программирования; механизм вложения функций, широко используемый в Mathcad, заставляет вспомнить и о третьем «ките» ООП – о механизме наследования). Так вот, функция Find возвращает свое значение в зависимости от того, что находится около нее до ключевого слова Given.
Работая с Mathcad, под гибридностью следует понимать сочетание аналитических, численных и интуитивных методов решения задачи, что проиллюстрировано примером на рис. 7.31. Решается все та же нами любимая задача об одном пожарном ведре (пункт 1) и о двух пожарных ведрах (пункт 2). При решении задачи формируются две функции пользователя r(a) и h(a) – радиус и высота конуса, размеры которых зависят от параметров раскроя круглой заготовки (см. схему на рис. 2.1). Из этих функций строится выражение для расчета объема ведра, от которого берется производная[57].

Example 8. As the author sold the programs

(Russian text)
(Another articles of V.Ochkov)
Michael Zhvanetsky is often asked where he took themes for his miniature. «I look through the window and listen to the conversations in the street» – it is the reply of great satirist». «And how do you keep in mind all these?» – new question is followed. «Oh, I can not forget them!».
Worldly plots are worth to collect for writing computer etudes. It is the hobby of this book’s author.
The author’s profession is the teacher of the institute (Moscow Power Engineering Institute), where he gives  courses by informatics and adjacent disciplines. He directs the group of technologist and programmers too. They work out the teaching programs and computer trainer for thermoelectric power station and nuclear power station[1]. Our programs are necessary for Power Stations and power mergers. But the notorious crisis of non-payments prevents to buy them. Such computer etude took place in March 1997.
The join-stock company Tambov-power had not got free money but wanted to buy our programs. The electric power is necessary for Kotovsky paint and varnish plant (PVP-Tambovskay region.) for production. Paint requires Moscow Power Engineering Institute for repair the lecture-halls. Our scientific group is necessary new computer «iron», tools and of course wages. For solving such programs people invented money[2]
at dawn of civilization. The natural exchange-barter[3]
revived transfer of our country from something unreal to market. As we have written previously there is not only one link for the chain was locked. Fortunately MPEI got some computers. Two of them we exchanged to the paint. In this combination only the part of described computer etude is concluded. If we remember chess interpretation of the word «etude» – it is solution of the puzzle by composition of the steps.
The second part of the computer etude took already place in Tambov and Katovsk (PVP). (The story will be told from the first person) In Tambov-power I was given the letter for getting paint and varnish productions for 14 millions roubles (of course it was old money) after I turned over our programs. It paid off their debts for electric power. Then I was sent to Kotovsk. At first in the sales department PVP I was refused to give paint bluntly for some strange debts but not real money. But after threat of switching off light and heat they were agreed with difficulty. Paint which suited[4]

the supply department MPEI cost 14 600 roubles for litre and was bottled to the tares (to the drums it is the gist’s slang which I have picked up in Kotovsk). The drum’s volume was 15 and 55 litres. Empty drums cost.  24 and 30 thousand roubles correspondingly. The sales department’s worker of PVP (her name was Olga) making out the waybill on the computer asked what capacities (pardon drums) I would take paint. The flair of old collector of the computer etudes suggested to me that there is typical and main thing real problem of linear programming where we have to maximize the criterion function. This function is the summary volume of paint, the variables are the quantity of full drums of 15 and 55 litres that we had to take and three limitations – (1) paint’s price can not exceed stipulated with Tambour-power 14 million roubles, (2) it is not allowed to take not full jar (it is the limitation to integer numbers) and (3) quantity of the jars different capacity is not allowed to be negative numbers[5]. Olga offered to help me with solving this optimization problem. With help of calculator[6]

she tossed in that I had to take 16 big and 2 small drums containing 910 litres of paint the sum of 13 million 814 thousand roubles. Remembered how I awfully argued in Tambov-power and nevertheless increased the programs’ price from 12 to 14 million roubles I asked Olga if I could not lose 186 thousand i.e. not leave them Tambov-power. She answered negatively and added that she solved such problems seemingly every day optimizing as the paint’s price and its charging to the containers different capacity[7]

and that she knew this problem very well.

Observing «the dance» of Olga’s fingers on the calculator’s buttons and the numbers on it display I understood that Olga uses so-called «Workers’ and Peasants’» and main thing unreliable algorithm of optimization: at first the paint is selected in big tare and then the demand balance (or container’s volume) is filled the paint in little tare. This way we pack a suitcase. At first we put massive things to it and then we put to the empty space all small things. Remembered once more Viona (look the footnote) I asked Olga why she did not use the computer and tabular processor Excel for solving these problems. At this moment there was worker page on the display of her computer. On the spot I offered to show how she could it. In Excel there is Solver which dialogue window is called by the command Find the solution…from menu Service. In this window user shows the cell keeping criterion function which value we have to maximize, the cells with variables of search (at the beginning of optimization they are empty or keeps the values of first approximation to the maximum) and limitations.


The algorithm of optimization with help of Solver Excel may call «lazy»: user forms the table of calculation and says: «I want that you do so that»... the criterion function took maximum (minimum, fixed) values but at that all limitations were realized. For it this is enough to press the button Observe. Solver Excel gave us old result– 16 big and 2 little drums. But I did not want to give it in.

There is good rule: one has to check the solution of the problem up as others methods as the software. Besides we can forget about KISS-principle of programming. It has no connection with kisses although good attitude to the solving problem and to the computer in it we can find.  KISS – is the abbreviation of English phrase: «Keep It Simple, Stupid!» It calls to solve the problem put by simplest method and to use the highly algorithms and methods only when the simple way does not suit because of duration of the calculation or because of irrational use others their resource man and/or computer[8].

The simplest way of solving the problem put by is to sort out all versions and to stop in optimum one. Fortunately there are only 1088 versions: we could not take more than 63 little drums with paint or more than 16 big ones [9]

for our 14 million roubles. The excess can be called  «Computers’ and Workers’ and Peasants’» method of the solution. In addition it can give the total-lot confidence in that the solution is right and that the obtained solution is uniqueness. Even it can show that there are a few such solutions. Such situation does not meet seldom in the integer linear programming problems.

So the excess. Following the rule described above new method of the problem’s solution is necessary to combine with the new software of its realization.  Of course it can be done in Excel by forming the table of all solutions and/or writing the program of the excess in programming language Visual Basic for Applications (VBA), build in Excel. But Olga’s computer had Mathcad too. It quite successfully solves different problems (including economic ones) with out real programming look-up (BASIC, C, Pascal and others.). I had been working at the book for that moment. Reader holds it now in his hands. The example with paint only decorates this book (it is casual pun).

Fig. 6.22. The Fishermen's Problem: 'unprogrammed' Mathcad solution (6_21_fisherman.mcd)

This problem can be solved in Mathcad without resorting to programming. Fig. 6.22 shows how this might be done how by successive manual approximations, with Mathcad just automating the division procedure. We set a first guess at 50 fish and see if the division works; if not, we try 49; and so on, decrementing the guess by one if the division produces a non-integer at any stage. Eventually, we guess at 25 fish, and this proves to be a solution. The first fisherman throws away a fish, and takes eight, leaving 16 (eight each for the others, he thinks). The second (not knowing what the first has done) leaves ten; and the third, six.
This solves the task – but by applying 'manual' work in setting the value of the variable Catch and decrementing the value of the variable Answer. (Note that duplicating the block of operators fixing the actions of the three fishermen, though done for clarity in Fig 6.22, isn't necessary. It's sufficient to decrement Answer
and keep track of Catch).
Let's try to automate the search for a solution to this task.
'1 Initial unstructured BASIC program
Input "Guess"; Answer
label: Catch = Answer
            For Fisherman = 1 To 3
                        Catch = Catch – 1
                        Catch = Catch - Catch / 3
                        If Catch > Int(Catch) Then Answer = Answer - 1: Goto label
            Next
Print
"Answer "; Answer; “fish”
'2. First stage of structuralization: a start
Input
"Guess"; Answer
Answer = Answer + 1 ‘ step backward
label: Answer = Answer - 1 ‘ step forward
            Catch = Answer
            For
Fisherman = 1 To 3
                        Catch = Catch – 1
                        Catch = Catch - Catch / 3
                        If Catch > Int(Catch) Goto label
            Next
Print
"Answer "; Answer; “fish”

'3. Second stage of structuralization: addition of an attribute
Input
"Guess"; Answer
Answer = Answer + 1

label: Answer = Answer – 1

Catch = Answer

            Divided = "yes" ’ indicates catch divided

            For

Fisherman = 1 To 3

                        Catch = Catch – 1

                        Catch = Catch - Catch / 3

                        If Catch > Int(Catch) Then Divided = “no”

            Next

If Divided = “no" Goto label

Print

"Answer "; Answer; “fish”

4. Third step of structuralization: disposal of the label

Input

"Guess"; Answer

Answer = Answer + 1

Do ’ start loop with checking on exit

            Answer = Answer – 1

            Catch = Answer

            Divided = "yes"

            For

Fisherman = 1 To 3

                        Catch = Catch – 1

                        Catch = Catch - Catch / 3

                        If Catch > Int(Catch) Then Divided = “no”

            Next

Loop Until Divided = "yes" ’ end loop

Print

"Answer "; Answer; “fish”

Fig. 6.23. BASIC programs for solving the Fishermen's Problem

Fig. 6.23 shows four BASIC programs to automate the solution of the Fishermen's Problem. In all four, the operator Input requests the first guess (50 fish, for example) and the operator Print gives out the answer: 25 fish.
The first program follows exactly our 'manual' algorithm. Inside the loop for the three fishermen's successive leavings, we watch until we find fractional 'tails': that is, the parameter Catch is not an integer (the built-in BASIC function Int chops off these tails; the Mathcad analogue is the floor
function). Then the guess decrements by one (Answer = Answer - 1) and the program control passes to the labelled statement (Goto label).
Before this program can be translated to Mathcad's programming language, we need to get rid of the label. And not only because in Mathcad's programming arsenal there is no facility to jump to a label, either conditionally or unconditionally, but for other reasons unconnected with Mathcad. In our 'toy' program (item 1 in a Fig. 6.23) the label is quite pertinent and natural, but if a program with labels expands, it becomes difficult to understand and practically impossible to debug and develop. The result, as structural programming wizards rightly emphasise, becomes like spaghetti: try pulling out a block of statements for separate debugging or compilation, and you find adhering strings of Goto links. Besides, such program can't be created by a group of developers ('bottom-up' technology). The first implementations of the Pascal language had no labels at all, as Pascal was developed by Niklaus Wirth for training students in structural programming. The label has appeared only in the late versions. So I think our view on learner programmers and the label must be, "Hide matches from children"!
The first step in structuralizing the BASIC program (see item 2 in Fig. 6.23) is moving the decrement code from the conditional statement to the label. That is:
If Catch > Int (Catch) Then Answer = Answer - 1: Goto

label

becomes

label: Answer = Answer - 1

...

If Catch > Int(Catch) Goto label

There is another necessary change. Rather like an athlete taking a step back before a jump, we must insert Answer = Answer + 1, because when the program is run, label begins by decrementing Answer. Structuralizing generally complicates the algorithm a little: remember that "There's no such thing as a free lunch", "Beauty is only achieved by suffering", and so on.

The second step in structuralizing (see item 3) is extracting the conditional jump from the body of the For loop. For this purpose, we introduce an auxiliary binary variable, Divided, indicating successful or unsuccessful division. Inside the loop, the conditional jump to label is replaced by an "alternative with one shoulder" (that is, Divided stores the result of the binary choice, carrying it to a single exit from the loop – one of the basic structural managing designs). The conditional jump 'slips' down and outside the loop.

After this (see item 4) the program can be modified with one more basic of structural design: a loop with checking on exit, which performs the same function as label and If ... Goto label in item 3. This finally enables the program to completely dispense with labels: the outer loop with exit checking, containing an inner For loop with its 'alternative with one shoulder'.

After all these manipulations, the fourth variant of the BASIC program is the one possible to copy to Mathcad (see Fig. 6.24). It's necessary to define it as a user function, as there are no Input and Print operators in the Mathcad language. Their analogues (the operators [ ]:= [ ] and [ ]=) work, alas, only outside of programs.

Fig. 6.24. Mathcad program for solving the Fishermen's Problem (6_22_fisherman.mcd)

In Fig. 6.24 the result of calling the function Answer are shown for various input values: 50, 24, -3 and even -30 fish. The English physicist and early quantum theorist Paul Dirac postulated not only antiparticles but "antifish". In one version of a well-known story[1], he is remembered as saying that 25 fish was an incorrect solution to this problem, and that the correct answer is -2 fish (or two antifish). If we start with two antifish, throwing away one away gives three antifish; we take our share of one antifish, leaving two antifish .. and so on indefinitely. Our computer solution of the problem shows that even Dirac was mistaken: "Paul, you are not right!" The conditions of the problem are fulfilled by an infinity of numbers – we'll call it a Dirac of fish – with a step of 27 (i.e. -2, 25, 52, etc).
To avoid being an ultra-pedant[2], it's possible to insert at the end of the for loop in Fig. 6.24 a statement break if Divided = "no" to interrupt the loop's operation even before all the fishermen have taken their share. If there aren't three fishermen but more (for example, thirty-three – a task for the reader), this device essentially speeds up the program's operation (see the heading "Optimization of Mathcad programs"). The task can be complicated even more, generalizing to any number of fisherman sharing, or discarding, any number of fish.
The Fishermen's Problem can be solved in another way, by reversing it. Rather than making an initial guess for the catch, we can assume that the last fisherman leaves two fish (it can't be fewer) and increment that number by one until the conditions of the task can be fulfilled. This will solve the problem faster, and we won't ever get solutions of -2 or -29 fish (the paradigm "Keep it simple, stupid!" applies here). It's psychologically difficult for humans to appreciate negative solutions, but the machine does it quietly, without any prejudices. A more thought-out analytical solution of this task – the search for integer roots of one equation with two unknowns – doesn't give the negative answer.
[1]In another version, the story involves shipwrecked sailors dividing a heap of coconuts, the spare coconuts being thrown to a monkey. As the 'Monkey and Coconut Problem', this has been analysed in detail using the number theory of Diophantine equations. For five sailors, the minimum positive number of coconuts is 15621 (Martin Gardner comments that with a Dirac-type solution of four anticoconuts, the monkey benefits most from the process, as it receives a positive coconut at each stage of the division).
[2]There's a Russian word «зануда», meaning "boringly pedantic to the point of irrationality".

не удалось сделать по причинам,

[1] Диск с обучающим курсом вышел — см. рекламу в конце книги.

[2] Этого, увы, не удалось сделать по причинам, описанным в разделе 6.11.

Picture 3.11. The problem about paint

In Mathcad the report of  “ control weighing” you can look at the picture 3.11. Commentaries make clear what takes place in formulas. First of all the function Maximize gave fractional result as we had awaited  (look the point 2) –we can take fraction quantity of big drums so little drums are needless. Remembered epigraph and the title of the etude I had to go to excess of the versions. In Mathcad-document are formed two matrixes with name Оb (point 3.2) and St  (point 3.3). Their elements (there are 1088 elements, i.e. there are 17 columns and 64 lines) keep values of the volume (Оb) and of the worth (St) of paint depending on the combination of the packing. Then (point 3.4) some elements of the matrix Оb are named zero values if the given combinations of the parking do not suit by the worth. The rest is the sleight hand and no mathematics: in point 3.5 number of the line (variable N_15) and of the column (N_55) are determined of the matrix Оb. There is the element with maximum value on their crossing. The reply (6 little and 15 big drums) surprised Olga unpleasantly. She disappointed me unwittingly for 5 litres of paint and for 139 thousand roubles.
The method of searches the coordinates of maximum point that we can see at the picture 3.11 (the double sum) has the considerable limitation: one maximum element has to be in analyzable matrix (in our case it is matrix Ob). If there are a few elements than the reply will be wrong: the sums of the points’ coordinates with the maximum elements will be written to the variables N_15 and N_55. We have observed it in point 2 at the picture 3.9.
So Mathcad has spared me almost 150 thousand roubles. This money is not so great but if you added to them new computer etude, new theme of the lecture and new laboratory work and also the author’s emoluments for this book then the play was worth the candles.
Come back from Tambov to Moscow I analyzed this problem once more on my home computer in a comfortable atmosphere. And there is what I have got.

First of all if we change the initial installation of Solver the problem about paint can be right explained by the Solver of Excel. For it we could not be lazy and had to press the button Parameters… in the dialogue window Search of the

solution. In new dialogue window Parameters of the search of the solution

it was enough to decrease the admissible deviation from 5 to 1%. After it the right solution was found (15 big and 6 small drums). Frankly speaking in Excel Solver is not bad, but its initial installations are. There are few users Excel who apply Solver and press the button Parameters…

But who understand the heart of the problem of the optimization’s installations does not work with Excel. One gets some misunderstandings because of it.

In the second place both Olga and Excel, and Mathcad in different degree were disappointed me a little[10]: 910 litres of the paint could be packed another way-13 small and the same quality big drums[11]. In this case the balance was only 12 thousand roubles. And what is more the solution of the problem about paint with new criterion function (worth of paint in the drums) gives one more result: 37 small and 6 big drums. This way we get one thousand roubles else from Tambov-power.

Version of packing  (quantity of small drums/quantity of big drums)	2/16	6/15	13/13	37/6
Volume of paint (litres)	910	915	910	885
The rest of money (roubles)	186 000	47 000	12 000	11 000

In the third place when I showed this table in the supply department MPEI then I was told that the most optimum alternative both for me (money are important for me) and for MPEI (it needs paint) the fourth one: we get almost all money from Tambov-power. It seems strange but 885 litres of paint is more than 910 and 915. Point is that a lot of paint are lost because of tint from massive drums to small tare. The drum with 15 litres can be taken to the maintainable lecture hall and can be used completely.

The wrong solution is got not only because of bad methods or bad software, but because of user does not know exactly what he really wants. All programs of linear programming’s solutions require the clear formulation of only one criterion function[12]. The purpose is clear when we solve training problems. What purpose do we have for in our life? But it is the mathematics but it is the philosophy…


The excess method illustrated in the picture 3.11 has three own limitations:

1) the variables’ number can not be more than two as soon as in Mathcad there are vectors and matrixes but there are not tensors (three- and so dimensions matrixes)

2) when matrix is excessive dimension the computer refuses to deal with it and it makes a protest as «there is not enough memory»;

3) the calculation (if the excess can be called the calculation) can last to long i.e. for a long time.

Two limitations can be taken off when we go from the method of forming the matrix (the picture 3.11) to the method of excess of the versions. We remember only optimum plan that can be realized by the software. We have done it in our etude number 6 (look at the pictures 6.31 and 6.32).

The excess method turns out indispensable (that is it can not be so unnatural) when the problem is integer but it looses its linearity[13].  In this case traditional methods (for instance the simplex-method) often turn out feeble.

Nevertheless the excess method in Mathcad will be always the misinterpretation of the first water. Mathcad is the program of interpretive type with low speed of realization of initial text. For excess we need not only the compilers but also the compilers optimizing the time of realization the program.

Рассказывают такую историю. Воздушный шар

Рассказывают такую историю. Воздушный шар вырвался из облаков. Летящие увидели на земле человека и закричали: «Где мы находимся?!»  «Вы находитесь в корзине воздушного шара», — таков был ответ. Его дал математик. Только от математика можно услышать совершенно точный и совершенно бесполезный ответ.
Книги, просто информирующие читателя о новых программных продуктах, подобны ответу математика если не своей точностью, то своей бесполезностью. Часто вместе с такой книгой выходит новая версия программы с новыми возможностями, требующая нового анализа (феномен света угасшей звезды). Это одна из причин, почему автор отошел от традиционного описания пакета Mathcad.
С другой стороны, автор понимает, что стиль этюдов (из которых составлена книга) не всегда импонирует читателю издательства «КомпьютерПресс», привыкшему к краткому, четкому и в то же время по возможности полному изложению. Поэтому книга состоит из двух частей.
В первой собраны этюды. Что это такое? На языке музыкантов и шахматистов «этюд» — это небольшое упражнение для отработки некоторых элементов игры. В этюдах этой книги ставится цель не научить желающих работать в программной среде Mathcad (это все равно, что учить плавать вдали от бассейна), а показать идеологию работы с Mathcad. Делается это по возможности на несложных и понятных примерах, затрагивающих актуальные вопросы вычислительной математики (решение уравнений и систем — алгебраических и дифференциальных, оптимизация, статистика, математическое моделирование, техника символьных преобразований, игры и т.д.).
У художников слово «этюд» означает зарисовку, представляющую собой часть будущей большой картины. Математические этюды книги являются не только упражнениями, но и своего рода зарисовками, где внимательный читатель сможет найти немало полезных советов и интересных идей, которые пригодятся ему в дальнейшем при написании больших Mathcad-полотен. Это третья книга автора по информатике в стиле этюдов.
«Старая песня на новый лад» — так можно перевести английское слово «remake». Этот прием особенно популярен в кинематографе. Берется старый фильм, вернее, старый, уже отснятый сценарий, по которому снимается новая версия кинокартины. Технология remake применяется и в программировании, когда, например, DOS-версия какой-либо программы переписывается для Windows. Использовал его и автор: некоторые этюды книги, уже опубликованные, в частности, в журнале «КомпьютерПресс» в виде статей, в книге подвергаются операции remake. В связи с этим автор просит у читателей прощения за возможные повторы и за самокомпиляцию.


У второй части книги (приложение) другой автор и другой стиль: фирма MathSoft, Inc. (101, Main Street, Cambridge, Massachusetts, U.S.A., www.mathsoft.com) предоставила для данной книги справочный материал из Руководства пользователя пакета Mathcad.
Автор выражает глубокую признательность:

Н.А.Сливиной, прекрасному математику и милой женщине — за помощь в подготовке статей, легших в основу книги. Наши с Натальей Александровной дискуссии о месте компьютера в преподавании математики выплеснулись на эти страницы[1].

Игорю Павловичу Боровикову, директору фирмы SoftLine.

Стивену Финчу (Steven Finch) и Робу Дули (Rob Dooly) — сотрудникам фирмы MathSoft, Inc.

Л.Зайцевой, Т.Лоскутовой, Д.Григорян, О.Новиковой, М.Панько, Ю.Бакластову, В.Сабанину, А.Кузьмину, В.Усенко, Ю.Кичатову, А.Очкову, А.Солодову, Е.Шавшиной и всем студентам Московского энергетического института — слушателям курса «Информатика», общение с которыми помогло автору написать данную книгу.

Июнь 1996 г.
[1] И на страницы книги самой Н.А. Сливиной по Mathcad — см. рекламу в конце книги.

и дополненное переиздание двух предыдущих

Форма этой книги двояка.
С одной стороны — это исправленное и дополненное переиздание двух предыдущих книг автора, вышедших в издательстве «КомпьютерПресс» в 1996 («Mathcad PLUS 6.0 для студентов и инженеров») и в 1998 году («Mathcad Pro 7 для студентов и инженеров» — см. далее предисловия к ним). Была даже идея сделать такую обложку книги: в названии не прописывать номер версии Mathcad, а поместить рамку, в которую вставляются таблички c номерами: 6.0 PLUS, Pro 7, Pro 8 и т.д. Так на футбольном поле фиксируются голы.
С другой стороны, автор дополнил книгу новыми примерами и главами, расширяющими представление о Mathcad как об универсальном пакете решения разнообразных задач: чисто математических, физических, экономических и т.д. Описаны возможности Mathcad в формализации нечеткой логики и нечетких множеств, даны приемы структурирования Mathcad-программ, их отладки и оптимизации, детально описан процесс создания с помощью языка C новых встроенных Mathcad-функций и многое другое.
Кроме того:
1. Большое внимание, естественно, уделено новым возможностям «заглавной» версии Mathcad — Mathcad 8 Pro: описана методика и функции решения оптимизационных задач, детализированы более гибкие инструменты поиска корней уравнений и систем, представлена расширенная трехмерная графика и др. Автор тестировал бета-версии программы[1]. Замечания по программе были сообщены разработчикам, а сам диалог автора с фирмой MathSoft в какой-то мере был отображен в этой книге.
2. Существенно изменена форма иллюстраций книги. Теперь это не распечатки Mathcad-документов, а копии экрана дисплея (и даже коллажи нескольких копий[2]) с сообщениями самой системы Mathcad и с комментариями автора, поясняющими те или иные особенности диалога пользователя с компьютером. Операторы с белым фоном прописаны на сером (режим View Region — просмотр областей), что, по мнению автора, также повышает «читабельность» рисунков с задачами книги.
3. Книга получила гриф учебного пособия для студентов математических и инженерных специальностей высших учебных заведений. В связи с этим (скорее для этого) автор дополнил книгу и примеры книги несколько «разжеванными» с методической точки зрения материалами, которые могут показаться лишними для тех, кто уже знаком с компьютером.


4. Данная книга — это не только и не столько книга о программном обеспечении компьютера, но и книга «за жизнь». Автор постарался (ухитрился; насколько удачно — судить читателю) поднять и «околокомпьютерные» и даже «далекооткомпьютерные» проблемы (конфликты современного мира, компьютерное пиратство, налоговая система, компьютер в системе математического образования и т.д. и т.п.).
5. Книга ни в коем случае не «тянет» на всеобъемлющее справочное пособие по пакету Mathcad. В этом автора упрекают некоторые читатели: «Вместо того чтобы просто перевести документацию по Mathcad и опубликовать ее, Вы «гремите» пожарными ведрами и упражняетесь «на купце и сукне». Автор отвечает таким читателям, что «чукча» не переводчик, а «писатель», пардон, «компьютерный писатель» (см. сноску 45 в этюде 7).
6. Автор при работе над этой книгой впервые по-настоящему вкусил плоды Internet: большинство замечаний и пожеланий по предыдущим изданиям книги пришло в электронном виде. Вот три электронных адреса для общения с автором:

электронная почта: ochkov@twt.mpei.ac.ru

персональная страничка автора: http://twt.mpei.ac.ru/ochkov

папка, откуда можно скачать программы книги и другие интересные для читателя файлы: ftp://twt.mpei.ac.ru/ochkov/mathcad

Другие полезные Mathcad-адреса:

сайт фирмы MathSoft, Inc. — разработчика Mathcad: www.mathsoft.com

сайт фирмы SoftLine — российского представителя фирмы MathSoft, Inc. — www.softline.ru

персональная страничка Владимира Павловича Дьяконова, коллеги автора по написанию Mathcad-книг, которому автор безмерно благодарен за советы и поддержку — www.keytown.com/users/Dyak

7. Автор настоятельно просит читателя ознакомиться с предисловиями к двум предыдущим изданиям книги (см. далее), которые также были переработаны и дополнены.
Февраль 1999
[1] Это мог сделать любой пользователь Mathcad, ухитрившийся скачать по адресу beta.mathsoft.com 32-мегабайтную программу. Автор рекомендует заглядывать в это место Internet — вот-вот там появится бета-версия Mathcad 2000!
[2] В одной копии невозможно иметь более одного сообщения об ошибке, более одного диалогового окна, поясняющего нюансы работы пользователя, и т.д.

Поиск корня алгебраического уравнения

Есть хорошее правило: при отладке и испытании программы нужно подсунуть ей задачу, решение которой заранее известно.
На рис. 3.1 с помощью встроенной функции root ищется корень кубического уравнения, записанного в пункте 1. Из графика (пункт 2) анализируемой функции y(x) и из результата работы функции polyroots (пункт 3) видно, что у нее один действительный корень, который легко найти и с помощью функции root, если начальное приближение к корню равно, например, минус 50 (пункт 4).

Mathcad и булевы (логические) функции[25] (English version of text)

В наборе встроенных Mathcad-функций и операторов (см. приложение 2 и 3) нет булевых (логических) функций (Not, And, Or и т.д.), присутствующих во всех языках программирования. А без этих функций не обойтись при решении разного рода логических задач (см., например, задачу о трехсторонней дуэли на рис. 6.36-6.40 в этюде 6), при организации циклов и ветвлений в программах (см. этюд 6) и т.д. Как тут быть и почему разработчики Mathcad не встроили в него эти довольно-таки простые, но такие необходимые функции? Это тем более выглядит странным, если принять во внимание тот факт, что вся цифровая вычислительная техника, на которой, кстати, работает и сам Mathcad, хранит только нули и единицы, а все арифметические и прочие действия – это чистой воды операции булевой алгебры над этими нулями и единицами.
Давайте в этом разберемся.

Черный круг в черном квадрате

Имея под рукой ЭВМ, можно проводить расчеты по алгоритмам, на реализацию которых в докомпьютерную эру решались только одержимые какой-то идеей единицы (своего рода дериваторы). Из литературы известно, что французский естествоиспытатель Бюффон (XVIII век) подбросил монетку 4040 раз и подсчитал, что орел выпал 2048 раз, а решка – 1992. Английский статистик К. Пирсон описал серии бросаний монеты в 12 000 и 24 000 раз. В первом случае орел выпал 6019, а во втором – 12 013 раз.
Тот же Бюффон определил число p очень интересным способом: провел на большом листе бумаги параллельные равноотстоящие прямые линии, стал бросать на него случайным образом иголку длиной, равной шагу между линиями, и подсчитывать общее число бросаний (N) и число попаданий иголки на одну из линий (n). Теория вероятностей подсказывает, что в отношении n/N заложено число p, которое и пытался определить Бюффон столь необычным способом.
Найти, например, значение определенного интеграла методом статистических испытаний (или методом Монте-Карло, так по-другому называют методы расчетов, использованные Бюффоном и Пирсоном) можно следующим образом. Нужно в прямоугольник вписать график интегрируемой функции и бросать в него случайным образом ... камешки. Козьма Прутков в подобной ситуации, но когда камешки бросались в воду, рекомендовал смотреть на круги, ими образуемые; иначе такое занятие будет пустою забавою. Воспользуемся советом, но будем считать не круги, а количество попаданий камешков под график. Отношение числа попаданий (n) к общему числу бросков (N) должно хранить значение интеграла, если верить теории вероятностей.
Итак, бросаем «камешки в воду».

Объем конуса, или Pointiller

От выпускников авиационных вузов часто можно услышать, что они так и не уяснили себе, как железный самолет может летать. Многие финансисты с высшим образованием не понимают (душой не принимают), как могут функционировать безналичные расчеты. Послать деньги в конверте по почте, ну, пусть не золото, а его заменитель (бумажные деньги), – это еще куда ни шло. А вот как деньги могут передаваться по проводам (безналичные расчеты, торговля через Internet и др.) – это уму непостижимо!
Автор в школьные годы очень сомневался в том, что сумма углов треугольника равна 180 градусам. Чтобы развеять сомнения, он (автор) нарисовал чуть ли не тысячу треугольников, измерил транспортиром и просуммировал их углы! Но сомнения все равно остались, благо на то есть основание – неевклидова геометрия.
Очень сомнительно, что объем конуса (а на нем построен целый этюд книги – этюд 2) составляет ровно треть от объема цилиндра, в который этот конус вписан (см. данные из справочника Mathcad на рис. 2.1). Давайте проверим это.

Максимальный объем пожарного ведра

Очень близок к методу Монте-Карло (не только по идеологии, но и по длительности реализации) другой метод, получивший второе дыхание в эпоху компьютеров, – метод перебора. Если задача имеет ограниченное число вариантов ответа, то, не мудрствуя лукаво, можно все их просчитать и выбрать подходящий. Как долго будет длиться такой перебор и как его можно ускорить – ответы на эти вопросы мы дадим в этюде 6.
Наша старая задача о пожарном ведре максимального объема (см. рис. 2.2) может быть решена методом перебора с учетом того факта, что точность раскроя круглой заготовки, равная одному угловому градусу, – предел мастерства даже трезвого жестянщика.

Как автор продавал программы

(английский перевод текста)
Эту главку этюда автор предваряет эпиграфом, но не простым, а специфическим – маленькой программкой.
На рис. 2.9 в этюде 2 мы решали типовую задачу линейного программирования – задачу о плане выпуска стульев. Если цель производства – выпуск максимального количества стульев, то их число определялось правильно: 110+40=150 стульев. Если же целевая функция – общая цена стульев, то ответ был дробный: 18.33 стульев первого типа и 113.33 стульев второго. Как эти цифры округлять и будет ли являться правильным решением округление дробного ответа?

Опять задача старушки «Наири»

Чтобы как-то оправдать метод перебора, вернее, оправдать самого автора книги, ухватившегося за него, вернемся к рис. 3.3 и 3.4. Анализируя тестовые функции, прощупывая их и так и сяк вблизи точки минимума (поверхность, линии уровня), мы согрешили
перебором, но никак не воспользовались плодами этого греха. Исправим ошибку.

ы 2-4. Задачи старушки «Наири»

В специальной литературе приводятся три функции (двухмерная экспоненциальная
функция, функция Розенброка и функция Пауэла), с которых рекомендуется начинать тестирование программных средств поиска минимума. Если программа эту тройку «разъяснит», то... можно проводить следующие испытания. Если же тест закончится неудачей, то... А что, собственно, то? На этот счет нет единого мнения. Одни считают, что такую программу поиска минимума нужно отбраковывать. Другие же полагают, что отдельный промах еще ничего не значит: «Скажи мне, на какой функции твоя программа споткнулась, и я скажу, какой алгоритм в нее заложен и как его можно доработать».
Сейчас мы попытаемся протестировать все три средства поиска минимума, интегрированные в Mathcad, на трех вышеописанных функциях. Испытаниям подвергнется не только пакет Mathcad, но и сам пользователь: любой инструмент сам по себе ничего не значит – работать он может только в умелых руках.
Недостаток всех тестовых функций заключается в… их сущности – в том, что испытующий заранее знает ответ. Экзаменуя программу, пользователь как бы подталкивает ее к ответу, нарушая тем самым чистоту эксперимента.
Но, как мы полагаем, не все наши читатели знают, где три функции:
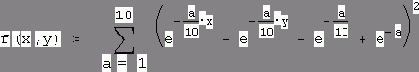 (двухмерная экспоненциальная)
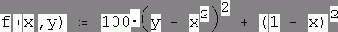            (Розенброка)
                         (Пауэла)
имеют минимумы. Поэтому мы предлагаем читателям сначала попытаться найти их самим. Это будет проверкой не только и не столько пакета Mathcad (а он с тестовой тройкой функций более-менее справился – не смотрите пока на рис. 3.3-3.5), сколько нашего читателя. Тем более что с оптимизацией он уже натренировался «на кошечках» – на ведрах и коробках этюда 2.
(Пауза в чтении книги, связанная с самостоятельной оптимизацией читателями в среде Mathcad тройки тестовых функций ¾ контрольная по этюду 2).

Задача о купце и сукне: решение Удодова-отца I

Рассмотрим рис. 1.1, но сначала немного переиначим Чехова и покажем, как с помощью пакета Mathcad Удодов-отец решил бы задачу о купце и сукне. Внимание! Текст, принадлежащий Чехову, выделен курсивом.
– И без алгебры решить можно, – говорит Удодов, протягивая руку к компьютеру и вздыхая. – Вот извольте видеть
протокол на рис. 1.1.
Он щелкает по клавиатуре компьютера и по мышке, и у него получается 63 и 75, что и нужно было.
– Вот-с... по-нашему, по-неученому.
Если у вас нет под рукой счет (русского калькулятора[1]), к коим Удодов-отец протянул руку, – не беда. Рабочее поле дисплея в среде Mathcad – прекрасный калькулятор: стоит только поставить в конце арифметического выражения знак «=», как машина тотчас и безошибочно выдаст результат вычислений.

Задача об иномарке

На рис. 1.10 помещено решение римейка задачи о гусях – задачи об иномарке: «Спрашивают человека, сколько он отдал за подержанную иномарку, а он отвечает: «Я заплатил за нее столько. Но потом оказалось, что машина не прошла таможенную «очистку». Пришлось заплатить пошлину еще полстолько. Запчастей купил на четверть столько. Одну восьмую столько отдал автослесарям. Одну шестнадцатую столько пришлось выложить в ГАИ за техосмотр (не подмажешь – не поедешь в прямом смысле этого слова). Если сюда накинуть еще 120 долларов, получится цена новой машины ¾ 21200 долларов». Спрашивается, сколько было заплачено за подержанную иномарку?»
Ответ дан на рис. 1.10 ¾ 10 880 долларов.
На рис. 1.10 для компактности сумма разорвана на две половинки, расположенные друг над другом.
Функция root имеет два аргумента: выражение и переменная, найденное значение которой делает выражение равным нулю. Для работы функции root также необходимо первое приближение, вблизи которого ищется корень. Если корней много, то возвращается один – ближайший к первому приближению[10].
Систему уравнений проходится сводить к одному уравнению и решать через функцию root в том случае, если задействовано программирование в среде Mathcad (см. этюд 6). Дело в том, что ключевое слово Given не «запихивается» в программы.
Мы знаем, что если система алгебраических уравнений линейна, то ее лучше решать не конструкцией Given-Find, а с помощью функции lsolve (сравните рис. 1.6 и 1.7). Подобная конкретизация наблюдается и при решении одиночных алгебраических уравнений. Если левая (ненулевая) часть уравнения – это полином n-й степени, то для поиска его корней (всех, включая и комплексные) предназначена встроенная функция polyroots. Ее работа показана на рис. 1.11.

Поиск корней полинома

Функция polyroots (корни полинома) не требует начального приближения, а в качестве аргумента имеет вектор коэффициентов[11]
(они могут быть и комплексными): нулевой элемент вектора ¾ это свободный член, первый¾ коэффициент при x, второй ¾ при х2 и т.д.
На качество работы функции root влияет значение системной переменной TOL. На рис. 1.11 эта переменная по умолчанию была равна 10-3: мы не свели уравнение к тождеству 0 = 0, а сделали так, чтобы правая и левая части по модулю отличались не более чем на 10-3.
Между функциями Find и root наблюдается своеобразный спор. С одной стороны, Find позволяет искать корни как уравнений, так и систем. С этих позиций функция root
как бы не нужна. Но с другой стороны, конструкцию Given-Find невозможно вставить в Mathcad-программы (см. этюд 6). В программах, повторяем, приходится подстановками сводить систему к одному уравнению и использовать функцию root.

Схема балки

Лучше один раз увидеть [схему задачи], чем сто раз услышать [ее условие] – такое «расширение» той же пословицы можно отнести ко всем прикладным программам, работающим под управлением операционной системы Windows, которую не зря называют графической оболочкой. Пакет Mathcad в этом смысле – не исключение. Работая в среде Windows, можно с помощью графического редактора Paintbrush (или какого-то другого) нарисовать схему задачи, а потом через буфер обмена ClipBoard перенести рисунок в окно Mathcad, что и было сделано (рис. 1.12). Если теперь в среде Mathcad подвести к рисунку курсор мыши и два раза щелкнуть по ее левой кнопке, то обрамление рисунка сразу изменится – рисунок перенесется в среду Paintbrush, где его можно доработать, а потом опять вернуть в Mathcad.
В Mathcad-документ можно вставить различные символы из стандартного набора Windows, украшая тем самым задачу (см., например, указательный палец на рис. 6.49 и 6.50). Из этого набора можно подбирать символы и для формирования пользовательских операторов.
Вопреки пословице все же скажем о задаче несколько слов: «Имеется балка, шарнирно закрепленная у левого своего края. В середине она подперта катком. Каток отличается от шарнира тем, что его реакция строго перпендикулярна балке. Справа на балке подвешен груз. Спрашивается: чему равны реакции опор x, y и P, если известен груз G и задана геометрия балки (плечи a, b и угол наклона a[12])?»
Все это словесное описание задачи можно внести в Mathcad-документ ремарками (комментариями), которые подобны ремаркам в тексте пьесы: действующие лица их не произносят, но они помогают лучше понять мысли автора. Пакет Mathcad оборудован текстовым процессором, позволяющим оформить, например, научную статью, не прибегая к специализированным средствам (текстовые процессоры Word, «Лексикон», ChiWriter, Scientific Word и др.). Кроме т ого, буфер обмена ClipBoard поможет перенести фрагменты Mathcad-документа в Word-документ и там дооформить их[13]. Автор хотел написать всю эту книгу в среде Mathcad, но потом от этой идеи отказался из-за проблем макетирования книги.

Итак, решаем задачу о балке. Но сначала два анекдота.

Диалог в учительской:

Преподаватель Закона Божьего, обращаясь к физику: Сегодня ваш любимчик двойку получил. Спросил я его, что такое Божественная Сила. Так он мне ответил, что это произведение Божественной Массы на Божественное Ускорение.

Физик:

Я ему и по физике двойку поставлю. Ведь произведение Божественной Массы на Божественное Ускорение дает Силу с Божественностью в квадрате, а не в первой степени.

Диалог на экзамене:

Преподаватель: Что такое лошадиная сила?

Студент: Это сила, которую развивает лошадь ростом в один метр и весом в один килограмм.

Преподаватель: Да где ж вы такую лошадь видели?!

Студент: А ее так просто не увидишь. Она хранится в Париже, в Палате мер и весов.

Решение любой задачи в любой программной среде, как правило, начинается с ввода исходных данных. Но в нашей задаче о балке присутствует особенность, позволяющая называть Mathcad не просто математическим, а физико-математическим пакетом. Решая физическую задачу (школьную задачу по физике, например), мы часто путаемся не в формулах (все гениальные формулы, описывающие основы мироздания, просты – F=a×m, E=m×c2 и т.д.) и не в расчетах (под рукой персональный компьютер или, на худой конец, калькулятор), а в размерностях. Мало того, что есть различные системы измерений (футы-метры) ¾ в рамках одной системы нет полного единообразия (метры-миллиметры, футы-дюймы и т.д. – см. приложение 7).

Работая с языком BASIC (или с каким-то другим), вводя переменные и задавая им определенный тип, программист больше заботится не о физике решаемой задачи, а о... памяти машины. Тип числовой переменной с точки зрения программиста-прикладника – это атавизм тех времен, когда память машины была одним из лимитирующих факторов при решении задачи: вещественная переменная (8 знаков в мантиссе) занимает вдвое больше места, чем целочисленная, вещественная переменная двойной точности (16 знаков в мантиссе) ¾ вдвое больше, чем вещественная переменная одинарной точности и т.д. Пакет Mathcad в этом отношении расточителен – он присваивает всем числовым переменным двойную точность с 15 знаками в мантиссе. Эти переменные предстают перед глазами пользователя либо в целочисленном (17, например), либо в вещественном (3.14, 107), либо в комплексном (1.84 + 2.2 i) виде[14]. Но через знак «:=» в среде Mathcad можно присвоить переменной не только конкретную величину (20, 1, 2, 30 – математика задачи), но и размерность (ньютон, метр, угловой градус – физика задачи). Что-то подобное есть и в языке BASIC, когда числовая переменная «заглатывает» и свое значение, и свой тип: A = 20%, B = 1&, C = 2.2!, D = 3.3# и Е = 4.4@, опираясь на суффиксы % (простая целочисленная), & (длинная целочисленная), ! (простая вещественная; этот символ обычно опускают, руководствуясь принципом умолчания), # (двойная вещественная) и @ (сверхдлинная целочисленная). Для присваивания величине размерности за ней ставится знак умножения (его можно и не ставить) и вводится название соответствующей размерности (этим мы «баловались» на рис. 1.4). А можно поступить по-другому – нажать на панели часто используемых команд (см. рис. 1.2) кнопку с изображением мерной кружки. После этого на дисплее появится окно со списками физических величин (длина, время, скорость и т.д.) с соответствующими им размерностями (метр, секунда, километр в час и т.д. – см. приложение 6), одну из которых можно вставить в Mathcad-документ.

Мастер размерностей Mathcad

На рис. 1.13 показано, как переменной P присваивается не просто число 20, а двадцать атмосфер. Если потом переменная распечатывается, то по умолчанию выдается «первородная» размерность, которую можно заменить на другую. По умолчанию Mathcad (европейская версия) ориентирован на СИ (SI ¾ Международная система единиц) – см. закладку Unit System в окне Math Options на рис. 1.13. Если это умолчание нарушить и перейти к другой системе (CGS – сантиметр-грамм-секунда или U.S. – британская), то будет и другой ответ, и, естественно, другая размерность давления (см. рис. 1.13). Можно вообще отказаться от конкретных названий единиц и оперировать самими названиями физических величин – см. переключатель Display Dimensions. Названия физических величин при этом можно поменять с английских на национальные: Mass – масса, Length – длина, Time – время и т.д.
В расчете возможны и пользовательские единицы измерения, отсутствующие в списке встроенных:

В среде Mathcad есть атмосфера физическая (atm), но нет атмосферы технической. Фрагмент Mathcad-документа, приведенный выше, исправляет этот недостаток. Кроме того, ради однообразия целесообразно переименовать атмосферы физические. По умолчанию оператор «=» выводит «главную» в системе СИ размерность давления – паскали (Pa), но пользователь может заменить их на другие, в том числе и на пользовательские, введенные ранее.
Можно ввести в расчеты величины, не относящиеся к физическим и отсутствующие в списке встроенных. Мы уже пытались это сделать – см. рис. 1.4. Давайте вернемся к задаче Удодова из рассказа Чехова «Репетитор» и еще раз решим ее в среде Mathcad с новыми условиями:
Купец купил 138 аршин черного и синего сукна, заплатив 250 тысяч старых рублей, 50 новых (деноминированных) и 12 долларов США. Спрашивается, сколько аршин купил он того и другого, если синее (импортное) стоило 25 центов за аршин, а черное (отечественное) ¾ 3 руб.?

Римейк задачи о купце и сукне

Задача вполне реальная: в 1998 году, когда писалась эта книга, к привычным российскому потребителю рублям и долларам добавились деноминированные рубли, сильно усложнившие расчеты[15], подведение балансов и т.д. Двадцать рублей за доллар США ¾ это курс, по которому автор купил себе новый компьютер[16], на котором писалась эта книга.
В среде Mathcad можно сделать ссылку (Reference) на сайт в Internet, где хранятся текущие курсы валют. Тогда наша задача будет совсем реальной.
Пакет Mathcad – это прекрасный автоматизированный справочник, куда следует обращаться не только при решении задач, но и при чтении художественной литературы. Вот отрывок из романа Агаты Кристи «Убийство в Месопотамии»: «Начнем с того, что его рост, на мой взгляд, не превышал пяти футов и пяти дюймов». У Гаршина мы читаем: «Стоял прекрасный июльский день. Прекрасный потому, что было двадцать восемь градусов по Реомюру». А вот другой пример: «От горшка два вершка» – это много или как?! Мы, конечно, понимаем, что это скорее поэтическая, чем метрическая формула. Тем не менее:

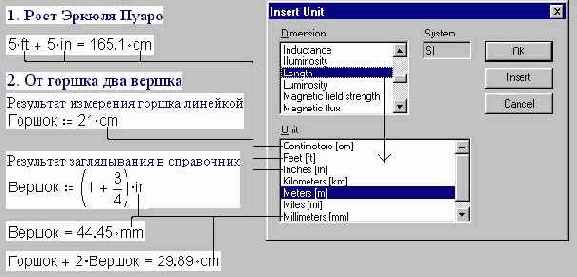
Единицы измерения в среде Mathcad – это своеобразные встроенные символы, к которым применяются простейшие символьные преобразования (о них разговор еще впереди – в этюде 7).
В.М.Гаршин
То, чего не было
В один прекрасный июньский день, – а прекрасный он был потому, что было двадцать восемь градусов по Реомюру…
К константе, выводимой оператором «=», можно добавлять не только название физической величины, но и любую другую переменную, определенную к этому моменту. Вот забавная иллюстрация этого приема: в мультфильме «Тридцать восемь попугаев» Удава измеряют Попугаем, Мартышкой и Слоном. Если задать (подобрать) размеры животных, то Удав «укладывается» в 38 попугаев и еще одно попугайское крылышко, в 5 Мартышек и в 2 Слона. «А в попугаях-то я гораздо длиннее!»:

Но к числовым константам обычно добавляют какие-либо математические
константы: e, ? и др.
Вернемся к задаче о балке. Она сводится к решению системы трех алгебраических уравнений, описывающих равновесия по осям x и y, а также баланс моментов сил[17]
вокруг шарнира. Конструкция Given-Find (дано ¾ найти) использует расчетную методику, основанную на поиске корня вблизи точки начального приближения, заданной пользователем.

Задача о балке: решение I

Глядя на рис. 1.12, можно написать требуемую систему уравнений, «зажав» ее между ключевым словом Given и функцией Find (рис. 1.15). Функция Find возвращает значения переменных, превращающих вышеперечисленные (до слова Given) уравнения в тождества. Если уравнений более одного, то возвращаемые значения размещаются в векторе – в группе переменных, «зажатых в кулак». Но этот «кулак», как мы уже отмечали, легко разжать, выведя на дисплей найденные значения с любой доступной размерностью силы. Но не только этим хороша размерность в задачах. Главное то, что она позволяет автоматически отслеживать «физические» ошибки. Если, к примеру, пользователь сложит секунды с метрами, то Mathcad «заругается» и выдаст протестующее сообщение об ошибке: несовместимые единицы измерения – см. рис. 6.15, заставляющее вспомнить байки о том, как физик подколол лирика (батюшку), а студент озадачил преподавателя (см. выше).
В пункте 0 на рис. 1.15 введены пользовательские единицы измерений физических величин, связанные со встроенными.
Элегантность и простота решения системы уравнений в среде Mathcad, не требующая кодирования алгоритма или поиска соответствующей внешней процедуры, имеет и обратную сторону: у пользователя возникают естественные сомнения в правильности решения. Доверяй, но проверяй! – таким лозунгом можно прокомментировать три нижних выражения на рис. 1.15. Протестировать нужно не только компьютер, но и пользователя: правильно ли он составил исходную систему? Для этого проверяется баланс сил и моментов сил относительно другой системы координат: ось P, ось балки и момент сил вокруг катка. Все верно, идем дальше. Но сначала небольшое отступление.
Из пакета Mathcad в традиционные языки программирования может перекочевать прием, которого им так не хватает. Это задание переменным не только определенного типа (Integer, Long и т.д.), но и размерности: ньютонов, метров, угловых градусов и т.д. Такое расширение понятия переменной позволит оператору Print (если иметь в виду BASIC) выдавать на дисплей ее значение с соответствующей размерностью. Кроме того, вводом размерности можно, как и в среде Mathcad, контролировать правильность написания выражений. Контроль типа переменной в той или иной степени ведется во всех языках программирования. Некоторые версии языка BASIC запрещают писать оператор присвоения Sgn_A! = Dbl_B# + Lng_C&. В последних версиях такого ограничения уже нет. Более того, в Visual Basic введен тип переменных Variant, позволяющий перемешивать даже числовые и литерные переменные: A = "123" + 123, и никакой ошибки.

Ввод размерности в ряде случаев может и должен избавить программиста- прикладника от задания типа переменной. Пусть компилятор сам разбирается, сколько памяти ему отводить под хранение, например, значения угла с принятой в научно-технических расчетах точностью. Число байт под хранение физической величины, как правило, одно и тоже, если использовать «уравнивающие» множители милли, кило, Гига и т.д. В языке BASIC есть зачатки такого автоматического управления памятью компьютера – вспомним цепочку присвоений, когда переменные захватывают и свое значение, и размер памяти, отводимый под их хранение: A = 20%, B = 1&, C = 2.2!, D = 3.3# и Е = 4.4@. В языке программирования, встроенном в Mathcad (см. этюд 6), возможно присваивание переменным размерности (рис. 6.15).
Но нужно помнить, что более-менее сложная система нелинейных уравнений окажется не по зубам не только пакету Mathcad, но и другим мощным пакетам – Mathematica, Maple, Gauss и др. Пакет Mathcad в такой ситуации выдаст сообщение Did not find solution (Решение не найдено), заставляя пользователя поневоле переходить к полуавтоматическому режиму – менять значения начального приближения и (или) величину точности TOL (TOLerance – точность, погрешность), а также метод поиска решения (Mathcad 8) – рис. 1.8. Функция Find решает систему так, чтобы левые и правые части входящих в нее уравнений отличались на величину, не превышающую значения TOL[18]. Это предопределенная (системная) переменная среды Mathcad, хранящая по умолчанию значение 0.001, которое можно изменить, записав в Mathcad-документе выражение TOL:=0.0000001, например. Но и это часто не помогает. В коллекции автора (химика по специальности) есть Mathcad-задача поиска значения pH (водородного показателя) буферного водного раствора, сводящаяся к решению системы из восьми нелинейных алгебраических уравнений. Так вот, только при строго определенных начальных условиях пакет Mathcad находит правильное решение. Шаг влево, шаг вправо – расстрел: малейший отход от начальных условий, и слово Find «обливается кровью» и появляется соответствующее сообщение об ошибке. Но эта же задача в неограниченном диапазоне исходных данных прекрасно решается последовательными приближениями с поиском в цикле корня одного-единственного уравнения. Отход от лобовой атаки (от использования конструкции Given-Find) возможен лишь в том случае, если система уравнений не абстрактная, какие обычно приводятся в задачниках по математике, а реальная, отображающая конкретную прикладную (физическую, химическую, биологическую и т.д.) задачу. Кроме того, прикладник (физик, химик, биолог и т.д.), решая задачу, может сделать разумные допущения, линеаризирующие, например, некоторые выражения или уменьшающие их число. Другое важное преимущество метода последовательных приближений состоит в том, что прикладник, зная физику задачи, может менять точность расчетов при обработке выражений, входящих в систему. В блоке же Given-Find, как было уже отмечено, это недопустимо. В нем можно лишь смягчить эту проблему с другого конца – ввести в выражения балластные (нормирующие) коэффициенты, уравнивающие их по отношению друг к другу и позволяющие им решаться с одной точностью. А это опять же потеря физики в угоду математике. Но тем не менее все перечисленные ухищрения часто остаются тщетными из-за того, что система просто... не имеет решения, да и вся задача ориентирована не на поиск корней, а на минимизацию некоторых величин. В этом случае функция Find заменяется на функцию Minerr (MINimal ERRor). С помощью блока Given-Minerr можно решать обширный класс оптимизационных задач, о чем мы еще поговорим в этюдах 2 и 3.


А вот еще одна перефразировка: на компьютер надейся, а сам не плошай!
В том смысле не плошай, что немного подумай и подскажи компьютеру, как быстрее и точнее решить задачу. Высший компьютерный «пилотаж» помогает пользователю обходить неизбежные ошибки и неточности программной среды.
Более глубокий анализ равновесия балки позволяет описать его системой линейных алгебраических уравнений. А для решения такой задачи в пакете Mathcad есть особые инструменты – операторы и функции работы с матрицами и векторами, которые уже были использованы нами при решении задачи о купце и сукне (см. рис. 1.7). Но, решая задачу о балке поиском корня системы линейных алгебраических уравнений с коэффициентами при неизвестных, хранящихся в квадратной матрице A (см. рис. 1.16), и со свободными членами, хранящимися в векторе B, от единиц измерения приходится отказываться (пункт 1). Это потому, что элементы матриц и векторов в среде Mathcad должны либо иметь одинаковую размерность, либо быть безразмерными. А это не просто ошибка пакета, а общая методологическая ошибка: элементы матрицы должны иметь разнородные размерности.
Матрица и вектор пакета Mathcad имеют «родственников» на языке BASIC – двухмерный и одномерный массивы (см. рис. 1.7). Массив же – это объединение сугубо однотипных величин. Разнотипные переменные объединяются в запись. Массив, образно говоря, – это бутылки в ящике, а запись – бутылки в баре. Чтобы примирить физику с математикой, достаточно разрешить в столбцах матрицы помещать величины с разнородными единицами измерений, считая матрицу не только двухмерным массивом простых переменных, но и одномерным массивом векторов. В записи (в векторе) могут, конечно, храниться и однотипные переменные – переменные с одной размерностью или вообще лишенные ее. Аналог одномерного массива в Mathcad – это матрица с одной строкой (вектор-строка). Но такая «горизонтальная» матрица не выражается через переменную с нижним индексом. Переменная с индексом – это нормальный, «вертикальный» вектор (вектор-столбец). Если допустить, что матрица – собрание (множество) величин с различной размерностью, то тогда придется все матричные операторы и функции разделить на группы по отношению к единицам измерений. Так, функции min (поиск минимального элемента в массиве) и max (поиск максимального элемента в массиве) не могут допустить неодинаковых размерностей в элементах матрицы-аргумента. Оператор же определения детерминанта должен преобразовывать матрицу как массив векторов. Величины в строках здесь должны быть одной размерности.

Задача о балке: решение II

С точки зрения математика (несмотря на отсутствие размерности, что влечет за собой смысловую потерю физики задачи) решение в среде Mathcad системы линейных алгебраических уравнений через матрицы (см. пункт 4 на рис. 1.16) более удобно, чем через блок Given-Find (рис. 1.15): отпадает необходимость в начальном приближении (у линейной системы не более одного корня-вектора). Кроме того, матричное решение задачи, как правило, точнее (сравните пункты 5 на рис. 1.15 и 1.16): равновесие по оси P на рис. 1.16 имеет абсолютную точность.
Есть и другие причины, по которым приходится отказываться от размерностей. Международная система единиц (СИ) базируется на семи основных единицах (длина – метр, масса – килограмм, время – секунда, сила электрического тока – ампер, термодинамическая температура – кельвин, сила света – кандела и количество вещества – моль). Нам для решения простейшей задачи с размерностями на рис. 1.14 пришлось вводить дополнительную размерность (руб), воспользовавшись тем, что в данном расчете нет ссылки на время (принцип «Время ¾ деньги»). Это один из примеров того, почему с единицами измерений при работе в среде Mathcad часто приходится расставаться. Вина здесь не только фирмы MathSoft, но и всей теории размерностей. Дело в том, что эта теория какая-то незаконченная: недаром математические справочники избегают ее освещения. В физических же справочниках, когда дело доходит до размерностей, теряется всякая логика. Из-за этого многие научные дисциплины стараются избавиться от пут размерностей, вводя безразмерные величины (критерии): число Рейнольдса, например, если вспомнить аэродинамику. Освобождение от размерностей подкреплено целой теорией ¾ теорией подобия. Все это не могло не отразиться на развитии пакета Mathcad: упомянутая семерка размерностей (масса, длина, время, заряд, температура, сила света и количество вещества) неудобоварима в психологическом и даже в парапсихологическом смысле. Сама по себе размерность – понятие скользкое, опирающееся не только на науку, но и на привычки людей, законы искусства и даже на постулаты религии[19]. Стоит только вспомнить попытки заменить в метеосводках миллиметры ртутного столба на гектопаскали. Парапсихологический, если так можно выразиться, аспект проблемы размерностей в среде Mathcad выражается в том, что размерность там должна быть не та, которая заложена в Международную систему и в Mathcad 7 и 8.

Семь – число совершенное и в науке, и в искусстве, и в религии: стоит только вспомнить цвета радуги, ноты музыкальной гаммы, дни недели, чудеса света, наиболее промышленно развитые страны мира, античных мудрецов, смертные грехи... В классическом варианте языка BASIC имеется семь структурных управляющих конструкций алгоритма (цикл с предпроверкой, цикл с постпроверкой, цикл с выходом из середины, альтернатива, функция, процедура и множественное ветвление) и семь типов переменных (Integer, Long Integer, Single-precision Floating Point, Double-precision Floating Point, Currency, String и Туре – тип, заданный пользователем). Да и сама цифровая вычислительная техника базируется не на числе 8 (байт), как принято считать, а на числе 7. Два (бита) в степени восемь (256) – это число символов в ASCII-таблице. Но ASCII-таблица ни машиной, ни человеком никогда не воспринимается как единое целое, а всегда разбивается на две половины – верхнюю и нижнюю по 128 знаков в каждой. А это два в степени семь, а не восемь:
Тьмы низких истин нам дороже
Нас возвышающий обман.
А. Пушкин
В Международной системе семь единиц не потому, что это правильно, а потому, что это красиво.
Еще одна базовая размерность лежит на поверхности, но почему-то напрочь отвергается учеными. Это единица измерения стоимости – рубли, доллары, марки и т.д. (см. рис. 1.4 и 1.14). Тот же физик (вспомним два анекдота) может сказать: У меня в кабинете лежит книга массой в один килограмм, толщиной в один сантиметр и ценой в тысячу рублей, но в физико-математические дисциплины и пакеты единица измерения стоимости никогда не будет введена. Из-за этого в среде Mathcad экономические расчеты лишены размерности (в Mathcad-документах на рис. 1.4 и 1.14 мы этот недостаток попытались обойти). Кстати, в язык BASIC размерность валюты введена косвенно через новый тип числовых переменных – Currency.
Можно предположить, что еще какая-то базовая размерность, объединяющая килограммы, метры, секунды, кулоны (амперы) и градусы Кельвина с чисто эмпирическими (кандела) или счетными (моль) единицами, пока неведома нам, но зарезервирована Создателем (Господом Богом


или Природой – кто как для себя считает) для измерения биополей, например, или чего-то другого, относящегося к областям экстрасенсорики, телепатии, телекинеза и прочей чертовщины. Говорят, что в Солнечной системе более десяти планет. Где-то там, за солнечной «околицей», описывает свою дугу неведомая планета, о существовании которой мы можем судить только по вносимым ею возмущениям в траектории движения Нептуна или Плутона. Так и седьмая гипотетическая основная единица измерения, витая в областях, пока недоступных научному анализу, вносит психологические (парапсихологические) возмущения в теорию размерностей. Это не могло не отразиться на пакете Mathcad, пользователи которого, «наигравшись» с размерностями, в конце концов от них отказываются не только по психологическим причинам (вводим радианы или градусы, например, а угол все равно остается безразмерным), но и из-за фактических ошибок, вину за которые нельзя возложить только на разработчиков пакета Mathcad, если принять во внимание «парапсихологические возмущения».

Декартов график (X-Y Plot)

На рис. 1.17 помещен самый распространенный график: декартов график (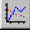 – X-Y Plot), иллюстрирующий связи между двумя (одна кривая на графике) или несколькими (две или более кривых) векторами. На оси ординат графика можно было бы написать не a, а a, a, a, отмечая тем самым связь линий с парами векторов x-a, y-a и P-a. Но по умолчанию (которое нередко находится в противоречии с пониманием) мы пишем только одну букву a.
Первый вектор[20]
(у нас это значение угла наклона балки a) будет аргументом. Второй, третий и последующие векторы (реакции опор x, y и P) могут в явном виде и не присутствовать – их значения вычисляются через функциональные зависимости пункта 2 на рис. 1.17 во время построения графика. Повторяем ¾ на оси аргумента графика на рис. 1.17, если быть до конца педантичным, следует писать a, a, a, помечая тем самым пары векторов, отображаемых на графике.
Декартов график строится, как правило, в три шага:

шаг 1: задание вида функций одной переменной; они у нас уже есть – x(a), y(a) и P(a);

шаг 2: формирование вектора значений аргумента; у нас он меняется от нуля до 360 градусов с шагом 5 угловых градусов[21];

шаг 3: построение графика.

Третий шаг, в свою очередь, состоит опять же из трех шагов;

шаг 1: рисование на экране дисплея заготовки графика – прямоугольника с черными квадратиками у левой и нижней сторон; заготовка графика появляется в отмеченном курсором месте после того, как пользователь нажмет на одну из кнопок панели инструментов Graph или выберет соответствующую команду в меню Insert;

шаг 2: заполнение пользователем двух черных квадратиков заготовки графика («вакантных мест») именем функции (или вектора) и именем аргумента. Если функций больше одной, то их имена вводятся через запятую. В заготовке есть и другие черные квадратики, которые можно не заполнять. Среда Mathcad, например, сама рассчитает диапазон изменения Y. График появляется на дисплее после вывода курсора из зоны графика (автоматический режим расчетов) или после нажатия клавиши F9 (ручной или автоматический режим расчетов). Параметры графика задаются стандартными по умолчанию;

шаг 3 необходим, если параметры графика, установленные по умолчанию на предыдущем шаге, пользователя не устраивают и он хочет их изменить, вызвав соответствующее диалоговое окно (см. например, рис. 1.19 и рис. 3.12). Размеры графика изменяются обычной протяжкой, принятой в среде Windows.

В среде Mathcad 7 и 8 допустима быстрая (двухшаговая) технология построения графика (QuickPlot): пользователь набирает функцию (sin(x), например) и сразу отдает команду построения декартова или иного графика. Все! График будет построен с разбросом аргумента от минус 10 до плюс 10 и с пятьюдесятью точками внутри. Если это пользователя не устраивает, то график форматируется.

Параметрический декартов график (продолжение рис. 1.17)

На рис. 1.18 показан так называемый параметрический декартов график – взаиморасположение двух векторов в зависимости от значения третьего параметра (у нас это угол наклона балки). В этом графике физический смысл узреть довольно сложно (влияние реакции катка, подпирающего балку, на x-реакцию шарнира, с помощью которого балка прикреплена к стене), но красота его бесспорна – подобно лемнискате Бернулли или бабочке для смокинга.

Полярный график (Polar Plot – продолжение рис. 1.17)

Если аргумент представляет собой угол, изменяющийся от 0 до 360 градусов, а значения функции x(a), y(a) и P(a) имеют период, как в нашей задаче о балке, то ось аргумента декартова
графика целесообразно «свернуть в круг» и получить полярный график ( – Polar Plot – рис. 1.19).

Экран дисплея при работе в среде Mathcad 8 Pro

Пустой Mathcad-документ – это волшебный лист бумаги, на котором пользователь с помощью клавиатуры и мыши может писать математические выражения в виде, принятом научным миром задолго до появления компьютера. В этом одна из причин популярности Mathcad.
Создать математические выражения помогают специальные панели (палитры) кнопок:

проиллюстрирована работа Мастера трехмерных

На рис. 1. 20 проиллюстрирована работа Мастера трехмерных диаграмм, введенного в Mathcad 8. Он существенно помогает строить графики и диаграммы, показанные ниже: пользователь по шагам строит график (кнопка «Далее»), откатываясь при необходимости назад («Назад»).

График поверхности (Surface Plot – продолжение рис. 1.20)

На рис. 1.21 графически отображается функция уже не одного, а двух аргументов – правого плеча балки b и угла ее наклона. График поверхности ( – Surface Plot), как правило, строится не в три (см. выше), а в семь шагов (тоже красиво).

шаг 1: задание вида функций двух переменных; она у нас уже есть – x(b, a) ¾ см. пункт 5 на рис. 1.20;

шаг 2: нумерация узлов сетки-поверхности по первому аргументу – i := 0.. 40;

шаг 3: формирование вектора первого аргумента – bi := -5 × м + 0.25 × м × j (м – это метры);

шаг 4: нумерация узлов сетки-поверхности по второму аргументу j := 0.. 40;

шаг 5: формирование вектора второго аргумента – aj := 9 × ° × j (° – это угловые градусы);

шаг 6: заполнение матрицы (у нас она носит имя M) значениями функции x(b, a) в узлах сетки;

шаг 7: построение и форматирование графика поверхности.

Такая последовательность построения поверхности рекомендована в документации Mathcad. Но читатель может познакомиться и с другими, более удобными методиками: рис. 3.3 – задание координат углов сетки поверхности и рис. 3.4. – задание центра квадрата сетки.
Наша сетка (здесь она квадратная с количеством узлов 41 на 41) как бы превращается в гамак: – ее узлы поднимаются над нулевой отметкой пропорционально значению двухмерной функции. Форматирование графика сводится к вращению этого «гамака» относительно наблюдателя, к заливке ячеек разным цветом, к построению координатной сетки, к освещению этой ажурной конструкции из разных точек и др. Здесь особыми возможностями обладает Mathcad 8.

Карта линий уровня (Contour Plot – продолжение рис. 1.20)

Очень часто, особенно при поиске оптимумов функции двух переменных (см. этюды 2 и 3), полезнее просмотреть не график поверхности (рис. 1.21), а карту линий уровня ( – Contour Plot – рис. 1.22), которые подобны линиям на физической географической карте, охватывающим горы и впадины (максимумы и минимумы). Если области графика залить цветом[22], то сходство с картой будет полное. В среде Mathcad 8 есть различные палитры раскраски трехмерных графиков: rainbow (радуга – самые верхние точки красные, а самые нижние – фиолетовые), topographic (топографическая – высшие точки белые, покрытые вечными снегами), gray (оттенки серого как в этой, увы, не цветной книге) и др.

Векторное поле (Vector Field Plot – продолжение рис. 1.20)

Вместо линий графика на рис. 1.22 можно поставить маленькие стрелочки, отмечающие направление изменения функции двух переменных. Тогда получится векторное поле ( – Vector Field Plot – рис. 1.23). Возвращаясь к географической карте, можно сказать, что маленькие векторы отмечают направления течения рек и ручьев[23]. Этот график очень полезен, например, при решении дифференциальных уравнений (см. этюд 5) – с его помощью довольно просто нарисовать семейство кривых – решений уравнения.

Трехмерный точечный график (3D Scatter Plot)

Гибридом декартова графика (рис. 1.17 и 1.18) и графика поверхности (рис. 1.21) является так называемый трехмерный точечный график ( – 3D Scatter Plot – рис. 1.24). Его главное отличие от графиков, отображающих прямоугольные матрицы (рис. 1.21-1.23), состоит в том, что с его помощью можно изобразить пространственную взаимосвязь не двух, а трех векторов (x, y и P, например). С помощью трехмерного точечного графика можно визуализировать и матрицу.

Трехмерная столбчатая диаграмма (3D Bar Chart)

Элементы матрицы (или вектора) можно уподобить столбикам, расставить их на плоской поверхности двух аргументов и получить трехмерную столбчатую диаграмму ( – 3D Bar Chart). На рис. 1.25 аргумент один. Подобный, но плоский график можно построить и в декартовых координатах (см. рис. 5.1).
О графических возможностях пакета Mathcad можно написать целую книгу (что входит в перспективные планы автора). Мы же отсылаем читателя к приложению 1, где перечислены некоторые команды настройки графиков. Видов графиков, как уже было отмечено, семь, а инструментов работы с ними – три. Первый инструмент – это форматирование графика. Объемные графики (вернее, псевдообъемные – видимость объема имитируется на все том же плоском дисплее) – это скорее способ украшения
документов, а не средство научного анализа. Настоящая работа ведется с плоскими (двухмерными) графиками. Для них в среде Mathcad припасены два других инструмента: лупа (Zoom – рис. 1.26) и трассировка (Trace – рис. 1.27).

Лупа (Zoom) графиков

Если человеку необходимо более подробно рассмотреть какой-либо объект, он берет в руки лупу ¾ она и изображена на одной из кнопок панели Graph (см. рис. 1.26). Нажав на эту кнопку, пользователь вызывает диалоговое окно X-Y Zoom с четырьмя полями и пятью кнопками. Протяжкой на рассматриваемом графике можно выделить прямоугольную область (см. рис. 1.26), отмеченную пунктиром. Координаты области отображаются в диалоговом окне X-Y Zoom. Нажатием кнопки Zoom эту выделенную область можно увеличить до размеров исходного графика ¾ и таким образом под лупой рассмотреть левый корень системы уравнений, решаемой на рис. 1.8. Можно все вернуть в исходное положение (кнопка Unzoom), выбрать новую область и раскрыть ее окончательно (Full View).

Трассировка (Trace) графиков

На график можно посмотреть как бы через прицел снайперской винтовки, если нажать на последнюю, девятую кнопку графической панели (рис. 1.27), появится диалоговое окно X-Y Trace. Если после этого курсором мыши прощупывать кривую на графике, то появятся два волоска (crosshair), координаты пересечения которых отображаются в окне Trace. Эти координаты можно скопировать (CopyX и CopyY) в буфер обмена, а потом перенести в Mathcad-документ и использовать в качестве первого приближения при поиске корня системы уравнений.
Естественно, семь графиков далеко не всегда могут удовлетворить потребности и фантазию пользователя. Разработчики Mathcad не стали утяжелять пакет «экзотической» графикой, а создали новый пакет Axum, предназначенный для более тонкой и изощренной визуализации данных из среды Mathcad. Кроме того, данные из Mathcad-документа с помощью инструмента MathConnex (см. приложение 7) можно перенести в среду Excel или MatLab и там воспользоваться графическими возможностями этих пакетов.

Мастер функций Mathcad

Встроенные операторы вводятся через нажатие кнопок с их изображением – см. рис. 1.3.
Функции (встроенные и пользовательские) с одним или двумя аргументами можно вводить в Mathcad-документ через нажатие кнопок «fx», «xf», «xfy» и «xfy» (нижний ряд на панели Evaluation на рис. 1.3). При этом появляются заготовки постфиксного
и префиксного операторов с одним операндом («fx» и «xf» – первый из них и был задействован на рис. 1.16), инфиксного «xfy» и древовидного «xfy» операторов с двумя операндами. Древовидный вызов оператора хорошо проиллюстрирован на рис. 3.14 в этюде 3.
Встроенные операторы отличаются от встроенных функций (не только в среде Mathcad, но и в программировании), во-первых, тем, что функции все равны между собой, оператор же умножения «главнее» оператора сложения: 2+2*2 равно шести, а не восьми. Кроме того, в среде Mathcad встроенную функцию с одним или двумя аргументами можно непосредственно вызвать в виде оператора (a sin, например). Со встроенными операторами не все так просто. На рис 1.29 даны иллюстрации работы функций и операторов в среде Mathcad.

Операторы и функции

Второе отличие функции от оператора в среде Mathcad в том, что оператор имеет фиксированное количество операндов: один (n! – факториал, например), два (сложение, вычитание, степень, дифференциал, неопределенный интеграл), три (сумма и произведение элементов вектора, производная высокого порядка и др.), четыре (сумма и произведение ряда, определенный интеграл (см. выше) и т.д.).
Некоторые же функции (Find, MinErr, Minimize, Maximize, например) способны иметь дело с переменным числом аргументов. Третье отличие функции от оператора в среде Mathcad в том, что встроенную функцию можно переопределить. Если, например, пользователя не устраивает то, что аргумент синуса должен быть в радианах, он может заставить синус «глотать» угловые градусы (рис. 1.29).
Внешне для пользователя функция отличается от оператора тем, что у функции есть имя (это обычно слово или сокращение слова), а у оператора – символ. Правда, некоторые операторы вообще не имеют ни имени, ни символа: xy (x в степени y) и Vi (i-й элемент вектора V). Функций-анонимов в среде Mathcad нет.
Пара операторов Mathcad может иметь один и тот же символ, но прописанный разным стилем: сравните светлое равно (вывод числового значения) и полужирное равно (булево равенство). В среде Mathcad можно оперировать одноименными переменными и функциями пользователя с различным шрифтом, с помощью которого отмечаются совершенно различные переменные и функции. Так, в расчете основные переменные можно прописать шрифтом размером 14, а вспомогательные – 10. Традиционные языки программирования такого «безобразия» не допускают.
Одна из причин популярности Mathcad заключается в том, что пользователь вправе вставлять в документы либо функцию, либо оператор в зависимости от того, к чему он привык, изучая математику в школе или в институте. Благодаря этому Mathcad-документ максимально похож на лист с математическими выкладками, написанными от руки или созданными в среде какого-либо текстового процессора (Scientific Word, ChiWriter и др.).

А вот вторая причина успеха. Традиционное программирование разводит во времени процесс решения задачи на три независимых этапа: программа пишется, затем отлаживается

и оптимизируется. В среде Mathcad эти процессы слиты воедино: вводя новую формулу в документ, можно не только посмотреть результат вычислений по ней, но и построить график, создать анимационный клип и т.д.

В среде Mathcad 7 и 8 операторы «:=» (ввод значения) и «=» (вывод значения) несколько перепутались. Если пользователь забудет, что переменная А, например, не определена, и наберет на клавиатуре «A=», то оператор вывода «=» автоматически превратится в оператор присваивания «:=» (технология SmartOperator – сообразительный оператор). Вот хорошее правило: никогда не используйте оператор «:=» для ввода значения переменной. Для этого нужно использовать оператор «=». Это убережет от случайного переопределения «занятой» переменной – как пользовательской, так и встроенной. Переменная А, например, – это один ампер.

Создавая пользовательский оператор, ему можно давать не только имя, но и символ, незанятый встроенными операторами. В конце рис. 1.29 показана технология создания булевого оператора «примерно равно», доводящего до семи (опять семь!) список операторов сравнения вещественных величин («равно», «неравно», «больше», «меньше», «больше или равно» и «меньше или равно» – см. соответствующие кнопки на панели Evaluation на рис. 1.3 и 1.29). Символ «»» берется из таблицы символов Windows (Alt+0196) или из таблицы символов самого Mathcad (см. ниже), которая вызывается из Центра Ресурсов. Здесь это уже не общая переменная (с шрифтом Arial Cyr), а переменная первого пользователя (User1 со шрифтом Symbol). На рис. 1.15 по такой же технологии введена пользовательская единица измерений – угловой градус (°).



Кроме того, диалог пользователя с компьютером в средах Mathcad 7 и 8 обогащен текстовыми переменными. Для их поддержки введены «текстовые» функции. Их работа показана в пункте 1 на рис. 1.30.

Панели математических инструментов Mathcad 8 Pro

Нажав на кнопку «=» (пальцем на клавиатуре или мышкой на панели Arithmetic – см. рис. 1.3), пользователь получит на пустом месте экрана дисплея (в Mathcad-документе) заготовку оператора вывода числового значения.
- = - -
В левый пустой квадратик (placeholder, «держатель места») записывается выражение, численное значение которого появится во втором (среднем) квадратике, если увести курсор (автоматический режим расчета, включенный по умолчанию после запуска Mathcad, – см. слово AUTO внизу рис. 1.2) или нажать F9 (автоматический и/или ручной режимы). В правый квадратик можно записать нужную размерность, если обсчитывается какая-либо физическая величина. Если величина безразмерная, а пользователь все-таки вставит в правый квадрат букву m (метры), например, то Mathcad ругаться не будет, а превратит m в m × m-1, то есть в ничто. Как правило, показанной выше заготовки пользователь не видит, а просто нажимает «=» после набора математического выражения (см. рис. 1.1). Кнопка «=», повторяем, есть и на клавиатуре вверху справа. Нажимать можно и ее. Таким же образом продублированы и основные арифметические действия: сложение, вычитание, умножение, деление – на панели Arithmetic есть и цифры 1, 2, 3 и т.д. Считать в среде Mathcad можно, не касаясь клавиатуры, а только двигая мышку и щелкая по ее кнопкам.
Mathcad-документ на рис. 1.1 – это почти одни комментарии. Комментарии записываются в прямоугольную область, которую можно вставить в любом свободном месте Mathcad-документа: например, выше комментируемого выражения (рис. 1.1) левее или правее него (см. тексты BASIC-программ на рис. 1.7). Комментарии, как правило, имеют шрифт, отличный от шрифта переменных и констант[2]. Кроме того, на дисплее комментарии выделяются цветом. По умолчанию фон экрана белый, цвет выражений – черный, а цвет комментариев – синий. Но пользователь вправе поменять эту палитру, приспособив ее под свои особенности цветового восприятия. На рис. 1.1 белый фон только у областей комментариев и формул, остальное залито серым цветом. Это достигается переключателем Regions (регионы, области) в меню View (просмотр). Пользователям Mathcad, особенно начинающим, полезно работать в этом режиме, так как он позволяет четко фиксировать границы областей формул и комментариев. По умолчанию весь фон документа белый (белый лист бумаги!). Кроме того, на некоторых рисунках книги показаны панели, кнопки которых помогают создавать Mathcad-документ и решать поставленные задачи, а также другие ремарки автора и сообщения Mathcad.
По умолчанию, нажимая кнопки, пользователь вводит математические выражения (пишет черным по белому). Ввод комментария предваряется нажатием на клавишу «”» клавиатуры. Можно поступить и по-другому – набрать, например, букву С, а потом нажать на клавишу пробела: переменная С превратится в первую букву комментария (автоматически поменяет свой цвет с черного на синий, а шрифт – со шрифта переменных на шрифт комментариев).
Для вычислений можно использовать не только оператор «=», но и оператор «®» – оператор вывода не числового, а
символьного значения. О нем подробно будет рассказано в этюде 7. Здесь же на рис. 1.4 показано, как оператор «®» позволяет имитировать (пока только имитировать – см. главку 1.2) размерности физических и финансовых величин.

Работа текстовых функций

Между числовыми и текстовыми переменными нет глубокого водораздела. Это проиллюстрировано в пункте 2 на рис. 1.30, где моделируется бросание монетки: орел – это 1, а решка – это решка. Переменная a принимает то числовое, то текстовое значение. Об этом мы еще поговорим в этюде 6 (рис. 6.46 и 6.47). В связи с этим в среду Mathcad 8 введены специальные булевы функции, возвращающие 0 или 1 – в зависимости от типа аргумента (см. пункт 4 на рис. 1.30).
[1] Покойная матушка автора умела вычислять на счетах квадратный корень.
[2]
На рисунках книги шрифт переменных и констант Arial Cyr (см. рис. 1.29), а шрифт комментариев – Times New Roman Cyr.
[3]
Там может быть и оператор, например Vi или M, локализующий элемент массива (V) или матрица (M), куда заносится соответствующее значение.
[4]
Проблему русских имен переменных в среде Mathcad мы рассмотрим в главе 6 при раскладке пасьянса.
[5]
Между Given и Find могут быть записаны и неравенства. Но об этом позже.
[6]
Элементом вектора (матрицы) может быть новый вектор (матрица). В этом случае говорят о вложенном массиве (nested arrays).
[7] В математике принято говорить «элемент матрицы» и «компонента вектора», а не «элемент вектора». Но мы будем применять второй термин, так как в среде Mathcad нет принципиальной разницы между вектором и матрицей: вектор ¾ это матрица с одним столбцом.
[8]
Если при создании матрицы нажимать не OK, а Insert, то окно работы с матрицами будет оставаться на экране дисплея.
[9] В разработке функций, предназначенных для решения алгебраических уравнений и систем (Find, MinErr и др.) принимала участие и фирма Frontline System, Inc. (см. конец приложения 1 с указанием авторских прав). Эта же фирма поставила Решатель (Solver) для электронных таблиц Excel.
[10]
Это не совсем так, вернее совсем не так – см. начало этюда 3.
[11]
Символьная математика Mathcad умеет не только выяснять, является ли выражение полиномом или нет, но и вычисляет коэффициенты полинома (см. этюд 7).

[12] В Mathcad- документ греческие буквы вставляются нажатием кнопок специальной панели (ab – см. рис. 1.3). Другой способ ввода греческих букв – аккорды: Ctrl + p дает ? и т.д.

[13] В шестой версии Mathcad в меню File появилась команда Export Worksheet, существенно облегчающая эту работу. В седьмой и восьмой версиях этой функцией нагружена команда Save as... Кроме того, Mathcad-документ можно внедрить в Word-документ (и наоборот), используя технологию OLE. В среде Word, например, можно проверить орфографию и грамматику ремарок.

[14] В среде Mathcad 7 и 8 Pro допустимы не только числовые, но и текстовые переменные.

[15] А спрашивается, чего мучились ¾ инфляция опять ставит все на свои места. Кроме того, в 1999 году появилась новая «головная боль» ¾ евро.

[16] См. информацию в конце книги (рекламная пауза).

[17] Произведение силы на длину плеча приложения.

[18] В среде Mathcad 8 уже две системные переменные, влияющие на точность расчета: привычная TOL и новая CTOL.

[19] Гражданская война в Швейцарии в 1847 г. разгорелась на религиозно-метрической почве. Семь кантонов (Зондербунд) боролись за свои собственные меры веса и длины. Кроме того, туда подмешался давний спор католиков с протестантами. Нельзя же, в самом деле, лить кровь только из-за «футов-метров». Религиозные войны – это войны за освобождение совести человека. Наша православная церковь все еще ждет своего Цвингли, Кальвина, Лютера…

[20] Вернее, зачаток вектора ¾ переменная области (Range Variable).

[21]

По умолчанию задается не шаг, как на языке BASIC, а второе значение вектора. В нашем случае они совпадают.

[22] Читатель может сделать это вручную по технологии книжек «Раскрась сам».

[23] Это не совсем так, но уж больно удачно сравнение с ручьями и реками.

[24] Расхождение можно наблюдать в трактовке даже самых простых понятий. Так упоминавшиеся нами углы, которым соотносятся значения синуса, с точки зрения математика – это множество с бесконечным числом элементов. Для программистов же углы – это множество с сугубо конечным числом элементов. Если точность – одна десятая углового градуса (обычная точность технических расчетов), то множество углов в круге имеет всего лишь 3600 элементов. Реальное число в математике и реальное число конкретного языка программирования (тип real в языке Pascal или тип Single в языке BASIC)– это, как говорится, две большие разницы. Эта тенденция хорошо описана в книге Дж. Кемени, Дж. Снелла и Дж. Томпсона «Введение в конечную математику» (Издательство Иностранной литературы, 1963). Дж. Кемени, кстати, является одним из создателей языка BASIC.

это по своей сути имена

Сочетания арш и руб – это по своей сути имена переменных, которые в задаче на рис. 1.4 остаются пустыми и служат только для контроля размерности. Если на рис. 1.4 символ «®» заменить на «=», то Mathcad выдаст сообщение об ошибке: переменные арш и руб будут выделены красным цветом. До включения переменных в выражения им необходимо задать какое-либо числовое значение. Эту работу в среде Mathcad выполняют два оператора:
- := -                                      - º -
Первый оператор появляется на экране дисплея после нажатия соответствующей кнопки «калькулятора» (см. левый нижний угол на панели Arithmetic рис. 1.3) или после нажатия клавиши «:» клавиатуры (второй символ – «=» Mathcad любезно добавит сам). Второй оператор – «º» хранит панель Evaluation. Кроме того, символ «º» можно напечатать, нажав клавишу «~».
В левом квадрате операторов присвоения указывается имя переменной[3]
(или функции – см. раздел 1.4), а в правом – значение, которое ей присваивается. Оператор «:=» распространяет свое «влияние» вниз и вправо, а оператор «º» – на все четыре стороны. Эта особенность показана на рис. 1.5: там исходные данные максимально приближены к ответу. Если исходные данные перенести на их обычное место – в начало документа, то вместо оператора «º» можно будет использовать оператор «:=». Структура данных, показанная на рис. 1.5, удобна в объемных документах: пользователь меняет исходные данные и получает ответ без прокрутки самого документа. В «беспеременных» вариантах решения задачи о купце и сукне (рис. 1.1 и 1.4) исходные данные менять проблематично.
Еще одно отличие оператора «º» от оператора «:» – правый операнд оператора «º» может хранить системные переменные и константы (см. приложение 4), но не переменные, введенные пользователем:

Условно считается, что оператор «:=» служит для задания значений переменным, а оператор «º» – константам, то есть переменным, не меняющим свои значения в процессе решения задач.
В документе на рис. 1.4 – только текстовые поля; областей формул там нет. Формулы вставлены в концы текстовых полей (вопросов) командой Math Region меню Insert. Это очень удобно – формула и комментарий к ней составляют одно целое, которое не рвется при перемещении фрагмента документа на новое место.


Вот типичный фрагмент Mathcad-документа:


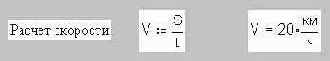
Здесь имеется три фрагмента: комментарий и два оператора – присваивание (переменные S и t определены где-то выше) и вычисление. Чтобы эти фрагменты не «разбежались» при редактировании Mathcad-документа, нужно поступить так – написать комментарий ({ – это пробел):
Расчет скорости{{{{{{
Затем в конец комментария и в середину цепочки пробелов вставить две области формул (Insert – Math Region):
Расчет скорости{{{g{{{g
После этого в черные квадратики можно будет вставить операторы присваивания и вывода результата. Получается некий единый программный блок (о нем речь впереди ¾ в этюде 6), удобный вот еще чем: если в вышеописанном фрагменте расчета скорости оператор присваивания значения переменной V несколько приподнять, то нарушится причинно-следственная связь и появится сообщение об ошибке: «Переменная (функция) не определена». Эта ошибка неприятна своей непонятностью ¾ пользователь не знает, в чем дело, и начинает ползать по всему Mathcad-документу: «Ищу рукавицы, а они за поясом».
На рис. 1.4 переменные (арш и руб) были пустыми. На рис. 1.5 все переменные (Ч, С, СЧ, Сукно, Цена_Черного, Цена_Синего, Синее и Черное[4]) хранят конкретные числовые значения. На имена переменных накладываются некоторые ограничения. В частности, в них недопустимы пробелы (их можно ставить только в комментариях), которые обычно заменяют на символ подчеркивания. Сокращение имен (Ч, С и СЧ) оттеняет вспомогательность соответствующих переменных.

и сукне из чеховского рассказа

А теперь рассмотрим второй (Петин) вариант решения задачи о купце и сукне из чеховского рассказа «Репетитор».
Петя повторяет задачу и тотчас же, ни слова не говоря, начинает делить 540 на 138.
Итак, Петя пытался поделить стоимость сукна на его «аршинаж» и вопреки протестам Зиберова был в чем-то прав: пакету Mathcad для решения системы алгебраических уравнений нужно сообщить первое, пусть даже «глупое» приближение. Все остальное он доделает сам, подчиняясь командам Given (дано) и Find (найти).

Задача о купце и сукне: решение Пети

Mathcad не назывался бы математическим пакетом, если б не умел решать системы, тем более состоящие всего лишь из двух алгебраических уравнений (любимая задача литераторов ¾ см. начало этюда). Нужно только задать начальные значения переменных. Пусть они будут равны первому («глупому») Петиному предположению: 540 разделить на 138. За ключевым словом Given (дано) пользователь должен записать анализируемую систему[5], связывая левые и правые части уравнений знаком «эквивалентно»: жирным знаком «равно» из панели Evaluation (аккорд Ctrl + =). Решить записанную систему поможет встроенная функция Find (найти). Это немного странная функция – она возвращает свое значение, зависящее не только от значений ее аргументов (здесь переменные Синее и Черное), но и от того, что около данной функции написано. Это «около» распространяется вверх (или влево) от выражения, использующего функцию Find, до ключевого слова Given и даже дальше – до начального приближения. Функция Find возвращает и заносит в переменную Ответ (это не скаляр, а вектор – матрица с одним столбцом и двумя строками) значения переменных Синее и Черное, превращающие наши два уравнения в тождества. Значения, хранящиеся в векторе Ответ, можно вывести на дисплей, поставив после имени переменной «светлый» знак равно (оператор вывода числового значения). Числа 63 и 75 охвачены скобками, подчеркивающими, что переменная Ответ – это вектор, то есть группа скалярных величин[6], объединенных в «один кулак» и подчиняющихся общей дисциплине, описываемой в особом разделе математики под названием «линейная алгебра». В среде Mathcad есть богатый набор функций и операторов работы с векторами и матрицами (см. рис. 1.3 и приложения 3 и 4), позволяющий легко и изящно решать довольно сложные задачи.
В конце рис. 1.6 представлен и второй вариант вывода результата – не распечаткой значения вектора Ответ, а распечаткой значений элементов[7]
вектора Ответ: переменных с индексом Ответ0 и Ответ1. По умолчанию в среде Mathcad первый элемент вектора имеет нулевой номер.

Термины вектор
и матрица (массив), только что промелькнувшие в нашем повествовании, подсказывают третье – Зиберовское решение задачи о купце и сукне, отображенное на рис. 1.7.
Жан-Франсуа Шампольон открыл тайну египетских иероглифов с помощью Розетского камня, где один и тот же текст был высечен по-древнеегипетски и по-древнегречески. Билингва решения задачи Удодова (пункт 1 на рис. 1.7) поможет читателям, знающим язык BASIC, понять особенности и достоинства Mathcad. Решая задачу Удодова (см. рис. 1.1, 1.4, 1.6 и 1.7), мы познакомились с четырьмя операторами, давшими пакету Mathcad второе название – суперкалькулятор, с операторами присваивания «:=» или «º» и операторами вывода результата «=» или «®». Операторы вывода нередко называют операторами распечатки переменной или выражения, напоминая тем самым о его аналоге на языке BASIC – операторе Print. Рис. 1.7 покажет нам и другие аналоги операторов и функций Mathcad в языке BASIC (феномен Розетского камня).

Задача о купце и сукне: решение Зиберова

Попытаемся, подражая Чехову, устами репетитора Зиберова растолковать ученику Пете «матричное» решение нашей задачи в среде Mathcad.
– Это задача, собственно говоря, алгебраическая, – говорит он. – Ее с иксом и игреком решить можно. Впрочем, можно и так решить (Внимание! Текст Чехова кончился). С одним иксом. Для этого перепишем задачу в матричном виде: A×X=B. Матрица A – это квадратная матрица порядка 2 (с двумя строками и двумя столбцами), хранящая коэффициенты при неизвестных системы двух линейных алгебраических уравнений, вектор X – вектор неизвестных системы, а вектор B – вектор свободных членов. Итак (см. рис. 1.7), я в среде Mathcad пишу A:. Машина приписала знак равно так, чтобы получился оператор присваивания («A:= g»), и ждет, какое значение я введу в переменную A. Ввожу я не число и не переменную, а матрицу, для чего нажимаю на кнопки с изображением матрицы на панелях инструментов Mathcad (Math и Matrix). После этого на экране дисплея возникает окно работы с матрицами Insert Matrix.
В этом окне два поля и четыре кнопки. В первом поле пользователь задает число строк (Rows) создаваемой матрицы, а во втором – число столбцов (Columns). По умолчанию в этих полях записаны тройки: считается, что квадратная матрица порядка 3 – самая распространенная. Но наша матрица А имеет порядок 2, поэтому тройки в полях окна работы с матрицами нужно заменить на двойки. На каждой из кнопок окна работы с матрицами есть надписи: OK (Создать матрицу и закрыть окно), Insert (Вставить), Delete (Удалить) и Canc el (отмена). Матрицу мы создаем, поэтому щелкаем по кнопке OK. Две остальные кнопки предназначены для изменения размеров ранее созданных матриц: заданное в полях число столбцов и/или строк вставляется (удаляется) правее и ниже отмеченного курсором элемента уже созданной матрицы.
После щелчка по кнопке OK справа от выражения А:= появляется каре четырех вакантных мест для ввода информации, обрамленное скобками. Заполняем вакансии числами 1, 1, 5 и 3 и приступаем к формированию вектора В. Набираем В:= и снова вызываем окно работы с матрицами[8]. Во втором поле меняем двойку на единицу, щелкаем по кнопке OK и получаем заготовку для ввода информации в вектор В. Заполняем вакантные места числами 138 («аршинаж» сукна) и 540 (его стоимость). Все! Матрица и вектор коэффициентов системы линейных алгебраических уравнений заполнены, значит основная работа сделана. Остается только найти решение системы и заполнить им матрицу X. Для этого инвертированную (обратную, возведенную в минус первую степень) матрицу A перемножаем на вектор B, а ответ заносим в вектор X. Если мы теперь введем с клавиатуры Х=, то машина выдаст нам ответ – числа 63 и 75 в скобках, что еще раз подчеркивает их матричный характер. (Внимание! Подражание Чехову закончилось).

Через окно Insert Matrix можно ввести матрицу, у которой число элементов не может превышать ста. Считается, что большее число элементов матрицы неразумно вводить вручную. Объемные матрицы вводятся в Mathcad-документ тремя способами:
1. Элементы матрицы хранятся файлом на диске и вводятся в матрицу функцией READPRN.
2. Две матрицы сливаются в одну функциями stack (матрицы ставятся одна на одну) или augment (матрицы ставятся бок о бок).
3.

Двумя циклами формируется объемная вспомогательная матрица (M1), хранящая единицу или что-то другое, а потом ее содержимое копируется в создаваемую матрицу M и редактируется:
На рис. 1.7 правее Mathcad-выражений помещены комментарии, показывающие, как задача о купце и сукне решается с помощью языка BASIC, имеющего «матричные» операторы, начинающиеся с ключевого слова Mat. В языках программирования векторам и матрицам соответствуют массивы, хранящие переменные с индексом, которые подсказывают нам второй вариант «матричного» решения задачи о купце и сукне (пункт 2 на рис 1.7) без обращения к окну работы с матрицами, а через ввод индекса переменной: Аi , j, Bi и Хi. Индекс к имени переменной добавляется либо нажатием на кнопку Хn панели Matrix, либо на клавишу «[» (открывающаяся квадратная скобка). Запомнить эту клавишу просто: на языках Pascal и C в квадратные скобки помещаются индексы переменных A[i, j], B[i], Х[i] и т.д. Можно отметить еще одну особенность второго варианта «матричного» решения задачи Удодова: отказ от умножения инвертированной матрицы А на вектор В, а использование вместо этого встроенной функции lsolve, возвращающей решение (to solve – решать) системы линейных (l – эль) алгебраических уравнений.
В среде Mathcad 8 появились дополнительные возможности решения систем алгебраических уравнений конструкцией Given-Find, проиллюстрированные на рис. 1.8. Система уравнений, решаемая на рис. 1.8, имеет два корня, которые хорошо видны на графике (см. пункт 1, как он строится ¾ см. ниже главку «Великолепная семерка Mathcad»). Функция Find возвращает одно решение вблизи точки начального приближения. Но если начальное приближение дать не в виде скаляра, как на рис. 1.6, а в виде вектора (см. пункт 2 на рис. 1.8), то ответ будет содержать все корни системы. Элементы вектора Ответ ¾ уже не скалярные величины, а новые векторы.
Кроме того, в среде Mathcad 8 появилась возможность переменные системы алгебраических уравнений объединить в вектор. Этот прием проиллюстрирован в пункте 3 на рис. 1.8. В среде Mathcad 8 нет необходимости делать число уравнений большим или равным числу неизвестных системы.
Еще одно новшество Mathcad 8: если поместить курсор мыши на функцию Find и нажать правую кнопку мыши, то выпадает так называемое контекстное меню, в котором реализована возможность выбора метода решения системы алгебраических уравнений (см. конец рис. 1.8). Система Mathcad 8 по умолчанию сама выбирает метод решения (AutoSelect). Но пользователь при необходимости может скорректировать метод и детали расчета. В среде Mathcad 8 Pro можно решить систему, состоящую из 200 нелинейных алгебраических уравнений[9].

к решению одного алгебраического уравнения,

Задачу о купце и сукне можно свести к решению одного алгебраического уравнения, получаемого подстановкой:

Черное = 138 – Синее

5 × Синее + 3 × (138 – Синее) = 540

Для поиска корня уравнения с одним неизвестным можно также использовать конструкцию Given-Find, принимая во внимание тот факт, что одиночное алгебраическое уравнение – это не что иное, как система из одного алгебраического уравнения.

На рис. 1.9. дано решение в среде Mathcad старинной русской загадки: «Летят гуси, а с земли их спрашивают: «Гуси, гуси, сколько вас?». Следует ответ: «Если нас будет столько, а потом полстолько, и еще четверть столько да еще два гуся, то нас будет ровно сто». Ответ – 56 гусей:

Задача о гусях

Но для решения одиночных алгебраических уравнений лучше использовать не конструкцию Given-Find, а встроенную функцию root (а root, по-английски, корень).

Задача о пожарном ведре: схема решения

Требуется найти угол вырезки a (альфа), при котором объем ведра будет максимальным.
Эту оптимизационную задачу можно решить аналитически: см. пункт 3.3 на рис. 2.1. Но, как понимает читатель, далеко не всякую математическую задачу можно решить аналитически. Иначе бы не было таких научных дисциплин, как «Прикладная математика», «Программирование», «Численные методы» и др. Поэтому мы рассмотрим численное
решение задачи.
И при численном, и при аналитическом решении задачи мы должны вывести зависимость объема ведра V от угла вырезки a. Далее при аналитическом решении можно взять первую производную от этой функции, приравнять ее к нулю и найти корень полученного уравнения. Не обойтись тут и без второй производной, если нужно убедиться, что найденное решение – максимум, а не минимум или точка перегиба, где, как помнит читатель из курса матанализа, первая производная также равна нулю. Жестянщик, которому поручат сделать пожарное ведро, скорее всего, незнаком с дифференциальным счислением, азы которого мы только что изложили. Но в среде Mathcad поставленная задача вполне окажется по плечу «компьютеризированному» жестянщику.
Рисунок заготовки ведра и самого ведра в пункте 1 на рис. 2.1
сделан с помощью графического редактора Paintbrush и перенесен в Mathcad-документ через буфер обмена Clipboard.
В пункт 2 на рис. 2.1 скопированы данные о геометрии конуса из стандартного справочника Mathcad, который удобен тем, что входит в состав пакета и всегда находится под рукой. Справочник открывается командой Open Book… в меню Help. Перенос данных из справочника в Mathcad-документ также автоматизирован, что исключает их искажение – списывая формулу из книги немудрено и ошибиться.
Пункт 3 на рис. 2.1 – это «воспоминание о будущем». Там записаны операторы символьных (аналитических) преобразований (см. этюд 7). В пункте 3.1 оператором solve решается алгебраическое уравнение, позволяющее сформулировать функции пользователя с именами r, h и V (см. пункт 3.2). Зависимости выводятся из несложной геометрии круга и конуса: длина дуги выкройки (2×p×R-2×p×R×a/360) становится длиной окружности в основании конуса (2×p×r), а высота конуса h, радиус его основания r и радиус заготовки R ¾ это стороны прямоугольного треугольника, длины которых связаны теоремой Пифагора (см. пункт 3.2 на рис. 2.1). Оператор substitude позволяет заменять в выражениях подвыражение на другое и вывести еще одну формулу V(a) без вызова вспомогательных функций r(a) и h(a) – см. конец пункта 3.2 на рис. 2.1.
В пункте 3.3 берется производная от V(a), которая сразу упрощается (оператором символьного преобразования simplify). Несложный анализ вида производной показывает, что оптимальный угол вырезки – это один из корней квадратного уравнения a2-720a+43200. Но мы пока на это не обращаем внимания и начинаем численное решение задачи.

Транспортная задача

Спрашивается, как нужно организовать перевозки (найти значения переменных с1м1, с1м2, с2м1 и с2м2), чтобы затраты были минимальны. На рис. 2.10 дан ответ. Парадокс задачи в том, что по самому дешевому маршруту (со второго склада в первый магазин – 800 у.е.) ничего не возится (с2м1 = 0). Этот парадокс мы также обыграем в следующем этюде.
Задачи на рис. 2.9 и.2.10 простенькие, но очень, если так можно выразиться, жизненно важные. На каждом шагу приходится что-то оптимизировать (расходы, например), принимая во внимание всякого рода ограничения (доходы!). Возвращаясь к сноске 17, можно привести такой пример. После часа пик (зимнее утро, к примеру) расход электроэнергии падает и необходимо снижать нагрузку электрогенераторов. Как это делать? Можно отключить отдельные турбогенераторы, а можно оставить их в работе, изменив нагрузку. Диспетчер энергосистемы дает соответствующие команды, ориентируясь на некие целевые функции: средний расход топлива по системе, выброс с дымовыми газами вредных веществ в атмосферу, износ оборудования, степень готовности электростанций и дальше менять нагрузку и т.д. Переменные такой оптимизации могут быть и вещественными (мощность отдельного энергоблока, которая меняется, естественно, в разумных пределах, определяемых техническими условиями – ограничения в задаче) и целочисленными (число работающих блоков). Эта задача очень сложная, но и очень эффективная – здесь речь идет о высвобождаемых составах с топливом.
Вот еще примеры. Когда нужно убирать пшеницу? Пораньше – зерно еще не вызрело. Попозже – часть зерна уже осыпалась. Сколько и каких акций стоит купить на ограниченную сумму денег, чтобы будущий дивиденд был максимален? В каких средствах массовой информации стоит размещать рекламу на выделенные по смете деньги, чтобы эффект от нее был максимален?
Разговор об оптимизации мы продолжим в этюде 3 в несколько ином ключе.
[1] Тем более что, переменная R уже занята под хранение градусов Ренкина. В этом можно убедиться, набрав R= и получив R=0.556 K (градус Ренкина в градусах Кельвина). Присвоением R:=1m мы «испортили» данную системную переменную, что может выйти нам боком, если в расчет придется вводить температуру. Отсюда вытекает хорошее правило работы в среде Mathcad: «Никогда не пользуйтесь оператором «:=». Для присваивания значения переменной лучше работать с оператором «=», автоматически превращающимся в оператор «:=», если соответствующая переменная не занята пользователем или системой.

[2] В предыдущем издании книги автор так и написал R:=1 без указания, что это не просто единица, а единица длины. Из-за этого в формуле для h была допущена, а, главное, не исправлена, ошибка, сказавшаяся бы на расчете, если бы R стала равна не единице, а, допустим, двум.

[3] Такую работу может сделать и «Лупа» графика – см. рис. 1.26.

[4] Здесь ? не символ суммы, а просто заглавная греческая буква «сигма». Три функции вводятся в график через запятую, но автоматически выстраиваются столбиком.

[5] Автор, служа в армии и моя там, как водится, полы, ставил пожарное ведро (другого не было) в перевернутую табуретку. Отсюда и «любовь» к пожарным ведрам, вылившаяся на страницы этой книги.

[6] Эту функцию мы еще помянем добрым словом ¾ см. сноску 13.

[7] В среде Mathcad допустимо разрывать длинные суммы для более компактного их размещения на экране дисплея и на бумаге принтера. Для этого нужно нажать Ctrl+Enter вместо плюса.

[8] У нас получились некие лестницы, которые мы еще обыграем, рассказывая о чувствах, которые могут охватывать пользователя Mathcad.

[9] Эта возможность появилась еще в седьмой версии Mathcad.

[10] В среде Mathcad 8 эту работу можно делать по новой технологии: прижать график левой кнопкой мыши и вращать его, двигая мышь.

[11] Функция max здесь работает в качестве логического ИЛИ – см. в этюде 3 главку «Mathcad и булевы (логические) функции»: если a<0, или b<0, или a+b>360, то объем ведра становится равным нулю, иначе – сумме объемов трех ведер.

[12] Здесь звездочка это 4, 5 и 6. Пользователям ЭВМ такое сокращение (обобщение) знакомо по работе с файлами.

[13] Библейские герои за свои заслуги перед Богом получали дополнительную гласную в свое имя: Был Аврам (Абрам), стал Авраам (Исак – Исаак и т.д.). В Mathcad 8 имя нашей «заслуженной» функции изменилось: было minerr (или Minerr), стало MinErr.

[14] Треугольник – это основа визуализации трехкомпонентных смесей

(сплавов): поверхность над таким треугольником отображает какой-либо параметр (плотность сплава, к примеру), а стороны треугольника – это процентное содержание каждого из трех компонентов. Углы треугольника – чистый металл, стороны – двухкомпонентный сплав, а нутро треугольника – трехкомпонентный сплав. Очень часто здесь, как в драке, третий оказывается лишним. Так, например, припой для пайки – это сплав свинца с оловом, имеющий минимальную (опять оптимизация) температуру плавления. Добавление в припой третьего металла (цинка, например) только ухудшает этот основной его технологический показатель.

[15] Это, естественно, не доллары США, а на самом деле условные единицы, не влияющие на решение задачи.

[16] Автор сначала хотел было написать «компьютеров», ориентируясь на тематику данной книги, но потом передумал – см. следующую сноску.

[17] Автор на своих лекциях в Московском энергетическом институте заменяет магазины на электростанции, куда из шахт

подвозится уголь. Одним словом, «Служил Гаврила почтальоном, Гаврила уголь, пардон, почту развозил…» – см. предыдущую сноску. Уголь удобен тем, что это не целочисленная задача.

Решение задачи о пожарном ведре

Пусть радиус заготовки R равен одному метру (см. начало рис. 2.2). Это можно было бы и не оговаривать[1], так как значение оптимального угла вырезки не зависит от радиуса заготовки (см. конец рис. 2.1), но для численного
решения задачи о пожарном ведре это необходимо. Правда, можно было написать проще – R:=1, не привязываясь к метрам (литрам, галлонам – см. ниже). Но единицы физических величин позволяют нам дополнительно вести контроль правильности формул через соответствие размерностей[2].
Далее записана (вернее, скопирована из рис. 2.1) цепочка функций пользователя, формирующая нашу анализируемую функцию V(a), в которую вложены другие функции – r(a) и h(a). В последнюю в свою очередь также вложена функция r(a). Механизм вложения функций и операторов (встроенных и пользовательских) ¾ это мощный инструмент не только Mathcad, но и других программных сред, позволяющий быстро и изящно решать довольно сложные задач. Вложенные функции просты по виду, а механизм их формирования открыт, чего не скажешь о функции V(a) в пункте 3.2 на рис. 2.1.
Прежде чем искать максимум функции, необходимо убедиться, что он есть. Лучший же способ увидеть максимум – просмотреть график функции. В среде Mathcad есть семь видов графиков (см. этюд 1), первый из которых (X-Y-график в декартовых координатах) отображен на рис. 2.2. Здесь график построен по «двухшаговой» технологии: задается вид функции и сразу отдается команда на вставку графика в Mathcad-документ. По умолчанию аргумент меняется от минус 10 до плюс 10 с пятьюдесятью точками на графике. После построения наброска графика его нужно будет отформатировать – изменить разброс аргумента и др.
На графике в районе 60-70 градусов отчетливо виден максимум функции. Как его уточнить?
Для решения такой задачи в Mathcad 8 встроена новая функция Maximize, возвращающая координаты максимума анализируемой функции вблизи точки начального приближения. Если из заготовки вырезать сектор с углом в 66 с чем-то градусов, то такое ведро будет иметь максимальную вместимость ¾ 403 литра (106 с половиной американских или 88 с половиной британских галлонов – продолжение темы единиц измерения физических величин, начатой в этюде 1).

Заканчивается численное решение задачи о пожарном ведре проверкой правильности решения: Доверяй, но проверяй! Для этого, во-первых, оно сравнивается с аналитическим (абсолютно точным, скопированным из рис. 2.1). Во-вторых, построен график той же функции, но на ином интервале значений аргумента – вблизи найденной точки максимума: в интервале 65-67 градусов с шагом 0.1[3]. Уточняющий график построен уже по «трехшаговой» технологии ¾ с заданием области значений переменной-аргумента a. На это приходится идти, так как переменная a к этому моменту уже имеет скалярное значение, которое мешает строить график в два шага.
На рис. 2.2 читатель может видеть переменную с индексом a опт. Но здесь индекс опт (оптимальное) не числовой, как на рис. 1.6 и 1.7, а текстовый. Числовой индекс должен иметь определенное целочисленное значение, отмечающее место переменной в векторе или в матрице. Текстовый же индекс – это всего лишь продолжение имени переменной (функции). Он вводится в Mathcad-документ для эстетического эффекта – чтобы переменные были более наглядными. Получается текстовый индекс после того, как в середину имени переменной поставят точку: было a.опт, стало a опт. Числовой же индекс, как помнит читатель, вводится либо через квадратную скобку (X[n – Xn), либо через специальную кнопку Xn панели инструментов Matrix.
Попробуем усложнить задачу о пожарном ведре. Что если вырезанный из заготовки сектор не выбрасывать, а скручивать из него второе коническое ведро? Вместимость двух ведер, естественно, будет больше вместимости одного ведра. Вопрос на пари: как необходимо раскроить заготовку, чтобы суммарный объем двух ведер был максимальным? Большинство опрошенных, опираясь на здравый смысл, ответят, что заготовку нужно разрезать пополам по диаметру, и... проиграют пари.

Решение задачи о двух пожарных ведрах

На рис. 2.3 показано численное решение «двухведерной задачи» в среде Mathcad. В основном оно повторяет решение, показанное на рис. 2.2, но имеет такие особенности:

Сделано допущение, что радиус заготовки равен единице – переменная R в расчете отсутствует.

Функция объема ведра не опирается на вложенные функции. Это несколько усложняет понимание сути задачи, но ускоряет расчет.

Объем второго ведра рассчитывается также через функцию V, но аргумент a при этом сдвинут на 360 градусов: второму ведру достаются обрезки от первого ведра.

На первом графике выведена не одна кривая, а три: объем первого ведра V(a), объем второго ведра V(360 - a) и сумма объемов обоих ведер SV(a)[4]. Кроме того, шкала оси функции начата не с нуля, а со значения 0.38 для того, чтобы пользователь отчетливо увидел два максимума у функции SV и выиграл пари: заготовку нужно разрезать не по диаметру, а несколько иначе, чтобы получить два разных ведра, но с максимальным суммарным объемом.

Построен график производной функции SV, на котором видны три точки пересечения кривой с осью абсцисс, свидетельствующих о двух симметричных максимумах и об одном локальном минимуме в середине. При форматировании первый график был обрамлен (умолчание), а на втором прорисованы оси X и Y. Второй график строится намного дольше первого из-за того, что значение производной в каждой точке графика приходится высчитывать, используя алгоритм численного дифференцирования. А это сама по себе довольно сложная задача. Можно, конечно, из рис. 2.1 скопировать в рис. 2.2 выражение для производной и работать уже с ней, но мы договорились решить задачу только численными методами.

Максимумы для разнообразия найдены не через функцию Maximize, как на рис. 2.2, а через поиск корней производной функции SV. Для этого в расчет включена встроенная функция root, возвращающая корень уравнения и тоже требующая первого приближения к решению. Изменили первое приближение с 120 на 240 угловых градусов ¾ и ответ иной (второй). Кроме того, пришлось изменить c 10-3 на 10-6

значение системной переменной TOL, отвечающей за точность нахождения корня: наша производная вблизи максимумов и минимума меняется очень слабо – в пределах 10-4.
Пожарное ведро делается в виде конуса для того, чтобы его нельзя было поставить на пол, а потом использовать не по прямому назначению (для стирки, например) – такое ведро свалится на бок[5]. Решение задачи о двух пожарных ведрах также «валится на бок» – на «левый» (a < 180) или на «правый» (a >180). Такую же форму (конус без ножки) имеет бокал типа «Пей до дна!».
Не выбросив меньший сектор и сделав из него второе пожарное ведро, мы мало что выиграли – второе ведро дало небольшую прибавку в объеме (~ 50 литров). Раскрой заготовки для двух ведер не по диаметру (a=180), а хитрым способом дал совсем ничтожный выигрыш по суммарному объему ведер (что-то около литра). Но нам важен не результат, а сам процесс расчета: «Цель ничто, движение – все!»
Теперь решим задачу, подобную задаче о пожарном ведре, но более простую и более известную – задачу о максимальном объеме коробки (см. рис. 2.4). Она тоже будет иметь интересное продолжение, связанное с утилизацией отходов.

Решение задачи о коробке

У квадратной жестянки по углам вырезаются четыре квадрата. Полученная таким образом крестообразная заготовка сгибается по пунктиру в прямоугольную призму без верхней крышки, а четыре шва свариваются (паяются). Требуется рассчитать размер сторон вырезаемых квадратов (a ¾ отношение размеров квадратов), при котором объем нашего «квадратного ведра» (коробки) будет максимальным.
На рис. 2.4 показано численное решение задачи. Оно отличается от решения по пожарному ведру (см. рис. 2.2) только видом анализируемой функции и методом оптимизации: использована функция MinErr[6] в паре с ключевым словом Given, между которыми булево равенство и ограничение, заставляющее систему искать локальный, а не глобальный максимум.
Несложный анализ функции V(a) показывает, что она имеет максимум при a=1/6. Это позволяет оценить точность использованного нами метода численной оптимизации.
Продолжение задачи о коробке также похоже на продолжение задачи о пожарном ведре: обрезки идут на изготовление новых четырех коробок, новые обрезки (их уже будет 16) тоже пойдут в дело, и так до бесконечности. Но до нее (до бесконечности) мы доберемся только в этюде 7, сейчас же рассмотрим только первые семь шагов раскроя квадратной заготовки, приводящих к формированию 5461 (1+4+16+43+44+45+46) коробок-«матрешек» (рис. 2.5).

определяющую объем плодящихся вышеописанным способом

Формулу, определяющую объем плодящихся вышеописанным способом коробок, вывести несложно[7]. Если допустить, что величина a (отношение размера вырезки к размеру заготовки) сохраняется по шагам раскроя, легко показать, что сторона исходного квадрата равна a0, четырех новых – a1, шестнадцати последующих – a2 и т.д.
Теперь спрашивается (еще одно пари!), как нужно кроить заготовки: чему должно быть равно значение a, чтобы суммарный объем коробок был максимальным?
Ответ, лежащий на поверхности, – пропорция выкройки a должна быть такой, какой она была для одной коробки (одна шестая – см. рис. 2.4). Если одна коробка имеет максимальный объем, то его будут иметь и несколько коробок! Но это не так – оптимальная точка смещается вправо по оси аргументов по мере выполнения все новых и новых шагов раскроя. На рис. 2.5 для сравнения выведены две кривые: зависимость от значения a объема одной коробки и объема 5461 коробки. Прирост объема ничтожный, но нам опять же важен не результат, а процесс расчета. Особенно наглядно это видно на рис. 2.6, где приведена формула расчета суммарного объема коробок в зависимости от пропорции выкройки a и от числа шагов раскроя n.

величина a) является функцией числа

В задаче на рис. 2.6 оптимальный размер раскроя ( величина a) является функцией числа шагов, что позволяет протабулировать аргумент и функцию и проследить дрейф оптимума и прирост суммарного объема ведер. Как видно из таблиц[8], где-то в районе 7-8 шагов раскроя точность Mathcad становится недостаточной: ответы по переменной a начинают изменяться непредсказуемо, а по V – совсем не изменяются.
При поиске оптимального раскроя коробок (рис. 2.5 и 2.6) мы предположили, что величина a, при которой суммарный объем коробок максимален, должна быть одной и той же и для больших, и для маленьких коробок. Тем самым мы свели задачу к оптимизации функции одной переменной (одномерная
оптимизация). На рис. 2.7 это ограничение снято.

суммарный объем коробок рассчитывается

На рис. 2. 7 суммарный объем коробок рассчитывается как функция уже не одного, а нескольких аргументов: первый шаг раскроя – один аргумент (пункт 1), второй шаг – два аргумента (пункт 2), третий шаг – три аргумента и т.д. В пункте 1 рис. 2.7 для сравнения использованы три допустимых в Mathcad способа поиска максимума и рассчитаны отклонения от аналитического решения при проектировании одной коробки. В пункте 2 рис. 2.7 найдены оптимальные значения переменных a и b (пропорции выкройки большого квадрата и четырех маленьких квадратиков соответственно), при которых объем пяти коробок будет максимальным (двухмерная оптимизация). Мы забыли наложить ограничения на переменные a и b в блоке Given-MinErr и второй результат оказался неверным. В пункте 3 найденный оптимум проверяется на двух графиках – на линиях уровня и на поверхности.
В среде Mathcad 8 операторы, которые разработчик документа по каким-то причинам не хочет показывать другим людям, можно оконтурить сверху и снизу границами области (команда Area в меню Insert), которую затем можно захлопнуть (команда Area-Collapse в меню Format). Это нами и сделано в пункте 3 на рис. 2.7 – там запрятаны (см. след в виде горизонтальной линии) рутинные операторы формирования матрицы M, по элементам которой строятся трехмерные графики. Если теперь по этой линии два раза щелкнуть левой кнопкой мыши (или щелкнуть раз и отдать команду Area-Expand в меню Format), то область распахнется и покажет свое содержимое:

В предыдущих версиях Mathcad операторы прятали от посторонних взглядов, помещая их за правую кромку экрана дисплея, полагая, что никто не догадается туда заглянуть (тайна Полишинеля – мы уже упоминали об этом в этюде 1).
Выделенную область можно защитить[9]
(с паролем или без оного) от редактирования (команда Area-Lock в меню Format).

Прием очень удобный. Во-первых, операторы можно прятать от самого себя – отладил какой-то участок Mathcad-документа и запрятал его от греха подальше. Другой случай. Разработчик сдал заказчику расчет, оставив на виду только зону ввода исходных данных и зону с результатом (если вернуться к рис. 1.5 с задачей о купце и сукне, то это самые нижние операторы). Остальное (что заказчику знать не следует – сам расчет) скрыто и защищено паролем. Может быть, там всего лишь пара операторов, но не простых, а гениальных. Рассказывают, что один американец починил за 1000 долларов дорогую паровую машину, стукнув по ней разок молотком. Когда ему сказали, что такая работа стоит от силы доллар, то он не стал спорить: «Да, но знание места, куда нужно бить молотком, стоит 999 долларов!»


Заканчивается рис. 2. 7 формулой, по которой можно рассчитать суммарный объем любого числа коробок, изготовленных по методике, показанной на рис. 2.5. Найдены параметры раскроя при семи шагах. У нас получилась схема оптимизации по переменному
числу аргументов. Стоит только изменить длину вектора a, тут же изменится число шагов раскроя квадратной заготовки.
Продолжение и конец решения задачи о коробках – в этюде 7, где к численным методам расчета добавятся аналитические (символьные) методы и... интеллект пользователя.
Попробуем еще немного «погреметь пожарными ведрами» и зададимся новым вопросом. Что если круглую заготовку посекторно раскроить для изготовления не одного (см. рис. 2.2) и не двух (см. рис. 2.3), а трех ведер? Сможем ли мы еще что-то «выжать» из задачи? Можно ли так раскроить круглую заготовку на три сектора и свернуть из них три конуса, чтобы превысить «двухведерный» рекорд, зафиксированный на рис. 2.3? Новая, «трехведерная» задача сводится к поиску максимума функции двух переменных: a (угол заготовки для первого ведра) и b (для второго). Третьему ведру перепадут остатки: 360-a-b.

Решение задачи о трех пожарных ведрах (начало) (середина) (конец)

На рис. 2.8 помещен протокол решения «трехведерной» задачи. Поиск максимума начат опять же с формирования функции пользователя и с ее графического анализа. Поверхность функции двух переменных строилась так, как показано в пункте 3 на рис. 2.8. Создается сетка с 1681 узлом: 41 линия (0 до 40) по оси переменной a и столько же по оси переменной b. Эта сетка кладется на плоскость a-b, а затем ее узлы (от 0 до 360 градусов с шагом 9 градусов) поднимаются по оси функции V на «подобающую» каждому узлу высоту. Далее эта ажурная конструкция с помощью диалогового окна форматирования поворачивается[10]
вокруг осей V, a и b так, чтобы человек смог увидеть то, что ему нужно, – максимумы, минимумы и др. Всю эту работу машина берет на себя. От человека требуется только наметить узлы сетки (i := 0.. 40, j := 0.. 40), дать «угловое» значение ее узлам (ai := 9×i, bj
:= 9×j – углы меняются от 0 до 360 с шагом 9), заполнить матрицу M значениями «трехведерной» функции ¾ Mi,j:= V(ai, bj), перевести курсор на свободное место и отдать команду построения трехмерного графика, отображающего элементы матрицы М.
Основной недостаток трехмерной графики Mathcad заключается в том, что область изменения аргументов должна быть прямоугольной. Но в нашей «трехведерной» задаче она треугольная, так как аргументы связаны ограничением a+b£360. В пункте 2 рис. 2.8 функция V строится так, чтобы ее значения, выходящие за рамки треугольника, приравнивались к нулю (метод штрафных санкций[11]). Из-за этого задняя грань поверхности на рис. 2.8 получилась зубчатой. Тем не менее видны максимумы на сторонах треугольника области существования аргументов a и b и провисание в центре. В трех вертикальных сечениях просматривается «двухведерный» верхний график из рис. 2.3. Пакет Mathcad не смог решить двухмерную «трехведерную» оптимизационную задачу по методике, представленной на рис. 2.3 (взятие частных производных по переменным a и b и поиск корней полученной системы алгебраических уравнений). Пакет Mathcad пытался искать максимум «у края обрыва» и «сваливался» в него. Не справилась с этой задачей и специально введенная в Mathcad 8 функция Maximize при всех трех начальных приближениях (см. пункты *.1[12]): мы «танцевали» к максимуму от трех «печек» ¾ из центра треугольника (120 и 120 градусов ¾ см. пункт 4), из одного угла треугольника (0 и 0 градусов ¾ см. пункт 5) и от одной из сторон треугольника (150 и 210 градусов ¾ см. пункт 6). С поиском максимума справилась «старая добрая» функция MinErr[13] ¾ см. пункты *.2. Старая в буквальном смысле ¾ она ведет свою родословную еще с DOS-версий Mathcad и поэтому хорошо отлажена.

В пункте 7 сделан дополнительный графический анализ через линии уровня нашей «трехведерной» задачи, которая на поверку оказалась «двухведерной». Сразу виден еще один недостаток трехмерной графики Mathcad: область существования решений ¾ это равнобедренный, а не прямоугольный треугольник[14], как в пункте 7 на рис. 2.8. Оси a и b нужно размещать не под прямым углом, а под углом в 60 градусов, но Mathcad этого делать не может.
В пункте 8 сделана попытка реабилитации функции Maximize, потерпевшей полное фиаско в пункте 6. Если функция MinErr всегда должна работать в паре с ключевым словом Given, то функция Maximize ¾ может. За ключевым словом Given при необходимости пишутся ограничения, открывающие новые возможности в решении оптимизационных задач. Если из пользовательской функции убрать штрафные санкции (переопределить ее ¾ см. начало пункта 7), то функция Maximize справится с поставленной задачей (пункты 8 и 10), если… не застрянет в «седле» (пункт 9). Мы еще раз подтвердили, что третье ведро лишнее: максимумы лежат на краю обрывов – на линиях области существования «двухведерной» задачи. Максимумов шесть. К ним можно прийти, изменяя начальные приближения.
В книге мы еще не раз будем «греметь пожарными ведрами»: в этюде 6 (тестирование программы поиска оптимума функции многих переменных) и в этюде 7 (аналитическое решение задачи о ведре).
Возможность записи перед функциями Maximize и Minimize системы ограничений в виде неравенств и равенств позволяет решать в среде Mathcad новый класс оптимизационных задач. Вот две из них.

Задача о стульях

Данная задача относится к широкому классу задач под названием задачи линейного программирования: необходимо установить план (программу!) выпуска изделий (у нас это стулья), ориентируясь на целевую функцию (у нас их две ¾ общее количество и общая стоимость стульев) и принимая во внимание ограничения
(ресурсы по доскам, ткани и человеко-часам). Из рис. 2.9 видно, что можно выпускать не более 150 стульев (максимум первой целевой функции). А вот с максимизацией их общей цены не получилось: Mathcad не умеет решать задачу целочисленного линейного программирования. План выпуска стульев, максимизирующий их количество, вышел целочисленным случайно.

Поиск корня уравнения

Теперь мы подшутим
над функцией root, и если не получим от этого удовольствия, то хотя бы уясним себе, какие «подводные камни» могут нас ожидать.
Если в качестве первого приближения (опорной точки) принять не минус 50, а плюс 5 (пункт 5), то функция root выкинет «белый флаг»: сообщение «Can’t converge to a solution», отказываясь решать поставленную задачу, хотя плюс 5 намного ближе к корню, чем минус 50. Вот вам и первое приближение! Но это еще полбеды. Настоящая беда случается тогда, когда функция root (как, впрочем, и некоторые другие функции и операторы Mathcad) не отказывается решать поставленную задачу, выдавая при этом неверный результат (феномен медвежьей услуги).
Если функцию y(x) умножить на константу, например на 10-5, то ее корни останутся на старых местах. Но это утверждение в среде Mathcad не является истиной – см. пункт 6 рис. 3.1.
Не то беда, Авдей Флюгарин,
Что родом ты не русский барин,
Что на Парнасе ты цыган...
Беда, что скучен твой роман.
Не то беда, что ты, Mathcad, неправильно решил простейшую задачу: и более мощные специализированные пакеты, ориентированные только на решение алгебраических уравнений и систем, делают тут промах. Беда в том, что Mathcad в этом честно не признался, как это было в пункте 5 на рис. 3.1.
Философский смысл любой шутки заключается в том, что у шутника и у того, над кем подшучивают, разные понятия о природе вещей. У пользователя и у среды Mathcad разные понятия о том, что такое корень уравнения: человек считает, что корень – это то значение аргумента, при котором выражение равно нулю; функция же root «считает», что корень – это то значение аргумента, при котором значение выражения по модулю не превышает значения системной переменной TOL, которая по умолчанию равна 10-3. Отсюда и путаница в пункте 6 на рис. 3.1. Чтобы функция root там сработала правильно, необходимо переменной TOL присвоить новое значение (10-7, например), заменив им предопределенное. Можно поступить и по-другому – умножить в пункте 6 правую часть функции на 100000, убрав тем самым коэффициент 0.00001. Метод балластных (нормирующих) коэффициентов особенно эффективен при решении алгебраических систем (что уже было отмечено в этюде 1). Он позволяет уравнять все уравнения (прошу простить за тавтологию) по отношению к точности, с которой система решается через блок Given-Find. На нижнем графике рисунка 3.1 ось X «утолщена» до значения TOL (пунктир). Корень там, где кривая касается этой «толстой» оси.

В среде Mathcad 8 переменная TOL была дополнена еще одной системной переменной ¾ CTOL (tolerance of the constraints ¾ точность ограничений), которая также по умолчанию равна 10-3, но уже отвечает не за поиск корней и оптимумов, а за ограничения ¾ за уравнения и неравенства, записанные после ключевого слова Given.

С промахом, зафиксированным в пункте 5 рис. 3.1, можно разобраться после знакомства с вычислительными методами, заложенными в функцию root. В Руководстве пользователя Mathcad сказано, что функция root ищет корень выражения методом секущих, и дано его описание, которое автор перевел на язык BASIC.

' Поиск корня уравнения методом секущих

' Реализация на языке BASIC Mathcad-функции root



Def FnY(x) = 2 * X ^ 3 + 20 * x ^ 2 – 2 * x + 100 ' Анализируемая функция

TOL = 0.001 ‘ Точность поиска корня

‘ Начало процедуры поиска корня

Input "X нач. :=", X ‘ Начальное приближение

If Abs(FnY(X)) < TOL Then

            root = X ‘ Начальное приближение и есть корень уравнения

  Else ‘ Расчет второй опорной точки

            If X = 0 Then h = TOL Else h = X * TOL

            X0 = X : X1 = X + h

            Do ‘ Цикл приближения к корню

                        root = X1 – FnY(X1) * (X1 – X0) / (FnY(X1) – FnY(X0))

                        X0 = X1: X1 = root ' Подготовка к следующему приближению

            Loop Until Abs(FnY(X1)) <= TOL ‘ Условие завершения цикла

End If

Print

"Y=0 при X="; root ‘ Вывод результата

Определение плана выпуска стульев: перебор

Оказывается, при переборе всех вариантов выпуска стульев (а их не так уж много – на рис. 3.10 мы просчитали 150 на 150 = 22 500 вариантов) можно найти два оптимальных плана, причем самый оптимальный и по цене, и по количеству (20+112=132 стула стоимостью 1504 у.е.) – это не округление дробного ответа, полученного на рис. 2.9. Возвращаясь к теме враждебности задачи, можно так подобрать ее условия, что ответ окажется совсем вдалеке от первоначального дробного…
Это был эпиграф, приступаем к рассказу.
У Михаила Жванецкого часто спрашивают, откуда он берет темы для своих миниатюр. «Выглядываю в окно и прислушиваюсь к разговорам на улице», – таков ответ великого сатирика. «А как Вы все это запоминаете?», – следует новый вопрос. «Да я забыть не могу!»
Житейские сюжеты стоит коллекционировать и для написания компьютерных этюдов, что является хобби автора этой книги.
По профессии автор – преподаватель вуза (Московского энергетического института), где он читает курс лекций по информатике и смежным дисциплинам, а также руководит группой технологов и программистов, разрабатывающих обучающие программы и компьютерные тренажеры для ТЭС и АЭС[12]. Электростанциям и энергообъединениям нужны наши программы, но их приобретению мешает пресловутый кризис неплатежей. Вот какой компьютерный этюд имел место в марте 1997 года.
Акционерное общество Тамбовэнерго, не имея свободных денег, тем не менее изъявило желание приобрести наши программы. Котовскому лакокрасочному заводу (ЛКЗ – Тамбовская обл.) для производства нужна электроэнергия. Московскому энергетическому институту для ремонта аудиторий требуется краска. Нашей научной группе необходимо новое компьютерное «железо», инструментальные средства и, естественно, зарплата. Для решения подобных проблем человечество еще на заре цивилизации придумало деньги[13]. Переход же нашей страны от непонятно чего к рынку возродил натуральный обмен – бартер[14]. В вышеописанной товарной цепочке не хватало одного звена, чтобы она замкнулась. К счастью, в МЭИ поступила партия компьютеров, парочку которых мы договорились обменять на краску. В этой комбинации заключается только часть описываемого компьютерного

этюда, если вспомнить шахматное толкование слова «этюд» – решение головоломки путем составления цепочки ходов.

Вторая часть компьютерного этюда имела место уже в Тамбове и в Котовске – на ЛКЗ. В Тамбовэнерго мне (автор переходит к рассказу от первого лица) после сдачи программ выдали доверенность на получение лакокрасочной продукции на 14 млн., естественно, старых рублей в счет задолженности завода за электроэнергию и отправили в Котовск. В отделе сбыта ЛКЗ сначала наотрез отказались отпускать краску за какие-то там непонятные задолженности, а не за живые деньги, но после угрозы отключения света и тепла с трудом, но согласились. Краска, которая мне подходила[15], вернее не мне, а отделу снабжения МЭИ, стоила 14 600 рублей за литр и разливалась в тару (в барабаны, если следовать москательному жаргону, которого я нахватался в Котовске) объемом 15 и 55 литров. Пустые барабаны стоили 24 и 30 тыс. рублей соответственно. Работница отдела сбыта ЛКЗ (ее звали Оля), выписывая на компьютере накладную, спросила, в каких емкостях (пардон, барабанах) я возьму краску. Чутье давнего собирателя компьютерных этюдов сразу подсказало, что тут кроется типичная и, главное, реальная задача линейного программирования, где целевая функция, которую нужно максимизировать, – суммарный объем краски, переменные – количество наполненных краской барабанов по 15 и 55 литров, которые нужно забрать, и три ограничения – (1) стоимость краски не должна превышать оговоренных с Тамбовэнерго 14 млн. рублей, (2) нельзя брать неполную банку (ограничение на целочисленность

переменных) и (3) количество банок разной вместимости не должно быть отрицательными числами[16]. Оля вызвалась помочь решить эту оптимизационную задачу и тут же с помощью калькулятора[17]

прикинула, что мне нужно взять 16 больших и 2 маленьких барабана, вмещающих 910 литров краски на сумму 13 млн. 814 тыс. рублей. Вспомнив, как я отчаянно торговался в Тамбовэнерго и все-таки увеличил цену программ с 12 до 14 млн. руб., я спросил у Оли, а можно ли не терять 186 тысяч – не оставлять их Тамбовэнерго. Она сказала, что нет, так как такие задачи решает чуть ли не каждый день, оптимизируя не только стоимость краски, но и ее загрузку в контейнеры различной вместимости[18], и что она «собаку съела» на решении таких проблем.


Наблюдая за «танцем» Олиных пальцев на кнопках калькулятора и за числами на его дисплее, я понял, что Оля использует так называемый «рабоче-крестьянский» и, главное, ненадежный алгоритм оптимизации: сначала выбирается краска в большой таре, а затем остаток денег (или объема контейнера) заполняется краской в маленькой таре. Примерно так мы пакуем чемодан, отправляясь в поездку, – сначала кладем в него крупные вещи, а потом напихиваем в пустые пространства всякую мелочь. Еще раз вспомнив Вийона (смотри сноску 17), я спросил у Оли, почему она не использует для решения таких задач компьютер и табличный процессор Excel, рабочий лист которого как будто специально был выведен на экран ее компьютера. Я тут же вызвался показать, как это делается. В среде Excel есть так называемый Решатель (Solver), диалоговое окно которого вызывается командой Найти решение... из меню Сервис.

В этом окне пользователь указывает ячейку, хранящую целевую функцию, значение которой нужно максимизировать, ячейки с переменными поиска (в начале оптимизации они либо пусты, либо хранят значения первого приближения к максимуму) и ограничения.

Алгоритм оптимизации с помощью Решателя Excel можно назвать «ленивым»: пользователь формирует таблицу расчета и говорит: «По щучьему велению, по моему хотению сделай так, чтобы»... целевая функция приняла максимальное (минимальное, определенное) значение, но при этом были выполнены все ограничения». Для этого пользователю достаточно нажать кнопку Выполнить. Решатель Excel выдал нам старый результат – 16 больших и 2 маленьких барабана. Но сдаваться не хотелось.

Есть хорошее правило – проверять решение задачи не только другими методами, но и другими программными средствами. Кроме того, не следует забывать о KISS-принципе программирования. С поцелуями он ничего общего не имеет, хотя хорошее отношение к решаемой задаче и к компьютеру в нем просматривается. KISS – это аббревиатура английской фразы: «Keep It Simple, Stupid! – Делай это проще, дурачок!» Она призывает решать поставленную задачу наипростейшими способами и прибегать к изощренным алгоритмам и методикам только тогда, когда простые способы не годятся из-за длительности времени счета или из-за нерационального использования других ресурсов человека и/или компьютера[19].


Простейший способ решить на компьютере поставленную задачу – это перебрать

все варианты и остановиться на оптимальном. Благо вариантов не так уж много – 1088: на отпущенные 14 миллионов можно было взять не более 63 маленьких барабанов с краской или не более 16 больших [20]. Перебор можно назвать «компьютерно-рабоче-крестьянским» методом решения. Но помимо прочего он может дать стопроцентную уверенность не только в правильности, но и в единственности

найденного решения и даже показать, что таких решений несколько. А такая ситуация нередка в задачах целочисленного

линейного программирования.

Итак, перебор. Следуя вышеописанному правилу, новый метод решения задачи необходимо совместить с новым программным средством для его реализации. Это, конечно, можно было сделать и в среде Excel, составив таблицу всех решений и/или написав программу перебора на языке Visual Basic for Applications (VBA), встроенном в Excel. Но у Оли на компьютере был установлен еще и Mathcad (феномен рояля в кустах). Он довольно успешно решает задачи самого разного плана (включая и экономические) без обращения к чистому программированию (BASIC, C, Pascal и др.). Кроме того, в то время я работал над книгой, которую читатель держит в руках. Пример с краской эту книгу только украсит (нечаянный каламбур).

Задача о краске

Протокол «контрольного взвешивания» краски в среде Mathcad приведен на рис. 3.11. Комментарии поясняют, что происходит в формулах. Во-первых, функция Maximize, как и ожидалось, дала дробный ответ (см. пункт 2) – маленьких банок можно не брать, если можно брать дробное количество больших. Пришлось, вспомнив эпиграф и название этюда, перейти к перебору вариантов. В Mathcad-документе формируются две матрицы с именами Об (пункт 3.2) и Ст (пункт 3.3), элементы которых (их 1088 – у матриц 17 столбцов и 64 строки) хранят значения объема (Об) и стоимости (Ст) краски в зависимости от комбинаций расфасовки. Далее (пункт 3.4) некоторым элементам матрицы Об присваиваются нулевые значения, если данные комбинации расфасовки не проходят по стоимости. Остальное – ловкость рук и никакой математики: в пункте 3.5 определяется номер строки (переменная N_15) и номер столбца (N_55) матрицы Об, на пересечении которых находится элемент с максимальным значением. Ответ (6 маленьких барабанов и 15 больших) неприятно удивил Олю. Она невольно обманывала меня на 5 литров краски и на 139 тыс. руб.
Метод поиска координат точки максимума, реализованный на рис. 3.11 (двойная сумма), имеет существенное ограничение: в анализируемой матрице (у нас это Об) должен быть только один максимальный элемент. Если их несколько, то ответ будет неверен: в переменные N_15 и N_55 будут записаны суммы координат точек с максимальным элементом. Мы это наблюдали в пункте 2 на рис 3.9.
Так Mathcad сэкономил мне почти полторы сотни тысяч рублей. Деньги не такие уж большие, но если присовокупить к ним новый компьютерный этюд в книгу, новую тему лекции и новую лабораторную работу по информатике, а также гонорар за эту книгу, то игра стоила свеч.
Вернувшись из Тамбова домой в Москву, я в спокойной обстановке у своего родного компьютера еще раз проанализировал задачу. И вот что получилось.
Во-первых, заставить Решатель Excel правильно «разъяснять» задачу о краске можно было, изменив начальные установки Решателя. А для этого нужно было не полениться и нажать на кнопку Параметры... в диалоговом окне Поиск решения. В новом диалоговом окне Параметры поиска решения достаточно было допустимое отклонение уменьшить с 5 до 1%. После этого правильное решение (15 больших и 6 маленьких барабанов) было бы найдено. Честно говоря, в Excel плох не Решатель, а его начальные установки. Очень мало пользователей Excel, прибегающих к услугам Решателя, нажимают кнопку Параметры... Тот же, кто разбирается в сути установок оптимизации, как правило, с Excel не работает. Отсюда и недоразумения.

Во-вторых, и Оля, и Excel, и Mathcad в разной степени меня немножко обманули[21]: 910 литров краски можно было отгрузить и другим вариантом – 13 маленьких и столько же больших барабанов[22]. В этом случае осталось бы «сдачи» всего 12 тыс. рублей. Более того, решение задачи о краске с новой целевой функцией (стоимость краски в банках) дает еще один результат: 37 маленьких и 6 больших барабанов, выбирающий еще одну тысячу из Тамбовэнерго.

Вариант расфасовки (число маленьких барабанов/число больших барабанов)	2/16	6/15	13/13	37/6
Объем краски (л)	910	915	910	885
Остаток невыбранных денег (руб.)	186 000	47 000	12 000	11 000

В-третьих, когда я показал эту таблицу в отделе снабжения МЭИ, то мне было сказано, что самый оптимальный вариант и для меня (мне важны деньги) и для МЭИ (ему нужна краска) четвертый: у Тамбовэнерго были бы выбраны почти все деньги, а 885 литров краски, как это ни кажется странным, больше, чем 910 и 915. Дело в том, что при крупной расфасовке много краски теряется из-за переливов в меньшую тару. 15-литровый барабан можно взять в ремонтируемую аудиторию и там полностью использовать.
Неверное решение задачи получается не только из-за плохих методик или дефектных программных средств, но и из-за того, что пользователь сам толком не знает, чего он хочет. Все программы решения задачи линейного программирования требуют четкого формулирования одной единственной целевой функции[23]. При решении учебных задач цель ясна. А что является целью в жизни? Но это уже не математика, а философия...
У метода перебора, реализованного на рис. 3.11, есть три собственных ограничения:
1) число переменных не может быть больше двух, так как в среде Mathcad есть векторы и матрицы, но нет тензоров (трех- и более мерных матриц);
2) при чрезмерном размере матрицы компьютер отказывается иметь с ней дело, выдавая протестующее сообщение типа «не хватает памяти»;
3) счет (если перебор можно назвать счетом) может длиться нестерпимо долго.
Первые два ограничения снимаются при переходе от метода формирования матрицы (рис. 3.11) к методу перебора вариантов с запоминанием только оптимального плана, который можно реализовать средствами программирования, что мы и сделаем в этюде 6 (см. рис. 6.31 и 6.32).
Метод перебора оказывается незаменимым (то есть опять же бывает не таким уж извращенным), когда задача, оставаясь целочисленной, теряет свою линейность[24]. В этом случае традиционные методы (например, симплекс-метод) часто оказываются бессильными.
Тем не менее реализация метода перебора в среде Mathcad всегда будет извращением чистой воды. Mathcad – это программа интерпретирующего типа с низкой скоростью выполнения исходного текста. Для перебора нужны не просто компиляторы, а компиляторы, оптимизирующие время выполнения программы.

Поиск места для ларька

На рис. 3.12 помещен протокол решения задачи о поиске места для ларька на дачном участке. Критерий поиска – минимум суммы расстояний от ларька до всех остальных домиков. Их координаты X и Y – случайные числа в интервале от 0 до 20 (наша задача учебная). Ларек может быть либо встроен в один из домиков (пункт 1), либо стоять отдельно (пункт 2). На рис. 3.12 координаты встроенного ларька определяются перебором. Затем эти координаты (Xiопт и Yiопт) становятся первым приближением для уточнения местоположения отдельно стоящего ларька. Заканчивается расчет графическим описанием и сути и решения задачи. Здесь главное – правильно отформатировать точки на графике. Поэтому выведено окно форматирования графика.
Вернемся к тестовым задачам на рис. 3.3-3.5.
На рис. 3.3 и 3.4 формируются матрицы М, элементы которых – значения анализируемых функций в узлах сетки, накрывающей точку минимума. Элементы матрицы М средствами Mathcad превращаются в линии уровня и в поверхность. Но эти матрицы могут сослужить нам и другую службу – координаты их минимальных элементов могут стать точками первого приближения к минимуму. Нащупать минимум (максимум) функции более чем двух аргументов (например, функции Пауэла – см. рис. 3.5) можно средствами программирования (см. этюд 6).
Транспортная задача, решенная нами на рис. 2.10, кочует из одного учебника в другой. Везде отмечается такой ее парадокс – по самому дешевому маршруту при минимизации затрат на перевозки ничего не возится. Если бы мы решали эту задачу вручную без компьютера, то сначала полностью загрузили бы дешевый маршрут, а потом все остальные. Этим парадоксом может воспользоваться хозяин транспортного предприятия, максимизировав свою прибыль от перевозок (см. рис. 3.13):

Транспортная задача (извращенное решение)

В этом случае второй по дороговизне маршрут (1200 у.е.) остается свободным – внешне все выглядит прилично.
Но парадокс задачи не в этом. Вернее, не только в этом. Дело в том, что она недостойна не только функций Minimize и Maximize, но даже и грубого перебора, так как сводится к решению простейшего уравнения:
с1м1+с2м1=40
Если с1м1=0, то с2м1=40, и затраты на перевозки максимальны. Если с2м1=0, то с1м1=40, и затраты максимальны. Рис. 2.10 и 3.13 – это чистой воды извращения. Или неумение либо нежелание подумать как следует над задачей.

Логические операторы и функции

Во-первых, булевы функции в среде Mathcad можно определить. Математика (см., например, «Справочник по математике для научных работников и инженеров» Корн Г. и Корн Т.) оперирует одной
одноместной (с одним аргументом) и семью
двухместными (с двумя аргументами) булевыми функциями. Все они определены в пунктах 0-7 на рис. 3.14. Если булеву переменную уподобить выключателю с двумя позициями («вкл» и «выкл»), то конъюнкция
– это последовательное соединение выключателей (пункт), а дизъюнкция – параллельное. Электрический аналог эквиваленции (пункт 3) может очень пригодиться для освещения длинного коридора, свет в котором зажигается и тушится независимо в двух его концах двумя выключателями.
В пункте 8 на рис. 3.14 сформирована трехместная булева функция с именем Решение, возвращающая вердикт жюри из трех человек: решение проходит, когда «за» голосуют двое или трое. Воздерживаться или уклоняться от голосования нельзя.
Функция Решение (программная реализация процедуры голосования) в пункте 8 на рис. 3.14 также имеет электрический аналог (аппаратная реализация – машинка для голосования) – комбинацию выключателей, соединенных последовательно и параллельно.
Двухместные булевы функции (пункты 1-7 на рис 3.14) имеют четыре (22) комбинации значений аргументов (таблица истинности), трехместные – уже 8 (23), одноместная, естественно, только две (21) – 0 или 1. Самих же двухместных булевых функций может быть 16 (42 – мы описали только семь), трехместных уже 64 (43 – мы описали только одну). Одноместных булевых функций четыре (41 – мы описали только одну). Вот другие три одноместные булевы «функции» y2(x):=1, y3(x):=0 и y4(x):=x. Но никакой практической ценности в программировании они не имеют: первые две (y2 и y3) – это константы, а y4 – это просто сам аргумент. Ненаписанные нами остальные девять (16-7) двухместные булевы функции (там тоже есть константы) имен не имеют и, как правило, ни в математике, ни в программировании не применяются.
В математике булева функция выдает два значения (0 – 1, да – нет, истина – ложь и т.д.), в программировании же – минимум три: да, нет и... аварийный останов, связанный с ошибкой (один или несколько аргументов не определены). Такую ошибку можно обработать (в Mathcad для этого служит оператор on error) и пустить расчет по третьему пути. Одноместных булевых функций может быть больше четырех. Как понравится такая функция: y5(x):=if(rnd(1)>0.7, 1, 0), возвращающая единицу с вероятностью 30%, и нуль – с вероятностью 30%.

Функцию Решение можно построить намного проще – вычислить среднее арифметическое значений аргументов. Эту работу выполняет встроенная Mathcad-функция mean. Если оно окажется больше, чем 0.5 – то решение принято (возвращается единица), нет – нуль:

Решение(V):= mean(V) > 0.5

Число аргументов новой функции Решение, таким образом, допустимо увеличивать, не прибегая к сложному дереву булевых операций, показанных в пункте 8 на рис. 3.14.

В пункте 9 на рис. 3.14 формируется еще одна функция Решение для голосования комитета с любым числом членов, принимающих решение большинством голосов. Но при этом часть голосующих обладает правом вето

(пример – Совет Безопасности ООН где, как писал Джорж Оруэл: «все равны, но некоторые равнее»). Люди (или страны: США, Россия, Китай, Франция и Великобритания, если иметь в виду СБ ООН) с правом вето у нас объединены в вектор Const (постоянные члены СБ), а все остальные – в вектор Var. Если для принятия решения большинством голосов годится среднее арифметическое, то для блокировки принятия решения – среднее геометрическое (gmean): корень n-й степени из произведения n сомножителей. Эта встроенная функция появилась только в восьмой версии Mathcad. При этом gmean требует, чтобы все элементы вектора (матрицы) аргумента были ненулевыми. Поэтому в пункте 9 на рис. 3.14 мы сначала переопределили функцию gmean так, чтобы она «проглатывала» и нулевые элементы вектора-аргумента, а потом уже с ее помощью сформулировали функцию Решение для электората типа СБ ООН. В конце пункта 9 показаны три типичных исхода голосования:

— решение принимается большинством голосов;

— решение проваливается одним человеком с правом вето;

— решение не проходит, так как большинство против.

Конечно, использование среднего геометрического для подсчета голосов – это чистой воды извращение (см. название данного этюда). Тут можно использовать функцию And – просто логическое умножение безо всякого корня. В пункте 10 на рис. 3.14 сформулированы функции And и Or, аргументы которых – векторы-столбцы с переменным числом элементов[26].


Этой главке автор хотел дать и другое название – «Казнить нельзя помиловать». Но уж больно оно избитое. Традиционно читателя просят поставить запятую в этом предложении[27]

и проследить, как меняется смысл вердикта в зависимости от места такого невинного знака препинания.

А как вам понравится такой ответ на вопрос о месте запятой: запятую нужно «размазать» по предложению – n процентов запятой поставить после слова «казнить», а 100-n – после слова «нельзя». Трактовать такую новую грамматическую (пунктуалистическую?) конструкцию можно по-разному. Но сначала поговорим о самой постановке вопроса.

Один лидер «третьего рейха» любил повторять, что он всегда хватается за пистолет, слыша слово «культура». Сталкиваясь с логической задачей, программисты «хватаются» за троицу булевых функции Not, And, Or и т.д. Но их-то и нет в списке встроенных

функций Mathcad. Нет там и булевых (логических) переменных. Тут программист чертыхнется (а зря – см. ниже) и напишет соответствующие пользовательские функции (см. пункты 0 – 7 на рис. 3.14), заставляя числовые[28]

переменные выполнять по совместительству и роль булевых. После этого ничего не стоит написать булеву функцию Решение, возвращающую единицу

(логическое «Да») или нуль («Нет») в зависимости от итогов голосования – решение принимается, если двое или трое присяжных проголосуют «За».

Возвращаясь к дилемме «казнить-помиловать» и допуская совмещение должностей присяжного, судьи и палача, можно попытаться заменить в схеме пункта 8 электрическую лампочку на... электрический стул. Говорят, что подобная схема рубильников на самом деле запитывает американское орудие казни. Каждый из трех, приводящих приговор в исполнение, надеется, что он включил не настоящий рубильник, а муляж рубильника.

Еще немного об «электрических цепях». Последнее время в быту получают распространение выключатели, плавно меняющие накал лампочек от нуля до ста процентов. Еще раньше такие устройства (реостаты) стали применяться в театрах и кинозалах. Медики уверяют, что плавный переход от света к темноте через полумрак благотворно влияет на зрение.


А можно ли подобными регуляторами заменить выключатели в вышеприведенной схеме аппаратной реализации процедуры голосования? Может ли функция Решение иметь не только логические, но и вещественные аргументы и возвращать вещественное значение, плавно меняющееся от нуля до единицы (от 0 до 100%)? Очень часто, осуждая или оправдывая кого-либо, трудно прийти к однозначному решению. Даже на первый взгляд явное преступление может иметь такую оценку – «это скорее беда, чем вина подсудимого». Но людей, принимающих решения, по-прежнему заставляют давать только черно-белые оценки[29].

Толерантность[30]

сначала проникла в религию. Человечество, нахлебавшись крови в религиозных войнах[31], относительно поумнело. Сейчас цивилизованный человек может сказать о себе, что он на k процентов атеист, на l процентов мусульманин, на m процентов – католик, а на n процентов – протестант (гугенот – вспомним Варфоломеевскую ночь и Париж, который стоил мессы). И не обязательно, чтобы k+l+n+m равнялось ста процентам. Во многих церквях Америки по пятницам служит мулла, по субботам – раввин, а по воскресеньям – священник (поп, пастор, ксендз) и никого это не шокирует. Затем толерантность охватила мир искусства, размыв систему классических канонов и стилей. Сейчас главное – это талант художника и то, что он хочет сказать миру. И не важно, кто он – реалист, импрессионист (нео-, пост- и т.д.) или просто примитивист, впервые взявшийся за кисть в 70 лет. Теперь стали говорить и о терпимости в науке. Ее проявления – теория нечетких множеств

(fuzzy sets – см. рис. 6.41-6.45 в этюде 6) и теория нечеткой логики (fuzzy logic). Неоднозначность оценок стала превалировать не только в гуманитарных дисциплинах (см. сноску 27 с деликатной подсказкой Word’а), но и в точных науках – в математике, например. Автор где намеренно, а где по незнанию (по недопониманию – хороший пример нечеткого множества в живом языке) не совсем верно трактует положения теории нечетких множеств. Раньше бы такого автора с кашей съели. А теперь ничего – публикуют, читают.


Но это, конечно, не значит, что размываются все грани черно-белых оценок. Об этом хорошо сказано у Пушкина:

Ах! Чувствую: ничто не может нас

Среди мирских печалей успокоить;

Ничто, ничто… едина разве совесть.

Так здравая она восторжествует

Над злобою, над темной клеветою. –

Но если в ней единое пятно,

Единое, случайно завелося,

Тогда – беда! Как язвой моровой

Душа сгорит, нальется сердце ядом,

Как молотком стучит в ушах упрек,

И все тошнит, и голова кружится,

И мальчики кровавые в глазах…

С другой стороны у Ф.М.Достоевского в «Скверном анекдоте» читаем: «Был он и честен, то есть ему не пришлось сделать чего-нибудь особенно бесчестного…».

Давайте посмотрим, как нашу задачу о голосовании можно решить с учетом положений теории нечеткой логики (пункт 10 на рис. 3.14). Задачу можно обогатить элементами нелинейности, приняв во внимание условное деление голосующих на консерваторов (k), традиционно склонных к осуждающим приговорам, центристов (c) и либералов

(l – эль). Степень радикальности жюри присяжных (парламента и вообще любого электората) будем учитывать через коэффициент k. Голосующие устанавливают степень своего решения «за» (от 0 до 1), но на исход голосования влияют функции yk, yc и yl, демпфирующие крайние оценки (см. пункт 10.1).

«Цветная» функция Решение, построенная на функциях min и max (см. пункт 10.2), при логических значениях аргументов (0 или 1) полностью эквивалентна своему «черно-белому» аналогу, использующему функции And и Or (см. пункт 8). Встроенные функции min и max способны работать и с логическими, и с вещественными, и даже с комплексными[32]

аргументами. Кроме того, функции min и max удобны еще и тем, что их аргументами может быть вектор-столбец (аргумент функции max в пункте 10.2), вектор-строка (min) и даже матрица (см. рис. 6.34 в этюде 6). Это позволяет комбинировать типы аргументов (горизонталь-вертикаль) создаваемой «цветной» логической функции, делая ее более компактной и более легкой для понимания. (Здесь вызывается не функция, а постфиксный оператор – это позволяет убрать лишние скобки.)


Ладно, скажет читатель, а что делать с вердиктом присяжных такого рода: «Виновен на 57%, невиновен на 43%»? Что делать? Смотреть на графики, материализующие «цветное» решение!

В пункте 10.2 на рис. 3.14 визуализированы вердикты присяжных при фиксированном решении либерала 0.5 (воздержался – ни то ни се).

Интерпретация цвета участков поверхности решения (здесь, к сожалению, не цвета, а оттенки серого) может быть такая:

красный цвет графика говорит сам за себя – кровь, «вышка»;

оранжевый – пожизненное заключение;

желтый – каторга;

зеленый – тюремное заключение;

голубой – условное осуждение;

синий – общественное порицание;

фиолетовый – невинен.

Цветовую палитру («Каждый охотник желает знать, где сидят фазаны!») можно сдвигать, учитывая тенденции в общественном сознании и изменения в законодательстве – мораторий на смертную казнь, например. При этом нужно будет «сдвигать вниз» (в холодные тона) и другие виды наказаний. В наших тюрьмах условия содержания такие, что смертная казнь может оказаться просто наградой. Основной довод противников смертной казни в том, что жизнь – это Дар Божий, и только всевышний может приговорить к высшей мере. Но и свобода не меньший дар! Второй довод в том, что смертная казнь делает невозможным исправление судебных ошибок. Но. Отсидел человек 20 лет в камере пожизненного заключения, а ему говорят, пардон, мы ошиблись. Кто вернет загубленную жизнь.

Строить «цветные» логические схемы поможет и нечеткая функция Not:

Not(x):=½1-x½ или ½100-x½.

В пункте 10.3 на рис. 3.14 функции max и min заменены на их «аналоги» – на функции mean (среднее арифметическое) и gmean (среднее геометрическое). Поверхность стала более гладкой – природа, как мы знаем, не терпит острых углов.

В пункте 11 на рис. 3.14 сформированы многомерные функции And и Oг. Но записать допустимо еще проще:

And(x):=min(x)          Or(x):=max(x),

А можно работать только с min и max, которые хорошо справляются и с булевыми (четкая логика), и с вещественными (нечеткая логика) аргументами. Но если пользователь оптимизирует программу (см. главку 6.12), то вместо функции min лучше использовать оператор умножения. Дело в том, что при умножении сразу возвращается нуль, если первый сомножитель нулевой. Функция же min излишне педантична – она перебирает все элементы своего аргумента-матрицы (вектора).

Но увлекаться статистическими функциями (min, max, mean, gmean, rnd, var и др.) при реализации логических схем нужно осторожно. Уинстон Черчиль говорил, что есть Большая Ложь, Просто Ложь и… Статистика – героиня этого этюда.

BASIC-программа поиска корня уравнения

Проанализировав эту программу, можно понять, почему корнем другого уравнения Y = X2 - 4 при нулевом (симметричном – проблема Буриданова осла) начальном приближении оказывается плюс, а не минус 2:
x := 0          x := root(X2 - 4, X)    x = 2
Хотя в BASIC-программе полностью реализован метод секущих, описанный в Руководстве пользователя, но...
Во-первых, в вышеприведенную BASIC-программу не заложено никаких сообщений об ошибках, а функция root его выдает (см. пункт 5 рис. 3.1). Во-вторых, BASIC-программа, в отличие от функции root, прекрасно нашла корень уравнения y(x), заданного в пункте 1, от начального приближения, равного плюс 5. И, в-третьих, в BASIC-программу заложен не метод секущих, а комбинированный метод Ньютона-секущих. Классический метод секущих требует задания не одного, а двух начальных значений аргумента: через одну точку проводится касательная (метод Ньютона), а через две – секущая. Вот так мы разобрались с функцией root! Хотели над ней подшутить, а она сама над нами посмеялась.
В этюде 6 читатель может найти функции пользователя для поиска корней уравнений методом Ньютона, методом половинного деления и методом секущих, ориентированные по точности не на значение анализируемой функции (Do ... Loop Until Abs(FnY(X1)) <= TOL – см. программу на рис. 3.2), а на значение аргумента (Do ... Loop Until Abs(X1 – X0) <= TOL, например). На такую подмену приходится идти, решая реальную задачу. Так, например, в коллекции автора есть учебная программа определения значения рН раствора, где рН ¾ это корень уравнения электронейтральности раствора (баланс катионов и анионов). Но нас мало интересует дисбаланс ионов (отклонение анализируемой функции от нуля) ¾ главное, чтобы новое значение рН отличалось от предыдущего не более чем на величину 10-3
(обычная точность рН-метра).

Поиск минимума у двухмерной экспоненциальной функции

Двухмерная экспоненциальная функция имеет минимум (нулевое значение) при x=1 и y=10. Это хорошо видно в пункте 1 на рис. 3.3, где показаны поверхность и линии уровня вблизи минимума[2]. Эти графики несложно построить, если, конечно, знаешь, где находится минимум, охватываемый переменными x1, x2, y1 и y2. Поверхность развернута так (см. ее координаты на фрагменте окна редактирования), чтобы линии уровня являлись проекцией поверхности на горизонтальную плоскость.
В пункте 2 при поиске минимума в качестве начальных приближений давались точки, расположенные по углам прямоугольника ¾ области существования аргументов на графиках. Так испытывалась сходимость метода поиска минимума. Зафиксирована всего лишь одна осечка: при начальном приближении x=1.2 и y=14 не был найден корень системы, состоящей из приравненных к нулю частных производных двухмерной экспоненциальной функции[3].

Функция «Победитель»

Что происходит в функции Победитель?
В начале дуэли все участники живы: все три элемента вектора Статус принимают значение “жив”[50]. Далее проводится жеребьевка: определяется направление очередности выстрелов (если переменная Очередь равна единице, то очередность идет в таком направлении ...0®1®2®0®1®2.., если минус единице – ...0®2®1®0®2®1) и определяется первый стреляющий (переменная Стрелок). Кроме того, обнуляется переменная Убийство, по которой прерывается цикл выстрелов в дуэли.
Математическая модель дуэли опирается на цикл с выходом из середины (while ... break…): дуэль продолжается, пока не будут сделаны два результативных выстрела. В теле цикла while определяется Цель – самый меткий противник, которого убивают (СтатусЦель
¬ “убит”), если, во-первых, не промахиваются (МеткостьСтрелок
> rnd(1)) и (And), во-вторых, не (Not) стреляют намеренно в воздух. Второе имеет место при хитрой тактике стреляющего (ТактикаСтрелок = 2) и (And), если метких противников более одного.
Определение следующего стреляющего ведется в цикле с постпроверкой (while ... break): цикл прерывается, когда, перебирая очередь, отмеченную выше (...0®1®2®0®1®2.. или ...0®2®1®0®2®1...), «натыкаются» на живого участника.
Возвращает функция Победитель номер участника дуэли (0, 1 или 2), оставшегося в одиночестве (значение переменной Стрелок по выходу из цикла).
Функция Победитель возвращает непредсказуемое целочисленное значение 0, 1 или 2, так как в ней в трех местах вызывается встроенная в Mathcad функция rnd, которая возвращает псевдослучайное число в интервале от нуля до значения аргумента функции rnd. Этот аргумент у нас равен либо единице (случайный выбор очередности выстрелов и имитация выстрела с вероятностью попадания, пропорциональной меткости стреляющего), либо трем (случайный выбор первого стреляющего – здесь дополнительно работает встроенная функция floor, возвращающая у положительного вещественного числа его «пол» (в смысле не «потолок» – по-английски a floor): floor(0.54), floor(1.82), floor(2.48) = 0...

Поиск минимума у функции Розенброка

Функция Розенброка примечательна тем, что ее минимум невозможно увидеть ни на линиях уровня, ни на поверхности (пункт 1 на рис. 3.4). Скажем осторожнее – автору не удалось этого сделать. На графиках просматривается типичный овраг, где анализируемая функция в одном направлении изменяется круто, а в перпендикулярном – слабо. Этим пытаются как бы дезориентировать программу поиска минимума – на то и создаются тестовые функции. Графики строились по новой, третьей технологии ¾ задавался центр (x и y) квадрата со стороной 2D области существования аргументов на графиках. Вторая технология ¾ это когда задаются координаты углов прямоугольника существования аргументов на графиках (см. пункт 1 на рис. 3.3). Первая технология (кстати, самая неудобная для понимания) была использована, например, в рис 2.8 – там область размаха поверхности завуалирована в значениях переменных i и j.
В пункте 2 на рис. 3.4 поиск минимума велся от трех начальных точек (10-10, 100-10 и 100-100) тремя способами. Итоги «соревнования»: на первом месте по-прежнему функция MinErr, которая выдавала абсолютно точный результат (пару единиц). На втором месте функция Minimize c относительно правильными ответами. Функция же Find сошла с трети дистанции – только при первом приближении был выдан относительно точный результат. Здесь, по-видимому, с функцией Find овраг сыграл злую шутку.
Функция Розенброка имеет минимум (нуль) при x=1 и y=1. Через эту точку можно провести секущие плоскости и показать на декартовых графиках, что функция там минимальна (см. пункт 3 на рис. 3.4), ее частные производные равны нулю, а частные производные второго порядка положительны.

Поиск минимума у функции Пауэла

Функция Пауэла (рис. 3.5) имеет четыре аргумента. Следовательно, в трехмерном мире – даже виртуальном – никакими поверхностями и линиями уровня минимум (нуль) функции Пауэла не локализовать (не визуализировать). Проверить соответствие найденной точки (четыре нуля) минимуму можно либо через декартовы графики сечений по технологии рисунка 3.3), либо через линии уровня, что и было сделано в пунктах 2.1 и 2.2 на рис. 3.5. Для этого две координаты фиксируются на нулевых значениях, а две другие изменяются вокруг нуля (нули – это координаты минимума). Таких топограмм четырехмерной функции можно построить шесть штук следующих пар аргументов: a0-a1, a0-a2 (см. рис. 3.5), a0-a3, a1-a2, a1-a3 и a2-a3 (по четырем последним парам читателю предлагается построить топограммы самому). Решение по функции Пауэла более-менее удачно велось с помощью функций MinErr и Minimize. Поиск корня системы четырех алгебраических уравнений – частных производных функции Пауэла – здесь применить нельзя, так как переменные анализируемой функции у нас не скалярные величины (с именами a, b, c и d, например), а одиночная переменная-вектор с именем a. По индексным переменным производная в среде Mathcad не высчитывается. Читатель при желании может переопределить функцию Пауэла (задействовать в ней четыре переменные-скаляра) и решить задачу с помощью частных производных. Так, кстати, решалась эта задача в предыдущих изданиях книги.
Выводы по испытаниям трех функций – в конце этюда.

Подсчет числа p методом Монте-Карло

Есть более простой способ статистического расчета числа p, чем тот, который использовал Бюффон. Можно нарисовать квадрат, вписать в него круг («квадратура круга») и бросать туда камешки. Так как в площади круга запрятано число p («пи эр в квадрате» – вспомним старый анекдот о том, почему у поезда колеса стучат), то через подсчет попаданий в круг можно оценить число p. Бюффон этот метод не использовал наверное из-за того, что трудно добиться равномерного попадания камешков в квадрат.
На рис. 3.6 зафиксирована оценка площади круга, вписанного в квадрат, и сделана попытка расчета значения числа p. Как это делалось?
В пункте 1 на рис 3.6 формируются два вектора X и Y, элементы которых (а их 7000) ¾ случайные вещественные числа в интервале от минус до плюс единицы. X и Y – это по своей сути координаты точек случайного падения камешков в квадрат размером 2 на 2. Далее в пункте 2 эти камешки сортируются на «чистых и нечистых»: координаты точек, попавших в круг, дублируются в векторах Xo и Yo (o ¾ попал), а не попавших ¾ в векторах Xx и Yx (x ¾ промах). После этого несложно визуализировать попадание точек в круг с помощью параметрического декартового графика. Достаточно при форматировании графика указать, что линий нет, а есть одни точки. При этом точки, попавшие в круг (вектора Xo и Yo), более толстые. Теперь для оценки числа p можно подсчитать число попаданий камешков в круг (пункт 4) ¾ число ненулевых элементов вектора Xo (или Yo). В пункте 5 число p рассчитывается и сравнивается с его точным значением.
Функция rnd в среде Mathcad имеет аргумент, отличающийся от своих аналогов на языках программирования. В среде BASIC или Pascal аргумент функции rnd связан с приставкой псевдо- в ее названии, а не с диапазоном генерируемых случайных чисел. Да, числа генерируются случайные, но ряд этих чисел псевдослучаен, так как его в любой момент можно повторить. За такой повтор на языках программирования отвечает аргумент функции rnd, а в среде Mathcad – число (по умолчанию это 1), хранящееся в окне Seed value for random numbers (инициализация генератора случайных чисел) ярлыка Built-in Variables окна Math Options, которое вызывается на дисплей командой Options в меню Math:



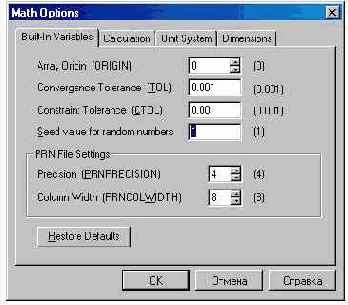
От истинно случайных чисел отказались еще на заре развития компьютерной техники, когда пытались встраивать в ЭВМ что-то похожее на рулетку. Но это устройство оказалось слишком неповоротливым, а главное, с его помощью невозможно было получать повторяющиеся ряды случайных (псевдослучайных) чисел, что необходимо при отладке программ. Поэтому генерированию случайных чисел на физических моделях (рулетка) предпочли их математическое моделирование. Какой алгоритм заложен в функцию rnd, пользователя волнует мало – главное, чтобы ряд генерируемых чисел не вырождался, а сами числа распределялись в заданном диапазоне равномерно[4], в чем можно убедиться визуально – см. пункт 3 рис. 3.6.

Наш подсчет числа p методом Монте-Карло (а рулетка была не зря упомянута) – это чистой воды извращение (пардон, деривация): то же число p (или интеграл) легко можно рассчитать напрямую – конец пункта 5. Но все-таки наше извращение было не таким уж извращенным.

Во-первых, решив задачу на рис. 3.6, мы, по сути, не рассчитали значение p, а проверили качество генератора псевдослучайных чисел, то есть добротность встроенной функции rnd. При числе бросаний «камешков в воду», стремящемся к бесконечности, ошибка метода Монте-Карло должна стремиться к нулю, если функция rnd работает правильно.

Во-вторых, есть фигуры, площади которых невозможно рассчитать традиционными методами, без «извращений». Пример – площадь облака на снимке из космоса. Эту площадь довольно точно и, главное, быстро (в метеорологии вчерашний прогноз никому не нужен) можно определить, ткнув случайным образом несколько раз в фотографию иголкой, и… см. рис. 3.6.

Традиционные способы подсчета площади фигуры (интеграла) тут не годятся не только потому, что контуры облака невозможно описать какой-либо интегрируемой функцией, но и из-за того, что они размытые, нечеткие.

В математике, самой точной на свете науке, появилось новое направление: теория нечетких множеств (другой термин – «размытые множества», но по-английски это звучит более поэтично: «fuzzy sets» – пушистые множества[5]). Эта теория оперирует такими «перлами», как «скорее 1, чем 2», «скорее плюс, чем минус», «точка находится скорее под графиком, чем над ним» и т.д. В основе теории нечетких множеств лежит знаменитый софизм: «Если к горсти зерна добавить еще одно зернышко, превратится ли она в кучу? А если добавить два зерна? А сколько зерен превратят горсть в кучу?» Это самое сколько


– типичный представитель fuzzy set, к которому трудно приложить и современную теорию чисел, и саму цифровую вычислительную технику. Программирование же – это по своей сути жонглирование нулями и единицами, то есть крайняя категоричность мироощущения, когда все богатство цветов и оттенков сводится к черному и белому. Мир же состоит не из чисел, а из куч, горстей, облаков, то есть из нечетких множеств, к обсчету которых современные компьютеры приспособлены очень плохо. Кто поднимался на самолете сквозь облака, знает, что никакой границы между облаком и не облаком нет. В этом-то, по-видимому, и будет заключаться один из будущих кризисов теории программирования и вообще элементной базы компьютеров. К теории нечетких множеств мы еще вернемся в конце этого этюда в главке о четкой и нечеткой логике и в этюде 6. А пока задание читателю – реализовать в среде Mathcad метод подсчета числа p, предложенный Бюффоном.

Поэтому повторяю – наше извращение на рис. 3.6. было не таким уж извращенным.

Можно сказать, что на рис. 3.6. мы, подражая Казимиру Малевичу, нарисовали «Черный круг в черном квадрате». Так мы невольно вторглись в Мир Искусства…

Считается, что искусство зиждется на трех китах. Вот они: чувство меры, воображение и ... потребность в извращениях, связанная с сомнениями и творчеством.

Теперь о сомнениях.

Подсчет объема конуса

На рис. 3.7 не только рассчитан объема конуса методом Монте-Карло, но и дано изображение самого конуса. В изобразительном искусстве есть направление, называемое пуантилизм
(от французского pointiller – писать точками). Его последователи формируют картину отдельными мазками правильной точечной или прямоугольной формы. Мы уже нарисовали в такой манере «Черный круг в черном квадрате». «Натюрморт с конусом», выполненный в этом же стиле, можно увидеть в пункте 3 рис. 3.7. Здесь «поработал» Scatter Plot – трехмерный точечный график. Так незаметно мы перешли от двухмерной к трехмерной графике – от живописи к… скульптуре.
Рисовался (вернее, ваялся) конус так. В прямоугольный параллелепипед размером 2 на 2 на 1 бросались случайным образом «камешки» – формировались три вектора X, Y и Z, элементы которых – случайные числа в диапазоне минус единица – плюс единица (векторы X и Y) и ноль – единица (вектор Z см. пункт 1 на рис. 3.7). Далее точки, не вписывающиеся в конус, отсеивались: соответствующим элементам вектора Z присваивалось значение бесконечности (пункт 2), и они... «улетали на небо», формируя линию над конусом (пункт 2).
Пункты 3 и 4 – это подсчет объема конуса методом Монте-Карло и сравнение его с истинным объемом конуса[6]. Сомнения остались, но очень незначительные – в пределах ошибки метода Монте-Карло.
Один великий художник сказал, что ваять очень просто – берется глыба мрамора и от нее отсекается все лишнее. «Всякий талант неизъясним. Каким образом ваятель в куске каррарского мрамора видит сокрытого Юпитера и выводит его на свет, резцом и молотом раздробляя его оболочку?»[7]
А вот еще одно парадоксальное высказывание: «Играть на фортепиано очень просто. Достаточно в нужный момент нажимать нужные клавиши!» Все это можно рассматривать как некую браваду или как попытки Художника подурачить публику, пристающую с «глупыми» вопросами о тайне творчества. А можно принять за руководство к действию. С живописью мы разобрались (см. рис. 3.6) – возьмемся теперь за скульптуру.
На рис. 3.7 у нас есть «глыба мрамора» размером 2 на 2 на 1, от которой также отсекается лишнее (осколки падают не на пол, а улетают на небо). Пока у нас «изваялся» простой конус, но ничто не мешает нам усложнить формулы в пункте 2 на рис. 3.7 и слепить Венеру Милосскую или Мыслителя Родена… На рис. 3.8 дается методика ваяния человеческой фигуры.

Ваяние на компьютере

Автор пока поступил проще. Он через команды форматирования графика окрасил точки конуса на рис. 3.7 в зеленый цвет, подбросил еще несколько точек красного цвета и большего диаметра. Поучилась неплохая новогодняя елка.
Сейчас компьютер широко используется как рабочий инструмент художника (интеллектуальная кисть или что-то в этом роде). Распечатки цветных принтеров оправляются в рамки и выставляются в, так сказать, реальных и виртуальных компьтерно-художественных салонах (см., например, журнал «КомпьюАрт»).
Но автору хотелось бы обратить внимание уважаемых читателей на другое – на проблему эстетического вида не просто компьютерных рисунков, а листингов программ и, в частности, на проблему соответствия (или противопоставления) формы листинга содержанию программы.
Программисты, которым не чуждо образное мышление, давно уже подметили, что процедуры и функции имеют свое собственное «лицо», по которому она безошибочно узнается на экране дисплея или на бумаге принтера. Одна процедура как ухоженная крестьянская лошадка круглая и гладкая – работает себе спокойно, перекачивая, например, данные из одного формата в другой. И внешне она неприметна –  взгляд на ней не останавливается. Другая процедура все время норовит выкинуть какой-нибудь фортель, настолько она неотлаженна (необъезженна). И своими очертаниями она походит на скакуна, в седле которого сидит герой многочисленных живописных полотен и скульптур. Третья процедура так и просится, чтобы ее оправили в раму и повесили на стену, настолько она хороша и закончена, а главное, ее форма полностью отвечает ее содержанию. Она передает не только мысли, но даже и настроение
художника, пардон, программиста, ее создавшего.
Автор далеко не искусствовед и не смеет особо распространяться на эту тему.
В комментариях к публикуемым компьютерным рисункам, как правило, подчеркивается, что их авторы – компьютерные художники. В прилагательных к существительным очень часто таится некая ущербность или по, крайней мере, двусмысленность: не просто математика, а «Прикладная математика» – см. главку «Mathcad и Maple» в этюде 7. Термин компьютерный художник

содержит в себе некую двойственность. С одной стороны, прилагательным «компьютерный» как бы извиняются перед потенциальным зрителем за эстетику рисунков (см. наши «рисунки» 3.6 и 3.8). А с другой стороны – предупреждают о том, что при создании рисунков использовались специфические инструменты и методы (авангардистские изыски).

Настоящий художник готов работать на чём угодно и чем угодно. Рисунки Анатолия Зверева (художника с трагической судьбой, какая, увы, часто постигает гениев), выполненные чуть ли не окурком на обрывке листа бумаги, продаются на аукционах за большие деньги. Давайте дождемся времен, когда распечатки принтеров будут выставляться в Лувре, в Эрмитаже или на худой конец продаваться на художественных аукционах. Последнее вряд ли случится. На аукционах могут продать дискету, принадлежавшую компьютерному художнику (фетиш – сейчас так продаются гитары великих музыкантов). Дело в том, что у computer art нет понятия оригинала и копии[8]. А это может убить даже настоящие шедевры, которые иногда публикуются на обложках и внутри глянцевых изданий. Пушкин говорил: «Пóшло то, что пошлó в народ». Только самые гениальные произведения искусства способны выдержать такое испытание хождением в народ. Они-то и формируют пласт культуры, на котором базируется современная цивилизация.

Лучший способ охарактеризовать какое-либо явление – тем более в книге с претензией на искусствоведение –  это привести классическую цитату. Вот она:

Они сначала нравилися мне

Глазами синими, да белизною,

Да скромностью – а пуще новизною;

Да, слава богу, скоро догадался –

Увидел я, что с ними грех и знаться –

В них жизни нет, все куклы восковые;

А наши!...

Угадайте, о чем говорил пушкинский Дон Жуан! Да-да – и о компьютерной анимации, о рисунках, созданных с помощью компьютерной графики... Скажем мягче (и с надеждой) – о современных образцах этого симбиоза науки, технологии и искусства. Ведь, в компьютерных рисунках больше чувствуется несовершенный инструмент (новизна – парадокс high technology), чем художник.

Задача о пожарных ведрах: перебор

В решении задачи о пожарных ведрах на рис. 3.9 в пунктах 1 (одноведерная задача) и пункт 2 (двухведерная задача) формируются векторы a, V и V2 по 361 элементу в каждом[9]. Ключевой оператор решения использует встроенную функцию max, возвращающую максимальное значение своего аргумента – вектора (матрицы). Функции, возвращающей номер максимального элемента вектора (матрицы), в среде Mathcad нет – с рассуждениями по этому поводу читатель может ознакомиться в этюде 4. Поэтому на рис. 3.9 (как и на рис. 3.6 и 3.7) задействован оператор суммы, перебирающий все варианты ведер и запоминающий угол вырезки для изготовления одного ведра максимального объема – 66 градусов (пункт 1) или двух ведер с максимальным суммарным объемом – 117 и 243 (360-117) градусов (пункт 2). Наш метод перебора опасен тем, что если у вектора (матрицы) два и более максимальных значений (как у вектора V2), то в лучшем случае появится сообщение об ошибке, а в худшем – неправильный ответ (см. пункт 2 на рис. 3.9 с aопт[10]=360). При решении трехведерной задачи (пункт 3) на область максимума была как бы наброшена сетка, в узлах которой просчитаны значения «трехведерной» функции. Далее были определены координаты сетки, где данная функция максимальна. Такой контрольный расчет перебором еще раз показал, что третье ведро лишнее – мы получили уточненное решение двухведерной задачи из пункта 2.
Наше решение выглядит несколько извращенным – в функцию max, составляющую ядро расчета на рис. 3.9, и в другие, ей подобные, также заложен перебор: что-то другое здесь вряд ли придумаешь.
Хотя как сказать. Представим такую житейскую ситуацию. Садовод собрал на своем дачном участке урожай яблок и решил похвастаться самым крупном
плодом перед соседями. Будет ли он перебирать все яблоки, чтобы выбрать предмет гордости? Конечно, нет. Самое большое яблоко никому не нужно. Нас интересует самое большое яблоко с определенной степенью вероятности. Кроме того, в термин «большое» мы вкладываем не вес яблока и не его геометрические размеры, а его зрительный образ.

Пусть у нас 100 плодов. Берем первое попавшееся более-менее крупное яблоко и считаем, что оно самое большое со степенью вероятности, намного превышающей 1% (1/100). Второе выбранное яблоко (а оно, естественно, должно быть больше первого) существенно повышает вероятность выбора самого большого. Так очень скоро, перебрав (взвесив, измерив или просто оценив на глаз) всего лишь несколько яблок, а не все сто, можно выбрать относительно самое большое яблоко. Кто-то возразит, что яблоки перед отбором могут быть кем-то
отсортированы так, что самое большое окажется в хвосте очереди (на дне корзины). Но это уже будет искусственная ситуация, враждебная человеку[11]. Мы же говорим о дружественных
ситуациях. Данный алгоритм станет совсем естественным, если отбирается не самое большое, а, например, самое красивое яблоко. Здесь полный перебор будет уж совсем диким. К понятиям большое и красивое можно приложить теорию нечетких множеств, о которой речь пойдет в этюде 6.
К сожалению, задачи, приведенные в данной книге, начиная с самой простой (задача о купце и сукне – см. этюд 1) и заканчивая самой сложной (это, наверное, задача о трехсторонней дуэли – см. этюд 6), нельзя отнести к разряду естественных. Все они довольно надуманные, призванные скорее иллюстрировать возможности Mathcad, а не показывать пути решения практических задач. Автора утешает и одновременно огорчает то, что таким недостатком грешат почти все книги по программным средам. Надуманная задача – это призма, сквозь которую вдумчивый читатель посмотрит на реальную задачу.

Ввод и сортировка двух векторов

В пункте 1 на рис. 4.1 переменным X и Y присваиваются транспонированные векторы-строки, а не просто векторы-столбцы. Это делается для компактности записи. Кроме того, элементы векторов имеют лишние нули – 4.0 вместо 4 и т.д. За счет этого выравниваются по вертикали пары значений Xi и Yi. Без такой маленькой хитрости рано или поздно пары собьются, что будет мешать их просмотру и редактированию. Альтернативное решение этой проблемы – хранение пар данных в матрице с двумя строками и с числом столбцов, равным числу пар[1].
Считается, что программиста от простого смертного можно отличить по простому тесту. Если программиста поставить в голову шеренги и приказать: «По порядку рассчитайсь!», то программист сначала уточнит, по какой системе нужно рассчитываться (двоичная, восьмеричная, шестнадцатеричная, десятеричная[2]...), а потом выкрикнет: «Нулевой!» В среде Mathcad по умолчанию номер первого элемента вектора (первого ряда и первого столбца матрицы) нулевой. Именно поэтому при семи экспериментальных точках, координаты которых заносятся в векторы X и Y, константа N равна шести (феномен программиста в строю). Номер первого элемента массивов и векторов хранится в системной переменной ORIGIN (an origin – начало, источник), значение которой (по умолчанию оно нулевое) в Mathcad-документе можно изменять (ORIGIN:=1, например). Допустимо менять и второе умолчание «шеренги» – систему счислений.
Ввести в среде Mathcad переменную-вектор можно двумя различными способами (см. этюд 1): отдачей команды Matrices из меню Math (Insert – Mathcad 7 и 8) либо нажатием на панели математических инструментов кнопки с изображением матрицы (щелкнув по ней курсором мыши) – см. рис. 1.7. Ввод за переменной ее индекса также допустим двумя способами: нажатием на панели математических инструментов на кнопку-иероглиф «Переменная с индексом» или набором за именем переменной символа открывающихся квадратных скобок (рудимент языков Pascal и C, где квадратные скобки означают индексную переменную).
Векторы X и Y совсем не обязательно вводить в Mathcad-документ вручную с клавиатуры. Если экспериментальный стенд оборудован средствами АСНИ (автоматизированной системой научных исследований) и данные с приборов заносятся на магнитный диск, то Mathcad-выражение X:=READPRN(имя файла) поможет считать их и оформить в виде Mathcad-вектора (матрицы) с именем X[3]. Кроме того, не следует забывать, что Mathcad – это полноценное Windows-приложение со встроенными средствами обмена в статике и динамике (Clipboard, DDE, OLE). Объемную задачу можно решить лишь тогда, когда голос Mathcad звучит в стройном хоре других приложений (графические, текстовые и табличные процессоры, базы данных, языки программирования и т.д.).

Двухмерная сплайн-интерполяция[11]

Далее автор приводит несколько пронумерованных «Советов тем, кто работает с Mathcad», которые публикуются в журнале КомпьютерПресс – на бумаге и на прилагаемом к журналу лазерном диске.
Педагогический опыт автора[12]
говорит о том, что студенты, выполняющие термодинамические расчеты, очень часто ошибаются в размерностях: складывают, например, джоули с британской единицей теплоты, а ответ записывают в калориях, забывая о соответствующем пересчете. Мы этой темы уже подробно коснулись в этюде 1. Среда Mathcad позволяет правильно (с соответствующими пересчетами) оперировать размерными величинами и «ругается» только в крайних случаях, когда, например, складывается длина с массой. Наша пользовательская функция hss(T, P) возвращает размерную величину (удельная энтальпия перегретого водяного пара), а ее аргументы (давление и температура пара) – также размерные величины.

Примеры работы двухмерной сплайн-интерполяции

На рис. 4.13 приведен пример формирования с помощью одномерной сплайн-интерполяции еще одной важной термодинамической функции одного аргумента – зависимости удельного объема кипящей воды от ее температуры.

Пример одномерной сплайн-интерполяции

Сплайн-интерполяция особенно критична на границах отрезка (области) существования аргументов. Вне этих границ речь идет уже не об интерполяции, а об экстраполяции – о предсказании значений функции за границами отрезка.
На рис. 4.14 показана работа функции predict, с помощью которой предсказывается
поведение какой-либо зависимости.

Экстраполяция

У функции predict (prediction – предсказание) три аргумента: вектор имеющихся данных (у нас 100 значений функции y(x) на интервале от 0 до 99 с шагом 1), число последних данных, учитываемых в предсказании (у нас их 50) и число предсказываемых данных (100). На графике на рис. 4.14 толстая кривая – функция y(x) на интервале 0-99, тонкая кривая – функция y(x) на интервале 100-199, а квадратики – предсказанные значения (не все, а только кратные 5), которые где-то в районе 160-170 обрываются.
Задание читателю, подготавливающее его к чтению следующего этюда, где будет описана математическая модель одной финансовой операции, – предсказать курс доллара на будущую неделю, опираясь на данные предыдущего месяца или года.
На рис. 4.15 проиллюстрирована работа сглаживающей функции supsmooth. Решается такая задача – сгладить функцию стоимости, например, комплектующих компьютера (см. задачу на рис. 6.33-6-35) в зависимости от объема закупки (скидка оптовикам).

Оценка качеств менеджера (начало)

В пункте 1 на рис. 4.16 оценки экспертов введены в матрицу M, содержащую девять строк (число экспертов n, j=1..9) и десять столбцов (число качеств m, i=1..10).
Пятибалльная средневзвешенная оценка деловых качеств менеджера определяется по формуле:
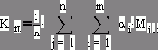                                                      (4.1)
где m – количество оцениваемых качеств, i := 1, 2.. m,
n – число экспертов, j := 1, 2.. n,
Мj,i – оценка j-м экспертом i-го качества в баллах,
ai – весовой коэффициент для i-го качества.
Весовые коэффициенты определяют относительную значимость качеств: если i-е качество представляется незначимым, то весовой коэффициент ai равен нулю. Придание коэффициенту
ai значения, равного единице, делает незначимыми все остальные качества. Весовые коэффициенты должны удовлетворять следующему условию:
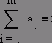                                                                             (4.2)
Значения весовых коэффициентов могут быть установлены различными способами:

лицом, принимающим решения (ЛПР);

экспертом с соблюдением условия (4.2);

по результатам экспертных оценок качества, косвенно отражающих мнения экспертов о значимости оцениваемых характеристик.

В последнем случае весовые коэффициенты рассчитываются по формуле:
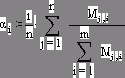                                              (4.3)
Вычисленные значения весовых коэффициентов в табличной и графической формах представлены в пункте 3 на рис. 4.17.

Оценка качеств менеджера (окончание)

Средневзвешенная оценка качества менеджера в баллах (пункт 4 на рис. 4.17) ¾ Kм = 4.162.
Алгоритм определения весовых коэффициентов ai влияет на оценку качества, которая может быть выполнена по выбору ЛПР на основе гипотезы равной значимости весовых коэффициентов:

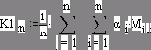
где ai = 1 / n.
В этом случае оценка качества значительно возрастает (в сравнении со средневзвешенной оценкой) – K1м
= 4.593.
Значения весовых коэффициентов могут быть установлены с учетом специфики конкретного заказа из условия приоритета  качеств (требуется «высокий» профессионал, личность приятная во всех отношениях, но без особой склонности к руководству). В этом случае приоритеты могут быть установлены, например, на следующих значениях: для профессиональных качеств ¾ kп1=1.15, личностных ¾ kп2 =1.05, деловых ¾ kп3 =0.8. Значения весовых коэффициентов для групп качеств r определяются формулой:
(ar)i = kпr / n,     где  n = 9,  r= 1, 2, 3,
и равны – (a1)i =
1.15 / 9 = 0.128; (a2)i =  1.05 / 9 = 0.117; (a3)i =  0.8 / 9 = 0.089.
Вектор-строка весовых коэффициентов имеет вид:

i		1		2		3		4		5		6		7		8		9
(ar)I		(a1)i		(a1)i		(a1)i		(a2)i		(a2)i		(a2)i		(a3)i		(a3)i		(a3)i

Средневзвешенная оценка качества менеджера  в баллах (пункт 8 на рис. 4.17) ¾
Kм
= 4.496.
Итак, в рассмотренном примере в зависимости от способа определения весовых коэффициентов получены три оценки качества:
Km = 4.162 – при экспертной оценке a;
K1m
= 4.593 – случай равнозначимых весовых коэффициентов;
K2m = 4.496 – при приоритете (kп1=1.15) профессиональных качеств.
Выбор кандидата – прерогатива лица, принимающего решение, или конкурсной комиссии.
Рассмотренная методика применима для оценки качества продукции, результатов испытаний, экзаменов и других задач экспертной оценки.
Возможно, руководителю группы экспертов или заказчику экспертизы потребуется анализ результатов работы экспертов для оценки их компетентности, пристрастий или добросовестности.

Весовые коэффициенты i-го качества в оценке j-го эксперта рассчитываются по формуле



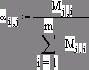
Результаты расчета содержатся в матрице a (пункт 5 на рис. 4.17).

Для наглядного представления результатов работы экспертов, анализа оценок, близости объекта к эталону качества в некоторых задачах очень удобна радарная диаграмма (Radar-diagram). Пример – экспертиза проекта электростанции по таким показателям: экономичность, экологичность, архитектурные решения, совместимость с еще не подпорченным ландшафтом, безопасность, надежность, значимость для экономики региона и др. Для всех показателей из центра диаграммы проводятся лучи, на которых откладываются средние значения оценок экспертов. Соединив точки на лучах, получим многоугольник. Эталону качества будет соответствовать вписанный в окружность с радиусом М (М – высший балл по шкале оценок) правильный многоугольник[17]. Степень приближения к эталону наглядно представляется формой и относительной площадью получившегося на основе оценок экспертов многоугольника (пункт 2 на рис. 4.6).

Тема оценки качества далеко не исчерпана. Интересные решения могут быть получены с использованием теории нечетких множеств (см. этюд 6).

[1] Сравните пары римских и арабских чисел на рис. 6.47.

[2] В среде Mathcad при форматировании чисел допустимо менять систему счислений. Двоичная система появилась только в Mathcad 8.

[3] Для поддержки АСНИ существуют также и специализированные программные средства – LabVIEW, LabWindows (разработка National Instruments, Corp.), например.

[4] Здесь лучше записать не нуль, а системную (предопределенную) переменную ORIGIN. Так мы и поступим в пункте 3.2 на рис. 4.2.

[5] Здесь чаще используют термин «аппроксимация» – приближение прямой линии к точкам. Еще здесь упоминают регрессию

– зависимость средней величины (прямая линия) от других величин (экспериментальные точки). Тут можно усмотреть некую путаницу в терминологии. Надеемся, что читатель в данном случае сам разберется, что к чему.

[6] Третья группа инструментов решения задач – это команды меню.


[7] Градация на линейную и нелинейную аппроксимацию весьма условна.

[8] Вот здесь-то и пригодятся средства символьной математики (этюд 7).

[9] На него нужно предварительно поместить курсор.

[10] Студенты автора называют ее «тормозная бабушка».

[11] Операторы функции, формируемых на рис. 4.10 и 4.13, объединены в единый операторный блок. Это позволяет использовать механизм локальных переменных – см. этюд 6.

[12] Автор советов – преподаватель Московского энергетического института. Основа не только российской, но и мировой энергетики – это теплоэнергетика (ТЭС и АЭС), где рабочее тело – в основном, вода и водяной пар.

[13] Если создаваемая функция будет использоваться для решения обратной задачи (поиск, например, значения температуры при заданных значениях давления и энтальпии пара), то такие сообщения об ошибке лучше убрать. При численном поиске корня уравнения (а к этому сводится такая задача) ничего не будет страшного в том, что мы временно будем вылезать из области разумного существования аргументов.

[14] Главка написана совместно с М.Панько.

[15] Понятие «эталон качества»- синоним оценки «высочайшее качество».

[16] Существенный недостаток данной методики в том, что все эксперты обязаны оценить все без исключения качества испытуемого. Мы должны заполнить прямоугольную таблицу – матрицу. Но в реальной жизни далеко не все привлеченные к этой работе являются признанными экспертами в оценке всех качеств объекта исследования. Мы уже сталкивались с подобной проблемой, втискивая табличные данные по энтальпии пара в квадратную матрицу – см. рис. 4.10.

[17] Вспомним чеховское: «В человеке все должно быть прекрасно – и лицо, и одежда, и душа, и мысли!»

Линейное сглаживание

Задача аппроксимации, и не только линейной – это типичная оптимизационная задача (см. этюды 2 и 3 и линии уровня в пункте 3.2 на рис. 4.2), сводящаяся к поиску минимума целевой функции СКО (среднеквадратичное отклонение) двух переменных a и b. В свою очередь, линейное сглаживание сводится к решению системы линейных алгебраических уравнений (см. этюд 1 и пункт 3.3 на рис. 4.2), состоящей из приравненных к нулю частных производных функции СКО по коэффициентам a и b.
Решение, показанное в пункте 3.2, предпочтительней для сферы образования – оно как бы «кричит» о сути метода наименьших квадратов: в функции СКО фигурирует квадрат, а сама функция минимизируется.

Определение точки с максимальным отклонением от прямой

Найденные тем или иным способом значения коэффициентов a и b сглаживающей функции y(x) = a + b×  x позволяют построить на графике прямую с роящимися вокруг нее точками (у нас квадратиками – рис. 4.3). Подобным графиком на практике, как правило, завершают обработку экспериментальных данных: график, во-первых, даст наглядное представление о качестве сглаживания, а во-вторых, поможет в случае чего отловить допущенные ошибки ввода исходных данных (пропуск десятичной точки, например). Этой цели может служить и предварительная сортировка векторов (см. пункт 2 на рис. 4.1): ошибочные значения (промах эксперимента, неправильный ввод данных) часто всплывают на концах упорядоченного вектора. В-третьих, график сам по себе ценен. С помощью графика, то есть с другого конца, можно довольно быстро решить задачу линейного сглаживания. У автора в лаборатории есть сотрудница, у которой глаз-алмаз: она при помощи тонкой прозрачной линейки так проводит прямую вблизи экспериментальных точек, что по ней можно определить коэффициенты a и b с точностью не меньше трех процентов (толщина карандашной линии).
Несколько слов о графических возможностях Mathcad и других подобных пакетов. Если студент начнет строить график функции по технологии, заложенной в математическом пакете, то автор выгонит такого студента с занятий, да притом вослед будет улюлюкать и топать ногами. Все (скажем осторожнее – почти все) математические пакеты при построении графиков никак (почти никак) не используют элементы искусственного интеллекта, а просто сканируют значение аргумента и проставляют точки с заданным пользователем шагом или с шагом, определяемым разрешением дисплея (принтера). Студентов же учат совсем другому – анализу функции, поиску характерных точек (корней, минимумов, максимумов, точек перегиба и т.д.), опираясь на которые и строится график: парабола, гипербола или какая-нибудь там лемниската Бернулли (см. рис. 1.18 в этюде 1). Но Богу – Богово, кесарю – кесарево, машине – машиново. Беда многих преподавателей в том, что они относятся к математическим пакетам не как к инструментальным средствам, требующим определенной сноровки и навыка (и головы, конечно), а как к своим своеобразным коллегам, которых на пушечный выстрел нельзя подпускать к студентам, изучающим математику, дабы они (студенты) не набрались от них (от пакетов) разных глупостей. Дежурная фраза одной знакомой автора: «Mathcad – круглый дурак, Maple – полный кретин, Mathematica – законченная идиотка».

Нелишне дополнить результаты сглаживания указанием точки, максимально отклонившейся от прямой (см. рис. 4.3). Само значение такого выброса найти несложно через функцию max. А вот с определением координат этой точки придется повозиться: привлечь аппарат булевых выражений, принимающих два значения – True (в среде Mathcad – единица) и False (нуль), умножение которых на текущий индекс фиксирует искомую координату.

В пакете Mathcad более 50 встроенных операторов (см. приложение 2) и почти 300 функций (см. приложение 3). Пять встроенных функций (csort, intercept, slope, min и max) были задействованы в задачах на рис. 4.1-4.3. Когда программисту предстоит решать какую-либо локальную задачу, то перед ним часто встает альтернатива: кодировать ли решение прямо в программе или выносить его наружу, оформляя в виде процедуры (функции). Считается, что глупый человек учится на своих ошибках, а умный – на чужих. Начинающий программист пишет свои процедуры (функции), а опытный ищет их в наборе ранее созданных. Знание пакета Mathcad – это на 90% знание операторов и функций[6], в него встроенных. Остальное – ловкость рук и программирование (средство создания новых инструментов – см. этюд 6).

Есть три причины, заставляющие даже сверхумного программиста отказываться от готовых программных форм и «изобретать велосипед». Первая причина лежит в сфере образования: тексты программ должны быть прозрачными для обучаемых. Во-вторых, в открытый участок программы легко ввести дополнения и изменения, расширяющие сферу ее применения и/или снимающие ранее наложенные ограничения. Так устроен, к примеру, пакет MatLab (разработка фирмы The Math Works). В его состав входят исходные тексты на языке C всех встроенных процедур и функций, так что пользователь перед включением их в работу может что-то узнать о методах, заложенных в них, и/или прощупать их работоспособность. В-третьих, всегда есть опасения, что в готовую программную форму затесалась чужая ошибка, которая, как бомба замедленного действия, может взорвать всю программу в самый неподходящий момент – после сдачи готового программного продукта заказчику или после того, как он разойдется по дилерской сети. Пример у нас под рукой (рис. 4.3). При всем богатстве встроенных функций пакету Mathcad не хватает функции определения в векторе или в матрице координат минимального (максимального) элемента. Выход из положения – это сумма (для вектора) или двойная сумма (для матрицы) произведений номера текущего элемента на булево выражение (см. рис. 4.3). Эту конструкцию так и хочется оформить в виде новой функции с именем imax, например, и больше с такой задачей не возиться. Но в новую функцию перекочует и будет замаскирована ошибка – неясно, что будет возвращать новорожденная функция imax, если в аргументе-векторе (в массиве) два или более максимальных элементов. Из прозрачной формулы с суммой это понятно, а из «затененной» функции imax – нет. Все эти замечания можно отнести и к встроенным функциям intercept и slope, возвращающим значения коэффициентов сглаживающей прямой. Всегда остаются сомнения, а нет ли в этих функциях фактической или методологической ошибки. Последнюю можно обнаружить, если подставить в функции intercept и slope аргументы-векторы с двумя или даже одним элементом. Через две точки всегда можно провести прямую. Через одну точку прямых можно провести бесчисленное множество. И в том, и в другом случае сумма квадратов отклонений двух точек (одной точки) от прямой будет минимальной (нулевой), и требования метода наименьших квадратов будут выполняться абсолютно. Но в первом случае функции intercept и slope будут решать простую интерполяционную задачу, для которой в среде Mathcad есть особый математический аппарат (см. ниже). Во втором случае (X и Y – не векторы, а скаляры) функции intercept и slope должны выдавать бесчисленное множество значений, связанных ограничением Y = a + b × X. В плане выполнимости критерия наименьших квадратов здесь все безупречно, но методология, заложенная в функции intercept и slope, приводит к тому, что при числе элементов в векторах X и Y, меньшем двух, выдается сообщение об ошибке. Но все это слабая защита, которую пользователь легко может обойти, подсунув функциям intercept и slope более одной точки, но с повторяющимися значениями аргументов. Резюме: играть можно не только с игровыми программами. На эту роль подходят и серьезные математические пакеты – было бы желание у пользователя. Компьютер же, как здоровая молодая собака, всегда готов играть со своим хозяином. Замахнется, к примеру, человек палкой, но не бросит ее, – собака прыгает, вертит головой, но не знает, куда бежать. Подсунет пользователь машине хитрый аргумент – функция не знает, что с ней делать, и выдает какие-то странные сообщения об ошибках, веселящие пользователя.

Есть направление в искусстве под названием поп-арт – популярное искусство. Методика обработки статистических данных, показанная на рис. 4.2, может быть названа поп-статом.

Аппроксимация полиномом 3-й степени

На рис. 4.4 формируются матрица A коэффициентов при неизвестных и вектор B свободных членов системы четырех линейных алгебраических уравнений, к которой сводится задача об аппроксимирующем полиноме третьей степени (кубическом). Сама система может решаться либо матричными операторами (a:=A-1×B), либо обращением к встроенной функции lsolve (см. пункт 3.3.2 рис. 4.2). Полноценный программный пакет всегда должен предоставлять пользователю возможность сделать какую-либо операцию двумя, а еще лучше тремя различными способами. Пользователь будет чувствовать себя комфортно в программной среде, если его право выбора не ограничено. На выбор же могут влиять не только сомнения в качестве тех или иных готовых инструментальных средств (см. выше) или нечеткое знание области их применения, но и вкусовые предпочтения пользователя. Решение системы линейных алгебраических уравнений (базовая задача любого Решателя) через матричные операторы неудобно тем, что пользователь все время напарывается на сообщения об ошибках, набирая R:= B / A или R := B × A-1. Крамольность первого выражения очевидна – в математике нет понятия матричного деления. Но почему нельзя писать R := B × A-1, знают далеко не все. Так или иначе, о KISS-принципе не следует забывать. Помнить следует и другое предостережение, зафиксированное в пословице: «Простота хуже воровства». Выкладки рис. 4.4, от которых рябит в глазах из-за обилия «сигм», можно упростить вводом переменных с индексом Ak,m и Bk (рис. 4.9). Но! Автор уже раз обжегся на суммировании в среде Mathcad, когда рассматривал систему искусственного интеллекта SmartMath (рис. 7.15 в этюде 7): за суммой, особенно тройной с пересекающимися индексами, может таиться ошибка.

Сглаживание с использованием функции linfit

Аргументы функции linfit – числовые векторы X и Y и вектор-функция f, хранящая набор пользовательских сомножителей (на рис. 4.5 – это 1, 1/x, 1/x2 и 1/x3), коэффициенты которых функция linfit возвращает в вектор a, опираясь на метод наименьших квадратов (см. рис. 4.5).

Нелинейное сглаживание

1. В среде Mathcad есть функция genfit (GENeral FITting – общее сглаживание), допускающая множество параметрических коэффициентов у сомножителей произвольного вида. Она, в отличие от функции linfit, решает нелинейную[7]
задачу аппроксимации. Пример использования функции genfit дан в пункте 7.1 на рис. 4.6. В функцию-вектор f необходимо занести не только само сглаживающее выражение (у нас это экспоненциальная функция), но и его частные производные[8] по искомым параметрам a0 и a1,.объединенным в вектор. Из-за того, что нелинейная задача может иметь более одного решения, функция genfit требует начального приближения (третий аргумент-вектор), вблизи которого и ищется одно из решений.
2. Без функции genfit задачу нелинейной аппроксимации, как правило, решают линеаризацией
исходных данных, подключая к работе уже известные нам функции intercept и slope. В нашем случае (пункт 7.2 на рис. 4.6) при исходном уравнении Y=a × x b  встроенные функции intercept и slope прикладывают к новому уравнению Ln(Y)=Ln(a)+b×Ln(X). Но это приводит к некоторому искажению математической модели: сумма X и сумма логарифмов X – это далеко не одно и то же.
3. В ряде случаев при решении задачи нелинейной аппроксимации можно обойтись и без функции genfit (пункт 7.1 рис. 4.6), и без искажающей линеаризации (пункт 7.2), применив открытый алгоритм поиска значений коэффициентов a0 и a1, минимизирующих целевую функцию – сумму квадратов отклонений точек от кривой. Расчет, показанный в пункте 7.3 на рис. 4.6, кроме того, не требует знания частных производных сглаживающего уравнения.
В конце рис. 4.6 приведено графическое сравнение трех методов нелинейного сглаживания. Из графика видно, что линеаризация исходных данных (пункт 7.2) привела к существенным искажениям результата. Поиски же параметрических коэффициентов через функцию genfit (пункт 7.1) и через минимизацию (пункт 7.3) близки по результатам.
Практический совет по выбору наиболее подходящей формулы для сглаживания. В Mathcad-документе можно хранить набор формул, подключая одну из них по мере надобности к статистической обработке экспериментальных точек. В диалоговом окне Properties (свойства – оно вызывается командой Properties в меню Format) есть переключатель Disable Evaluation (Запретить вычисления), позволяющий превращать математические выражения[9]
в комментарий:

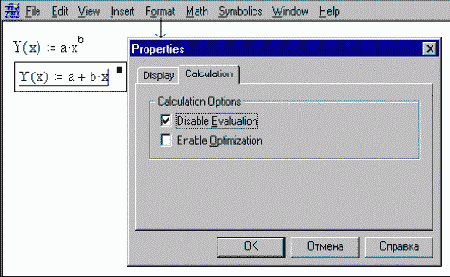
Данный переключатель превращает выражение в комментарий (что отмечено черным квадратиком правее выражения) и переопределяет тем самым функцию пользователя. О втором переключателе (Enable Optimization – Разрешить оптимизацию) будет рассказано в этюде 7 (раздел 7.3).
В Mathcad-документе можно записать множество функций пользователя, подключая одну из них к аппроксимации: линейной (рис. 4.2), экспоненциальной (рис. 4.6), логарифмической и т.д., и подбирая тем самым наилучшую модель обработки экспериментальных данных. Выбор формулы можно вести и без переключателя Disable Evaluation, опираясь на свойство среды Mathcad включать в расчеты только последнюю запись функции. Нужную функцию можно просто перетаскивать (технология drag-and-drop) в конец списка.

Интерполяция сплайном

Отличия в линейной (lspline), параболической (pspline) и кубической (cspline) интерполяции сплайном заметно проявляются только на концах отрезка X1-XN. Эти области на рис. 4.8 рассмотрены «под лупой». Здесь нужно говорить уже не об интерполяции, а об экстраполяции (см. ниже рис. 4.14)
Несложно через точки провести полином N-й степени (рис. 4.9):

Интерполяция полиномом

Но нанизать опытные точки на интерполяционный «шампур», напрочь игнорируя неизбежные ошибки эксперимента, может только совсем безграмотный исследователь. У интерполяции другие сферы применения. Расскажем об одной из них. При решении в среде Mathcad какой-либо задачи нередко образуется составная функция[10], обращение к которой вызывает длинную цепочку сложных вычислений, связанных с поиском корней уравнения, с дифференцированием, интегрированием и т.д. Работать с такой функцией становится невмоготу даже на мощном компьютере. Один из выходов – омолаживание «бабушки»: табулирование «тормозной» функции с последующей заменой ее на эрзац-функцию, опирающуюся на интерполяцию – линейную, нелинейную или сплайном. И что удивительно, «омоложенная» функция, хоть и теряет напрочь свою физику, но в особых условиях может возвращать более точное значение, чем ее прародительница, в которой накапливаются ошибки численных методов. Узлы же интерполяции можно просчитать на пределе точности.

Задача об эпидемии – разностная схема

Все это словесное описание модели эпидемии легко вмещается в Mathcad-документ (рис. 5.1) с двумя формулами (пункт 2), объединенными в вектор, что эквивалентно BASIC-конструкции:
For t = 1 To 13
            Больные(t + 1) = Пр * Больные(t) * Здоровые(t)
            Здоровые(t + 1) = Здоровые(t) - Больные(t)
Next
Если бы два выражения в пункте 2 на рис. 5.1 не были заключены в скобки, то их выполнение сразу бы прерывалось сообщением об ошибке. Система Mathcad пыталась бы сначала полностью заполнить вектор Больные, а уже потом – вектор Здоровые. Скобки изменяют порядок счета: он ведется не по строкам, а по столбцам: сначала заполняются вторые элементы векторов Больные и Здоровые (первые элементы заполняются в пункте 1 – начальные условия), а потом третьи и т.д. Этими скобками мы меняем естественный порядок выполнения операторов[1]
¾ они выполняются не слева направо и не сверху вниз, а крест накрест.
Результаты расчета графически отображены[2]
в пункте 3. На тринадцатый день (спад эпидемии) в городе было 105 больных. Критическая точка – девятый день (3972 больных), ради поиска которой и затевают весь этот расчетный сыр-бор: моделируя эпидемию, мы можем распланировать работу санитарных служб города – подвезти в аптеки лекарства, отозвать врачей из отпуска, выписать из больниц выздоравливающих и т.д. В оригинальном решении задачи дополнительно прослеживается динамика изменения числа умерших во время эпидемии. Но мы исключим эту печальную кривую. Тем более что она и математически не вписывается в задачу: динамика числа умерших просчитывается отдельно от динамики больных и здоровых.

Задача об эпидемии – решение системы дифференциальных уравнений

В пункте 5 рис. 5.2 столбцы матрицы Z (время, число больных и число здоровых) разнесены по отдельным векторам и отображены графически, что позволяет проследить динамику развития эпидемии.
На рис. 5.2 получены несколько иные результаты, чем на рис. 5.1, хотя характер кривых сохранился: максимум больных (3119) наблюдается не на 9-й, а на 7-й день, на 13-й день мы имеем не 105, а 209 больных. Это объясняется и различными значениями точности расчетов (на рис. 5.1 делалось 13 шагов интегрирования, а на рис 5.2 ¾ 500) и различными примененными методиками (Эйлер против Рунге и Кутта[5]).
В функцию rkfixed заложен широко распространенный метод решения дифференциальных уравнений – метод Рунге ¾ Кутта[6]. Несмотря на то что это не самый быстрый метод, функция rkfixed почти всегда справляется с поставленной задачей. Однако есть случаи, когда лучше использовать более сложные методы. Эти случаи попадают под три широкие категории: система может быть жесткой[7]
(Stiffb, Stiffr), функции системы могут быть гладкими
(Bulstoer) или плавными (Rkadapt). Нередко приходится пробовать на одном дифференциальном уравнении (одной системе) несколько методов, чтобы определить, какой метод лучше (быстрее, точнее). Примерно так мы сравнивали в этюде 3 разные способы поиска оптимумов функции.
Когда известно, что решение гладкое, используется функция Bulstoer, куда заложен метод Булирша ¾ Штёра, а не Рунге ¾ Кутты, используемый функцией rkfixed. В этом случае решение будет точнее. Список аргументов и матрица, получаемая при работе с функцией Bulstoer, такие же, как и при работе с rkfixed.
Можно решить задачу более точно (более быстро), если уменьшать шаг (у нас это Dt) там, где производная меняется быстро, и увеличивать шаг там, где она ведет себя более спокойно. Для этого предусмотрена функция Rkadapt (adaption –адаптация). Но, несмотря на то что при решении дифференциального уравнения функция Rkadapt использует непостоянный шаг, она тем не менее представит ответ для точек, находящихся на одинаковом расстоянии, заданном пользователем. Аргументы и матрица, возвращаемая функцией Rkadapt, такие же, как при rkfixed.

При решении жестких систем следует использовать одну из двух встроенных функций, разработанных специально для таких случаев: Stiffb и Stiffr.
Они используют метод Булирша ¾ Штёра (b) или Розенброка (r). Форма матрицы-решения, полученной с помощью этих функций, идентична матрице, полученной через rkfixed. Однако Stiffb и Stiffr требуют дополнительного аргумента J:
Stiffb(x, tнач, tкон, n, f, J)
Stiffr(x, tнач, tкон, n, f, J),
где
x – вектор n начальных значений;
 tнач, tкон – конечные точки интервала, в котором должно быть найдено решение дифференциальных уравнений. Начальные значения x определяются в точке tнач;
n – количество точек за начальной точкой, в которых должно быть определено решение. Это определяет число рядов (1 + n) матрицы, которую генерируют функции Stiffb и Stiffr;
f(t, x) – функция-вектор правых частей системы;
J(t, x) – матрица-функция размерности n×(n+1), в которой содержится матрица Якоби правых частей дифференциальных уравнений.
В функциях для решения дифференциальных уравнений, описанных ранее, предполагалось, что необходимо получить таблицу значений x(t) относительно значений t, расположенных на одинаковом расстоянии друг от друга на отрезке интегрирования, ограниченном точками tнач и tкон. Но часто требуется найти решение только в конечной точке tкон. Хотя описанные функции определяют значение x(tкон), они проделывают при этом много ненужной работы, высчитывая промежуточные значения x(t).
Если необходимо узнать только значение x(tкон), используются следующие функции:
bulstoer( x, tнач, tкон, acc, f, kmax, save)
rkadapt( x, tнач, tкон, acc, f, kmax, save)
stiffb( x, tнач, tкон, acc, f, J, kmax, save)
stiffr ( x, tнач, tкон, acc, f, J, kmax, save),
где
x – см. выше;
tнач, tкон – конечные точки интервала, на котором должно быть найдено решение дифференциальных уравнений. Начальные значения t определяются в точке tнач;
acc – контролирует точность решения. При небольших значениях acc делаются более мелкие шаги вдоль траектории, что увеличивает точность решения;


f(t, x) – см. выше;
J(t, x) – см. выше;
kmax – максимальное количество промежуточных точек, в которых будет найдено решение. Значение kmax устанавливает верхнюю границу количества рядов матрицы, получаемой этими функциями;
save – наименьшее допустимое расстояние между величинами, в которых должно быть найдено решение. Значение save устанавливает нижнюю границу разницы между любыми двумя числами в первой колонке матрицы решения.
Вернемся к нашему примеру с эпидемией. Если известно начальное число больных (N=50 – см. пункт 1 на рис. 5.1), то это значит, что их сразу пересчитали. А если это так, то их знают поименно. Но в этом случае больные должны быть изолированы, и никакой эпидемии не будет вообще (Пр=0). В реальной задаче мы можем знать число жителей в городе (число здоровых на день начала эпидемии) и число больных в какой-то последующий день, когда становится ясно, что разразилась эпидемия. Другими словами, нам что-то известно о параметрах на краях отрезка, охватывающего некий динамический процесс.
На рис. 5.3. реализован метод последовательных приближений для решения по разностной схеме такой краевой задачи: в начале эпидемии в городе 20 000 здоровых жителей, а в конце эпидемии – 100 больных. Спрашивается, сколько больных было в начале эпидемии.

Решение краевой задачи об эпидемии разностной схемой

Ответ (51 больной) получен за семь приемов: задается начальное число больных, которое корректируется в зависимости от того, какое число больных оказывается в конце эпидемии. На рис. 5.3 можно, конечно, не дублировать Mathcad-оператры, а просто вручную подправлять первое приближение.
С помощью функций Bustoer, bustoer, Rkadapt, rkadapt, rkfixed, Stiffb, stiffb, Stiffr и stiffr, решающих задачу Коши, краевую задачу можно также решить последовательными приближениями (см. рис. 5.4 с функцией rkfixed):

Решение краевой задачи об эпидемии функцией rkfixed

Нижняя кривая на рис. 5.2 похожа на траекторию полета снаряда[8], поэтому метод последовательных приближений, приложенный к краевой задаче, называют также методом стрельбы: можно менять искомые начальные условия, последовательно приближаясь к решению, имея на другом конце отрезка «корректировщика огня», в лексиконе которого три слова: «перелет», «недолет» и «попал» («почти попал», учитывая заданную точность расчета – см. комментарии на рис. 5.3). По правде говоря, метод стрельбы берет свое название не от вида кривой, а от особенностей решения краевой задачи применительно к дифференциальному уравнению второго порядка, когда приходится менять угол наклона ствола пушки – значение первой производной на конце отрезка интегрирования. В нашей задаче об эпидемии (система двух обыкновенных дифференциальных уравнений) для попадания в цель приходится менять не угол наклона пушки, а ее подъем над землей – число больных в начале эпидемии. Тут, как правило, используют метод половинного деления, когда отрезок «перелет-недолет» делят пополам.

Решение краевой задачи об эпидемии функцией sbval

Метод стрельбы заложен и во встроенную функцию sbval, работа которой показана на рис. 5.5. Она требует начального приближения и соблюдения некоторых условностей, связанных с нашими знаниями состояний решаемой системы на концах отрезка интегрирования. Функция sbval не совсем обычная. Мы привыкли к тому, что, например, операторы A:=sin(X) и A:=sin(30) идентичны, если переменная X имеет значение 30, несмотря на то, что в первом случае у функции sin в качестве аргумента выступает переменная, а во втором – константа. Функция же sbval в этом отношении аномальна. Она возвращает значение в зависимости не только от конкретных значений аргументов, но и от того, введены они в виде переменных (x0) или в виде констант (20 000). Из-за этого даже специалистам по дифференциальным уравнениям часто приходится ломать голову, чтобы сообразить, как можно условия краевой задачи «запихнуть» в функцию sbval. Здесь фирма MathSoft несколько отошла от первоначальной идеологии пакета Mathcad, подразумевавшей, что запись условия задачи на экране дисплея должна выглядеть естественно.
Типичный пример – численное решение в среде Mathcad системы алгебраических уравнений: сначала задается начальное приближение к корню (ведь корней может быть много), потом за ключевым словом Given (дано) в естественном виде пишется сама система уравнений, после которой помещается функция Find, возвращающая значения своих аргументов, превращающих ранее записанные уравнения (до слова Given) в тождества. Функция Find также аномальна: она возвращает значения, зависящие не только от значений аргументов, но и от того, что вблизи нее находится. Это, конечно, грубейшее нарушение правил построения функциональных зависимостей. Но разработчикам Mathcad пришлось пойти на это ради того, чтобы алгебраические уравнения в Mathcad-документе хранились в естественной форме. При создании математических пакетов типа Mathcad приходится решать не только чисто математические проблемы (разработка алгоритмов решения и реализация их средствами вычислительной математики), но и проблемы единства формы представления задачи (интерфейс пользователя) и методов ее решения.

Функция sbval не решает краевую задачу, а только находит недостающие значения на краю отрезка. После этого краевая задача переходит в задачу с начальными условиями (задача Коши), которая и решается в пункте 7 рис. 5.5. Заодно проверяется точность решения: задали 100 больных – получим почти 100 (ошибка во втором знаке после запятой).
Для решения краевой задачи в среде Mathcad есть еще одна функция – bvalfit. Она используется в тех случаях, когда нет всей необходимой информации для функции sbval, но известно решение задачи в промежуточной точке. Функция bvalfit решает задачу с двумя граничными точками, начиная с конечных точек и следуя траекториям решения и его производным в промежуточных точках:
bvalfit( x1, x2, tнач, tкон, tf, f, load1, load2, score),
где
x1- вектор предполагаемых начальных значений, не определенных в точке х1;
x2 – то же для точки х2;
tнач, tкон – конечные точки интервала, в котором должно быть вычислено решение дифференциального уравнения;
tf – точка между tнач и tкон, в которой траектории решений, начатые с tнач, и траектории, начатые с tкон, должны совпадать;
f(t, x) – векторная функция, состоящая из n элементов, содержащая первые производные неизвестной функции;
load1(tнач, x1) – векторная функция, n элементов которой соответствуют значениям n неизвестных функций в точке х1. Некоторые из этих значений будут постоянными, заданными начальными условиями. Другие будут неизвестны вначале, но будут найдены. Если значение неизвестно, то следует использовать соответствующее предполагаемое значение из вектора x1;
load2(tкон, x2) – аналог load1, но для значений n неизвестных функций в точке х2;
score(tf, x) – векторная функция, состоящая из n элементов. Эта функция применяется для того, чтобы задать, как решения должны совпадать в точке tf. Обычно нужно определить score(tf, x):= x, чтобы все решения неизвестных функций совпадали в точке tf.
Функция bvalfit по своей сути решает две краевые задачи на двух смежных отрезках интегрирования. Она особенно полезна, когда производная имеет разрыв где-то внутри интервала интегрирования. При развитии эпидемии (наша задача) такое может произойти, если, например, комиссия из центра снимет с работы медицинское начальство города и тем самым изменит значение коэффициента Пр.
Второй тип задач с граничными условиями появляется при решении дифференциального уравнения с частными производными. В этом случае приходится фиксировать значение решения не в двух точках, как было сделано в предыдущей «плоской» задаче, а в совокупности точек, составляющих границу: в углах прямоугольника, например. В среде Mathcad имеются две функции (relax и multigird) для решения таких уравнений. Но разговор о них выходит за рамки этой книги. Скажем лишь то, что эти функции предназначены для решения дифференциальных уравнений конкретного вида – уравнений Лагранжа и Пуассона. Задачи другого вида требуют составления индивидуальной схемы решения с привлечением той же «плоской» функции rkfixed.

Моделирование развития финансовой пирамиды

В пункте 1 рис. 5.6 вышеприведенного протокола работы в среде Mathcad определяются константы – ее имя, знак присвоения (:=) и величина. Комментарии расшифровывают их.
В пункте 2 определяется состояние пирамиды на первый день: вводятся индексные переменные – первые значения векторов M, NK и MMM.
В пункте 3 записана динамика изменения курсов продажи и покупки акций – функции P(t) и K(t): объявляется о выпуске акций (билетов) номиналом в 100 рублей со следующим курсом продажи P и покупки K:
Таблица 5.1

Число дней, прошедших с начала эмиссии акций (билетов)		1		2		3		...		51		...		365		...
Продажа (руб.)		105		107		109		...		205		...		833		...
Покупка (руб.)		100		102		104		...		200		...		828		...

Из таблицы 5.1 видно, что купленная акция может дать дивиденд в 723% годовых при номинальной своей цене в 100 рублей. Если уровень инфляции достаточно высок, то люди верят в реальность таких огромных дивидендов и пирамида растет. Но опасность краха этой затеи ощущают почти все и отдают свои деньги не на год, а, допустим, на 50 дней (переменная Время – среднее время между покупкой и продажей акций – см. пункт 1). За этот период по каждой акции можно «наварить» магические 100 рублей, фигурирующие во многих пословицах и поговорках.
Далее векторы NK и NP заполняются по простой разностной схеме: известно предыдущее значение элемента вектора (на день t) – рассчитывается его очередное значение (на день t+1).
В городе, где строится пирамида, миллион жителей (N – см. пункт 1), среди которых царит некий ажиотаж, подогреваемый вышеприведенной таблицей курсов. Языком математики его можно описать формулой, связывающей число проданных населению акций в конкретный день (NK) с общим числом проданных акций (сумма NK за предыдущие дни) и условным числом жителей, не купивших пока акции (N минус сумма NK за предыдущие дни). Повторяем, развитие финансовой пирамиды во многом напоминает развитие эпидемии, когда число заболевших (купивших акции) в конкретный день пропорционально числу больных в городе (числу проданных акций), перемноженному на число еще не переболевших (не купивших акции). В случае эпидемии коэффициент пропорциональности зависит от мер профилактики. В случае финансовой пирамиды этот коэффициент (мы его условно назовем коэффициентом ажиотажа – KA) зависит от уровня инфляции, рекламы (вспомним Марину Сергеевну, Леню Голубкова и прочих «бабочек»), наличия других параллельных пирамид, от срока, прошедшего с момента шумного краха предыдущей пирамиды, и т.д. Многие экономические явления (кризисы, банкротства) прокатываются волнами. Период пика волн финансовых пирамид составляет, по различным оценкам, от 25 до 30 лет, что связано, во-первых, с приходом к активной жизни свежих, незатронутых пирамидами сил, и, во-вторых, с короткой людской памятью. На таких волнах многих ждет финансовое кораблекрушение. Другие же (а их намного меньше – и в этом фокус пирамид), подобно отважному и ловкому серфингисту, получают «финансовое» удовлетворение.
За волной купивших акции «катит» волна желающих их продать – вернуть свои «кровные» и причитающиеся дивиденды. Здесь мы также до предела упростим модель и будем считать, что волна продающих акции отстает от волны их купивших на число дней, хранящихся в переменной Время:
NPt+1 = 0, если t £ Время
NPt+1 = NKt-Время, если t > Время.
Волны покупателей и продавцов акций могут иметь разные формы – подчиняться, например, нормальному закону распределения (см. в этюде 6 рис. 6. 41 в этюде 6). Главное здесь раздвоенность волн: человек сначала покупает акцию (билет) и только потом ее продает.
Ну а теперь можно подсчитывать барыши и кататься на волнах финансовой пирамиды.

Развитие финансовой пирамиды

Несложно вычислить, сколько денег (вектор M ¾ см. пункт 5 на рис. 5.7) будет на счету организаторов пирамиды завтра (t + 1), если известно, сколько их в наличии сегодня (t), и если известен курс акций и количество покупок и продаж:
Mt+1 = Mt + NKt × K(t) - NPt × P(t)
Люди, покупающие акции, приносят деньги в кассу. Люди, акции сдающие, забирают деньги из кассы. Но есть еще один человек, залезающий в кассу. Это – организатор пирамиды, имеющий свой «профит», что выражается в том, что из кассы ежедневно изымаются три процента (Доход := 0.03 – см. пункт 1) наличных денег:
Доход × Mt
Естественно, доход изымается, если (if) в кассе есть деньги. В реальной жизни, конечно, касса худеет на значительно большие суммы – налоги, оплата текущих расходов, реклама и т.д. Расход := 300 000 – см. пункт 1.
В 1202 году Леонардо Пизанский (1180-1240) описал одну из первых моделей развития замкнутой биологической системы, населенной условными кроликами. Если соответствующим образом определить их плодовитость и долголетие, то численность популяции кроликов будет меняться из поколения в поколение по строгому закону:
Таблица 5.2

Поколение		1		2		3		4		5		6		7		...		27		...
Число кроликов		1		1		2		3		5		8		13		...		196 418		...

Читатель, конечно, уже догадался, что речь идет о числах Фибоначчи: Леонардо Пизанский более известен под именем Фибоначчи (Fibonacci – сокращение от filius Bonacci – сын Боначчи). В новом поколении кроликов их число будет равно сумме числа кроликов в двух предыдущих поколениях (см. программу на рис. 6.11 в этюде 6). Со временем про этих условных кроликов забыли, но числа Фибоначчи (1, 1, 2, 5, 8, 13 и т.д.) нашли применение в прикладной математике (см. этюд 6).
Наша модель развития пирамиды также позволяет сгенерировать некий числовой ряд, отображающий состояние дохода организаторов этой финансовой операции (вектор МММ):
Таблица 5.3

День		Доход (округлено до рублей)		Примечание
1		70 000 000		Начало пирамиды
2		72 100 000
3		74 128 022
4		76 086 206
...		...
168		303 058 831
169		303 485 168
170		303 635 916		День икс
171		303 635 916
272		303 635 916
...		...

<
/p> Назовем числа второго столбца таблицы 5.3 числами Мавроди[11]. Будем надеяться, что со временем о финансовых пирамидах забудут, но числа Мавроди войдут в историю. Тем более, что сам Сергей Мавроди по образованию математик.

В пунктах 5-6 графически отображено развитие пирамиды. Просматривая матрицу M, можно определить «день икс», когда прибыль организатора достигает максимума (у нас это 170-й день – см. пункт 7), и когда пирамиду пора разваливать – уходить на «дно», баллотироваться в депутаты или уезжать за границу. Благо денег на это «наварено» достаточно – почти триста миллионов при всего лишь трехпроцентной норме прибыли.

Мы же никуда пока не уезжаем, остаемся у своего компьютера и, собираясь вкладывать деньги в какое-то надежное или сомнительное предприятие, сначала должны просчитать, что из этого может выйти. Так мы легко можем вернуть и приумножить деньги, потраченные на приобретение компьютера и программы Mathcad[12], а также на операционные системы Windows, под управлением которой Mathcad работает.

Кроме того, читатель должен не забывать о задании, которое он получил, – решить задачу о финансовой пирамиде не по разностной схеме, а через дифференциальные уравнения.

[1] Об этом атрибуте программирования будет подробнее сказано в этюде 6.

[2] Здесь используются два типа декартова графика: линия с точками в виде квадратиков и так называемая bar-diagram – плоская столбчатая диаграмма.

[3] Или Ойлера – что в него заложено, можно увидеть в этюде 6 на рис. 6.3.

[4] Здесь лучше написать Тнач и Ткон, опустив индекс.

[5] Многие математики полагают, что есть только один метод Эйлера. Все остальное ¾ модификации этого метода.

[6] Или Рунге – Кутты, что в него заложено – см. рис. 6.3 в этюде 6.

[7] Термин «жесткий» происходит из механики, где численное решение некоторых систем дифференциальных уравнений требует разного шага интегрирования по разным искомым функциям.

[8] Она может быть совсем не похожа на траекторию полета снаряда, но… читаем дальше.

[9] В этюде 6 мы рассмотрим методику составления одной функции для такого рода расчетов, возвращающую сумму налога.

[10] Некоторые банки Великобритании предлагают своим клиентам такие условия: процент по вкладку равен уровню инфляции плюс 1-2%.

[11] Или числами ГКО, если вспомнить 17 августа 1998 г.

[12] См. в конце книги информацию о фирме СофтЛайн, официальном представителе MathSoft на российском рынке (рекламная пауза!).

Поиск корня алгебраического

Кроме «зашифрованности» алгоритма (чего стóят аргументы функции until на рис. 6.1) «беспрограммный» поиск корня имеет и другой недостаток: он приводит к нерациональному использованию ресурсов компьютера – к генерации векторов a и b, у которых нас интересуют только последние (last) элементы: между ними зажат искомый корень (переменная корень)[3].
Операторы if и until позволяют менять естественный порядок выполнения операторов в Mathcad-документе: сверху вниз и слева направо. Кроме того, есть еще два признака программирования: локальные переменные и объединение операторов в операторные блоки.
Путь 2. Версии Mathcad начиная с 4.0 – это полноценные Windows-приложения. При решении конкретной задачи в среде Mathcad можно в статике (через файлы на диске или через Буфер обмена – Clipboard) или в динамике (технология DDE и OLE) перенести данные (скаляр, вектор или матрицу) в среду, например, fortran’а и, используя богатый набор средств вычислительной математики этого языка, решить задачу (этап задачи). В среде Mathcad 7 Pro и 8 Pro эта технология была развита и визуализирована через инструментарий MathConnex (см. приложение 10).
Путь 3. Начиная с пятой версии Mathcad пользователям была предоставлена возможность программирования на языке С и объявления в среде Mathcad новых встроенных функций (операторов). Код этих функций нужно откомпилировать каким-либо 32-разрядным транслятором и прикрепить к среде Mathcad через механизм DLL. Но этот путь с самого начала был тупиковым. Во-первых, Mathcad создавался как инструмент решения широкого класса задач теми, кто не хотел или не умел возиться с классическими языками программирования. При обращении же к языку C получалось, что от чего ушли, к тому и пришли. Во-вторых, тот, кто все-таки переключался из среды Mathcad в среду языка С, как правило, там и оставался, решая всю задачу целиком. В-третьих (вернее, во-вторых с половиной), если кто-то и мог решить свою задачу на языке С, то он обычно не пользовался услугами Mathcad по моральным соображениям, считая это ниже своего достоинства. Но главным недостатком в технологии использования C для расширения возможностей Mathcad является невозможность включения в C-программу богатого математического инструментария Mathcad. Технология написания С-функций описана в приложении 8.

Расчет факториала (двусторонняя рекурсия)

Работая по программе с двусторонней рекурсией, показанной на рис. 6.10, можно не только правильно определить факториал нуля (единица), но и получить факториалы отрицательных (?!) чисел. Только нужно обучить этому машину – заложить в программу двустороннюю рекурсию для поиска факториала на всем целочисленном диапазоне[24]. «Двусторонность» здесь проявляется в том, что факториалы ищутся не только справа, но и слева от пяти.
Описывая в этюде 5 модель финансовой пирамиды, мы упомянули числа Фибоначчи, которые связаны с условными кроликами:

Поколение		...		4		5		6		7		8		9		10		11		...
Число кроликов		...		3		5		8		13		21		34		55		89		...

Приведенный ряд специально начат не с традиционного места (первое поколение), а с четвертого поколения (три кролика), для того чтобы задать читателю вопрос, подобный тому, который стоял в задаче о факториале: «Чему равно минимальное число кроликов в популяции – каково наименьшее число Фибоначчи?» Нормальный ответ, приводимый во всех учебниках, – ноль. Но не будем спешить и напишем программу с двусторонней рекурсией, взяв за базовые числа Фибоначчи не традиционную пару 0 и 1, а 13 и 21 (седьмое и восьмое поколения – см. рис. 6.11).

Расчет чисел Фибоначчи (двусторонняя рекурсия)

Ряд кроликов Фибоначчи в «отрицательных поколениях» зеркально отображает значения в «положительных поколениях», но с переменным знаком.
Числа Фибоначчи в наше время широко применяются в вычислительной математике, в том числе и для иллюстрации рекурсии, как, например, в нашей книге. Кроме того, метод Фибоначчи используется для поиска минимума. Частный случай метода Фибоначчи – метод золотого сечения (см. рис 6.26): пара смежных чисел Фибоначчи при N, стремящемся к бесконечности, соотносится по золотому сечению.

Расчет изящных чисел Фибоначчи (двусторонняя рекуррентность)

Использование рекурсии для поиска чисел Фибоначчи – это стрельба из пушки по воробьям. Намного эффективнее рассчитывать подобные числа в цикле, рекуррентно. На рис. 6.12 представлена программа, по которой ищутся, если так можно выразиться, изящные (fine) числа Фибоначчи[25], где базой будут тройка, семерка[26] и туз (11). Следующим изящным числом Фибоначчи будет 21 (3+7+11, тоже красиво – вспомним знаменитую карточную игру). Предыдущим числом окажется 1 (11-7-3, опять неплохо, если принять во внимание, что сестра таланта не только краткость, но и простота). Остальные изящные числа Фибоначчи, пользуясь программой на рис. 6.12, рассчитать несложно – главное тут суметь дать им «изящное» толкование.
В программе на рис. 6.12 еще раз подчеркнуто, что размещение нескольких операторов на одной строке – это недокументированный прием. Если такая «упакованная» программа будет давать неверный результат, то фирма MathSoft за это ответственности не несет. Мы же будем считать такую программу «заархивированной» и не занимающей много места в книге. Такую программу при вводе в компьютер требуется «разархивировать».
Другой резон размещения нескольких операторов на одной строке лежит в сфере образования. Автор просит своих студентов операторы, не находящиеся в причинно-следственной связи, писать на одной строке – A
< 1 B
< 2, например. Оператор же, который опирается на предыдущий (предыдущие), следует писать внизу:

A < 1 B < 2 C < A + B

Так можно имитировать параллельные вычисления на однопроцессорной машине: считается, что операторы на одной строке выполняются одновременно, а записанные столбиком – последовательно.
Задание читателям на закрепление пройденного: сделать программу на рис. 6.11 рекуррентной, а на рис. 6.12 – рекурсивной[27].

Расчет чисел Аккермана

Есть более крепкий орешек – числа Аккермана, зависящие уже от двух переменных (см. рис. 6.13 с двойной рекурсией). В среде Mathcad числа Аккермана можно рассчитать только для значений аргументов m и n, находящихся недалеко от нулей («каботажное плавание»). Расчет, например, значения Akk(4, 6) через некоторое время аварийно прерывается – см. рис. 6.13. Рекурсия – это когда программист, сокращая текст программы, перекладывает свои проблемы на плечи машины, которой приходится генерировать длинный ряд новых локальных переменных. Отсюда и сбои. Выход из положения – замена рекурсии на рекуррентность (цикл), что автор и предлагает сделать читателям по отношению к числам Аккермана.
Для закрепления темы рекурсии приводим текст BASIC-программы, решающей известную головоломку «Ханойские башни»[28]
(рис. 6.14):
DefInt N
DefStr X-Z
Declare Sub PUTDISK (N%, X$, Y$, Z$)
Input "Число дисков в пирамиде"; N0
            PUTDISK N0, "A", "B", "C"
End
Sub PUTDISK (N%, X$, Y$, Z$)
DefInt N
DefStr X-Z
If N = 1 Then
                        Print X; "-"; Z
            Else
                        PUTDISK N - 1, X, Z, Y
                        Print X; "-"; Z
                        PUTDISK N - 1, Y, X, Z
            End If
End Sub

BASIC-программа «Ханойские башни»

Суть головоломки. Имеется три стержня, на первый из которых (у нас в программе на рис. 6.14 он маркирован как A) нанизаны диски на манер детской пирамидки: самый большой диск внизу – самый маленький наверху. Предлагается переложить эти диски на второй стержень (C), беря их по одному и не кладя большой диск на маленький. Для временного складирования разрешается использовать третий диск (B). Программе на рис. 6.14 достаточно сообщить только число дисков в пирамиде N. После запуска программа будет возвращать порядок перекладки дисков:
N=2: A-B, A-C и B-C (три хода)
N=3: A-C, A-B, C-B, A-С, В-A, B-C и, наконец, A-C (семь ходов)
N=4: …(15 ходов) и т.д.
Число перестановок в общем случае равно 2N-1. Задача с N дисками легко сводится к задаче с N-1 дисками, а задача с N-1 дисками легко сводится к задаче с N-2 дисками и т.д. до задачи с двумя дисками, которая решается просто – A-C (см. на рис. 6.14 фрагмент программы If N = 1 Then Print X; "-"; Z). Отсюда и рекурсия в программе на рис 6.14.
Задание читателям[29]
– переписать BASIC-программу на рис. 6.14 для Mathcad. Подводный камень: BASIC-программа оператором Print выдает результат из подпрограммы. В языке Mathcad это сделать невозможно – там допустимо сначала полностью заполнить матрицу, и только потом вывести ее на дисплей.
По легенде тибетские монахи уже несколько тысячелетий перекладывают 64 золотых диска, нанизывая их на алмазные стержни. Когда головоломка будет решена и на стержне C окажутся все диски, наступит конец света. Спасает нас лишь то, что при 64 дисках для решения головоломки потребуется:

Это без учета ложных ходов и времени, необходимого на ручной или компьютерный расчет порядка перестановки дисков.

Размерность в программе

Тип числовой переменной в среде Mathcad, как уже было отмечено в этюде 1, в какой-то мере заменяется размерностью хранимой величины, что очень удобно в инженерных расчетах. По программе на рис. 6.15 рассчитывается площадь треугольника (пункт 1). Аргументами функции Площ_треуг могут быть величины с разной размерностью длины (метры – m, сантиметры – cm, дюймы – in). Система Mathcad сама в них разберется, сделает нужные пересчеты и выдаст правильный результат в выбранной пользователем системе единиц (кг-м-с, г-см-с, СИ или британская).
Система Mathcad, кроме того, ведет контроль размерностей и не позволяет складывать, например, метры с килограммами или секундами (см. соответствующее встроенное сообщение об ошибке в конце пункта 1 на рис. 6.15).
Функция в среде Mathcad, как уже отмечалось, может возвращать несколько значений, объединенных в вектор. Программно заданная пользовательская функция в пункте 2 на рис. 6.15 возвращает значение периметра и площади треугольника. Но если пользователь захочет сделать размерными аргументы, чтобы функция вернула ему значение периметра и площади треугольника с соответствующими размерностями (пункт 3), то его ждет неудача. При этом будет выдано дезинформирующее сообщение об ошибке: «Несоответствие единиц измерения». Пользователь будет думать, что он складывает метры с килограммами, как в пункте 1. Но причина в другом – вектор в среде Mathcad может хранить переменные только одной размерности. Из-за этого нам уже пришлось отказаться от размерностей при решении задачи о равновесии балки – сравните рис. 1.15 и 1.16.
Можно заставить функцию выдавать две величины не сразу, а попеременно – в зависимости от значения дополнительного аргумента (пункт 4): если i = “Периметр”, то функция Параметры_треуг возвращает периметр треугольника, если i = “Площадь”, то – площадь. Но и здесь работа с размерностями будет приводить к сбоям – см. пункт 5 на рис. 6.15. Функция Параметры_треуг всегда возвращает размерность переменной из последней строки программы.

Ошибок в среде Mathcad, как и в любой другой программной среде, достаточно. Автор акцентирует внимание на этой ошибке по двум причинам. Во-первых, автор когда-то убил уйму времени, отлаживая программу, подобную программе на рис. 6.15, и не понимая, в чем суть ошибки. Во-вторых, дал об этом знать разработчикам Mathcad, но в восьмой версии эта ошибка почему-то не была исправлена. Кстати, об ошибках…

Считается, что по-настоящему красивая женщина («чертовски красивая») непременно должна иметь внешний дефект (ошибку Природы), небольшой, но сразу бросающийся в глаза: вздернутый нос, родинка, веснушки... Такие «украшения» лишний раз напоминают о том, что это не богиня, от которой лучше держаться подальше, не бездушная «кукла восковая», а земная женщина. Вот хрестоматийный пример: Наталья Николаевна Пушкина (урожденная Гончарова) – петербургская красавица, которая тем не менее чуть-чуть косила[30]. А вот другой пример – Шекспир воспел «смуглую леди сонетов» в те времена, когда белизна лица считалась непременным атрибутом женской красоты.

Слово «чуть-чуть», только что промелькнувшее в тексте, напоминает о кратком, но точном определении художественного вкуса: «Искусство – это чувство меры». Рафинированное произведение искусства, созданное на основе чистых канонов, находится как бы в неравновесном состоянии. Маленький щелчок («глюк» в программе, родинка на лице красавицы или ее легкое косоглазие, кривая колокольня в Пизе, корявый автограф в углу картины или темный штрих в биографии художника или программиста[31], на худой конец) сталкивает эту шаткую балансирующую конструкцию либо в чулан поделок (кич), либо в сокровищницу шедевров.

А вот еще пример, поворачивающий проблему на новую грань, где пересекаются плоскости формы и содержания. Сергей Довлатов в своих записках упоминает об известном профессоре-филологе с такими косыми глазами, что с ним трудно было общаться – непонятно, в какой глаз нужно смотреть. Этот профессор, прикрывая рукой левый глаз, говорил собеседнику: «Смотрите в правый. На левый не обращайте внимания. Левый – это дань формализму». Хорошо дурачиться, создав предварительно целую филологическую школу – ошибки простительны только в гениальных программах.


Если читатель увидит опечатки или даже ошибки в этой книге, то автор просит, во-первых, сообщить об этом автору, а, во-вторых, перечитать то, что написано выше.

Работа с размерностями вообще требует особой аккуратности. Вот хороший совет при работе в среде Mathcad. Вводить в Mathcad-документ новую переменную лучше оператором «m=» (вывод значения), а не оператором «m:=» (ввод значения). Этим пользователь проверяет лишний раз, не занята ли уже переменная m хранением заданной ранее величины. В Mathcad 7 и 8 этот прием не обременителен, так как в среде этих версий оператор «m=» автоматически (Smart Operator) превращается в оператор «m:=», если переменная m свободна от хранения чего-либо.

Предпроверку переменных особо можно рекомендовать в расчетах с использованием размерностей физических величин[32]. В этом режиме (а он включается по умолчанию) предопределенными (системными) будет огромное число «популярных» переменных (A, c, C, F, g, H, J, K, L, m, N и т.д. – см. приложение 7), хранящих единичные значения физических величин (сила тока, скорость, заряд, емкость, ускорение, индуктивность, энергия, температура, длина, количество вещества и т.д.). В таком расчете «невинное» выражение «m:=3» развалит весь стройный порядок единиц измерения: вместо метров появится черт знает что.

Метод Ньютона I (BASIC): цикл с выходом из середины

На рис. 6.16
приведена BASIC-программа поиска корня алгебраического уравнения методом Ньютона (касательных). Почему мы начали с языка BASIC, ведь этюд посвящен языку программирования Mathcad? Дело в том, что язык BASIC кроме традиционной тройки циклов (цикл с предпроверкой, цикл с постпроверкой, цикл с параметром) имеет и универсальный цикл с выходом из середины: Do [...] If ... Then [...] Exit Do [...] Loop. Эта конструкция наряду с другими преимуществами, о которых будет сказано ниже, позволяет реализовывать алгоритмы в их естественной последовательности. Так, в программе на рис. 6.16 объявляются функции пользователя (анализируемое уравнение y и его производная dy), запрашивается значение начального приближения к корню x и задается значение погрешности TOL. После этого организуется цикл, но не традиционный, а с выходом из середины. В цикле, следуя естественному порядку алгоритма Ньютона, рассчитывается новое приближение к корню (x1), и если оно отстает от предыдущего не более чем на величину заданной погрешности[34], то (Then) задача считается решенной (Exit Do). Если нет, то ведется подготовка к новому приближению (x = x1), а цикл повторяется (Loop).
При реализации на языке Mathcad этот несложный алгоритм обрастает «архитектурными излишествами», так как его приходится реализовывать функцией и «запихивать» в прокрустово ложе цикла while – см. рис. 6.17.

Метод Ньютона II: цикл с предпроверкой

Цикл с предпроверкой (цикл while) требует, чтобы булево выражение заголовка было определено еще до входа в цикл. А этого нет при поиске корня методом Ньютона. Приходится до входа (и для входа) в цикл писать x1 ¬ x + 2 × TOL. Подобным образом лгут детям (а машина тоже в каком-то смысле дитя), заставляя их что-то делать. Строку x1 ¬ x + 2 × TOL можно уподобить стартеру двигателя внутреннего сгорания, работающего, кстати, как и программа на рис. 6.17, циклически. Вот какими аллегориями (дитя, двигатель) обросла наша простенькая программа из-за того, что в языке Mathcad нет цикла с выходом из середины. На рис. 6.17 можно отметить и другую ненатуральность программы – постановку телеги впереди лошади: в цикле сначала приходится готовиться к новому приближению (x1 ¬ x), хотя еще не ясно, понадобится оно или нет, а только потом проводить его.
Операторы break, continue и return, введенные в Mathcad, призваны вернуть программе на рис. 6.17 ее естественность, но...

Метод Ньютона III: имитация цикла с выходом из середины

BASIC-конструкция Do ... Loop (см. рис. 6.16) на рис. 6.18 превратилась в конструкцию while 1 ..., которую на латинский язык можно перевести как «ad calendas greaces» – «до греческих календ». Здесь, как и в программе на рис. 6.17, пришлось идти если не на обман, то на натяжку: «выполняй, пока рак на горе не свистнет».
Оператор continue отличается от оператора break тем, что передает управление не в хвост, а в гриву (начало) цикла[35]. Но в документации и в файлах помощи Mathcad нет примеров, обосновывающих использование оператора continue. Не смог придумать их и автор.
История с вводом в Mathcad операторов break и continue и return подтверждает старую истину о том, что «нет ничего практичнее хорошей теории». И вот почему.
Вышеприведенный анализ циклов на языке Mathcad имеет не только сугубо практический, но и чисто теоретический аспект. Как известно, набор управляющих конструкций любого структурного языка ведет свою родословную от основной структурной теоремы Дейкстры, объявившей войну меткам: «Алгоритм любой сложности можно реализовать, используя только цикл while и альтернативу». Автор потратил уйму времени и сил на поиск доказательства этой теоремы в статьях или книгах, но так ничего и не нашел. А вот показать, что данная теорема не верна, можно в два счета – см. рис. 6.19 и рис. 6.20. Эти программы решают уже известную нам задачу о корне алгебраического уравнения, но другим методом – методом половинного деления. Его алгоритм – простейшая иллюстрация теоремы Дейкстры: цикл (while) приближения к корню, в которой вложена альтернатива (if ... ). Если корень правее центра интервала a-b, то к нему (к центру) подтягивается левый край (a ¬ x), если нет – правый (b ¬ х).

Метод половинного деления I (Mathcad)

В программе на рис. 6.20 альтернатива программы на рис. 6.19
заменена на два цикла while, операторы тела которых попеременно выполняются либо раз, либо ни разу, что регулируется булевой переменной Flag.

Панель программирования Mathcad

Щелчок по одной из этих кнопок создает на дисплее заготовку соответствующей программной конструкции.
Опишем их.
Кнопка  – это команда добавления строки в программу, в тело цикла, в плечо альтернативы и т.д. Этим действием снимается вышеупомянутое ограничение на число операторов во вложенных конструкциях языка:
Было

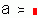
стало

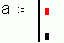
Вертикальная линия объединяет отдельные операторы в операторный блок с одним входом и одним выходом, который выполняется как единый оператор (один из трех атрибутов структурного программирования). Какое-то подобие операторного блока пользователь Mathcad часто выделяет и в беспрограммном документе, реализуя, например, метод последовательных приближений (см. пункт 6 на рис. 5.1).
Кнопка  – это оператор присвоения значения локальной переменной. На языке Pascal мы пишем А := В + С, на языке BASIC – А = В + С, а на языке Mathcad – А ¬ B + С. Почему? Сначала опять же приходится недоумевать, но потом понимаешь, что без знака «¬» программа превратилась бы в нечто невразумительное, режущее глаз программиста:
A := A := B + C (Pascal),
А = А = В + С (BASIC)[7].
В Mathcad-выражении:
A := A ¬ B + C
все более-менее ясно: локальной переменной A (она в середине между символами «:=» и «¬») присваивается значение суммы двух переменных B и C, значение которых уже задано выше в Mathcad-документе (глобальные переменные). Затем эта сумма передается глобальной переменной A (она слева от знака «:=»).
Простейший пример, показывающий разницу между глобальной и локальной переменной:

Негативное изображение переменной В будет свидетельствовать о том, что ее значение вне программы (В ¬ 3) неопределенно[8]. Благодаря локальным переменным можно создавать объемные Mathcad-документы, поручая разработку отдельных функций и операторов разным программистам и не заботясь о разделении переменных: в разных программах переменные могут совпадать по имени, но при этом они не будут перебегать дорогу друг другу (технология программирования «сверху вниз»). С локальными переменными мы, кстати, сталкивались и ранее: примеры индексы i, j и др. в операторах суммы или произведения (см., например, конец рис. 3.14).

Итак, локальная переменная распространяет свое действие только на программу, а глобальная – на весь документ (на низ документа). Но в среде Mathcad есть инструментарий, позволяющий переменным, пользовательским функциям и операторам проникать и в другие документы, но с их, так сказать, согласия. Представим такую ситуацию. Конкретный пользователь создал функции, которые помогают ему быстро решать задачи в конкретной научно-технической области. Решая очередную задачу, пользователь должен в начале документа записать все нужные для расчета функции. Среда Mathcad предоставляет пользователю и другое решение данной проблемы. В новом документе можно сделать ссылку (Reference) на документ (файл с расширением *.mcd), хранящий нужные пользовательские функции, операторы и переменные. Документ, на который ссылаются, может в данный момент не быть открытым, а просто храниться на диске. После этого к создаваемому документу как бы приписывается сверху еще один документ. Пример ссылки на другой Mathcad-документ можно видеть на рис. 6.29, 6.30 и 6.49.

Нажав на кнопку , мы получим на экране заготовку цикла[9]

с предпроверкой – слово while с двумя пустыми квадратиками:



В первый квадратик (правее while) нужно будет записать булево выражение (переменную), управляющее циклом, а во второй (ниже while) – тело цикла, операторы которого будут выполняться, пока булево выражение возвращает значение «Да» (в среде Mathcad – это числовое значение, отличное от нуля). Если в теле цикла более одного оператора (а это основное отличие оператора while от вышеупомянутой функции until), то нужно воспользоваться кнопкой Add Line (см. выше).

Метод половинного деления II (Mathcad)

Кроме того, в программе на рис. 6.20 проведена чистка цикла, в теле которого значение анализируемой функции рассчитывается всего раз. В программе на рис. 6.19 это делалось два раза. Второе изменение в программе на рис. 6.21
по сравнению с программой на рис. 6.19
состоит в том, что не используется функция Хевисайда. Букву Ф у нас принимают не за греческую букву «фи», а за русскую букву «эф» и делают ошибку, которую трудно понять и поэтому тяжело исправить. Функцию Хевисайда заменяет произведение значений анализируемой функции на концах вилки. Булева операция And в программе на рис. 6.20 вызывается не в виде функции And(..., ...), а древовидным оператором.

Метод половинного деления III (QBasic)

В аналогичной BASIC-программе (на рис. 6.21 она вписана в структурную диаграмму) также обошлись без альтернативы. Более того, удалось избавиться и от переменной-диспетчера Flag, заменив два цикла while на один цикл, но с двумя выходами из середины – одним условным, а вторым безусловным.
Весь фокус программ на рис. 6.20 и 6.21
в том, что альтернатива – это средство ускоренного «путешествия» по алгоритму только в одну сторону (сверху вниз и слева направо), а цикл – в обе. Отсюда и ненужность (в теоретическом плане, конечно, а не в практическом[36]) альтернативы. Цикл Do [...] If
... Then [...] Exit Do [...] Loop можно считать гибридом цикла и альтернативы.
Доказательством теоремы Дейкстры может служить факт, что до сих пор не было случая, когда задуманный алгоритм нельзя было бы реализовать, используя только цикл и альтернативу[37]. Если альтернативу исключить, то основная структурная теорема должна звучать так: «Алгоритм любой сложности можно реализовать, используя только цикл». Вот это-то теоретическое положение вводом операторов break, continue и return подсовывает задним числом язык программирования Mathcad под свой фундамент. Обращаю внимание на несовершенный вид глагола – «подсовывает», а не «подсунул» – цикл с выходом из середины на языке Mathcad осуществим через насилие над циклом while (рис. 6.18). При этом приходится писать в заголовке цикла какую-нибудь тривиальную истину: «Волга впадает в Каспийское море».
Теорему Дейкстры следует «понизить в звании» и называть леммой, то есть вспомогательной теоремой, служащей для доказательства основной.
Здесь мы вернулись к спорам, бушевавшим лет 30 назад. Операторы break, continue и return, введенные в язык Mathcad, дали нам повод напомнить о них. Эти операторы по принципу «и вашим и нашим» примирили сторонников и противников оператора перехода к метке.

Задача о рыбаках и рыбке: «беспрограммное» решение в среде Mathcad

На рис. 6.22 показано, как задача решается методом последовательных приближений – задается первое приближение к ответу (50 рыб), а затем от этого числа отнимается по единице до тех пор, пока убывающий улов не будет представлять собой целочисленный ряд: было 25 рыб (искомый ответ задачи), первый рыбак выбросил одну, забрал треть и оставил товарищам 16 рыб (по 8 каждому); второй рыбак (не зная, что первый ушел) оставил 10 рыб, а третий – 6. Задача решена, но с применением «ручной» работы, состоящей в наблюдении за значениями переменной Улов и в изменении (уменьшении на единицу) значения переменной Ответ. (Блоки операторов, фиксирующих действие трех рыбаков, можно не дублировать, как это сделано на рис. 6.22. Достаточно уменьшать[38]
значение переменной Ответ и следить за значениями переменной Улов).
Попробуем автоматизировать поиск ответа в задаче о рыбаках и рыбке.
‘ 1. Исходная неструктурированная Basic-программа
Input "Предположение"; Ответ
label: Улов = Ответ
            For Рыбак = 1 To 3
                        Улов = Улов – 1
Улов = Улов - Улов / 3
                        If Улов > Int(Улов) Then Ответ = Ответ - 1: Goto label
            Next
Print "Ответ "; Ответ; “рыб”
‘ 2. Первый шаг структурирования - разбег
Input "Предположение"; Ответ
Ответ = Ответ + 1 ‘ Шаг назад
label: Ответ = Ответ - 1 ‘ Шаг вперед
            Улов = Ответ
            For
Рыбак = 1 To
3
                        Улов = Улов – 1
Улов = Улов - Улов / 3
                        If Улов > Int(Улов) Goto label
            Next
Print "Ответ "; Ответ; “рыб”
‘ 3. Второй шаг структурирования – ввод признака
Input "Предположение"; Ответ
Ответ = Ответ + 1
label: Ответ = Ответ – 1
Улов = Ответ
            Поделили = "да" ’ Признак дележа улова
            For Рыбак = 1 To 3
                        Улов = Улов – 1
Улов = Улов - Улов / 3
                        If Улов > Int(Улов) Then
Поделили = “нет”
            Next
If Поделили = “нет Goto
label
Print "Ответ "; Ответ; “рыб”
‘ 4. Третий шаг структурирования – отказ от метки
Input "Предположение"; Ответ
Ответ = Ответ + 1
Do ’ Начало цикла с постпроверкой
            Ответ = Ответ – 1
Улов = Ответ
Поделили = "да"
            For
Рыбак = 1 To
3
                        Улов = Улов – 1
Улов = Улов - Улов / 3
                        If
Улов > Int(Улов) Then
Поделили = “нет”
            Next
Loop Until Поделили = "да" ’ Конец цикла
Print
"Ответ "; Ответ; “рыб”

BASIC-программы решения задачи о рыбаках и рыбке

На рис. 6.23 представлены четыре Basic-программы, решающие задачу о рыбаках и рыбке в автоматическом режиме: оператор Input запрашивает первое приближение (те же 50 рыб, к примеру), а оператор Print выдает ответ – 25 рыб. В первой BASIC-программе один к одному реализован алгоритм «ручного» расчета: как только в теле цикла с параметром (три последовательных ухода рыбаков) переменная Улов обретает дробный «хвостик» (встроенная BASIC-функция Int этот «хвостик» обрезает; ее Mathcad-аналог – функция floor), то (Then) предположение уменьшается на единицу (Ответ = Ответ - 1), а управление программой передается к оператору, помеченному меткой (Goto label). Прежде чем эту программу перевести на язык Mathcad, ее нужно освободить от метки[39]. И не только потому, что в арсенале средств программирования Mathcad нет метки и операторов условного и безусловного перехода к метке, но по другим причинам, не связанным с Mathcad. В нашей коротенькой программе-безделушке (пункт 1 на рис. 6.23) метка вполне уместна и естественна, но если программа с метками разрастается, то в ней становится трудно разбираться и ее практически невозможно отлаживать и расширять. Программа, как справедливо подчеркивают адепты структурного программирования, становится похожа на спагетти: вытаскиваешь (вилкой) блок операторов для отдельной отладки или компиляции, а к нему намертво привязаны нити (макаронины) Goto-переходов. Кроме того, такую программу невозможно создавать группой разработчиков (технология снизу вверх). Первые реализации языка Pascal совсем не имели меток, так как этот язык разрабатывался Н.Виртом в первую очередь для обучения студентов структурному программированию. Метка появилась только в поздних версиях этого языка. Так от детей в период, когда они учатся жить (выживать!), прячут спички.
Первый шаг структурирования BASIC-программы на рис. 6.23 – это превращение конструкции:
If
Улов > Int(Улов) Then
Ответ = Ответ - 1: Goto label
в оператор условного перехода к метке:
If Улов > Int(Улов) Goto label

Это сделать несложно (см. пункт 2 на рис. 6.23), применив в программе технику разбега спортсмена перед прыжком: шаг назад от черты-метки (Ответ = Ответ + 1) и разбег (Ответ= Ответ - 1). Структурирование программы, как правило, несколько усложняет алгоритм: «За все нужно платить!», «Красота требует жертв!» и т. д.

Второй шаг структурирования – это вытаскивание оператора безусловного перехода из тела цикла For. Для этого в программу (см. пункт 3) вводится вспомогательная булева переменная-признак Поделили, а в теле цикла оператор условного перехода к метке заменяется на оператор «альтернатива с одним плечом» (одна из основных структурных управляющих конструкций). Сам же оператор условного перехода «сползает» вниз. После этого в программе «вырисовывается» еще одна основная структурная управляющая конструкция – цикл с постпроверкой, который в третьем варианте на рис. 6.23 реализован через метку и оператор условного перехода к метке. После этого программу наконец-то можно совсем освободить метки, реализуя алгоритм через цикл с постпроверкой, в тело которого вписан цикл for, а в него ¾ альтернатива с одним плечом (пункт 4).

После всех этих манипуляций четвертый вариант BASIC-программы можно один к одному переписать для Mathcad – см. рис. 6.24. Придется только оформить ее в виде функции пользователя: в языке Mathcad нет операторов Input и Print[40]. Их аналоги в среде Mathcad (операторы - := - и - =) работают, увы, только вне программ.

Mathcad-программа решения задачи о рыбаках и рыбке

На рис. 6.24 показаны вызовы функции Ответ при различных значениях предположений (50, 24, минус 3 и даже минус 30 рыб). Английский физик Поль Дирак придумал не только античастицы, но и «антирыбы»: он сказал, что задача о рыбаках и рыбке решалась неправильно (25 рыб). Правильный ответ – минус две рыбы (плюс две антирыбы): выбрасываем одну – остается минус три, забираем треть – остается минус две и так до бесконечности. Наше компьютерное решение задачи показывает, что и Дирак ошибался: «Поль, ты не прав!» Условию задачи отвечает бесконечный ряд чисел (назовем его «рыбный ряд Дирака») с шагом 27.
Чтобы не прослыть совсем уж полным педантом (программистом-занудой), можно в конец цикла for на рис. 6.24 вставить оператор break if Поделили = ”нет”, прерывающим выполнения цикла for. Если рыбаков будет не трое, а больше (тридцать три рыбака, например – задача для читателя), то этот прием существенно ускорит работу программы (см. главку «Оптимизация Mathcad-программ»).
Можно еще усложнить задачу, заставив любое количество рыбаков выбрасывать или подлавливать любое количество рыб.
Задачу о рыбаках и рыбке можно решать другим способом – перебором с другого конца: задать не начальное число рыб в улове, а предположить, что последний рыбак оставляет две рыбы (меньше не может быть), и увеличивать их число на единицу, если условия задачи не выполняются. Задача будет решаться быстрее, но минус двух рыб, а, тем более, минус 29 рыб мы не получим: «Keep if simple, stupid! – Делай это проще, дурачок!» Человеку психологически трудно спуститься к отрицательным числам в ответе, машина же делает это спокойно, без всяких предрассудков. Не дает отрицательного ответа и аналитическое решение задачи – поиск целочисленных корней одного уравнения с двумя неизвестными.
Остается рассказать о последней кнопке  на панели программирования Mathcad 8 Pro. Нажатие на нее приводит к появлению на дисплее заготовки инфиксного оператора обработки ошибок с двумя операндами:

Суть оператора проста: если при выполнении правого операнда возникнет ошибка, то выполняется левый операнд. Этот оператор позволяет реализовывать в Mathcad-программах метод проб и ошибок.
Автору, как только он познакомился с оператором on error, сразу захотелось испробовать его на простом примере:

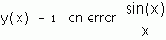
Но оказалось, что объявленная таким образом функция y(х) возвращает нуль, а не единицу при x = 0. Дело в том, что система Mathcad, оптимизируя произведение, выдает нуль, если первый сомножитель равен нулю. Функцию y(х) нужно переписать по другому:

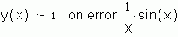
но и эта запись не совсем правомочна. Проще записать:

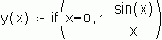
Оператор on error незаменим в тех случаях, когда ошибку сложно локализовать, что иллюстрирует пример на рис. 6.25.

Работа оператора on error

Здесь графически решается неравенство: функция f(x) возвращает нуль не только тогда, когда логарифм меньше единицы, но и тогда, когда делается попытка взятия логарифма от неположительного числа. Можно, конечно, решить квадратное уравнение и обойти ошибку функцией или оператором if, но на рис. 6.25 мы все сделали проще.

Поиск минимума методом золотого сечения

Аргументы функции мин_З_С:

имя функции, у которой ищется минимум (y[42]);

левое значение интервала неопределенности (a);

правое значение интервала неопределенности (b).

Функция мин_З_С возвращает значение аргумента, при котором функция y имеет минимум[43]. Он ищется циклически. Условие завершения цикла – сужение интервала неопределенности до величины, меньшей или равной значению TOL. В цикле интервал неопределенности делится в золотом соотношении, что позволяет при новом приближении к максимуму использовать данные предыдущего приближения. Это вытекает из свойств золотого сечения и позволяет в цикле вычислять только одно значение функции, а не два, как при использовании метода половинного деления (см. рис. 6.55).
Функция мин_З_С протестирована на поиске объема пожарного ведра максимальной вместимости (задача из этюда 2). Функция, связывающая объем ведра с углом вырезки заготовки, задана также программными средствами (а не вложением вспомогательных функций, как на рис. 2.2). С помощью программы поиска минимума ищется максимум за счет изменения знака анализируемой функции. Отсюда можно предположить, что одна из новых встроенных в Mathcad 8 функций ¾ Minimize или Maximize ¾ лишняя. Но это не так – в оптимизационных задачах с ограничениями (см., рис. 2.9 и 2.10) заменить поиск минимума на поиск максимума не так просто.

Поиск минимума многомерной функции

Функция minimum протестирована (рис. 6.28) на решении «четырехведерной» задачи (см. этюд 2, где решались «одно-«, «двух-» и «трехведерные» задачи – поиск оптимального посекторного раскроя круглой заготовки для изготовления одного, двух и трех пожарных ведер с максимальным суммарным объемом). Показано, что четвертое ведро лишнее (как, кстати, и третье – см. рис. 2.7).

Тестирование функции minimum на «четырехведерной» задаче

Алгоритм спуска к минимуму, заложенный в программу на рис. 6.27, ¾ простой и без всяких оптимизирующих хитростей. Так, например, при очередном приближении к минимуму лишний раз рассчитывается значение анализируемой функции в предыдущей точке. Если анализируемая функция простая и ее значение высчитывается быстро, то это повторение мало влияет на общее время поиска минимума. Но что будет, если функция достаточно сложная? Предлагаем читателям доработать программу на рис. 6.27 и исправить отмеченный недостаток. Программа должна запоминать значение анализируемой функции в предыдущей точке приближения и использовать его в новом приближении. Это, кстати, заложено в метод золотого сечения (см. рис. 6.26). А вот более сложное задание. При поиске минимума функции двух переменных мы «перекрещиваем» точку очередного приближения, как бы благословляя успех поиска: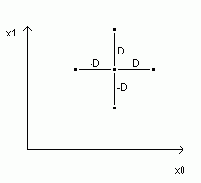

Более оптимальная стратегия может требовать «охвата» очередной точки не крестом, а равносторонним треугольником со стороной D (симплекс-метод; при минимизации функции трех переменных точка помещается внутри тетраэда и т. д.):

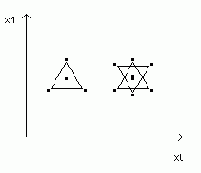
Кроме того, неплохо треугольник (либо звезду Давида или даже пятиконечную звезду – новое задание читателю) при каждом шаге приближения к минимуму ориентировать в пространстве случайным образом, растягивать его вдоль одной из вершин. Этим также можно добиться более оптимальной стратегии поиска минимума.
Описанные ухищрения можно перенести и на задачу с n переменными оптимизации (n-мерная иудейская или пятиконечная звезда!). Все это будет хорошим заданием читателям. Поиск и испытание алгоритмов оптимизации относится к одному из разделов вычислительной (прикладной) математики. В данной книге мы только чуть-чуть заглянули в него.
Читатель может отметить еще одну «неоптимальность» программы на рис. 6.27. Она генерирует не только вектор значений переменных, где функция минимальна, но и целую матрицу М с «историей» поиска, которую потом приходится транспортировать (МТ), определять номер ее последнего столбца (L) и вычленять его (М – см. рис. 6.28). Но перегрузка программы на рис. 6.27 не была напрасна. Как уже отмечалось ранее, программирование в среде Mathcad лишено средств отладки. Простейшее, но тем не менее очень эффективное средство отладки программ – наблюдение за промежуточными результатами. А как раз это в среде Mathcad делать невозможно. И все же – если нельзя, но очень хочется, то можно. Программа, приведенная на рис. 6.27, успешно справляется с довольно-таки сложными задачами (см., например, рис. 6.28). Но если ей подсунуть совсем уж простую функцию – тестовую функцию Розенброка из этюда 3, то при определенных начальных приближениях программа на рис. 6.27 зациклится – ответа от нее не дождешься. В чем тут дело? Ответить на этот вопрос поможет некоторая модернизация программы: прервать ее работу можно не только по условию D £ TOL, но и по дополнительному условию, например, n > 30. После того как число шагов приближения n превысит 30, можно будет просмотреть след поиска минимума функции Розенброка или иной другой (задание читателю).

След при минимизации функции двух переменных

На рис. 6.29 показан след поиска минимума функции х8+y6.
Наполните ванну водой, бросьте туда перышко или какой-нибудь другой легкий предмет и выдерните пробку. Перышко сначала будет более-менее спокойно двигаться к отверстию (первый график на рис. 6.29), а затем закрутится в водовороте (второй график). Наш метод поиска минимума можно назвать не просто методом наискорейшего спуска, а методом наискорейшего спуска воды. Жидкость не просто спускается водоворотом, она всегда вращается в одну сторону. Если даже раскрутить ее в противоположном направлении, то, преодолев насилие, она снова потечет по часовой стрелке. Говорят, что это физическое явление через силы Кориолиса связано с вращением Земли: на экваторе вода в ванне не закручивается, но севернее или южнее экватора она приобретает «правый» (как на рис. 6.29) или «левый» уклон. Автор проверил эту гипотезу: он переслал по е-mail файл с задачей коллеге в Австралию. Все подтвердилось: линии траектории спуска стали закручиваться в другую сторону – против часовой стрелки. Интересно, как они себя поведут на Северном или на Южном полюсах? С водой там все ясно, она вообще не будет течь – замерзнет. А вот что будет с кривыми? К сожалению, у автора нет коллег в Арктике и Антарктике.
Читатель, наверное, уже догадался, что его разыгрывают – этот материал был опубликован в апрельском выпуске одного компьютерного журнала[45].
Но самое смешное в этой истории то, что траектории спуска, показанные на рис. 6.29 в Австралии на самом деле стали закручиваться в другую сторону. Все объяснилось довольно просто: при передаче файла на линии произошел маленький сбой и в программе на рис. 6.27 вместо строки for i Î ORIGIN .. L - 1 появилась строка for i Î L - 1 .. ORIGIN[46]. Вот и все объяснение. Но виноваты в этом все те же силы Кориолиса – магнитные диски винчестеров на серверах и маршрутизаторах Южного полушария вращаются несколько иначе, чем на Северном полушарии. Отсюда и сбои, выявить которые довольно сложно, так как при контрольной обратной пересылке файла ошибка исправляется по принципу «минус на минус дает плюс»[47].

Численное решение задачи Коши (иллюстрация цикла while)

На рис. 6.3 представлены программы численного решения дифференциального уравнения методом Эйлера и методом Рунге ¾ Кутты 4-го порядка. Ядро программ – цикл while. Созданные программно функции Euler и RK4 возвращают значение (в случае системы уравнений – вектор значений) неизвестного выражения, являющегося решением обыкновенного дифференциального уравнения (системы). Аргументы функций Euler и RK4: х1 – значение (вектор значений в случае системы) искомого выражения в начале отрезка интегрирования (решается задача Коши), t1 и t2 – интервал интегрирования, n – число шагов интегрирования и f – правая часть дифференциального уравнения (в случае системы f – вектор-выражение). Функции Euler и RK4 протестированы на расчете числа е (численное решение задачи Коши для дифференциального уравнения х’ = х) и на задаче об эпидемии, которая нами уже была решена встроенными средствами Mathcad (см. рис. 5.2) функцией rkfixed. Программой же на рис. 6.3 мы как бы раскрываем алгоритм работы функции rkfixed. Читатель может доработать функции Euler и RK4 так, чтобы они возвращали решение не только в конечной точке интегрирования, но и на всем интервале интегрирования. Так работает встроенная функция rkfixed.
В программах на рис. 6.3 записаны комментарии – названия функций. Mathcad, к сожалению, не имеет стандартных средств комментирования программ, поэтому мы поступили так – записали в текст программы текстовую константу “Метод Эйлера” и “Метод Рунге ¾ Кутты 4-го порядка”. Комментарии в тексте программ компилятором игнорируются[10], но они помогают читающему программу понять, что здесь имелось в виду, почему тут был использован данный оператор, а не другой и т.д. В программе без комментариев через некоторое время не сможет разобраться (а тем более подправить или развить ее) даже автор.
Кнопка 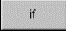 позволяет вводить в программу альтернативу с одним плечом. Так, Pascal-конструкция:
if A > B then C := D
в среде Mathcad будет выглядеть несколько по-арабски (по-еврейски – записана справа налево):

С ¬ D if A > B.

Но если плечо альтернативы – составной оператор, то все встанет на свои места, вернее, будет записано по-китайски (сверху вниз):

Pascal:

if A>B then begin E:=F; F:=G end[11];

Mathcad:

if A>B

E¬F F¬G

Кнопка  превращает неполную альтернативу в полную.

Pascal:	if A > B then C := D else E := F;
Mathcad:	C ¬ D if A > B
	E ¬ F otherwise

Но если в плечах полной альтернативы по одному оператору, то можно воспользоваться не оператором (кнопкой) if, а функцией if:

C¬if(A > B, D, F) или if(A > B, C¬D, E¬F)

Понять, почему в Mathcad не было использовано традиционное слово else, можно, если принять во внимание то, что операторы if и otherwise позволяют записать в программах алгоритмическую конструкцию множественное ветвление. Разберем ее на примере задачи о расчете налогов (федеральный налог США с недельного заработка).

След при минимизации функции трех переменных

На рисунке 6.30 показан объемный след при оптимизации функции трех переменных x8
+ y6 + z4.
В целях все той же отладки можно отслеживать ход поиска минимума функции четырех и более переменных, отображая проекции следа на отдельные плоскости по паре взятых переменных.

Программное решение задачи о краске: оптимизация стоимости краски

Обе программы выдают по шесть вариантов решений, лежащих вблизи максимумов объема и цены краски. Эти решения пересекаются: варианты 6/15 (шесть маленьких и пятнадцать больших) и 13/13 просматриваются в обоих решениях.

Решение задачи о компьютерах с помощью функции Maximize

На рис. 6.33 приведено решение этой задачи линейного программирования с помощью встроенной Mathcad-функции Maximize[49]. Целевые функции (ЦФ) в Mathcad-документе записаны двумя способами: общее число компьютеров (ЦФ1) как функция четырех аргументов-скаляров и стоимость компьютеров (ЦФ2) как функция одного аргумента-вектора. Это позволяет решить задачу двумя способами: «скалярным» (решение 1 по числу компьютеров) и «векторным» (решение 2 по стоимости компьютеров). Второе решение удобно тем, что его методика позволяет легко корректировать задачу: ввод новых переменных и новых ограничений требует лишь внести изменения в векторы КЦФ (стоимость компьютеров) и k (ресурсы по комплектующим) и в матрицу kC (расход комплектующих). Да, вторая методика лучше, но второе решение никуда не годится: как понимать дробные решения ¾ как призыв поставлять компьютеры россыпью или не полностью укомплектованными? Если с первым решением все ясно (можно изготовить максимум 120 компьютеров; какой стоимостью и в каком раскладе ¾ мы еще об этом поговорим), то второе нужно дорабатывать: цифры плана выпуска компьютеров нужно округлять. Дело в том, что функция Maximize не умеет возвращать решение задачи целочисленного линейного программирования. Не совсем умеют ее решать и специально созданные для этих целей программы ¾ вспомним, как в среде Excel решалась задача о краске (см. главку «Как автор продавал программы» в этюде 3).
Целочисленное решение, максимизирующее число компьютеров, получилось, можно сказать, случайно. Так же «случайно» был получен целочисленный план перевозки телевизоров со вкладов в магазины и план выпуска стульев из этюда 2.
Ничего не остается делать, как прибегать к методу перебора, плюсы и минусы которого рассмотрены в этюде 3.

Решение задачи о компьютерах перебором (максимум – стоимость)

На рис. 6.34 и 6.35 приведено решение задачи о компьютерах методом перебора. В программах реализовано три вложенных цикла – по числу типов компьютеров, максимальное количество которых подсчитать несложно: 62 штуки – С2 (лимит по комплектующему №3), 20 – С3 (по №2) и 12 – С4 (по №4). Важное замечание! В программах фиксируются все планы выпуска компьютеров, максимизирующие их число (120 штук) или стоимость (875 600 у.е. – эту цифру можно определить предварительно, отыскивая один план из многих возможных). Что дал перебор и чего не дал бы другой метод решения задачи целочисленного линейного программирования? Оказывается, планов выпуска 120 штук компьютеров целых 156. Можно выпускать не только 100 первых и 20 третьих типов компьютеров (решение, найденное на рис. 6.33), но и 75, 25, 15 и 5. Стоимость компьютеров при этом увеличивается с 560 000 у.е. до 782 500 (см. последний, 155-й столбец).
Функция Maximize «спрятала» от пользователя оптимальный план. Более того, если на рис. 6.33 в качестве начального приближения дать оптимальное первое приближение (75, 25, 15 и 5), то Maximize упорно вернет старый результат – 100, 0, 20 и 0 компьютеров.
На рис. 6.34 выведены первые и последние столбцы матрицы План, содержащей все 156 планов выпуска компьютеров общим числом 120, но с разной стоимостью: от 560000 у.е. (100, 0, 20 и 0 компьютеров разного типа) до782 500 у.е. (75, 25, 15 и 5 компьютеров).
Еще более интересное решение получается при максимизации стоимости компьютеров (рис. 6.35). Дело в том, что при решении задач линейного программирования, как правило, оперируют только неотрицательными значениями переменных (см. ограничение С ³ 0 на рис. 6.33). Но при С1<0 задача может быть сформирована с таким дополнением: «Купи на стороне компьютеры первого типа, разбери их, а дефицитные детали пусти на производство более дорогих машин». Стоимость компьютеров даже с учетом расходов на приобретение машин первого типа может быть выше, чем при традиционном решении. Так и получилось – см. рис. 6.35: матрица План содержит только 2 столбца с «нормальным» решением (1-й столбец: 1, 60, 5 и 10 компьютеров и 4-й столбец: 1, 56, 3 и 11 компьютеров). Максимальная стоимость (883 800 у.е.) получается тогда, когда на стороне покупается 27 компьютеров первого типа.
Метод перебора становится незаменим в том случае, когда задача о компьютерах перестает быть линейной. А это случается, если поставщик комплектующих делает скидку при покупке оптом. Такая динамика изменения цен нами статистически обработана – см. рис. 4.15.

Вспомогательные функции программы «Дуэль»

Участник дуэли, придерживающийся второй (хитрой) тактики, перед выстрелом в цель или перед намеренным промахом должен пересчитать противников, стреляющих лучше его. Эту работу выполняет функция Меткие. В нее заложен такой же алгоритм перебора противников, как и в функции Самый_меткий. Функции Самый_меткий и Меткие в качестве аргументов имеют вектор Меткость, вектор Статус и скаляр Стрелок. Функции при своей работе вызывают логическую функцию And (логическое И ¾ см. пункт 1) с агрументом-вектором, которая возвращает 0 (логическое «нет»), если хотя бы один из элементов вектора (аргумента) равен нулю (см. главку «Mathcad и булевы (логические) функции» в этюде 3). Для реализации математической модели дуэли нам еще понадобится функция логического отрицания Not, определяемая также в пункте 1 на рис. 6.36.
Функция Победитель (пункт 3 на рис. 6.37) возвращает номер победителя в одиночной дуэли. При этом учитывается меткость и тактика каждого участника дуэли (два вектора-аргумента функции Победитель).

Проведение дуэлей

Функция Вероятность_победы (пункт 4 на рис. 6.38) возвращает вектор, элементы которого – это отношение числа побед каждого участника дуэли к общему количеству дуэлей (третий аргумент функции Верояность_победы; два первых аргумента-вектора – это параметры дуэлянтов: их меткость и тактика), то есть вероятность победы.
Теперь, когда все необходимые функции сформированы, можно проводить статистические испытания (см. пункт 5 на рис. 6.38) и фиксировать вероятности побед участников дуэли, исходя из их меткости и тактики. Если увеличивать число побед (переменная N), то, набравшись терпения[51], можно получить результат, близкий к теоретическому.
Задача о трехсторонней дуэли приводится во многих книгах[52]. И что интересно – она там решается неверно. Априори считается, что в этой дуэли самый слабый стрелок (Джон с номером 3) имеет наихудшие шансы выжить. Но если он немного подумает (хитрая техника), то вероятность выйти победителем у него становится самой высокой (52.2(2)%).
Наше решение (см. пункт 5 на рис. 6.38) говорит о том, что у Джона и так самые высокие шансы выжить (44-46%). Начиная хитрить, он мало чего выигрывает, но подводит Билла – своего товарища по несчастью стрелять хуже Сэма.
Откуда такая ошибка в постановке задачи? Дело в том, что у дуэлянтов есть еще одна, нулевая
тактика. Если участники дуэли ничего не знают о стрелковых качествах соперников, то они бьют в первого попавшегося. Здесь вероятность побед можно подсчитать сразу без компьютера: Сэм – 43.48% (1/(1+0.8+0.5)), Билл – 34.78% (0.8/(1+0.8+0.5)) и Джон – 21.74% (0.5/(1+0.8+0.5)) или 100 - 43.48 - 34.78). Но мы составили программу и для этого случая (см. рис. 6.39).

Проведение трехсторонней дуэли (бей в случайного)

Программа 6.39 не считает вероятность побед, а скорее проверяет качество генератора псевдослучайных чисел – добротность функции rnd (см. рис. 6.40).

Налоги США (иллюстрация конструкции «выбор»)

Функции Tax1 и Tax2 (пункт 1) возвращают налог с холостых и женатых по прогрессивной шкале налогообложения (см. график в пункте 3). В данном примере (и во всех других) без оператора otherwise можно обойтись (сравните окончания функций Tax1 и Tax2). Он необходим в тех случаях, когда булево выражение, объединяющее оставшиеся случаи ветвления, трудно сформировать. Оператор otherwise – это гибрид ключевых слов ELSE, ELSEIF и CASE ELSE языка BASIC.
Программы на рис. 6.4 несложно реализовать и без программирования (без операторов if и otherwise), задействовав традиционную Mathcad-функцию if и вкладывая ее саму в себя: if(..., if (..., if(... и т.д. Но программирование функций Tax1 и Tax2 делает их более прозрачными и для понимания, и для редактирования.
В седьмой версии Mathcad появился оператор досрочного прерывания программы, который вводится нажатием кнопки return. Он очень уместен в программе на рис. 6.4 (см. пункт 2): если налогоплательщик мало получает и тем самым освобожден от налога, то нечего и забираться в глубь программы. Кроме того, программой в пункте 2 на рис. 6.4 проиллюстрирована работа текстовой переменной (у нас это S), а также функции error выдачи пользовательского сообщения об ошибке: если к «покрасневшей» функции Tax (последняя строка в пункте 2) подвести курсор, то «выпадет» пользовательское сообщение об ошибке “Укажите правильный статус налогоплательщика”. Дополнительно в функцию Tax на рис. 6.4 введены денежные единицы по принципу «Время – деньги» – см. рис. 1.14.
В программах на рис. 6.4 можно заменить константы и получить функцию для расчета российских налогов. Автор этого не делает по следующим причинам.
Во-первых, за нашей шкалой налогообложения не угнаться. Инфляция с деноминацией и с новой инфляцией делает бессмысленными коэффициенты формул. Кроме того, наши парламентарии считают, что у нас налоги не собираются из-за плохой налоговой системы, в частности, из-за неправильных коэффициентов функции Tax. Но это иллюзии. Налоги у нас не платят в первую очередь из-за того, что люди не хотят отдавать свои деньги неизвестно на что[12]. На больницы, на школы денег нет, а губернатор N-ской области, где эти бедные школы и больницы расположены, еженедельно на своем личном самолете со своей многочисленной свитой летает в Москву. Когда ему говорят, что так делать нельзя, что бюджетные средства в первую очередь должны идти в социальную сферу, то он эти законные претензии называет «дешевым популизмом». Сами же налогоплательщики не желают иметь в качестве посредников таких нечестных людей и стараются отдавать деньги бюджетникам напрямую – собирают деньги на уборку класса, передают конверт с «благодарностью» врачу и т.д. Конечно, это порочная система, но что делать, если люди, призванные распоряжаться нашими деньгами, не могут или не хотят сделать это умно и честно.

Сравнивая нашу шкалу налогов с американской, следует отметить, что в США при больших заработках ставка налога падает с 33 до 28%. Дальновидная политика! В стабильном обществе богатые люди свои доходы не прячут и не проедают, а пускают в дело – расширяют производство, покупают акции и т.д. Кроме того, американская налоговая система нацелена на укрепление семьи. Но мы отвлеклись от основной темы…

Кнопка 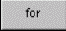 вводит в программы цикл с параметром.

Когда заранее известно, сколько раз нужно выполнить какую-то часть программы (тело цикла), то используют не цикл while, а цикл for, в заголовке которого пишут не булево выражение, а параметр цикла и указывают, какие дискретные значения он должен принимать в цикле. Эти значения можно перечислить через запятую (1, 2, 3.7) или указать диапазоном (2.. 100) или вектором (V). В программах на рис. 6.3, кстати, более уместен цикл for с заголовком for t Î t1, t1 +D.. t2, а не цикл while. При этом программы можно будет несколько упростить, убрав операторы t ¬ t1 и t ¬ t + D (см. рис. 6.5).

Статистические испытания функции rnd на трехсторонней дуэли

Задачу подправили, теперь ее можно развить.
Подсчитанная нами вероятность побед относится к ситуации, когда еще не проводилась жеребьевка по очередности выстрелов: переменная Очередь у нас либо единица, либо минус единица.
Но после жеребьевки шансы Сэма и Билла резко меняются. Дела Билла становятся совсем уж плохи (10-12%), если Джон после своего намеренного промаха передает право выстрела не ему (Очередь = -1), а Сэму (Очередь = 1). И наоборот: Сэм может потерять свои 30%, если после намеренного промаха Джона Билл будет стрелять в Сэма. У Джона вероятность победы (52.2(2)%) не зависит от очередности выстрелов.
Можно придумать и проанализировать четвертую тактику ведения дуэли: Билл и Джон сговариваются
целить в Сэма, убить его, раз он такой меткий, а уж потом выяснять отношения между собой. Инициатором такого сговора, как понимает читатель, скорее всего, будет Билл. Джон пойдет на него, если не смоделирует дуэль на компьютере и не узнает, что из этого может получиться.
Еще одно задание читателю: доработать программы на рис. 6.36-6.40 так, чтобы они были пригодны для дуэли с любым числом участников.
Наше решение задачи о трехсторонней дуэли замыкает троицу новых решений старых проблем. Две другие – задача о рыбаках и рыбке (рис. 6.24 – там мы показали, что Дирак был не прав) и основная структурная теорема (главка «Remake», где мы показали, что альтернатива ¾ это не основная, а всего лишь вспомогательная структурная управляющая конструкция программирования).
Наша модель – не такая уж оторванная от жизни. Дуэли в чистом виде сейчас, к счастью, не проводятся. Но какое-то подобие дуэли со сговором участников наблюдается на рынках, включая финансовые. Кровь там не льется, но случаются инфаркты, лопаются компании, банки, разоряются люди и даже целые страны (Южная Корея, Индонезия, Малайзия, если иметь в виду 1998 год).
Теория игр, тактика поведения участников – это не только интересная, но и очень полезная штука. Недаром в 1998 году лауреатами Нобелевской премии по экономике стали ученые, применившие теорию игр к анализу работы биржи.

И все- таки сама модель чересчур искусственна. Что такое меткость дуэлянта и как ее определить? Проводить реальные статистические испытания? Но одно дело стрелять по мишеням, а другое – целить в живого человека. На дуэлях, как правило, не убивают наповал, а ранят с различной степенью тяжести. Подстреленный дуэлянт, если хватало сил и злости, стрелял в противника (дуэль Пушкина и Дантеса, например). Попытки «приземлить» задачу о дуэлях неизбежно потребуют привлечения аппарата теории нечетких множеств (ТНМ). В этюде 3 мы уже слегка коснулись ее положений.

Меткость дуэлянта – величина нечеткая, «размытая». Никто и нигде не измеряет ее числами, а только оценивает категориями (лингвистическими константами): «мазила», «хороший стрелок», «снайпер» и т.д. Статус дуэлянта – это никакая не булева переменная. Вспомним «консилиум врачей» (из этой компании запомнилась только фельдшерица Жаба) у лежащего без чувств Буратино: «Пациент скорее мертв, чем жив», – «Нет, пациент скорее жив, чем мертв» и т. д.

Оставим дуэли в покое (да и задача уж больно кровожадная[53]) и попытаемся решить что-нибудь попроще – нашу старую задачу об оптимальном пожарном ведре (см. этюд 2).

Оптимальный радиус пожарного ведра

Пункт 1 (рис. 6.41). Матрица mr хранит представления людей об оптимальном (удобном) радиусе основания конуса пожарного ведра (r), выраженном в миллиметрах. Эти данные можно получить так: изготовить много ведер различной геометрии, дать людям поносить их и оценить по такой шкале:

удобное (1);

скорее удобное, чем неудобное (0.67);

скорее неудобное, чем удобное (0.34);

неудобное (0).

Можно принимать во внимание и другие оценки в диапазоне 0-1.
В пункте 1 мы ограничились семью точками, но их может быть намного больше: сколько людей, столько и мнений. Читатель при желании может опросить своих друзей и дополнить матрицу mr новыми столбцами.
Пункт 2. Данные опроса обрабатываются методом наименьших квадратов (см. этюд 4). На рис. 6.41 (как, кстати, и на рис. 6.42 и 6.43) в качестве аппроксимирующей кривой взята кривая нормального[59]
распределения. Получена функция принадлежности по радиусу ведра mr, которая является одним из базовых понятий ТНМ: в привычной математике считается, что некая величина либо принадлежит, либо не принадлежит определенному множеству; в ТНМ допустимо говорить о том, что величина принадлежит множеству в некоторой степени (на столько-то процентов).
Пункт 3. Статистическую обработку принято заканчивать графиком.

Оптимальная высота пожарного ведра

Пункты 4-6 (рис. 6.42) повторяют пункты 1-3, но уже для второго параметра ведра – его высоты.

Оптимальный объем пожарного ведра

Пункты 7-9 повторяют пункты 1-3 и 1-6 для третьего важного параметра ведра – его объема (веса, массы). При этом предлагается дать такие оценки:

ведро легкое (1);

ведро скорее легкое, чем тяжелое (0.67);

ведро скорее тяжелое, чем легкое (0.34):

ведро тяжелое (0).

Данные опроса также обрабатываются с использованием нормального, но уже «однобокого» распределения (см. пункт 9 на рис. 6.43).
При проектировании технических систем, конечно, не проводят опрос общественного мнения, а прислушиваются к экспертам, к лицам, принимающим решения (ЛПР).

Перевернутое» оптимальное пожарное ведро

Пункт 10 на рис. 6.44. является ядром решения задачи: в нем генерируется двухпараметрическая функция принадлежности путем слияния (перемножения) ранее заданных функций принадлежности.
В ТНМ нет понятий сложения, вычитания, умножения и др., лежащих в основе традиционной математики и реализованных в среде Mathcad операторами «+», «-», «×» и т.д. В ТНМ умножение (пересечение множеств, And) заменено на операцию поиска минимума, а сложение (слияние множеств, Or) – на поиск максимума. Математика четких множеств является частным случаем математики нечетких множеств – в программах вместо функции (оператора) And можно использовать функцию поиска минимума, а вместо функции Or – функцию поиска максимума. В среде Mathcad, кстати, нет встроенных функций And и Or[60], но есть встроенные функции min и max – это мы уже отмечали в этюде 3. В нашей задаче функция принадлежности mrh получается путем нечеткого сложения (min) функций mr, mh и mv – нечеткое множество «удобное ведро» лежит на пересечении
трех других нечетких множеств: «удобный радиус ведра», «удобная высота ведра» (пункт 6) и «нетяжелое ведро» (пункт 9).
Пункт 11. Вершина «горы» (поверхность функции mrh[61]) – это то место, где «лежит» самое удобное пожарное ведро.

Проектирование оптимального пожарного ведра

Пункт 12 (рис. 6.45). Искать максимум функции mrh в среде Mathcad можно различными способами (см этюды 2 и 3). Мы поступим так: изготовим от 2 до 10 одинаковых ведер[62] из круглых заготовок различного радиуса R (от 10 до 500 мм с шагом 1 мм). Оптимальным (самым удобным) будем считать то ведро, у которого функция принадлежности mrh максимальна[63].
Даже не очень внимательный читатель заметит неточности, допущенные при решении задачи об удобном ведре. Вот три из них:

ведро никогда не наполняется до краев;

автор уж очень вольно обращается с такими понятиями, как объем, вес и масса ведра, путая их;

не учтен вес пустого ведра, а также материал, из которого оно сделано.

Однако стоит еще раз мельком взглянуть на графики, иллюстрирующие нечеткие множества на рис. 6.41-6.43, чтобы понять важнейшую особенность решения задач с привлечением аппарата ТНМ. Наше решение вычленяет, если так можно выразиться, суть задачи, оставляя без внимания различные мелочи: плотность воды, вес пустого ведра, степень его наполнения и др.
Эта особенность в настоящее время реализована, например, в системах автоматического регулирования, где регуляторы, настроенные с учетом положений ТНМ, более «внимательны» к основному сигналу и менее восприимчивы к шуму. Оказалось, хотя это и кажется парадоксальным, что традиционные «четкие» алгоритмы управления качественно проигрывают «нечетким» либо являются их частными случаями. В теории автоматического регулирования наблюдался некий застой, так как никакие новые алгоритмы не могли сравниться со старым добрым пропорционально-интегрально-дифференциальным (ПИД) алгоритмом (законом) управления. Принципы ПИД-регулирования можно узреть в процедуре принятия решения о выдаче кредита клиенту банка, когда принимающий решение банкир учитывает, во-первых, количество денег на текущем счете просящего (пропорциональная составляющая – чем богаче клиент, тем больше денег ему можно дать в долг), во-вторых, динамику изменения текущего счета (дифференциальная
составляющая – дела клиента на подъеме или в упадке) и, в-третьих, среднее количество денег у клиента за последние, к примеру, пять лет (интегральная составляющая – не занял ли клиент вчера денег на стороне, чтобы создать видимость своего благополучия). Можно учитывать и другие составляющие, но… три – красивое число.

ПИД-алгоритм регулирования как- то незаметно был фетишизирован. Идеи нечеткого управления – это свежая струя в теории автоматического регулирования, основные положения которой в настоящее время подвергаются ревизии. Правда, есть и другое мнение. Некоторые ученые полагают, что использование аппарата ТНМ в теории автоматического регулирования и в кибернетике вообще – это попытки замены одной неопределенности на другую (шило на мыло, грубо говоря). Только и всего. Наблюдающиеся эффекты повышения качества управления скептики объясняют тем, что на регуляторы лишний раз обратили внимание (принцип доброго слова, которое и кошке приятно). Кроме того, некоторые исследователи полагают, что ТНМ (ей всего лишь 30 лет, а открыл ее миру Л.А.Заде – американец иранского происхождения) – это хорошо забытое старое. Мы не случайно перешли к задаче об оптимальном ведре от задачи о трехсторонней дуэли. По традиции, четкие множества принято иллюстрировать кругами с резко оконтуренными границами. Нечеткие же множества – это круги, образованные отдельными точками: в центре круга точек много, а ближе к периферии их густота уменьшается до нуля; круг как бы растушевывается на краях[64]. Такие «нечеткие множества» можно увидеть... в тире ¾ на стене, куда вывешиваются мишени[65]. Следы от пуль образуют случайные

множества, математика которых известна. Оказалось, что для оперирования нечеткими множествами годится уже давно разработанный аппарат случайных множеств...

Мы говорим нечеткое множество. А множество чего? Если быть последовательным, то приходится констатировать, что элементом нечеткого множества оказывается... новое нечеткое множество новых нечетких множеств и т.д. Вернемся к классическому примеру – к куче зерна. Элементом этого нечеткого множества будет миллион зерен, например. Но миллион зерен это никакой не четкий элемент, а новое нечеткое множество. Ведь считая зерна (вручную или автоматически), не мудрено и ошибиться – принять за миллион 999 997 зерен, например. Тут можно сказать, что элемент 999 997 имеет значение функции принадлежности к множеству «миллион», равное 0.999997. Кроме того, само зерно ¾ это опять же не элемент, а новое нечеткое множество: есть полноценное зерно, а есть два сросшихся зерна, недоразвитое зерно или просто шелуха. Считая зерна, человек должен какие-то отбраковывать, принимать два зерна за одно, а в другом случае одно зерно за два. Нечеткое множество не так-то просто запихнуть в цифровой компьютер с классическими языками: элементами массива (вектора) должны быть новые массивы массивов (вложенные вектора и матрицы, если говорить о Mathcad). Классическая математика четких множеств (теория чисел, арифметика и т.д.) – это крюк, с помощью которого человек разумный


фиксирует (детерминирует) себя в скользком и нечетком окружающем мире. А крюк, как известно, ¾ инструмент довольно грубый, нередко портящий то, за что им цепляются. Термины, отображающие нечеткие множества (а их достаточно в этой и любой другой книге – «много», «слегка», «чуть-чуть» и т.д. и т.п.), трудно «запихнуть» в компьютер еще и потому, что они контекстно зависимы. Одно дело сказать «Дай мне немного семечек (зерна)» человеку, у которого стакан семечек, а другое дело – человеку, сидящему за рулем грузовика с семечками.

Можно ли усмотреть некий кризис в теории и практике программирования, связанный с противоречим между четкой структурой программ (данных) и нечетким миром? Следует ли разрабатывать «нечеткие» языки программирования для реализации «нечетких» алгоритмов и для размещения «нечетких» данных? Мнения здесь разные. Программисты (а за ними последнее слово) худо-бедно научились «запихивать» нечеткий мир в строго детерминированный компьютер. Пример на рис. 6.41-45.

Перевод чисел из арабской в римскую систему и наоборот

Так было написано во втором издании книги про Mathcad 7. После выхода книги в свет автор получил решение от Артема Михайлюка, студента Киевского политеха (см. вторую половину рис 6.46). Он же прислал и совсем короткое решение – см. первую половину рис 6.47.

Работа банкомата

Операции по переводу чисел мы проводим каждый день по многу раз, расплачиваясь за покупки. Алгоритм перевода чисел может быть применен, например, в работе банкомата (см. вторую половину рис 6.47).

Окно отладки Mathcad-документа в бета-версии Mathcad 8 Pro

Можно предположить, что если курсор помещался в рамках программного блока, то выводился список локальных переменных программы и выполнялись другие отладочные операции. Но эта таблица была «мертва», а в последующих бета- и в коммерческой версиях Mathcad 8 ее совсем не стало[81].
Тем не менее потребность в отладке программ осталась, и мы о ней поговорим.
Существует две категории ошибок в программах. Ошибки первой категории связаны с неправильным обращением к функциям и операторам Mathcad, формирующим программу. Вот типичное сообщение дефектной программы: «Индексы переменной-вектора (матрицы) вне оговоренных пределов!» Вторая категория ошибок связана с дефектом самого задуманного алгоритма: программа работает без аварийных остановов, но выдает совсем не то, что от нее ожидалось.
Так или иначе, программу нужно «обезжучивать» – искать и удалять ошибки в ней. Вот семь советов на этот случай:
1. Прежде чем писать Mathcad-программу стоит «прощупать» ее основные операторы и порядок их выполнения в «беспрограммном» режиме. Мы так уже поступали, решая задачу о рыбаках и рыбке (рис. 6.22-6.24), например. А вот более «серьезный» пример. На рис. 6.49-6.50[82]
показано, как в среде Mathcad определяется коэффициент полезного действия (кпд) цикла Ренкина, где из котла в турбину поступает перегретый (острый) пар; отработавший (мятый) пар сбрасывается в конденсатор, из конденсатора вода насосом закачивается обратно в котел: так замыкается простейший цикл работы воды и водяного пара. Необходимо определить кпд этого цикла (отношение полезной работы турбины к затраченному теплу) в зависимости от его параметров: от температуры и давления острого пара и давления в конденсаторе (пункт 2 на рис. 6.49). Для расчета нам потребуются термодинамические функции воды и водяного пара: в пункте 3 делается ссылка (команда Reference… в меню Insert) на Mathcad-документ, их хранящий. Сама методика формирования этих функций (одно- и двухмерная сплайн-интерполяция) описана в этюде 4. После такой ссылки кпд цикла рассчитывается по несложным формулам, вытекающим из закона сохранения энергии.

Расчет кпд цикла Ренкина (ручной режим – начало)

Если теперь поменять параметры цикла (пункт 2 на рис. 6.49), то измениться и кпд[83]
(конец пункта 3).

Расчет кпд цикла Ренкина (ручной режим – продолжение)

Этот расчет (отлаженный и протестированный – в Mathcad-документе на рис. 6.49-6.50 выведены для контроля значения всех переменных, задействованных в расчете) целесообразно сгруппировать в функцию-программу (пункт 4.1 на рис. 6.51), по которой очень просто получить расчетные таблицы (пункт 4.3 на рис. 6.52) или графики (пункт 4.3).

Расчет кпд цикла Ренкина (функция пользователя)

При формировании функции следует не писать операторы заново, а копировать их из отлаженного документа, дабы не наделать новых ошибок.

Расчет кпд цикла Ренкина (работа функции пользователя)

Эту функцию можно использовать в новых расчетах, например, при определении реального, а не теоретического кпд реальной тепловой электростанции[84].
Если в программе есть цикл (не термодинамический, а цикл выполнения блока операторов), то его можно развернуть: дублировать операторы блока или вести расчет по этому блоку столько раз, сколько нужно. Так мы поступали, «беспрограммно» решая задачу о рыбаках и рыбке (рис. 6.22) и краевую задачу об эпидемии (рис. 5.1-5.4). Кроме того, не следует забывать о встроенных в Mathcad-функцях if и until, реализующих основные структурные конструкции (выбор и повторение) вне программ. На рис. 6.1 с помощью этих функций «запрограммирован» сложный алгоритм – поиск корня алгебраического уравнения методом половинного деления.
2. Да, в среде Mathcad специализированных средств отладки программ нет. Но они есть в других популярных программных средах: Visual Basic, Visual C, Delphi: и др. Задуманный алгоритм можно сначала реализовать и опробовать в «настоящих» программных средах, а потом уж переписать для Mathcad. Так мы поступали, решая задачу о рыбаках и рыбке (рис. 6.23 и 6.24) или составляя программы поиска корня алгебраических уравнений методом половинного деления и методом Ньютона, а также при поиске минимума методом золотого сечения. Автор задачу о трехсторонней дуэли (рис. 6.36-6.40) сначала поставил, а, главное, отладил в среде языка Visual Basic, а уже потом переписал для Mathcad, где это сразу сделать не удалось.
Воспользоваться этим советом можно лишь в том случае, если в программе нет специфических Mathcad-операторов и функций, отсутствующих в «настоящих» языках.
3. Создавая программу-функцию, на первом этапе стоит сделать так, чтобы она возвращала не только значение «одноименной» переменной, но и некоторых других, задействованных в расчете. Для этого достаточно в конец программы поставить не имя главной переменной, а какой-либо локальной, вспомогательной. Можно все переменные, задействованные в расчете, объединить в вектор и выдать их все на дисплей.

В Mathcad- программу можно вставлять своеобразные точки останова (BreakPoint): операторы return X, где X – это какая-либо локальная переменная программы. После отладки эти операторы убираются совсем или нейтрализуются таким оператором: return X if 2<1.

Если программа зацикливается и ее приходится прерывать нажатием клавиши Esc (текущие значения локальных переменных при этом просмотреть, увы, невозможно), то можно посоветовать в подозрительный цикл вставить дополнительный счетчик. Расчет будет безаварийно завершен, когда значение счетчика достигнет заданной программистом величины.

4. Если функция имеет ограниченный набор значений аргументов и/или возвращает ограниченный набор значений, то стоит не полениться и протестировать функцию глобально. Так, на рис. 3.14 в этюде 3 одноместные, двуместные и трехместные логические функции при тестировании возвращают все, что от них требовалось: у функции Not(x) два значения, у функций And(x1, x2) … AntiOr(x1, x2) – четыре значения, а у функции Решение(х1, х2, х3) – восемь.

5. Случай, описанный в пункте 4, довольно редкий. Если аргументы функции имеют действительные значения[85]

и (или) она возвращает действительные числа, то стоит проверить работу новоиспеченной функции в «экстремальных условиях» – на границах допустимых значений.

6. Вот хорошее правило: после создания программы ей нужно «подсунуть» условия задачи, решение по которым заранее известно. Так, на рис. 6.17-6.20 Mathcad-программы возвращают корни алгебраического уравнения, используя различные способы (метод половинного деления, метод Ньютона, метод секущих). Анализируемое уравнение у нас было простое: х2 - 3 = 0, корни которого известны заранее: плюс-минус квадратный корень из трех. На рис. 6.5 показаны программы решения обыкновенных дифференциальных уравнений и систем методом Рунге ¾ Кутты. Прежде чем с помощью этих функций заняться решением задачи о развитии эпидемии, мы «потренировались» на «кошечках»: рассчитали с их помощью значение основания натурального логарифма (число е).


7. Решая поставленную задачу, нужно постараться разбить ее на отдельные блоки и оформить их в виде отдельных коротких программ[86]. Это позволит локализовать ошибку и облегчить ее поиск. Объемная Mathcad-программа, в которую вкралась ошибка (ошибка алгоритма или ошибка в использовании инструментов Mathcad) – это что-то неисправимое ¾ «вещь в себе». Так, решая задачу о трехсторонней дуэли (рис. 6.36-6.40), мы выделили в отдельные функции такие действия стреляющего, как определение самого меткого противника и пересчет противников, стреляющих лучше[87]. Эти функции были протестированы и только потом стали вызываться из основной программы.

Разбивать на отдельные блоки программу целесообразно не только для оформления в функции, но и просто для отладки, для конструирования. Mathcad в этом отношении обладает уникальными возможностями: отдельные блоки программы (тело цикла, плечи альтернатив) из программы можно изъять и расположить вокруг. На рис. 6.53 изображена «разъятая» программа поиска минимума методом золотого сечения (ее рабочий вариант см. на рис.6.26). В самой же программе остались «местодержатели» (placeholder).

Разъятая Mathcad-программа

Программы можно не только «обезжучивать» (отлаживать), но и «нажучивать». В стародавние времена, когда программы в ЭВМ вводили не их авторы, а девочки-перфораторщицы и готовые тексты программ из-за этого содержали много «глупых» ошибок типа 5 вместо S, 1 (один) вместо I («и» латинское) и т.д., практиковался (больше, конечно, в теории, а не на практике) довольно оригинальный способ отладки по принципу «клин клином вышибают». Если нужно было узнать, сколько в программе осталось «жучков», то в нее... вводили еще сотню ошибок. Затем другой человек эту программу отлаживал. И если оказывалось, что он, к примеру, выловил 50 специально введенных ошибок и 10 первоначальных, то с определенной долей вероятности можно было считать, что в программе осталось еще с десяток «натуральных» жучков-ошибок. Кстати, подбор искусственных ошибок – это и наука, и искусство высокого класса, а сам процесс отладки очень трудоемкий, способный довести программиста до белой горячки. Недаром по-английски to go bugs означает сойти с ума. Очень часто бывает проще стереть написанную программу и ввести ее заново, чем искать в ней ошибки. Один коллега автора долго не мог понять, что происходит в такой коротенькой цепочке операторов:
a := 3                     b := 1              a - b= -3
Если от трех отнять единицу, то должна выйти двойка, но никак не тройка, да еще с минусом? Ответ оказался прост, но эта простота была уж точно «хуже воровства». Дело в том, что в приведенном примере не b вычитается из a, а переменная a умножается на минус b. В среде Mathcad начиная с 7 версии, если константа умножается на переменную, то знак умножения можно опускать. Этот прием особо удобен при вводе размерностей 5m, 3 kg и т.д. – человек еще до общения с компьютером привык не ставить тут знака умножения. В вышеприведенном примере сначала было записано 3 b=, но потом тройку заменили на переменную a, а b на минус b. Услуга Mathcad (программисту не нужно вводить знак умножения) здесь оказалась «медвежьей». Вот еще иллюстрации принципа «Не верь глазам своим!»:

MT – что это? Транспонированная матрица M или матрица (вектор, скаляр) M в степени T?

Аi ¾ это i-й элемент вектора А или i – это часть имени переменной с текстовым индексом (набираем A.i, получаем А i)?

В переменной Стрелок первая буква английская «си» или русская «эс»?

Свести с ума может и такая «первоапрельская» шутка. Программист на минутку отлучился от компьютера, а «шутник» вверху Mathcad-документа, на правом, невидимом листе написал sin(x):=cos(x), e:=p или что другое из области «crazy[88]». Можно у отдельной переменной незаметно поменять шрифт с Variable на User1, например – эффект тоже будет очень интересным. В таких ситуациях не стоит пытаться отыскать ошибку – лучше начать все с «чистого листа»: создать новый пустой рабочий документ и в него постепенно переносить отдельные фрагменты «сумасшедшего» Mathcad-документа, отлавливая ошибку…

Поиск корня методом прямого перебора

Не трудно подсчитать, сколько раз в программе на рис. 6.54 вызывается функция y(x) – считать не будем, а просто скажем, что очень много. Наша тестовая функция (см. пункт 6 в главке «Отладка Mathcad-программ») простенькая и компьютер обрабатывает ее за микросекунды[90]. Но что будет, если функция сложна, отображает математические модели реального мира и работает довольно долго? Тут пригодится метод половинного деления (метод Ньютона, метод касательных и др. – см. программы 6.16-6.21). Если поиск корня методом перебора требует N вычисленных значений анализируемой функции, то метод половинного деления – всего лишь log2N.
Методом половинного деления[91]
можно искать и минимум функции на отрезке a-b (рис. 6.55):

Поиск минимума функции методом половинного деления

В программе на рис. 6.55 значение анализируемой функции в цикле высчитывается дважды – чуть левее и чуть правее середины интервала неопределенности. При реализации метода золотого сечения (рис. 6.26) для поиска минимума значение анализируемой функции в цикле высчитывается всего лишь раз, но сама программа становится несколько сложнее. Но если необходимо найти глобальный (самый минимальный) минимум полиэкстремальной функции на отрезке a-b, то ничего, кроме метода перебора, здесь не применить. Желательно при этом делить отрезок неопределенности не на равные доли, а случайно, реализуя метод случайного поиска (рис. 6.56):

Поиск минимума функции методом случайного поиска

2. Один и тот же результат на компьютере можно получить разными путями. Но эти пути могут занимать разное время. Автор для оценки времени работы программ использует пользовательскую встроенную функцию GetTime(a). Эта функция возвращает время (в секундах), представляющее собой разницу между системным временем компьютера и значением аргумента функции GetTime[92]. Таким образом можно количественно оценить время выполнения отдельных Mathcad-операторов. С этой функцией можно проводить эксперименты и наметить некоторые пути оптимизации программ (темы лабораторных работ по программированию).

Замена произведения возведением в целую степень

На рис. 6.57-6.59 введутся простейшие действия: числа перемножаются – число возводится в n-ю степень; числа складываются – число умножается на целочисленную константу. Результаты, как и следует ожидать, одинаковые, но время их достижения разное.

Решение буквенной головоломки USA+USSR=PEACE (иллюстрация цикла с параметром)

Программа на рис. 6.6 решает буквенную головоломку USA+USSR=PEACE, где требуется указать, какие цифры скрываются за буквами. В программе три цикла с параметром (A, C и S), которые вложены друг в друга. В программе, не мудрствуя лукаво, можно было записать все семь циклов – по числу неизвестных задачи U, S, A, R, P, E и C. Но тогда перебор (а именно этим способом решается наша головоломка – вспомним «извращения» этюда 3) длился бы нестерпимо долго. Несложный предварительный анализ условий задачи (U ¬ 9, Р ¬ 1, Е ¬ 0 и R ¬ 10 + A) сокращает число циклов до трех и делает время счета приемлемым. Один из основных недостатков языка Mathcad – это невозможность вывода на дисплей промежуточных результатов расчета. А они не только помогают отлаживать программы, но и в ряде случаев просто необходимы при поиске единственно правильного решения из множества возможных (см., например, программы на рис. 6. 34 и 35 с решением задачи о компьютерах). В Mathcad-программах допустима запись вариантов ответов (промежуточных результатов) в матрицу (в вектор), которую после выполнения программы можно просмотреть, что и сделано на рис. 6.6. При этом в матрицу M записываются не только значения числовых переменных, но и текстовые константы[13]
(“+”, “=” и др.), делающие ответ более читабельным. Правильный ответ хранится в первом столбце матрицы M. Вернее, в первой строке – матрица у нас транспонируется для большей компактности[14]. Остальные ответы неверны – там разным буквам соответствуют одинаковые числа.
Цикл с параметром в среде Mathcad более гибок, чем его аналоги в языках BASIC или Pascal. Вот еще варианты заголовков циклов с параметром в среде Mathcad, кроме тех, которые показаны на рис. 6.6 (там специально приведены разные варианты заголовков циклов):
for A Î V        (V – вектор)
for A Î 5, 4.7, 8.9, 7.3×10-5
for i Î i1.. i2.
Последний вариант примечателен тем, что переменные i1 и i2 могут принимать любые значения, и необязательно, чтобы i1 было меньше i2. В языках BASIC и Pascal разное соотношение между i1 и i2 требует различного синтаксиса заголовка цикла с параметром:

For i= i1 To i2 или For i=i2 To i1 Step -1                         (BASIC)
for i:=i1 to i2 do или for i:=i2 downto i1do                       (Pascal).
Кнопки  и  позволяют досрочно выходить из циклов while и for, а кнопка  – совсем из программы. О них разговор особый (см. раздел 6.7 данной книги). Сейчас же проведем такую аналогию.
Все структурные управляющие конструкции Mathcad можно усмотреть в простой житейской ситуации: потчевание гостей чаем и кофе. Хозяйка проверяет, нет ли на столе пустой чашки (булева переменная, управляющая циклом while), и наполняет ее (тело цикла) чаем или кофе (альтернатива). Добавление в чашку кусочков сахара – новый, вложенный цикл. При разливе чая чашка (стакан) может лопнуть, что прерывает цикл, из которого выходят в конец цикла (break – гости встают из-за стола и занимаются чем-то другим) или в начало цикла (continue – на столе меняется скатерть и чаепитие возобновляется). Третий сценарий: разбитая чашка так расстраивает хозяйку, что вечеринка досрочно заканчивается (return).
Ниже приведены другие примеры программ в среде Mathcad.
Общие замечания. Язык программирования Mathcad по своей идеологии очень похож на язык FRED интегрированного пакета Framework. Говорят, что один из «погорельцев» фирмы Ashton-Tate (разработчика Framework) перешел в фирму MathSoft и приложил руку к созданию языка программирования Mathcad. Внешне же своими вертикальными линиями, фиксирующими вложения конструкций программы и операторные блоки, пакет Mathcad напоминает алгоритмические конструкции книги А.П.Брудно «Программирование в содержательных обозначениях» (М.: Наука, 1968). В свое время я очень увлекался подобными линиями, втискивая программы в рамки структурных диаграмм (см. рис. 6.21, а также книгу «128 советов начинающему программисту». – М.: Энергоатомиздат, 1991). Вертикальные линии программ Mathcad более наглядны (особенно для обучения структурному программированию), чем просто операторные скобки (begin-end на языке Pascal, фигурные скобки языка С, оператор list() языка FRED, конец строки BASIC-программы, круглые скобки математических выражений и т.д.).
Говоря о структурном программировании, нельзя не отметить тот факт, что разработчики языка Mathcad отказались от метки и операторов условного и безусловного перехода к метке как инструмента реализации разветвленных алгоритмов. Для некоторого смягчения этой категоричной позиции и были введены операторы return, break и continue.

Хронометраж вложенных циклов

На рис. 6.60 с помощью Mathcad рассчитывается сумма номеров строк и столбцов. Вывод: при организации вложенного цикла необходимо «запихивать внутрь» циклы с большим числом параметров. Дело в том, что внешний цикл организуется всего лишь раз, а внутренний – по числу значений параметра внешнего. На организацию (активизацию) цикла нужно время – отсюда и экономия.
Примем оптимизации, использованный на рис. 6.60 можно назвать постановкой матрицы «на попа»: если считать, что во внешнем цикле перебираются столбцы, а во внутреннем – строки, то формируемая матрица должна «стоять торчком» – в ней 3 столбца и 100 000 строк, а не наоборот.
Существенно ускорить работу программ можно за счет чистки циклов: «Не откладывай на завтра то, что можно сделать сегодня (послезавтра) – не делай в цикле то, что можно сделать до (после) цикла!» Из циклов (да и вообще из программ) целесообразно убрать все комментарии (у нас это текстовые константы), поместив их, например, в голове программы (см. рис. 6.57) либо правее зоны программы. Если в цикле делается ссылка на элемент вектора или матрицы и эта ссылка в цикле не меняется, то лучше этот элемент массива скопировать в скаляр до входа в цикл. Тело циклов, особенно вложенных, – это главное поле оптимизации: любая экономия здесь отзывается сторицей.
4.Разбивка программы на отдельные подпрограммы повышает ее читабельность (см., например, рис. 6.36-6.40), но одновременно увеличивает время прогонки. Отсюда вывод: в отлаженной программе для ускорения ее работы можно ссылки на подпрограммы (функции) заменить на сами подпрограммы. Особый выигрыш во времени счета достигается в программах, где ссылаются на подпрограммы (функции), записанные в других Mathcad-документах, хранимых на диске (см., например, рис. 6.49).
5. Большие массивы данных можно записывать либо в виде объемных векторов и матриц (см., например, рис. 4.10 и 4.13 в этюде 4), либо в виде файлов на диске, данные из которых считываются операторами READ и READPRN. Выбор того или иного способа хранения данных влияет и на читабельность программы и на скорость ее выполнения. Отсюда вывод, который читатель сделает для себя сам. Автор же, заканчивая эту главу, должен признаться, что три вышеотмеченных приема оптимизации Mathcad программ и другие, подобные им– это «ловля блох». По-настоящему оптимизировать программу можно, отказавшись от написания ее средствами Mathcad, и перейдя к программированию на языках не интерпретирующего, а компилирующего класса. Но при этом закроется доступ к специфическим Mathcad-функциям и операторам.

[1] В восьмой версии Mathcad новых инструментов программирования не появилось.

[2] Они остались в последующих версиях для совместимости с более ранними версиями и для тех пользователей, кто к ним привык. Правда, в мастере функций Mathcad 8 (см. рис. 1.28) функции until уже нет.

[3] На рис. 6.1 элементы векторов а и b выведены для контроля правильности решения задачи, что нередко приходится делать в целях отладки

программ (см. также рис. 6.29 и 6.30, где след поиска отображен на графиках – двух- и трехмерном).

[4] Язык Mathcad, развиваясь в седьмой версии, стал все больше приобретать черты языка С. Здесь нет ничего удивительного, так как сам Mathcad писался на этом языке.

[5] VBA – Visul Basic for Applications.

[6] В Mathcad-программе поиска корня функции методом Ньютона (см. рис. 6.17) читатель может увидеть дифференциал в его общепринятом обозначении. Таким же образом в программы записываются интегралы, суммы, произведения и т.д.

[7] Первое выражение (Pascal) содержит явную синтаксическую ошибку, второе – нет, так как на языке BASIC – символ «=» означает не только присвоение, но и булеву операцию «эквивалентно». В среде языка С программист написал бы А = А == В + С, а на языке Pascal . А := А = В + С.

[8] В седьмой и восьмой версиях Mathcad оператор вывода числового значения «=» автоматически (SmarOperator) превратится в оператор присвоения «:=». Но это умолчание можно отменить.

[9] Цикл по-другому еще называют итерацией. Вот что написано в статье «Итерация» одной занимательной энциклопедии: «см. итерация».

[10] Для ускорения счета рекомендуется убирать из программ комментарии, хотя бы из тела цикла. Компилятору нужно время не только на выполнение оператора, но и на то, чтобы понять, что данный оператор выполнять не следует.

[11] Ключевые слова begin и end в среде языка Pascal отмечают начало и конец программных блоков.

[12] По TV крутятся рекламные ролики: «Нашим школам не хватает учебников. Наши детские дома требуют ремонта. Пожалуйста, заплатите налоги!» Здесь уместно будет добавить: «Пожалуйста, не воруйте бюджетные средства!»


[13] А мы знаем, что в среде Mathcad число и текст – это информация одного типа Variant. Поэтому их можно объединять в векторы и матрицы.

[14] Для этой же цели на одной строке программы мы записывали несколько операторов, разделяя их пробелами. Пробел ставится так. Сначала операторы разделяются запятыми (так было возможно разделять операторы в седьмой версии Mathcad), а потом запятые стираются. При этом появляются круглые скобки, которые можно оставить, а можно убрать. Размещение нескольких операторов на одной программной строке, как и комментирование программ текстовыми константами – это недокументированные приемы, поэтому их по возможности лучше не применять (см. также рис. 6.26). Даже вне программ нужно стараться размещать операторы столбиком. Иначе пользователь Mathcad (особенно начинающий) часто будет сталкиваться с ошибкой размещения следующего оператора чуть-чуть выше предыдущего, что нарушает причинно-следственную связь.

[15] Такую задачу в свое время успешно решал на языке BASIC К.Лапинг (рубрика «Человек и компьютер» журнала «Наука и жизнь»), которую автор в свое время редактировал вместе с Ю.В.Пухначевым.

[16] В период между Рождеством и Крещением. Программа на рис. 6.9 написана автором (вернее, подправлена для Mathcad 8) 11 января 1998 года. Так что здесь все в порядке.

[17] Здесь более уместен цикл с постпроверкой, но его нет в среде Mathcad.

[18] До Mathcad 7 Pro их тип был вещественный и при необходимости комплексный. В седьмой и восьмой версиях тип переменных – Variant (помесь числа с текстом), если исходить из стандарта языка Visual Basic и технологии OLE.

[19] Слово Pro (professional) фигурирует в названии самой современной версии Mathcad – Mathcad 8 Pro. Но в нашем контексте (см. выше) оно является латинским словом «за». Хотя слово Pro в названии пакета можно считать и некой агитацией в пользу Mathcad.

[20] Такое было возможно в ранних версиях языка BASIC, где допускались длинные переменные, но они идентифицировались только по двум первым символам.


[21] Некоторые полагают, что лет через 10-20 мы перейдем к написанию русских текстов латиницей: sejchas tak pishut teksty mejdunarodnych telegram. Молдавия, Азербайджан и некоторые другие страны СНГ уже перешли от кириллицы к латинице. Основная причина в сфере информатики. Вспомним, какие абракадабры нередко приходят к нам по e-mail.

[22] У алхимиков есть символ: «Змея, глотающая свой хвост», который подходит и для рекурсии – маленькая программа, заглатывающая память компьютера.

[23] Автор зкладывает в книгу ошибку 2000-го года: если описанному правилу будет следовать читатель в 2001 году, например, то он неверно вычислит значение данной константы – 2.719.

[24] Кстати говоря, факториал отрицательных чисел не такая уж полная чушь. У факториала (оператор целочисленного неотрицательного операнда) есть вещественный «родственник» – гамма-функция (она есть в среде Mathcad), которая работает и с отрицательными нецелыми аргументами. Значение гамма-функции при целых отрицательных значениях «улетают» в плюс-минус бесконечность.

[25] Тема чисел Фибоначчи неисчерпаема. В США даже издается специальный журнал «Fibonacci Quarterly» (электронная версия: http://www.math.uga.edu/~andrew/Fibonacci/fibauthor.html).

[26] Тройки и семерки, как автор уже отмечал неоднократно, пронизывают Mathcad.

[27] Увлекающимся числовыми последовательностями можно рекомендовать через Internet зайти на сайт www.research.att.com/~njas/sequences и воспользоваться функцией lookup. После этого можно вводить фрагмент любой взбредшей в голову числовой последовательности и ждать ответа – вариантов продолжения этой последовательности, правда, только односторонних.

[28] Еще один «долгожитель», иллюстрирующий рекурсию в книгах по программированию.

[29] Подобные задания получают студенты автора, желающие досрочно сдать экзамен по «Информатике».

[30] Слегка косят две наши милые современницы – актрисы Татьяна Шмыга и Людмила Максакова.

[31] Который, например, что-то «позаимствовал» у другого программиста, но не признается в этом даже в суде.


[32] Если единицы физических величин не используются, то нужно их совсем отключить (окно Unit System, вызываемое командой Options в меню Math).

[33] У слова «догма» есть не только отрицательный, но и положительный оттенок. Без догм не обойтись в процессе воспитания и обучения.

[34] Можно использовать и другой критерий завершения цикла: значение анализируемой функции становится меньше значения заданной точности. Так было сделано в документе на рис. 6.1 и так задумано в стандартной функции root (см. рис. 3.1).

[35] В программу на рис. 6.18 вместо «безоперандного» оператора break можно вставить оператор return, что позволит убрать последнюю строку программы с указанием локальной переменной, чье значение программой возвращается. Хотя переменную можно убрать и в программе на рис. 6.18 с оператором break. Но есть хорошее правило, не полагаясь на умолчание (программа Mathcad всегда возвращает значение последнего присваивания), дополнительно фиксировать имя возвращаемой переменной (сравните окончания программ на рис 6.17 и 6.18).

[36] Программистам-ортодоксам, раз и навсегда исключившим метку из своего арсенала, можно посоветовать наложить на себя еще одну епитимью – писать программы без использования оператора if, опираясь только на цикл while и помня, что альтернатива с одним плечом – это цикл, тело которого выполняется либо раз, либо ни разу. Предлагаем читателю для начала исключить оператор if из программ этой книги. Пример – рис. 6.20 и 6.21.

[37] Многие программисты причисляют к основным структурным управляющим конструкциям и вызов функции, особенно, рекурсивный: числа Фибоначчи без рекурсии подсчитать можно (рис. 6.11), а числа Аккермана (рис. 6.13) – затруднительно.

[38] Метод последовательных приближений широко используется в инженерных расчетах. Если блок операторов, по которым рассчитывается новое приближение, объемный, то можно рекомендовать «опустить» оператор задания первого (предыдущего) приближения к оператору вывода значения очередного приближения, записав там Ответ?50 (если говорить о программе на рис. 5.22). Это исключит «ползанье» по Mathcad-документу.


[39] Структурная революция началась со статьи Э. Дейкстры «Programming without GOTO». Сейчас многие программисты-снобы, как нами уже отмечено, хвастают тем, что они написали не одну сотню программ, ни разу не обратившись к метке.

[40] В языке Visual Basic оператора Print тоже нет, а есть метод Print.

[41] Программы на рис. 6.26 и 6.27 были написаны для Mathcad 7, где не было средств оптимизации.

[42] Предполагается, что анализируемая функция y(x) на отрезке a-b непрерывна и имеет один минимум – представим себе веревку, протянутую между двух столбов. Оптимизация такой функции – типичная инженерная задача. Пример: самолет имеет минимальную (взлет и посадка) и максимальную скорость полета (рывок перехватчика); между ними «провисает» крейсерская скорость с минимальным расходом горючего на километр пути.

[43] Вернее, возвращает среднее арифметическое от a и b, когда отрезок между ними становится меньше TOL и одновременно накрывает точку минимума.

[44] Их четыре в двухмерной задаче, 6 в трехмерной и т.д.

[45] Первоапрельский выпуск (1997 г.) еженедельника «КомпьюТерра», который назывался «КомпьюМорра».

[46] Здесь записано ORIGIN, а не просто 0 (нуль) для того, чтобы не быть привязанным к текущему значению системной переменной ORIGIN.

[47] Попытка продлить шутку.

[48] Если иметь в виду плановое хозяйство, то «выделено».

[49] Подобные задачи мы решали в этюде 3.

[50] Хорошее правило: никогда не оставляйте в теле цикла с параметром один оператор, дополняйте его хотя бы комментарием, чтобы зафиксировать начало и конец блока операторов, составляющих тело цикла.

[51] Автор оставлял на работе включенный компьютер на выходные, а в понедельник утром считывал результат прогонки модели при N:= 1000000.

[52] Смотри ссылку в конце рис. 6.38; кроме того, эта задача есть в сборнике задач по программированию для школьников.

[53] Вариант для дам: дуэлянты стреляют не пулями, а шариками с краской. Есть такая игра под названием Paintball («красящий шарик») – участники носятся друг за другом со специальными пистолетами, оставляющими яркие пятна на одежде соперника.


[54] Многие исследователи сетуют на то, что компьютер, обрабатывая эксперимент, отдаляет (и даже отделяет) их от объекта исследования.

[55] Причин, почему у современных медицинских термометров на жидкокристаллический дисплей по-прежнему выводятся не слова, а числа, несколько. Главная, по-видимому, в том, что цифры во все времена были и будут вне языкового Вавилона прошлого и современного мира (информационное эсперанто) – они понятны и европейцу, и китайцу, и арабу независимо от их образовательного уровня. Но тот же европеец, китаец или араб, глядя на термометр, видит не цифры, а диапазоны: нормальная, повышенная и т.д.

[56] Пример нечеткого множества, кочующий из одного учебника по ТНМ в другой.

[57] Эта «анафема» коснулась и Mathcad, в среде которого метки нет (см. выше).

[58] Узкое и длинное ведро будет при носке волочиться по земле, а широкое – задевать за ногу. Понятия «удобно» нет в классической математике, но в ТНМ оно узаконено.

[59] Норма – это тоже из области теории нечетких множеств. Кто-нибудь по-настоящему задумывался, почему нормальное распределение называется нормальным?

[60] Их при желании можно создать – см. этюд 3.

[61] Она похожа на перевернутое и слегка помятое пожарное ведро.

[62] Здесь учитывается удобство уже не потребителя, а производителя пожарных ведер – круглая заготовка раскраивается без обрезков.

[63] В конце аллеи участка, где расположена дача автора, стоит пожарный щит. После определения параметров оптимального пожарного ведра автор не поленился – взял в руки линейку и пошел обмерить реальное пожарное ведро на щите. Но ведро, как и все остальное (топор, лом, багор и пр.) оказалось нарисованным на щите (виртуальный пожарный щит – «отмазка» от пожарной инспекции – в каморке папы Карло висел подобный котелок над очагом).

[64] Автор не устает повторять своим студентам, что в реальной жизни есть два нечетких множества: множество вакантных мест на рынке труда и множество людей, ищущих работу. Говоря языком математики, можно сказать, что эти множества пересекаются, но отнюдь не совпадают. Цель образования, кроме, конечно, получения удовольствия (см. комментарии к рис. 6.9), – это процесс попадания в область пересечения данных множеств.


[65] В этюде 3 на рис. 3.6 мы нарисовали что-то подобное – черный круг точек, случайно и равномерно расположенных в квадрате. В квадрат можно было «кидать» точки по иному закону распределения, например по нормальному. Так можно визуализировать нечеткое множество.

[66] Эксперимент не совсем чист – женщинам приходится вынашивать, рожать и воспитывать детей, что, конечно, отвлекает от научного и художественного творчества.

[67] Более-менее «приличные» дамские романы («Сага о Форсайтах», «Анна Каренина» и др.) написаны, кстати, мужчинами – Джоном Голсуорси и Львом Толстым.

[68] В момент завершения работы над этой книгой в продаже появился «черный» лазерный диск «Mathcad 8 Pro с документацией на русском языке». Но это был двойной обман: а) на диске была, естественно, ворованная копия Mathcad и б) документацией оказалась отсканированная или украденная в издательстве мягкая копия книги В.П.Дьяконова по Mathcad 7.

[69] Говорят, что играть на фортепьяно очень просто. Достаточно нажимать нужную клавишу в нужное время. Мы это подчеркнули еще в этюде 3, когда обсуждали «художества» на компьютере. Гениальных же пианистов единицы потому, что Создатель не в силах обслужить всех играющих. Проблемы трудолюбия музыканта (программиста) мы касаться не будем, отсылая читателя к «Моцарту и Сальери» Пушкина, где эта тема разработана достаточно глубоко.

[70] В английском языке нет такой путаницы – там пишут Copyright – права на копирование. У нас же этот термин переводят неправильно – «авторские права».

[71] Здесь могут быть не потери, а прибыли. Тот же автор, написав новый труд, может получить за него гораздо больше, если он известен в читающем мире не в последнюю очередь и через нелегальные копии. Примеры: Булгаков, Высоцкий, Пастернак, Бродский… Последние двое вряд ли получили бы Нобелевские премии, если б их в свое время издали массовыми тиражами.

[72] О великий и могучий!.. В одном предложении семь аббревиатур, но иначе не скажешь.

[73] Можно дать голову на отсечение, что у писавших обличительные статьи на компьютере хоть одна из программ (DOS-Windows-Word или DOS-Лексикон) стоит нелегально. Многие милицейские отделения оборудованы компьютерами (документация, базы данных и т.д. и т.п.), но опять же можно дать что угодно на отсечение, что ни в одном отделении, включая и то, из которого был организован рейд на компьютерные рынки, вы не увидите коробок с легальными версиями программ. Милицейские чины часто по телевизору комментируют криминальную сводку. На втором плане, как правило, компьютер – тоже, мол, не лыком шиты. На экране – две голубые панели NC. Ворованные, кстати говоря.


[74] В магазине концерна « Белый ветер» на Никольской улице в Москве висит плакат: татуированная рука накрывает мышку компьютера, а сверху надпись: «Не воруй!» Автор прошелся по магазину и посмотрел цены на ноутбуки (специализация концерна). Так вот, если надбавка к цене составляет 20-30%, то ее называют торговой, а если 200-300%, то – бандитской. На Западе цена самого дорогого ноутбука 2500 долларов. Дороже может стоить только какой-нибудь спецзаказ с перламутровыми клавишами. Купить ноутбук за 5000 «косых» да еще и полное программное обеспечение к нему может только тот, чья рука изображена на плакате, смысл которого после экскурсии по магазину меняется.

[75] Упоминавшееся московское отделение знаменитой фирмы, с одной стороны, борется с пиратством, а с другой – его косвенно поощряет. Один коллега автора купил там для фирмы, где он «халтурит», легальную копию офисной системы за 2500 долл., хотя на лотках ее продают за 90 рублей. При установке программы понадобилась консультация. Звонят продавцу, а он отвечает, что перепоручил послепродажную поддержку программы другой фирме. Звонят туда. А там отвечают, что у них консультации платные – 60 долл. за вопрос. За такие деньги они консультируют, естественно, всех подряд, а не только легальных пользователей.

[76] Сексуальный аспект проблемы, если хотите.

[77] Аналогия здесь и в том, что и тот и другой мешают жене и мужу (программе и пользователю). Настоящим же пиратам все нипочем – и пояс верности, и электронный ключ ломаются довольно просто. Еще одна параллель: беспорядочный секс и нелегальное копирование программ – это главный путь распространения вирусов, человеческих и компьютерных.

[78] См. главку «Как автор продавал программы» в этюде 3.

[79] Автор познакомился с такой практикой, учась (хорошему и плохому) в Германии. Там нередко ставят программу одной установки на много машин, но одновременно просят на это разрешение фирмы-изготовителя. Фирма дает на это добро, идя навстречу университету (где еще можно так успешно рекламировать свою продукцию) и понимая, что в случае отказа программы все равно поставят.


[80] Как сказать. Этот этюд самый объемный в книге. К помощи Mathcad часто обращаются те, кто не может или не хочет работать с чистыми языками программирования. Но постепенно эти люди втягиваются в программирование в среде Mathcad и по необходимости переходят к «серьезным» языкам.

[81] Можно только предположить, что отладчик фирма MathSoft приберегает для «этапной» версии Mathcad – Mathcad 2000. Сейчас как из рога изобилия посыпятся программные продукты с приставкой «2000».

[82] Здесь мы отказались от обрамления отдельных операторов серым фоном.

[83] Принцип «Щелкни кобылку по носу – она махнет хвостом».

[84] Что с успехом делают студенты автора при курсовом и дипломном проектировании.

[85] С точки зрения чистой математики действительных значений даже в узком диапазоне неограниченное количество. В среде Mathcad и в других программных средах действительных значений переменных конечное число.

[86] У фанатов языка APL (у «апиэльщиков») есть неписаное правило – программа должна полностью умещаться на экране дисплея.

[87] Считается, что подпрограмма – это припев песни, который поют несколько раз, а в текстах песен печатают только один раз. Но отдельный элемент программы целесообразно выделить в отдельную процедуру даже в том случае, когда этот элемент работает всего лишь раз. Во-первых, так удобнее отлаживать программу, а во-вторых, эту процедуру можно вызывать из других программ.

[88] Автор при тестировании бета-версий Mathcad просил разработчиков ввести в систему жесткий запрет на переопределение встроенных функций и констант (встроенные операторы, кстати, переопределять нельзя), но это не было сделано.

[89] Из них можно сделать заставку для экрана дисплея, появляющуюся перед глазами пользователя, когда он на время задумывается и не касается клавиш компьютера.

[90] Водительское определение микросекунды: это время, прошедшее с момента появления зеленого света светофора до подачи звукового сигнала водителем, сидящим в задней машине. Микросекунда здесь не 10-6 с, а элемент нечеткого множества «очень быстро».

[91] Метод половинного деления – это универсальный метод численного решения задач. Вот его «зоологическая» интерпретация: «Как поймать льва в пустыне? Нужно ее оградить забором, перегородить пополам и посмотреть, где оказался лев. Эту половинку пустыни перегородить еще раз. Так поступать до тех пор, пока (оператор while) лев не окажется в ящике, размером TOL.»

[92] Эту функцию и описание ее создания можно «скачать» из ftp-сервера ftp:\\twt.mpei.ac.ru\ochkov\mathcad и поместить в подкаталог userefi каталога Mathcad. После этого ссылка на нее появится в окне вставки функций (рис. 1.28).

Программа-константа

Программу, формирующую константу, подобрать несложно. Но зачем? Константу можно раз и навсегда рассчитать (задать), а потом вставлять результат в Mathcad-документ (константы p, е и др.). Но иногда для лучшего понимания сути константы полезно оставить механизм ее формирования открытым. Программа на рис. 6.7 подсчитывает число, фигурирующее в легенде об изобретателе шахмат, который в награду попросил дать ему такое количество зерна, какое он может положить на шахматную доску с тем, чтобы на первой клетке было одно зернышко (21-1 т.е. 20), на второй – два (22-1), на третьей – четыре (23-1) и т.д. (на новой клетке зерен в два раза больше, чем на предыдущей). На рис. 6.7 подсчитывается не все количество зерен на шахматной доске, а их масса в британских тоннах, не превышающая 100 000 тонн (масса одного зерна принята за 0.3 грамма).
Программы-переменные и программы-функции читатель увидит ниже.

Программа-скаляр

Программа на рис. 6.8 возвращает скалярное значение – номер элементов (iopt) векторов X, Y и Z при котором... В этюде 3 мы искали домик на дачном участке, где следует устроить, например, продовольственный ларек. Критерий выбора – минимальная сумма расстояний от ларька до всех остальных домиков. Теперь (рис. 6.8) ларек у нас уже космический, а задача трехмерная. На рис. рис. 3.12 подобная задача решалась без привлечения инструментов программирования.
Программы на рис. 3.12 и 6.8 довольно примитивны. Но читатель может их развить, заменив, например, декартову систему координат на географическую, где вектор X будет хранить значения долготы, а вектор Y – широты
объектов. Тогда задача может свестись к поиску места, например, для вертолетной площадки, обслуживающей геологов или нефтяные скважины, и стать не только более сложной, но и более реальной[15].

Программа-матрица (пасьянс «Турецкий платок»)

Рассмотрим эту особенность на такой занимательной задаче.
Очень часто, решая ту или иную проблему, мы оказываемся в шкуре буриданова осла. Задача может иметь два альтернативных решения, как две охапки сена слева и справа от упомянутого животного. Все доводы «за» и «против» уравновешены. Как в этом случае поступить? Ехать или не ехать в командировку? Покупать или не покупать еще один винчестер? Поистине, гамлетовские вопросы задает нам жизнь!
Некоторые в таких ситуациях бросают монетку, другие загадывают мужчину или женщину и смотрят в окно, ожидая, кто первый появится. Но все это ненаучные методы. Монетка может куда-нибудь закатиться, а по улице как назло за целый час только кошка и пробежит...
Есть проверенный столетиями метод принятия подобных решений. Достаточно разложить пасьянс. Сошелся – решение принято и все сомнения прочь. Можно подыскать дополнительные доводы в его пользу, и начать воплощать в жизнь. Пасьянс психологически нас на это настраивает.
Но принять решение подобным образом иногда бывает трудно, так как не всегда под рукой есть колода карт, да и не совсем удобно раскладывать их на рабочем месте. Но это можно сделать и на экране дисплея. В среде Windows, например, есть игры-пасьянсы («Солитер» и «Косынка»), но мы придумаем что-нибудь новенькое, а, главное, более занимательное и поучительное – разложим в среде Mathcad старинный пасьянс «Турецкий платок». На это есть три причины:
1.Чтобы лучше освоить программную среду, нужно постараться решить в ней задачу, для этого крайне неподходящую. Да, это своего рода программистское извращение, но – см. этюд 3.
2.В детстве каждый нормальный человек, наигравшись, ломал игрушку, чтобы посмотреть, как она устроена. Посмотрим и мы, как тасуется колода и раскладывается пасьянс.
3.По традиции гадать на картах и раскладывать пасьянсы разрешается только в святки[16]. Наш пасьянс можно считать числовой головоломкой, которую позволительно решать круглый год.
Mathcad-документ (см. рис. 6.9) позволяет разложить пасьянс «Турецкий платок» по следующим правилам. Из одной перетасованной колоды в 52 листа выкладывают картинкой вверх пять рядов по 10 карт в каждом. Последние две карты кладут в шестой неполный ряд на любое место, как правило, к первому и второму столбцам. Требуется распустить этот «платок», снимая из разных столбцов за один ход по две нижние одинаковые карты – тройки, дамы, тузы и т.д.

Для снятия карт нужно скопировать правую часть оператора П = ... (саму матрицу) на свободное место, подвести курсор к нужной текстовой константе (к карте), щелкнуть по левой кнопке мыши и нажать клавишу Delete. Вместо числа появится пустой квадратик.

Из разложенного пасьянса сняты две двойки. Теперь можно снять две восьмерки, два короля или две десятки (вопрос – какие из трех открытых). После этого откроются новые карты. Если удастся снять все 52 карты, то это означает, что в командировку все-таки ехать придется, а винчестер покупать надо.

Составление программы, формирующей матрицу П (раскладка пасьянса) – прекрасное и, что не менее важно, занимательное средство изучения таких базовых понятий линейной алгебры, как вектор и матрица. Так, при формировании матрицы П транспонируется матрица Масть (она ставится «на попа» – матрица с одной строкой превращается в матрицу с одним столбцом, то есть в вектор). Далее с помощью функции stack составляется новая нерастасованная колода карт, где одна отсортированная масть идет за другой (вектор Колода). Затем в цикле с параметром (for...) с помощью цикла while[17] и функции rnd идет формирование перетасованной колоды – вектора Тасованная_колода, который в конце программы двойным циклом с двумя параметрами (for... for...) складывается слоями в матрицу П.

Программу, формирующую матрицу П, можно развить: заставить программу отбраковывать явно нерешаемые раскладки – такие, например, где в одном столбце оказались три или даже четыре одинаковые карты. Еще одна тупиковая ситуация – две пары карт крест накрест закрывают друг друга. Это будет хорошим упражнением, закрепляющим навыки работы с «матричными» операторами и функциями в среде Mathcad. А вот более сложное задание читателю: доработать программу так, чтобы она сама раскладывала пасьянс, либо на худой конец сообщала, что его можно решить, просто снимая снизу первые подвернувшиеся одинаковые открытые карты. Более умная стратегия подразумевает выбор карты из трех или четырех одинаковых открытых карт.


Кроме линейной алгебры, наша программа затрагивает и другие интересные разделы математики – теорию вероятностей, статистику (см. функцию rnd, генерирующую псевдослучайные числа). Интересный вопрос: можно ли составить программу, высчитывающую вероятность сходимости того или иного пасьянса? Считается, что пасьянс «Солитер», входящий в стандартную поставку Windows, раскладывается при любых начальных раскладках. Но это только гипотеза…

Часто бывает так, что человек прекрасно делает то, чему он учился играючи и с большим удовольствием: ходит, говорит, плавает, катается на велосипеде и т.д. и т.п. Автор, например, задолго до школы научился считать, играя в карты: валет – двойка, дама – тройка и т.д. И сейчас, обращаясь к своим студентам, не устает повторять, что главное, что нужно получать от учебы, – это не знания, не практические навыки, а... удовольствие. Не получая радости от учебы, от повседневного труда, человек тратит свою жизнь впустую... Например, если тяжело идет освоение линейной алгебры – расслабьтесь и постарайтесь получить удовольствие.

Начинать изучение векторов и матриц (массивов данных) в курсе программирования (информатики) можно со знакомства со встроенными функциями и операторами конкретной программной среды. А можно раскладывать пасьянсы.

Как уже отмечалось ранее, переменные в Mathcad могут быть локальными, самообъявляющимися в программах (как, например, переменные Случайное_число, Колода, Карта, Столбец и Ряд в программе на рис. 6.9). Значение локальных переменных пропадает по выходу из программы. Разработчики языка Mathcad посчитали лишним обязательное объявление переменных до их использования (как это делается при работе с языком Pascal, например). Наверное, переменные не объявляются из-за того, что они все однотипные[18]. Но необъявление переменных может приводить к ошибкам, которые трудно выявить, так как язык Mathcad не имеет средств отладки

(debugging). Ввел программист в программу переменную dаy, а через пару операторов написал dey (что по произношению более соответствует английскому слову day (день); можно умудриться написать и dаy, где вторая буква будет из русского алфавита) – программа выдает неверный ответ. Опечатки в программе часто бывают намного страшней в плане отладки, чем ошибки алгоритма. Кроме локальных и глобальных переменных, значения которых заданы вне программы и автоматически в нее проникают, в среде Mathcad есть и системные (предопределенные) переменные и константы. Пример – числа e и p, значение которых определено самой системой (математикой), а не пользователем (см. приложение 4).


Мы уже не первый раз используем буквы кириллицы в именах переменных и функций. В программе на рис. 6.9 впервые все переменные прописаны по-русски. Pro и Contra этого приема.

Pro[19]:

Полные имена переменных (Столбец, Ряд вместо i, j) делают программу более простой для понимания, но более сложной для написания (рекомендуется длинные переменные писать один раз, а потом копировать в нужных местах). Конечно, можно было написать и английские термины в качестве имен переменных, но они будут выглядеть чужеродными в пасьянсе, программу которого для русскоязычного читателя написал человек, считающий себя русским. Да и автор, честно говоря, не знает, как будет по-английски «Масть», «Колода». Лезть же в словарь не с руки. Проще написать Мast, Коloda. Проще, да некрасиво (см. ниже).

Contra:

Русские имена переменных порождают «смешенье языков французского с нижегородским»: for Столбец?! Правильнее и грамотней писать for Солбца[20] (для Столбца); на многих программистов русское имя объекта программирования (файла, переменной, функции и т.д.) действует как красная тряпка на быка[21].

В латинском и русском алфавитах многие буквы (например, а, с) совпадают по написанию. Из-за этого в программе могут оказаться переменные, одинаковые для человека, но разные для Mathcad.

Выбор для переменных шрифта с окончанием Cyr приводит к перекодировке символов. Из-за этого, например, может пропасть восклицательный знак в факториале и др.

Команды символьных преобразований

Семь комментариев к примерам на рис. 7.1:
1. При символьном вычислении неопределенного интеграла (пункт 1 на рис. 7.1) и при интегрировании выражения константы опускаются (полагаются равными нулю). Отсюда такой «парадокс»: пользователь взял производную синуса в квадрате (см. рис. 7.2), а от полученного выражения ¾ первообразную. По идее должен вернуться прежний синус в квадрате, но мы получаем косинус в квадрате да еще и с минусом. Удивляться здесь можно, только если забыть тригонометрическую форму записи теоремы Пифагора (sin(x)2+cos(x)2=1) и тот факт, что при интегрировании константа принимается равной нулю.

Панели работы с операторами символьных преобразований

Сам оператор символьных преобразований вводится в Mathcad-документ нажатием кнопки g ® на панели Evaluation или Symbolic. После этого на экране дисплея появляется такая заготовка: g g ®. Первый операнд данного оператора – это какая-либо алгебраическая конструкция (выражение, неравенство, уравнение и др.), а второй – ключевое слово, задающее направление символьного преобразования[20]: упростить, решить, факторизировать, вычислить коэффициенты полинома и т.д. Оператор символьного преобразования с ключевым словом существенно богаче по своим возможностям команд меню Symbolic. Поэтому, как было отмечено выше, это меню фактически лишнее. Кроме того, оператор символьного преобразования сразу выдает новый ответ, если в исходном выражении что-то поменяли. Здесь не нужно стирать старый ответ, как это требуется при обращении к командам меню Symbolic.
Само ключевое слово оператора g g ® (второй его операнд) может иметь новый ключ, определяющий детали символьного преобразования. Только две команды (Simplify – Упростить[21]
и Complex – представить в комплексном виде) не имеют дополнительных ключей. Чтобы в них не запутаться, лучше не выводить на экран заготовку оператора g g ®, а поступать по-другому: записать или откуда-то скопировать исходное выражение (a+b×x=0, например) и нажать на кнопку с названием соответствующего преобразования (solve, например). После этого на экране появится уже не заготовка оператора решения уравнения, а его, так сказать, полуфабрикат: a+b×x=0 solve, g ®. В черный квадратик достаточно вставить имя переменной, по которой решается уравнение, чтобы получить ответ: -b/a. Здесь можно оперировать не только переменной, но и новым выражением – x- 1, например:

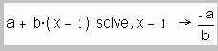
Особо хочется отметить оператор разложения на множители g factor, g ®. Если его применить не к алгебраическому выражению, а к числу натурального ряда, убрав при этом его ключ (g factor ®), то он будет называться Разложить на простые множители. Простые числа – это такие числа, которые делятся без остатка либо сами на себя (результат – единица), либо на единицу (результат – само простое число). Простые числа (2[22] – единственное четное простое число, 3, 5, 7, 11, 13, 17, 19, 23 и т.д. до бесконечности) – простые и по названию, и по определению, но за ними стоит много проблем теоретического и практического плана, одна из которых такая...

Сэм, Билл и Джон договорились... Нет, не сразиться на дуэли (см. этюд 6), а обмениваться друг с другом шифрованными сообщениями по таким правилам:

каждый i-й участник придумывает свой шифрующий (ШАi) и дешифрующий (ДШАi) алгоритмы;

шифрующие алгоритмы открыты, они известны всем участникам;

свои дешифрующие алгоритмы каждый участник держит в секрете;

если i-й участник захочет послать шифрованное сообщение j-му участнику, то он использует ШАj (он, как мы договорились, известен всем);

j-й участник, получив сообщение от i-го участника, использует ДШАj, который, как мы знаем, известен только j-му участнику;

i-й участник может послать j-му участнику шифрованное сообщение с электронной подписью[23]; для этого i-й участник, посылая сообщение j-му участнику, использует цепочку шифров ДШАi-ШАj. Получив сообщение, j-й участник читает его так: ДШАj-ШАi, восстанавливая исходный текст. При этом j-й участник будет знать, что только i-й участник мог послать такой дважды зашифрованный текст, так как при шифровании был использован ДШАi, известный только i-му участнику.

Все это выглядит просто и красиво. Проблема заключается в разработке шифрующих и дешифрующих алгоритмов. Поступим для начала так. Пусть все участники переводят свое сообщение из текста в число N (“АББА” – 01020201, например). Затем по шифрующему алгоритму Сэм возводит число в квадрат, Билл – в куб, а Джон – в четвертую степень (ША1:=N2; ША2:=N3; ША3:=N4). Дешифрующие алгоритмы (их участники должны держать в секрете) сводятся к извлечению квадратного корня, кубического корня и корня четвертой степени соответственно и в переводе полученного числа в текст. Но такая тайна будет тайной Полишинеля, так как криптоаналитику ничего не стоит, просмотрев несколько сообщений, раскрыть не только шифрующий алгоритм (а из этого никто особой тайны не делает), но и дешифрующий. Проблема создания надежных функций-ловушек

(функций, обратный алгоритм которых невозможно раскрыть, сколько ни анализируй прямой алгоритм), до сих пор полностью не решена. В криптографии пока довольствуются функциями-ловушками с «потайной кнопкой», расположение которой известно только владельцу шифра. Прятать такую кнопку можно с помощью простых чисел.

Дело в том, что сгенерировать простое число можно довольно быстро. Тем более (тем быстрее) на компьютере. Но если два довольно больших простых числа перемножить и попросить компьютер по произведению найти исходные сомножители, то эта задача окажется неразрешимой, вернее, для ее решения потребуются «миллионы лет работы самого современного компьютера»[24].

Итак, участники «шифровальной дуэли» разрабатывают шифрующие алгоритмы, используя простые числа так, что посторонний, анализируя послания, может узнать только произведение (составное число). Проблема раскрытия дешифрующего алгоритма сводится к нахождению сомножителей – к разложению числа на простые множители.

Разложение чисел на простые множители

На рис. 7.11 даны примеры работы оператора n factor ®. Если исходное число n простое, то система Mathcad довольно быстро (секунды, минуты) доказывает это и выдает один сомножитель – само исходное простое число. Короткие составные числа раскладываются на простые сомножители также за приемлемое время. Но если составное число удлинить, то Mathcad «задумывается» намертво. Не «зависает», а именно задумывается. Автор оставлял включенную машину на выходные: вместо курсора-стрелки появлялся курсор – докторская четырехуголка, что свидетельствовало о работе символьного процессора. В понедельник ответа не было, а после нажатия клавиши Esc, вызывающего диалоговое окно прерывания вычислительного процесса, и щелчку по кнопке OK работоспособность Mathcad восстанавливалась: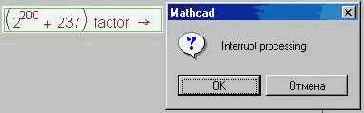

Простые числа на рис. 7.11 – это не просто простые числа, взятые наугад, а числа из различных литературных источников, где они отмечались как самые большие простые числа, известные человеку на определенных этапах развития математической науки и техники счета. Числа вида 2n-1 называют числами Мерсенна (http://www.mersenne.org). Они могут быть простыми лишь в том случае, если n – простое число (условие необходимое, но недостаточное – число 267-1 составное, хотя число 67 простое). До сих пор не доказано, имеется ли конечное или бесконечное число простых чисел Мерсенна[25]. То же можно сказать и в отношении простых чисел, состоящих только из единиц.
Особо хочется отметить число 2521-1. На рис. 7.11 показано, что это число Мерсенна – простое. Но в книге Мартина Гарднера (о ней ниже), сказано, что в 1982 году суперкомпьютер[26] «Крей» разложил его на три простых множителя за 32 часа работы. Где здесь ошибка? Либо Mathcad неправильно факторизирует числа, либо в книге Гарднера прошла опечатка (очепятка). Второе вероятнее, так как в книге отмечено, что это 69-значное число, тогда как на самом деле оно имеет больше знаков. Предлагаем читателю самому разобраться в этом вопросе. Автору тут важно поднять проблему и наметить пути ее решения с помощью Mathcad.

Для проверки чисел на простоту используют так называемую малую теорему Ферма[27] (см. пункт 2 на рис. 7.11). Если p – простое число, а число a – случайное, меньшее, чем p, то функция Ferma возвращает единицу. Если р – составное число, то функция Ferma возвращает число, большее единицы. И большая и малая теоремы Ферма пока считаются не доказанными, но если кандидат на простое число несколько раз выдерживает тест Ферма[28], то его считают «условно» простым и используют в шифровальном деле.

Я только что изложил главу «Надежные шрифты» из книги Мартина Гарднера «От мозаик Пенроуза к надежным шрифтам» (М.: Мир, 1993). После ее прочтения у меня возникло такое чувство, что либо я сам что-то недопонимаю, либо и меня и Гарднера кто-то искусно водит за нос, отвлекая от раскрытия настоящих алгоритмов шифрования.

Вот отрывок из этой книги.

«Объясняя, как работает их (шифровальная. – здесь и далее примечания автора) система, авторы из МТИ (Массачусетский технологический институт) выбрали в качестве исходного текста парафраз ремарки из «Юлия Цезаря» Шекспира (акт I, сцена 2): "ITS ALL GREEK ТО ME" («Для меня все это сущая тарабарщина» – мы говорим «китайская грамота», англичане же при этом вспоминают греков).

Прежде всего, этот текст преобразуется в одно большое число с помощью стандартного ключа: А=01, В=02, ..., Z=26 (00 – пробел между словами). Получается число 09201900011212000718050511002015001305.

Полученное число шифруется путем возведения его в s-ю степень по модулю некоторого составного числа r. Составное число r получается как произведение двух случайно выбранных простых чисел p и q, каждое из которых не менее чем 40-значно. Число s должно быть взаимно простым с числом p-1 и q-1. Числа s и r общедоступны: они используются в шифрующем алгоритме. Операция шифрования осуществляется весьма эффективно даже при очень больших значениях r; на практике она требует менее одной секунды компьютерного времени.

Два простых множителя числа r хранятся в памяти компьютера, поскольку они используются в секретном обратном алгоритме. Обратный алгоритм, используемый при дешифровке, состоит в возведении числа-шифротекста в другую степень t и в нахождении остатка от деления полученного числа на r, то есть в приведении по модулю r. Как и в предыдущем случае, на это уходит менее секунды машинного времени. Но показатель t может вычислить только тот, кто знает p и q ¾ два простых числа, которые хранятся в секрете.


Если исходный текст слишком велик для того, чтобы с ним можно было обращаться как с одним числом, то его следует разбить на блоки и каждый блок рассматривать как отдельное число. Я не буду вдаваться здесь в дальнейшие подробности. Они носят несколько технический характер и ясно изложены в отчете МТИ.

Для шифрования текста ITS ALL GREEK TO ME группа из МТИ выбрала s=9007 и r=114381625757888867669235779976146612010218296721242362562561842935706935245733897830597123563958705058989075147599290026879543541.

Число r есть произведение 64-значного простого числа p и 65-значного простого числа q, каждое из которых выбрано случайным образом. Шифрующий алгоритм заменяет число, соответствующее исходному тексту (09201...), следующим числом-шифротекстом: 199935131497805100452 31712274026064742320401705839146310370371740625971608948 927504399209626725826750128935544613538 23769748026.

Желая поощрить тех читателей журнала «Scientific American[29]», которые хотели бы испробовать свои силы на поприще криптоанализа, группа из МТИ зашифровала с помощью того же общедоступного алгоритма другой текст. Шифротекст вы видите на рис. 92 (см. книгу Гарднера). Его оригинал представляет собой предложение на английском языке. Сначала оригинальный текст был превращен в число с помощью стандартного метода, который был объяснен выше, полученное число возведено в 9007-ю степень (по модулю r) с помощью остроумного метода, изложенного в отчете. Тому, кто первым расшифрует текст, группа из МТИ обещала выплатить премию в 100 долларов.

Для доказательства того, что шифротекст действительно исходит от группы из МТИ, к нему была добавлена следующая подпись: 16717861150380844246015271389168398245436901032358311217835038446929062655448792237114490509578608 655662496577974840004057020373.

Подпись зашифрована с помощью секретного обратного шифрующего алгоритма. Так как читатель не располагает своим общедоступным шифрующим алгоритмом, вторая шифрующая операция была опущена. Каждый читатель, имеющий доступ к компьютеру и алгоритмам, опубликованным в отчете МТИ, может легко прочитать подпись с помощью общедоступных шифрующих алгоритмов группы МТИ, то есть возвести приведенное выше число в 9007-ю степень и перейти к остатку от деления на r.


Проделав эти операции, читатель получит число 06091819200019151222051800230914190015140500082114041805040004151212011819. Пользуясь стандартным ключом, читатель расшифровывает это число как FIRST SOLVER WINS ONE HUNDRED DOLLARS («первый, кто расшифрует текст, получит сто долларов»). Этот подписанный шифротекст мог быть получен только от группы из МТИ, так как обратный алгоритм, которым был зашифрован исходный текст, известен только членам этой группы.»

На этом заканчивается отрывок из книги Гарднера. Он сначала писался Гарднером по-английски, затем набирался в типографии, потом переводился на русский язык, опять набирался в типографии, затем сканировался автором для вставки в данную книгу. При такой технологии ошибки в числах текста очень вероятны. Тут вспоминается старая карикатура. Человек с перевязанными руками и ногами лежит на больничной койке, а диктор по телевизору, поставленному в палате, говорит: «Приносим извинения! В нашу вчерашнюю передачу «Делай с нами, делай как мы, делай лучше нас!» вкралась ошибка». Римейк карикатуры. «Пациент «палаты № 6» в книге по компьютерной математике читает приписку: «В наше предыдущее издание вкралась ошибка».

Автор перемножил в среде Mathcad[30]

два простых числа и поместил произведение в пункте 3 на рис. 7.1. Кто первым определит, что за простые числа были перемножены (найдет потайную кнопку шифра), получит приз, название которого также зашифровано: «Кмапвсптор к мвуепа»[31].

Оператор символьного преобразования с ключевым словом можно считать зачатком нового языка программирования, ориентированного не на вычислительный, а на аналитический процесс. Но интеграция символьной математики в среду Mathcad еще слаба и требует обилия ручной работы, без которой не составить даже функции пользователя из преобразованного выражения.

Один из коллег автора пришел в полный восторг, увидев действие пары expand – series. Ему (а он преподаватель математики в институте) по долгу службы приходится составлять вопросы для вступительных экзаменов. Ключевые слова expand – series позволяют как из рога изобилия сыпать вопросами с заголовком «Упростить», заранее имея правильный ответ. Несколько охладила этот восторг мысль о том, что абитуриенты пронесут

на экзамен ноутбук[32]

и ключевыми словами factor и simplify все эти примеры «разъяснят». Правда, на экзамене, как и в самом учебном процессе, требуется не столько ответ, сколько промежуточные выкладки... К проблеме щита и меча во взаимоотношениях ученика и учителя мы вернемся чуть позже, рассматривая место пакета Mathcad и ему подобных в процессе преподавания не только чисто технических дисциплин, но и самой высшей математики.

В среде Mathcad 8 можно вести цепочку символьных преобразований, показывая или не показывая промежуточные выкладки, которые иногда бывают настолько громоздкими, что их не то что рассмотреть – стереть с экрана бывает затруднительно.

Решение задачи о балке средствами символьной математики

На рис. 7.12 показано, как оператор solve с решает нашу старую задачу о раскрое коробки (коробок) максимальной вместимости: берется квадратная заготовка, по углам которой вырезаются маленькие квадратики. Полученная таким образом крестовина складывается в коробку (см. схему на рис. 2.4 в этюде 2). Найти параметры раскроя, дающие максимальный объем коробки. В этюде 2 мы развили эту известную школьную задачу, отметив, что из обрезков можно делать новые коробки, которых в принципе может быть бесконечное множество.
Комментарии к рис. 7.12:

В пунктах 1 (одна коробка) символьные преобразования ведутся «цугом» с выводом промежуточных аналитических выражений. Такая цепочка операторов получается следующим образом: записывается оператор дифференцирования (см. пункт 1) и нажимается кнопка оператора символьного преобразования «®» в панели Simbolic:



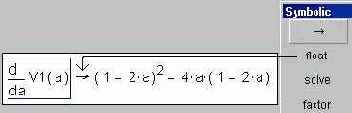
Далее ответ (производная от функции V1) охватывается курсором и нажимается кнопка Simplify в той же панели инструментов:



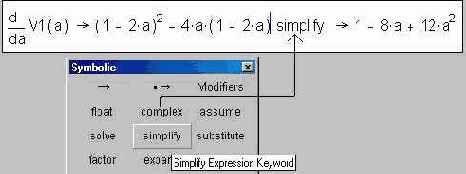
Затем к упрощенной производной прикладывается оператор решения уравнения (solve, a), возвращающий два корня, первый из которых (1/6) – ответ по задаче о коробке.

В пункте 2.1 (бесконечное число коробок с постоянной пропорцией раскроя a) символьные преобразования также ведутся «цугом». Одно из неудобств такой технологии в том, что промежуточные результаты выстраиваются по горизонтали и из-за этого их неудобно рассматривать на экране дисплея и распечатывать на бумаге принтера. На рис. 7.12 (а это, как читатель знает, «заморозка» экрана дисплея, доработанная в среде графического редактора) промежуточные выражения выстроены по вертикали, где стрелки показывают последовательность преобразований. Аналитический ответ (а численного здесь получить нельзя из-за того, что суммируется бесконечный ряд) – это вектор уже с четырьмя элементами, последний из которых (0.1736…) – решение задачи. Здесь дополнительно задействован оператор float, n, возвращающий число с плавающей точкой с n[33] знаками[34].

В пункте 2.2 операторы, решающие задачу о бесконечном числе коробок, выстроены не «цугом», а «парой», если так можно выразиться. При этом промежуточные результаты не показываются, так как они очень громоздки, и ничего не дают ни уму ни сердцу. Обычно пользователь комбинирует «упряжку» символьных преобразований, получая какое-то подобие «шестерни», когда лошади идут парами цугом.

В решении двухмерной оптимизационной задачи о пяти коробках (пункт 3 – два шага раскроя) выведены и аналитические и численные ответы (их четыре; правильный – второй).

В решении трехмерной оптимизационной задачи о двадцати одной коробке (1+4+16 –пункт 4) выведены только численные ответы (их двенадцать; правильный – восьмой сверху). Честно говоря, задача о любом числе коробок сводится к одномерной оптимизации последовательными решениями: пропорция последнего раскроя равна 1/6; зная это, можно одномерной оптимизацией найти раскрой первого шага из двух при пяти коробках и т.д. Здесь просматривается рекурсия, к которой мы еще вернемся в конце этюда.

Из рис. 7.12 видно, что символьный процессор пакета Mathcad выдает много лишних ответов. Из-за этого не только увеличивается объем Mathcad-документа, но и неизбежны сбои, когда символьная математика отказывается выполнять простейшие, на взгляд человека, операции или выполняет их не так как надо. В связи с этим в среду Mathcad введены операторы и ключи, позволяющие игнорировать (по-английски to assume) некоторые направления преобразований. На рис. 7.13 даны примеры таких игнорирований. Во-первых, пустой с точки зрения вычислительной математики оператор присваивания x:=x (пример 1 на рис. 7.13) лишает переменную x (или какую-то другую) ее численного значения. В примере 2 упрощается квадратный корень из икса в квадрате. Результат получается разным в зависимости от типа переменной x.

Игнорирования при символьных преобразованиях

По умолчанию тип всех переменных, участвующих в символьных преобразованиях, – комплексное число. Отсюда и соответствующее «упрощение» квадратного корня из квадрата – scgn(x)×x. Можно игнорировать отрицательные значения переменной (assume, x³0) и получить на самом деле упрощенный ответ – x. Ключ assume=real заставляет рассматривать все переменные в качестве вещественных (реальных). При этом можно оговорить диапазон изменения значений вещественных переменных – ключ assume=RealRange(0,¥). Ключ trig заставляет в тригонометрических преобразованиях учитывать тождество sin(x)2+cos(x)2=1.

Задача маленького Гаусса

Пакет Mathcad с выключенным режимом оптимизации (умолчание), столкнувшись с суммированием, начнет по примеру нормальных (талант – это аномалия) одноклассников Гаусса прибавлять к единице двойку и т.д.: 1+2+3+4+5+...+100. В среде Mathcad мы тоже можем написать такое длинное выражение, но проще воспользоваться оператором суммирования – см. рис. 7.14. Если в примере на рис. 7.14 увеличить значение n до миллиона, например, то время счета станет неприемлемо долгим. Если это не суммирование, а интегрирование (в руководстве пользователя Mathcad приведен пример с тройным интегралом), то это сути дела не меняет: пакет Mathcad будет по-прежнему что-то там долго и упорно суммировать[36], опираясь на соответствующий численный метод (прямоугольников, трапеций, парабол и т.д.[37]). Такие расчеты можно и нужно оптимизировать. В конце рис. 7.14 получена простая формула, которой можно заменить сумму членов натурального ряда: (n2+n)/2. Если включить режим оптимизации (переключателем Optimize в меню Math –см. рис. 7.14), то пакет Mathcad будет пытаться во всех выражениях искать упрощающие формулы и работать уже с ними, а не с исходными выражениями. Это будет глобальная оптимизация. Возможна и «точечная», локальная оптимизация, когда упрощающая формула ищется только для отдельных выражений. Для этого правой кнопкой мыши вызывается локальное меню с командами, применимыми к математическому выражению, а через него вызывается диалоговое окно свойств выражения Properties[38]. В этом окне у позиции Enable Optimization (возможность оптимизации) ставится флажок[39]. Включенный тем или иным способом режим оптимизации суммы (произведения, интеграла, дифференциала – всего, что можно заменить более простой формулой, – см. первые страницы справочников по высшей математике) заставляет систему Mathcad вспомнить о лаврах Гаусса и отказаться от лобовой атаки. Если более оптимальное решение найдено (его поиск отображается мерцанием на экране докторской четырехуголки – признак того, что работает символьная математика), то правее выражения появляется красная шестиугольная звезда[40]. Свершилось чудо – машина стала считать не только быстрее, но и умнее. Пользователь может просмотреть не только численный результат, но и аналитическое выражение, упростившее расчеты (заменившее собой сумму). Оно заносится в специальный буфер, отображаемый на дисплее командой Show Popup в локальном меню или щелчком по красной звездочке.

Программисты могут здесь вспомнить оптимизирующие компиляторы, вмешивающиеся не только в кодирование алгоритма, но и в упрощение формул. Ввел программист строку S := (A * A - B * B) / (A - B), нажал Enter, а на экране – S := A + B.
Оптимизация в задаче маленького Гаусса – это стрельба из пушки по воробьям: отрезок суммируемого ряда надо значительно увеличить, «чтобы почувствовать разницу» во времени счета. При каком значении n такая оптимизация оправдана – это новая оптимизационная задача: оптимизация, так сказать, в квадрате. Оставим ее для студенческих лабораторных работ, а сами стрельнем из пушки не по воробьям, а по... двум зайцам и покажем, что в ряде случаев оптимизация не только ускоряет расчеты, но и повышает их точность. Скажем осторожнее – влияет на точность. И не только количественно, но и качественно – за счет исправления методологических
ошибок (промахов) численных методов и их конкретных оптимизаций в среде Mathcad.
Упоминавшийся пример оптимизации интеграла из документации к пакету Mathcad тривиален – ясно, что криволинейная трапеция (сам интеграл) и набор маленьких вписанных прямоугольников (приближение к интегралу) никогда не сравняются по площади. А вот более сложный пример (рис. 7.15), показывающий двойственность процесса оптимизации.

Загадка оптимизации

Какой ответ (лобовой – 25 007 600 или хитрый – 24 999 750) правильный, сказать трудно. Автор не стал отыскивать оптимизационный алгоритм или расчетную формулу, а составил BASIC-программу и использовал ее в качестве «третейского судьи» (см. рис. 7.16). Ее запуск выдал на дисплей второе число (24 999 750), что свидетельствует в пользу «второго зайца» – оптимизация не только ускоряет расчеты, но и делает их более точными даже при работе с целыми числами. Математики, к которым автор обратился как к высшим судьям, подтвердили правильность расчетной формулы и дефектность прямого счета. Дело, по-видимому, в том, что на языке C (а на нем писался и Mathcad и Maple V) очень просто запутаться в циклах с пересекающимися параметрами, если при этом нужно оптимизировать еще и саму программу.
Dim n As Integer
Dim i As Integer
Dim j As Integer
Dim k As Integer
Dim S As Long
n = 100
S = 0
For i = 1 To n
   For j = 1 To n - i
      For k = 1 To n
         S = S + k
      Next
   Next
Next
Print “Ответ:”; S
Запуск программы
Ответ: 24 997 500

BASIC-программа – «третейский судья»

Но и с BASIC-программой на рис. 7.16 не все так просто – в цикле с параметром j может оказаться и оказывается так, что n-i (конечное значение параметра цикла) становится меньше единицы (первое значение параметра цикла). В этом случае заголовок цикла должен оканчиваться оператором Step - 1. В нашей же программе шаг изменения параметра по умолчанию всегда равен плюс единице (см. также описание цикла for в этюде 6).
Рассказывая о преподавателе математики, который пришел в восторг от новых ключевых слов expand и series, до предела упрощающих составление вопросов для экзаменов, автор высказал опасение, что абитуриент пронесет на экзамен ноутбук и без труда все решит. Именно «пронесет», а не принесет. За стилистическими различиями скрывается большая проблема, связанная с принятием или непринятием компьютерной математики в преподавании школьных и вузовских дисциплин.
После того как автор стал использовать пакет Mathcad в курсе «Оптимизация химико-технологических процессов», ход занятий кардинально изменился. Раньше разбору сути научно-технической проблемы удавалось отводить не более 20% учебного времени, а остальные аудиторные часы «уходили в гудок» – тратились на разъяснение методов оптимизации и способов их реализации на языках BASIC, C, fortran. Пакет Mathcad и ему подобные перевернули эту ненормальную пропорцию: появилась возможность быстро и элегантно (у английского слова smart есть и другой перевод – «элегантно») решать поставленные задачи без кодирования алгоритма, а в естественном их представлении не только численно, но и аналитически. К программированию приходится прибегать лишь в крайних случаях, когда стандартных средств не хватает. А среда Mathcad позволяет дополнять свой арсенал новыми функциями, программируя их (см. этюд 6). Но эта работа – удел избранных. Основная масса студентов никогда серьезно программировать не будет. Учить их программированию для заполнения графика учебной нагрузки можно, но эффект от этого будет минимальным, а удовольствия никакого. Как игра на скрипке требует особого музыкального слуха, так и написание серьезных программ немыслимо без особого программистского чутья («слуха»), которым обладают далеко не все.

Сейчас в среде преподавателей живо обсуждается вопрос о месте компьютера в процессе изучения высшей математики. Реакций на появление описываемых в книге инструментальных средств две: (а) «держать и не пущать» и (б) кардинально менять методику и содержание учебных курсов. Калькуляторы ликвидировали устный счет как род занятий по арифметике. Автор, учась в начальной школе, должен был через три секунды дать правильный ответ на вопрос: «Сколько будет, если помножить 89 на 76?» Теперешним школьникам, вооруженным калькуляторами, такие вопросы могут только в страшном сне присниться. Здесь впору и сожалеть: устный счет – прекрасная гимнастика для ума. Недаром старый Болконский мучил княжну Марью алгеброй, а самые знаменитые биржевые аферисты – прекрасные математики (вспомним финансовую пирамиду из этюда 5). Есть опасение (или надежда – кому как), что средства символьной математики ликвидируют такие формы практических занятий, как поиск пределов, интегралов, разложение функции в ряд, дифференцирование и др. А это львиная доля содержания семинаров по математике.

Проблема же компьютера на вступительном экзамене по математике снимается довольно просто: если абитуриент с его помощью решит все задачи, то ему впору не пятерку ставить, а диплом выдавать.

На самом деле реакций на появление средств символьной математики не две, а три. Третья реакция определяется не отношением преподавателей к этому ноу-хау, а отношением общества к самим преподавателям. При нынешнем уровне оплаты учителям впору спасибо говорить лишь за то, что они входят в аудиторию и ведут занятия по накатанному пути и на довольно высоком уровне. О кардинальной переделке методики и содержания учебных курсов не может быть и речи. Для этого к занятиям нужно основательно готовиться[41], а времени нет: чтобы прокормить семью, надо халтурить (образчик такой «халтуры» перед глазами читателя). Да и сама символьная математика пока не так совершенна, чтобы можно было все бросить и ухватиться за нее. Тот же Гаусс в гробу перевернулся бы, если б увидел, как пакет Mathcad оптимизировал его несколько измененную школьную задачу. Оказывается, что перестановка слагаемых местами меняет сумму.

Парадокс режима оптимизации

Подобная неприятность случается и при использовании оптимизирующих компиляторов, о которых мы уже упоминали и работать с которыми нужно очень осторожно. Автор когда-то долго бился над одной программой, пока не понял, что оптимизирующий компилятор упорно выносит за рамки цикла системную переменную, считая ее константой. Ошибки вычислительной математики, как правило, понятны и простительны, ошибки же символьной математики иллюстрируются пословицей: заставь дурака богу молиться – он и лоб расшибет. Фокус рис. 7.17 в том, что там решается квадратное уравнение, у которого, как известно, два корня. В практических расчетах отрицательный корень часто отбрасывается. Его принимают за пришельца из потустороннего мира (отрицательная масса, концентрация, абсолютная температура и т.д.). Символьная математика, желая угодить пользователю, подсовывает ему один корень, но не тот, какой надо. Оба корня (100 и -101) найдены на рис. 7.17.
В Руководстве пользователя Mathcad запрещается в суммах давать верхнему пределу значение меньше, чем нижнему. В этом, наверное, заключается ключ к разгадке проблемы на рис. 7.17. Программа же на рис. 7.16 имеет циклы с положительным единичным шагом параметра, что не вполне соответствует суммам на рис. 7.15 (см. описание цикла с параметром в этюде 6).
Но шутки, тем более грубые, в сторону. Реакция «держать и не пущать» вполне обоснована. Опыт западных университетов показывает опасность подмены традиционных занятий изучением математических пакетов[42]. В процессе решения огромная роль отводится постановке учебной задачи и интерпретации результата. Освоение машинной математики может создать иллюзию освоения самой математики: студент, выполнив кучу команд и получив на дисплее массу чисел, формул и графиков, не знает, что с ними делать дальше, и не понимает, где кроется настоящее решение. Из-за этого многие преподаватели вполне обоснованно считают, что включение в уроки математики компьютера равносильно... дооборудованию спортивного тренажера гидроусилителями[43]. Другое дело старшие курсы, где математический аппарат применяется для решения конкретных научно-технических задач.
В седьмой версии Mathcad символьная математика проникла и в программирование – см. рис. 7.18.

Символьная математика и программирование

Символьная математика пока плохо стыкуется с программами Mathcad. Стоит программы на рис. 7.18[44]
слегка усложнить, как тут же появляются сообщения об ошибке. Особенно несовместимы с символьной математикой операторы if, otherwise, break, continue и return (острые углы, которые не терпит природа). В программирование Mathcad проникли пока только зачатки символьной математики из пакета. Подождем новой версии Mathcad, а сейчас обратим свои взоры к Maple V.

Путешествие» тройки в среде языка BASIC

Этот протокол показывает, что происходит манипуляция исходной тройкой сначала прямыми (степень, тангенс), а потом обратными (корень, арктангенс) действиями, в связи с чем в переменную e возвращается уже нетройка (тройка с хвостиком).
В среде Mathcad (рис. 7.20) текстовый режим ввода выражений заменен на графический. Кроме того, знак присвоения «=» заменен на знак «:=», а оператор print реализуется через Mathcad-оператор «=». Но это сути дела не меняет: тройку постигла та же печальная участь, что и на рис. 7.19.

Примеры трех основных команд символьной математики

2. Некоторые команды символьной математики требуют, чтобы перед их выполнением курсором была отмечена переменная, к которой данная команда адресуется (см. верхний предел интеграла в пункте 2 на рис. 7.1 и аргумент синуса на рис. 7.2). В меню Mathcad 7 и 8 Pro[3] в отличие от более ранних версий пакета такие пять команд (Solve – решить относительно переменной, Substitute – заменить переменную, Differentiate – дифференцировать по переменной, Integrate – интегрировать по переменной, Expand to Series – разложить в ряд и Convert to Partial Fraction – преобразовать в элементарные дроби) объединены в подменю Variable[4]. Человек привык, что x – это переменная, k – константа. Если человеку предложить найти корень уравнения a x=b, то он сразу выдаст ответ (x=b/a) без дополнительных вопросов. Mathcad таких условностей (умолчаний) не признает и требует указания переменной дифференцирования, интегрирования и т.д. В остальных случаях достаточно, чтобы все выражение было выделено курсором, как это было сделано с интегралом и дифференциалом пункта 1.1 на рис. 7.1. Можно выделить только часть выражения и применить нужную команду (например, Simplify – упростить) только к ней: было x×x+x×x, получили x2+ x×x, а не 2×x2, если перед упрощением курсором была охвачена не вся сумма, а только первое слагаемое[5]. Если правильного выделения нет, то соответствующая позиция меню Symbolic недоступна и, как это принято, прописана не черным, а серым цветом, призывающим пользователя исправить оплошность. Более опасный случай – это неверное выделение которое тем не менее, не блокирует команды меню. Так, в конце рис. 7.2 не было сделано должного упрощения из-за того, что курсор не охватил всего исходного выражения, а просто был помещен на синусе.
3. Если команда пункта 2 (решение уравнений) адресуется не к уравнению, а к выражению, то по умолчанию считается, что оно приравнено к нулю. Если решений более одного, то они выводятся в виде вектора. Решаться могут не только уравнения, но и неравенства. На рис. 7.3 показано, как с помощью команды Solve решается неравенство, которое мы уже пытались решить графически на рис. 6.25, иллюстрируя работу оператора on error.

Путешествие» тройки в среде Mathcad

Пакет Maple – это, грубо говоря, BASIC-интерпретатор, к которому «прицепили» более 2500 встроенных функций, решающих разнообразные математические задачи: поиск корней уравнений и систем, построение графиков, оптимизация, линейная алгебра, интегральные преобразования, линейное программирование, статистика, тензорный анализ, анализ функций комплексных переменных, теория графов, комбинаторика и многое другое.
Основной (а для многих пользователей – единственный) режим работы Maple – это режим немедленного выполнения команд строки. Как и в среде BASIC, они вводятся в виде текста, а двоеточие служит разделителем операторов. На экране дисплея в среде Maple по умолчанию строки ввода прописаны красным цветом, графический отклик системы – синим, а комментарии пользователя – черным. У языка GW-BASIC цветового выделения не было (впервые этот прием был использован в языке Quick Pascal, а сейчас расцвечивают почти все программы[49]). Готовность интерпретатора «слушать» очередную фразу пользователя (который постепенно переставал быть программистом) отмечалась восклицанием Ok, аналогичным слову «прием» у радистов. А вот как выглядит «кругосветное путешествие» тройки в среде Maple (рис 7.21).

Путешествие» тройки в среде Maple

Глядя на рис. 7.19-7.21, можно утверждать, что Maple – это BASIC, в котором поменяли идеологию (структуру хранения и обработки данных); а Mathcad – это BASIC, в котором изменили интерфейс. Короче говоря, Maple – это BASIC сегодня. (Сравнение, конечно, еще то! Вспомним другое: «Сталин – это Ленин сегодня». Автору в свое время набили голову всякой идеологической мурой, которая всплывает из глубин памяти в самые неожиданные моменты. Вот еще одно идейно выдержанное определение: «Mathcad – это материалистическое направление развития языка BASIC, а Maple – идеалистическое».)
Интерфейс Maple ориентирован на тех пользователей, которые уже набили руку на программировании в средах традиционных языков с вводом сложнейших формул в текстовом режиме. Для таких людей ввод квадратного корня и других математических операций с помощью нажатия соответствующих кнопок на панелях инструментов (технология Mathcad – см. рис. 1.3 в этюде 1) – чистой воды профанация. Редактирование в графическом режиме ранее введенной формулы для них часто становится вообще неразрешимой задачей. Те же, кто с пеленок вкусил легкость и удобство ввода формул в их естественной «многоэтажной» математической нотации Mathcad, морщат нос от всяких там sqrt, int, diff (корень, интеграл, дифференциал – технология Maple) и т.д. Именно на них ориентирован интерфейс Mathcad, и в этом, наверное, одна из причин его популярности. В пятой версии Maple появилась возможность ввода текстовых заготовок функций через нажатие соответствующих кнопок – см. рис. 7.21.

Роковое путешествие» тройки в среде Maple

Протокол на рис. 7.22 почти полностью повторяет протокол на рис. 7.21, только в формулах число 77 заменили на 2, а число 99 – на 3. Задачу упростили, но тем не менее исходная тройка в ней безвозвратно потеряна. Вместо нее вылезло комплексное число, на тройку совсем не похожее. Ошибки вычислительной математики искажают числа слегка (см. рис. 7.19 и 7.20), ошибки символьной математики почти всегда бывают фатальны. Но чаще приходится говорить не об ошибках, а о взаимном недопонимании пользователя и программы. Фокус рис. 7.22 состоит в том, что арктангенс – это не совсем обратная тангенсу функция, а квадратный корень из числа – это не совсем то же, что число в степени одна вторая. Еще раз повторяем, что без хорошего знания математики к Maple лучше не обращаться.
Одно время, когда персональные компьютеры были у нас новинкой, за работающим у дисплея человеком пытались наблюдать психологи. Наблюдать и делать выводы, которые, как правило, были двух сортов: психолог либо формулировал всем известную истину либо психолог изрекал явную глупость. Умный психолог выбирал третий вариант – он молчал. Что-то подобное можно отметить, анализируя работу символьной математики. Несложно придумать пример (см. рис. 7.22), на котором она «сломается» и выдаст «неправильный» результат (Mathcad и BASIC задачу на рис. 7.22 решают «правильно»). Более-менее простые аналитические преобразования выполняются вручную, и компьютер ничего нового здесь не открывает. Обычная (увы) реакция компьютера на сложные задачи – молчание (см. рис. 7.24, где показана попытка аналитического решения дифференциальных уравнений).

Решение дифференциального уравнения в среде Maple

Инструменты символьной математики Mathcad (см. рис. 7.5) позволяют найти за раз только одно из решений (без констант) дифференциального уравнения, записанного на рис. 7.23. Пользователю при этом придется поработать головой и руками, преобразуя исходное уравнение в интегральное, копируя промежуточные выкладки и т.д. Поэтому знание математики нелишне и при работе с Mathcad.
Возвращаясь к теме интерфейса Maple, отметим, что документ Maple может быть структурирован
пользователем: если щелкнуть по кнопке, расположенной левее названия параграфа, то соответствующая область захлопнется и останутся только название параграфа и кнопка – но уже не с минусом, а с плюсом внутри. Это очень удобно при работе с объемными документами. Такая технология заложена во многих Windows-приложених, например в текстовом редакторе Word. В последних версиях Maple и Mathcad допустимы гипертекстовые ссылки.
Как понимает читатель (вернее, знает из курса высшей математики), далеко не всякое дифференциальное уравнение имеет аналитическое решение, описываемое комбинацией известных математических функций и операторов, да и не всякое существующее аналитическое решение удается найти. Кроме того, очень часто аналитическое решение бывает настолько громоздким, что от него приходится отказываться, особенно если нужно найти решение в точке (задача Коши). На рис. 7.24 решается известная задача о развитии эпидемии из этюда 5. Напомним суть задачи. В городе с 22 тыс. жителей появляются 50 инфекционных больных, что вызывает эпидемию. Предположим, что прирост больных за день пропорционален (с коэффициентом Pr[52]) произведению числа здоровых (еще не переболевших и не приобретших иммунитет) на число больных. Спрашивается, как развивается эпидемия, то есть как изо дня в день (переменная t) меняется число больных (функция x) и число здоровых (y). Проблема сводится к решению задачи Коши для системы двух обыкновенных дифференциальных уравнений.

Задача об эпидемии в среде Maple

Maple решил систему аналитически. Но что с этим «решением» делать дальше?!
На рис. 7.25 представлен протокол решения в среде Maple задачи о равновесии балки (решение этой задачи в среде Mathcad дано на рис. 1.15 и рис. 1.16 в этюде 1) – поиск реакций опор x, y и Р, которое сводится к решению системы трех алгебраических уравнений, описывающих баланс сил и их моментов. Задача решается полностью на аналитическом уровне и заканчивается формированием функции y, по которой строится трехмерный график.

Задача о пожарном ведре в среде Maple

Вот некоторые отличия в идеологиях Mathcad и Maple:

Maple-документы должны начинаться с команды restart. Дело в том, что в среде Mathcad действие оператора «:=» распространяется вниз и вправо в текущем документе. В среде же Maple действие оператора присвоения распространяется не только во все стороны документа, но и на другие открытые документы. Команда restart – это своего рода «санитарный кордон», пересекающий действие ранее объявленных переменных, функций, библиотек и т.д.;

Maple более близок к традиционным языкам программирования из-за текстового режима ввода строк. Все математические кнопки Mathcad в среде Maple имеют буквенную кодировку: квадратный корень – sqrt, интеграл – int, дифференциал – diff и т.д. Нужно также помнить латинскую транскрипцию греческих букв: alpha, beta, gamma и т.д.;

при построении декартова графика в среде Maple нет необходимости указывать число точек на графике. По умолчанию их 50. Этот принцип перешел в среду Mathcad, но не полностью. Забегая вперед – к рис. 7.27, следует отметить, что в среде Maple до предела упрощена и процедура построения поверхности: достаточно сообщить имя функции двух переменных и диапазон изменения аргументов. Размер сетки (grid) и другие параметры поверхности задаются по умолчанию. В среде Mathcad построение поверхности сопряжено с предварительным заполнением матрицы значениями функции двух переменных. При этом значения аргументов терялись, вместо них появляются эрзац-аргументы – номера строк и столбцов матрицы;

в среде Maple есть функция maximize, возвращающая максимальное значение (естественно, символьное) анализируемой функции. В среде Mathcad похожее действие производит функция max, возвращающая элемент вектора или матрицы с максимальным значением.

Лобовая атака на три пожарных ведра (рис 7.27) в среде Maple не удалась (численное решение задачи на рис. 2.7).

Задача о трех пожарных ведрах в среде Maple

Минимум функции Розенброка в среде Maple (рис. 7.28) отыскивается без проблем.

Функция Розенброка в среде Maple

В этюде 3 мы решили задачу о краске – задачу линейного программирования. А вот как в среде Maple решается другая подобная задача – об оптимальном плане выпуска стульев.
Суть задачи. Мебельная фабрика может выпускать стулья двух типов – по 8 и 12 тысяч рублей. Под этот заказ выделены материальные и людские ресурсы: 440 погонных метров досок, 65 квадратных метров обивочной ткани и 320 человеко-часов. Известно, сколько досок, ткани и времени идет на изготовление каждого стула:

Стул		Расход досок, м		Расход ткани, м2		Расход времени, чел.-час.
Первый		2		0.5		2
Второй		4		0.25		2.5
Ресурс		440		65		320

Спрашивается, как нужно спланировать производство стульев, чтобы наделать их ценой поболее. Это и отображено в отчете о решении задачи на рис. 7.29.
Данная задача относится к широкому классу задач под названием задачи линейного программирования: необходимо установить план (программу!) выпуска изделий (у нас это стулья), ориентируясь на целевую функцию (общая стоимость стульев) и принимая во внимание ограничения
(ресурсы по доскам, ткани и человеко-часам).

Решение задачи о стульях в среде Maple

Для решения задачи линейного программирования в среде Maple подгружается специальная библиотека simplex. При этом появляется предупреждение (Warning) о новом содержании функции maximize. Функция inequal из библиотеки plots позволяет визуализировать решение задачи линейного программирования с двумя переменными: прямые линии отсекают лишнее и оконтуривают область существования решений (затемненная область). Решение задачи находится на одной из вершин полученного многоугольника и отыскивается модернизированной функцией maximize.
В среде Maple функция solve (решить) имеет много модификаций, определяемых префиксом. Просто solve решает алгебраические уравнения и системы, dsolve - дифференциальные и т.д.
В протоколе на рис. 7.30 функция rsolve ищет рекуррентные (r) формулы для поиска чисел Фибоначчи (см. в этюде 6 рис. 6.13 и 6.14).

Аналитическое решение неравенства

4. Команда пункта 1.2 на рис. 7.1 (вывод числового значения выражения с плавающей десятичной точкой[6]) введена в Mathcad по двум причинам. Во-первых, она позволяет делать расчеты с точностью до 4000 знаков – см. диалоговое окно Float Point Evaluation. Три точки в конце команды Float Point… (они есть и в команде Expand to Series… – разложить в ряд) означают, что перед ее выполнением последует уточняющий вопрос. В нашем случае – это точность, с которой отмеченное выражение должно быть вычислено. Обычный (не аналитический, а вычислительный) оператор Mathcad «e=» выводит основание натурального логарифма с не более чем пятнадцатью знаками в мантиссе. В пункте же 1.2 на рис. 7.1 число e вычислено с 20 знаками. Во-вторых, символьная математика пакета Mathcad оперирует некоторыми функциями, которых в самом пакете Mathcad либо нет, либо они там есть, но называются по-другому[7]. Вывести значения таких функций (на рис. 7.1 это интегральный синус Si и интегральный косинус Ci) можно через команду пункта 1.2. Объясняется это тем, что символьная математика – это не развитие пакета Mathcad, а приобретение фирмы MathSoft у фирмы Waterloo Maple ¾ у разработчика пакета символьной математики Maple V (см. раздел 7.4[8]). Отсюда некоторые нестыковки. В пакете Maple V в вычислениях возможны 64 000 (студенческая версия) и 500 000 знаков (профессиональная версия) в мантиссе[9].
5. Нередко при символьных преобразованиях из-за того, что используется чужая разработка (см. выше), ответ получается настолько не вмещающимся в рамки Mathcad (ни по форме – см. Si и Ci, ни по содержанию – число знаков), что он (ответ) не выводится на экран, а по разрешению пользователя заносится в буфер обмена Clipboard (см. пункт 1.2 на рис. 7.1, где вычислялось число p с 4000 знаками). Что с ним делать дальше, пользователь решает сам. Ответ можно перенести в среду Maple V и там «разделать», а можно попытаться вручную доработать в среде Mathcad, уточнив в help’е или в справочнике по высшей математике, что такое интегральный синус Si, интегральный косинус Ci и другие специальные функции. Нестыковки символьной математики объясняются еще и тем, что в сам Mathcad встроено много функций, которых либо нет в среде Maple V, либо они там есть, но называются или работают по-другому. Пример – функция Maximize (Minimize). В среде Mathcad она возвращает координаты максимума (минимума) функции пользователя (см. этюды 2



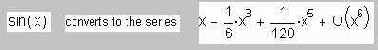
Техника аналитических преобразований с помощью команд меню Symbolic довольно проста:

пишется или откуда-то копируется исходное выражение (см. пункт 1.1 на рис. 7.1), уравнение (пункт 2) или неравенство (рис. 7.3) – делай раз;

в выражении (уравнении, неравенстве) курсором отмечается переменная (фрагмент или вся конструкция) ¾ делай два;

отдается нужная команда из меню Symbolic – делай три.

По умолчанию ответ (упрощенное или преобразованное выражение, корень, число, ряд и т.д.) появляется под исходным выражением, проталкивая вниз то, что было там записано ранее – см. опцию Vertically, inserting lines (вертикально, вставляя строки) в диалоговом окне Evaluation Style (стиль преобразований) на рис. 7.1. По такой схеме на рис. 7.1 сделано самое первое символьное преобразование ¾ взятие неопределенного интеграла от натурального логарифма. Команда[13] Evaluation Style… (последняя в меню Symbolic), вызывает одноименное вышеназванное диалоговое окно, позволяющее отойти от умолчаний в таких направлениях:

ответ можно получить ниже, но без ввода дополнительных строк (опция Vertically, without inserting lines);

ответ можно получить правее исходного выражения (опция Horizontally);

ответ может быть предварен комментарием (флажок Show Comments – см. операцию взятия производной в пункте 1.1 на рис. 7.1; комментарий системы пользователь может дополнить, сделать, например, его перевод с английского);

ответ может быть записан вместо исходного выражения (опциональный флажок Evaluation in Place).

Троица команд Упростить, Дифференцировать по переменной и Интегрировать по переменной (найти функцию, дифференциал которой – исходная функция) составляет ядро символьной математики Mathcad. Для многих студентов и инженеров этими командами (операциями) ограничивается сам математический анализ.

Из команд меню Symbolic заслуживают особого внимания преобразования Лапласа. Автор неравнодушен к математике[14], но любовь к некоторым ее разделам приходила с годами и с трудом. Но к операционному исчислению (в его основе лежат эти самые преобразования Лапласа) любовь пришла, можно сказать, с первого взгляда – сразу после того, как преподаватель у доски показал фокус: «накрыл» выражение шляпой преобразования Лапласа и поднял ее... Без этого раздела математики невозможно представить такие научные дисциплины, как «Теория автоматического управления», «Основы теории цепей»[15]

и др. С помощью обычных двух линеек (простейшая механическая аналоговая вычислительная машина (см. раздел 7.5), где аналог числа – расстояние) можно складывать и вычитать. Если числа нужно перемножить (поделить), то у линеек шкалы делают логарифмическими, что позволяет умножение (деление) свести к сложению (вычитанию) – ведь логарифм произведения равен сумме логарифмов сомножителей. Так устроена обычная (арифметическая) логарифмическая линейка. Преобразования Лапласа можно назвать алгебраической логарифмической линейкой. Они позволяют дифференцирование (интегрирование) заменить умножением (делением). Вот как выглядит «кругосветное путешествие» синуса (поиск производной у функции, а затем поиск первообразной у производной функции) с помощью преобразований Лапласа в среде Mathcad (рис. 7.4).

Maple и числа Фибоначчи

В книге рассматриваются программы, работающие под управлением Windows. Эта операционная система позволяет интегрировать различные прикладные пакеты, а возможность перебрасывать задачу из одной программной среды в другую, избегая их отрицательных качеств и эксплуатируя положительные, – уже путь к успеху. Кроме того, не следует забывать о гибридности решения задач...

Гибридное решение задачи о пожарных ведрах

Далее делается попытка решить полученное уравнение (производную, приравненную к нулю) ¾ найти значение угла вырезки a, при котором объем пожарного ведра будет максимальным (там производная равна нулю). Пакету Mathcad такая работа окажется не по зубам: будет выдано сообщение о том, что ответ настолько «неприличен», что его стыдно показывать, а надо прятать в буфер обмена. Из буфера обмена такой специфической ответ можно перенести в Mathcad-документ текстом (для этого готовится текстовая область – нажимается клавиша «“») или числом. В тексте на макроязыке Maple зафиксирована попытка решения уравнения. Числовое решение позволяет еще раз убедиться в том, что Mathcad обладает зачатками чувства юмора: сообщается, что корни есть. Первый из них (360 градусов) можно отбросить сразу – при таком «раскрое» круглой заготовки объем не максимальный, а минимальный. Второй же «корень» (Root) иллюстрирует принцип: «каков вопрос – таков и ответ». Но если пользователь по-прежнему желает получить аналитический ответ, он должен вернуться к исходной производной и помочь пакету Mathcad решить уравнение, приняв во внимание тот факт, что если один из сомножителей равен нулю, то равно нулю и все произведение. Преобразует же исходное выражение к произведению отдельных сомножителей команда факторизации (Factor), которую мы довольно подробно рассмотрели, анализируя простые числа (рис. 7.11). На рис. 7.31 команда Factor не только нашла произведение, но и упростила выражение для производной, что позволило свести решение к поиску корней квадратного уравнения.
Аналитическая попытка решения задачи о двух ведрах (пункт 2 на рис. 7.31) оборвалась на самом первом шаге – на попытке взятия производной. Но решение у задачи есть, и автор предлагает читателю найти его гибридным методом, комбинируя число, символ и интуицию.
На рис. 7.32. представлено решение задачи о бесконечном числе коробок (см. схему раскроя в пункте 1 на рис. 7.15) с бесконечным числом пропорций выкройки, найденное безо всякого компьютера Б.С. Кушнером из г. Жигулевска Самарской области.

Гибридное решение задачи о коробках

Вторая сторона проблемы повернута, как это ни покажется странным, из области науки в область искусства и даже религии.
Есть люди, способные настроиться на определенный лад, вспоминая любимые стихи, напевая приятную мелодию, мысленно представляя себе живописный пейзаж[58]. А есть счастливчики, расширяющие во время такой душевной медитации список изящного. Они, например, отслеживают про себя побайтный обмен данных на шине компьютера, составляют в голове программу для него или доказывают математическую теорему: Как мысли черные к тебе придут, откупори шампанского бутылку иль пере... реши задачу Коши. Ответ же ищется и численно, и аналитически, и... интуитивно. Присниться может не только таблица химических элементов (и не только Менделееву), но и... неведомое семейство кривых или небывалая структура данных.
По мнению таких «чудаков» (а на них держится настоящая математика), взятие интеграла на ЭВМ равносильно... сочинению стихов на компьютере. И в плане кощунственности самой мысли, и в плане практической, а тем более общеобразовательной (эстетической) пользы. Мы недаром подчеркнули триединство процесса решения задачи. Численные и даже аналитические методы можно отдать на откуп машине. Но интуицию...
[1] Тут правильнее говорить о компьютерной математике аналитических преобразований, но у нас уже прижилась калька с английского термина Symbolic Mathematic ¾ символьная математика.
[2] В пятой версии Mathcad порядок производной не мог быть переменной величиной. В шестом Mathcad’е этот недостаток был исправлен.
[3] Приставка Pro (professional) в названии пакета свидетельствует о том, что в него включены и средства символьной математики.
[4] Это деление не совсем логично: Во-первых, есть еще команды символьных преобразований, требующие указания переменной, к которым они относятся, ¾ преобразование Лапласа, например. Во-вторых, команды Expand (разложить по степеням) и Factor (представить в виде произведения) в их операторных аналогах (см. раздел 7.2) также могут требовать указания переменной, относительно которой данное действие производится.

[5] О том, что проще — x2

или x×x, можно еще спорить.

[6] У нас еще говорят «с плавающей десятичной запятой», учитывая тот факт, что на бумаге мы по-прежнему отделяем целую часть от дробной запятой, а не точкой. Из-за этого возможны конфликты при передаче данных из среды Mathcad в среду Excel (см. приложение 9), где нередко при настройке в качестве разделителя в вещественном числе выбирается запятая, а не точка.

[7] Вот полный список таких функций и констант: arcsec, arccsc, arccot, arcsech, arcscsh, arccoth, g, Catalan's constant, Chi(x), Ci(x), csgn(x), dilog(x), Dirac(x), Ei(x), erf(z), FresnelC(x), FresnelS(x), GAMMA(z), hypergeom(n1, n2..., d1, d2..., z), LegendreE(x,k), LegendreEc(k), LegendreEc1(k), LegendreF(x,k), LegendreKc(k), LegendreKc1(k), LegendrePi(x,n,k), LegendrePic(n,k), LegendrePic1(n,k), Psi(n,x), Psi(x), Shi(x), Si(x), signum(x), W(x), W(n,x) и Zeta(s). Если читатель с ними столкнется, работая в среде Mathcad, то ему нужно будет обратиться к help’у.

[8] В шестой и седьмой версиях Mathcad при включении в работу символьного процессора вместо привычного курсора мыши (стрелка) появляется докторская четырехуголка. В четвертой и пятой версиях курсор превращался в кленовый лист: maple по-английски «клен» - фирма Waterloo Maple находится в Канаде.

[9] В сети Internet по адресу ftp.wustl.edu/doc/misc/pi можно найти число ? с 1 500 000 знаками.

[10] Напоминаем, что в среде Mathcad 8 Pro недопустимы буквы кириллицы в именах переменных при символьных преобразованиях.

[11] Не к ночи будет упомянут, хотя «крестная мама» диамата — классическая философия Гегеля вдохновила автора на работу над книгой под условным названием «Философия программирования».

[12] В восьмой версии Mathcad невязка уже не показывается, так как от нее мало было толку

[13] Это не команда, а переключатель режимов символьных преобразований.

[14] Ее не любят только две категории людей: ущербные люди, которые никого и ничего любить не могут, и люди, с математикой незнакомые. Но любовь автора к математике, увы, не совсем взаимна. Автор в свое время не получил должного математического образования. Отсюда некоторые, мягко говоря, «нестыковки», которые настоящий математик обязательно увидит в книге. Пример: взятие производной и дифференцирование — это далеко не одно и то же.


[15] ОТЦ — имеются в виду электрические, а не пролетарские цепи. У дисциплины « Основы теории пролетарских цепей» другое название — «Политэкономия капитализма». У нас в МЭИ ОТЦ блестяще читал профессор Карл Круг, о котором рассказывали такую страшилку. Сдает студент экзамен по ОТЦ, а Круг его прерывает и говорит: «Да вы, батенька, не знаете закона Ома. Что у вас по физике?» Круг перелистывал страницы зачетки, видел тройку по физике, зачеркивал ее и говорил обалдевшему студенту: «Сначала выучите и сдайте физику, а уж потом приступайте к моей дисциплине».

[16] Случай, когда без команд символьных преобразований не обойтись, ниже на рис. 7.10.

[17] В настоящее время компьютерными символьными преобразованиями проверяются выкладки великих математиков. Ни одной ошибки не нашли пока только у «короля» математиков — Гаусса (см. раздел 7.3). Компьютерной математикой стоит контролировать свои собственные аналитические выкладки.

[18]  Новое — это хорошо забытое старое: см. рис.1.4 в этюде 1.

[19] Константа интегрирования, как мы уже отметили ранее, опускается (полагается равной нулю).

[20] В среде Mathcad PLUS 6.0, который у нас до сих пор очень популярен по двум причинам — наличие русифицированной версии и возможность работы под управлением Windows 3.1 на не очень мощных компьютерах («тройки» и «четверки»), направление символьных преобразований оператором g ® задавалось семью ключевыми словами: (factor, expand, series, simplify, complex, float и assume), которые писались до данного оператора. Это было очень неудобно. Во-первых, в ключевом слове можно было сделать ошибку — написать, например, вместо слова Simplify слово Simplifi. В этой ситуации пакет Mathcad ошибку не фиксирует, но и выражение не упрощает.

[21] Команда Simplify меню Symbolic богаче своего тезки-оператора: командой Simplify можно упростить только часть выражения, отмеченную курсором (см. выше).

[22] Единица не входит в множество «простые числа».

[23] Подпись (электронная или обычная) — это гарантия того, что письмо послано именно тем, чей обратный адрес стоит на конверте. Более того, если нужно будет доказать третьей стороне (судье, например) подлинность сообщения, то это можно сделать так, что ни корреспондент, ни адресат не будут это оспаривать.


[24] Такая идиома встречается во многих книгах. При этом как-то упускается из виду, что через пять-десять лет может быть создан компьютер (транспьютер!), который с данной задачей справится уже за приемлемое время. Для такой работы можно объединить разные компьютеры в сеть. Кроме того, «миллион лет» – это не число, а элемент нечеткого множества «очень долго».

[25] Рекорд (самое большое простое число Мерсенна) на 1 июня 1999 – 26772593-1.

[26] Суперкомпьютер, конечно, по меркам 1982 года.

[27] Большая теорема Ферма утверждает, что an+bn=cn только при n2 (32+42=52).

[28] Это делают, конечно, не в среде Mathcad, а с помощью специальных программ, способных возводить в огромную степень огромные числа. Кстати говоря, функция Ferma с выбранными на рис. 7.11 аргументами работает в среде Mathcad 7, но не работает в среде Mathcad 8. Это к нашему тезису о «капризной бабе» под названием символьная математика.

[29] Мартин Гарднер долгое время редактировал рубрику «Занимательная математика» в этом журнале, материалы которой легли в основу его знаменитых книг.

[30] Числа перемножены не оператором n1×n2=, а командой Вычислить символьной математики.

[31] Название приза зашифровано способом, который использовал еще Юлий Цезарь.

[32] В продаже есть и калькуляторы с символьным процессором (например TI-97).

[33] Если n не указано, то возвращается 20 знаков по умолчанию.

[34] Третье отличие команд символьных преобразований от аналогичных операторов: команда float может вывести до 4000 знаков, оператор — до 250.

[35] В шестой версии Mathcad в ходу был термин «SmartMath» — сообразительная математика.

[36] Символ интеграла — это растянутая буква s, первая в слове summa.

[37] Напоминаем, что в среде Mathcad 8 возможен выбор способа численного интегрирования.

[38] У выражения может быть три режима: а) выражение может быть подсвечено (цвет фона отличается от основного — таким образом можно на данное выражение обратить внимание пользователя); б) выражение может быть выключено из расчетов (стать простым комментарием) и в) выражение может быть оптимизировано.


[39] В шестой версии Mathcad командой на локальную оптимизацию служило ключевое слово optimize, поставленное перед выражением. Ключевое слово literally отменяло оптимизацию следующего за ним выражения при включенном режиме глобальной оптимизации. В среде Mathcad 8 также можно включить режим оптимизации всех выражений, а затем через флажок Enable Optimization отключить оптимизацию у некоторых формул.

[40] Намек на то, что самые лучшие математики — это советские евреи.

[41] Становится меньше не только математиков, готовящихся к занятиям, но и просто хороших математиков. Печальная шутка: «Что такое американский университет? Это место, где бывший советский (вспомним красную шестиугольную звездочку на рис. 7.14) на ломаном английском преподает математику китайцам».

[42] Есть горе от ума, а есть горе от компьютеров и, вообще, от горе всяческих плодов цивилизации.

[43] Пример спортивного тренажера казался автору вполне удачным до тех пор, пока он не узнал, что современные тренажеры (тот же Ketler, мелькающий в рекламе по TV) на самом деле оборудованы силовыми приводами, помогающими человеку или тормозящими рычаги в нужный момент. Этим настоящие тренажеры отличаются от простого троса, перекинутого через блок, с грузом на конце.

[44] Этот документ работает в среде Mathcad 7 и не работает в среде Mathcad 8. Ошибки программирования исправлены по принципу «Есть оператор — есть проблема, нет оператора — нет проблемы».

[45] Разработка фирмы Waterloo Maple, Inc., 450 Phillip Street, Waterloo, ON, Canada, N2L 5J2, тел.: 519-747-23, факс: 519-747-5284, http://www.maplesoft.com. Символ V в названии пакета – это латинская буква V (Victory – победа). Далее в тексте мы ее будем опускать – в новейшей версии этого пакета она также опущена – Maple 6. В конце приложения 1 указано, что в Mathcad встроен MKM (MathSoft Kernel Maple), разработанный фирмой Waterloo Maple, Inc.

[46] С другой стороны, «настоящие» научные дисциплины не боятся прилагательного «занимательный»: занимательная математика, занимательная физика и т.д. Но! «Занимательный научный коммунизм» — как вам это понравится?.. Ладно, не будем пинать издыхающего льва — «Занимательная астрология».


[47] Развитие пакета Mathcad для компьютеров Apple Macintosh остановилось на пятой версии, а для DOS — на версии 2.51.

[48] Это был своеобразный протест против господства числа в Computer Science.

[49] Автор давным-давно написал статью о принципах расцвечивания программ и послал ее в журнал «Микропроцессорные средства и системы» (в то время единственный, где публиковались статьи по персональным компьютерам). Статья попала на рецензию… к дальтонику.

[50] Этот принцип применительно к работе на компьютере можно переиначить так: не спеши изучать языки программирования — очень вероятно, что этого не понадобится: программные среды Mathcad и Maple позволяют решать довольно сложные задачи без традиционного кодирования алгоритмов.

[51] В среде языка BASIC ключевое слово print можно заменить знаком вопроса, а в среде Maple совсем опустить — сравните рис. 7.21 и 7.22.

[52] Еще раз напомним, что вычислительная математика Mathcad допускает буквы кириллицы в именах переменных и функций. В символьной математике и Mathcad и Maple этого делать нельзя. Поэтому на рис. 7.24 мы работаем не с переменной Пр, а с переменной Pr.

[53] Приводим цены во французских франках (5 франков » 1 доллар США) из рекламы, помещенной в журнале La Recherche (№ 10’96): Maple V Release 4 — 6450 (3490 — для учебных заведений), Mathcad 6.0 PLUS — 3490, Mathcad 6.0 — 1490. Но самый дорогой математический пакет — это, конечно, Mathematica 3.0 — 8950 (6965). В Москве у фирмы SoftLine (тел. 232-00-23) учебные заведения могут купить Maple за 600 долл., а Mathcad (русскую версию) — за 420 долл. — см. рекламу в конце книги.

[54] Многие молодые читатели их не застали, поэтому автор излагает здесь азы кибернетики.

[55] Главная причина смерти АВМ в том, что на цифровой машине можно смоделировать аналоговую, а на аналоговой цифровую — нет.

[56] Или гибридностью, если вспомнить название раздела книги.

[57] Это возможно только в седьмой версии Mathcad. В более ранних версиях команды символьных преобразований из меню Symbolic с вложенными пользовательскими функциями не работали.

[58] Умный человек никогда не будет скучать с самим собой.

Преобразования Лапласа в среде Mathcad

Магеллан во время своего турне потерял календарные сутки. При интегрировании командой меню Symbolic (см. рис. 7.1 и рис. 7.2) константы также теряются. Кругосветное «путешествие» синуса через преобразования Лапласа (см. рис. 7.4) обошлось без потерь – исходный синус вернулся с константой С за счет того, что в промежуточных выкладках «вылезла» функция Dirac, равная бесконечности при нулевом аргументе и нулю в остальных случаях.
Команды символьных преобразований, собранные в меню Symbolic в среде Mathcad 7 и 8, Pro стали лишними[16]. Эти команды стали неким рудиментом более ранних версий (как функция until), подарком тем, кто к ним привык. Их стоит рассматривать как некие инструменты работы с базой данных по аналитическим преобразованиям (производные, интегралы, ряды и т.д.), которые в виде таблиц помещаются на первых страницах справочников по высшей математике. С одной стороны, к командам символьной математики стоит прибегать и в случае довольно простых преобразований, подобных таким, которые зафиксированы на рис. 7.1 и рис. 7.2. Дело в том, что при ручной работе неизбежны опечатки[17]. С другой стороны, элементарные преобразования следует делать самому. Это, во-первых, тренирует голову, а во-вторых... Все мы сейчас пользуемся телефонами с памятью и, звоня родным или знакомым, просто нажимаем на кнопку с именем человека вместо того, чтобы набрать номер. Все это хорошо, но если приходится звонить близким с чужого телефона, то зачастую вспомнить номер бывает трудно, а в записной книжке его, естественно, нет. Один студент автора не смог вспомнить производную от ex и побежал к компьютеру уточнить, чему она равна...

Решение дифференциального уравнения средствами символьной математики Mathcad

На рис. 7.5 командами символьной математики решается дифференциальное уравнение. Вернее, ищется одно из его решений. Полное решение можно увидеть на рис. 7.5. В конце рис. 7.5 читатель видит новый символ «®»[18], который переводит повествование от команд к операторам символьных преобразований.

Примеры работы оператора символьных преобразований

В ряде случаев оператор «®» возвращает комментарий (см. в пункте 5 ответ “undefined” – «неопределенно») при попытке вычисления предела функции 1/x без указания стороны, с которой мы приближаемся к нулю. В других случаях оператор «®» возвращает само исходное выражение (производную n-го порядка) или выражение с конструкцией, не встроенной в Mathcad, – интегральный синус, например: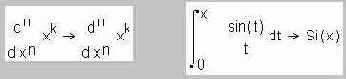

Сейчас мы возьмем задачи из первых этюдов книги и по-новому их решим с помощью оператора «®».
На рис. 7.7 приведено аналитическое решение задачи о купце и сукне из этюда 1.

Аналитическое решение задачи о купце и сукне

Команда Solve из меню Symbolic годится только для решения одиночных уравнений и неравенств. Ее «численные» аналоги – функции root и polyroots. Для решения систем уравнений и неравенств предназначена функция Find, которая способна возвращать как численный, так и аналитический результат в зависимости от того, что за ней проставлено – символ «=» или «®». Во втором случае функция Find не требует первого приближения. На рис. 7.7 функция вернула Find аналитическое решение системы двух линейных алгебраических уравнений, которое было скопировано и в которое были подставлены конкретные значения переменных.
На рис. 7.8 приведен аналитический поиск минимума функции Розенброка (численное решение задачи показано на рис. 3.4), в которой константы 100 и 1 заменены на переменные a и b.

Аналитический поиск минимума функции Розенброка

Здесь через функцию Find аналитически решается система уравнений (пункт 1), собранная из частных производных функции Розенброка по x и y, приравненных к нулю.
Показано, что значение переменной a не меняет положение точки минимума – оно существенно влияет на процесс численного решения задачи, удлиняя овраг, на дне которого находится минимум. В этом можно убедиться, вернувшись к рис. 3.4 и изменив в функции Розенброка сотню, к примеру, на единицу.
Далее на рис. 7.8 в пункте 2 продолжены «деривации» этюда 3: сделаны попытки проверки на «аналитичность» двух других встроенных Mathcad-функций, также предназначенных для решения оптимизационных задач. Функция Minimize отказалась работать (пункт 2.1), а функция MinErr выдала непонятно что (пункт 2.1). Пункт 2 на рис. 7.8 – это по сути протокол экспериментов над программной средой, которые в принципе не возбраняются, но плодами которых нужно пользоваться очень осторожно.
На рис. 7.9 приведено аналитическое решение задачи о балке из этюда 1 (см. рис. 1.12, 1.15 и 1.16).

Аналитическое решение задачи о равновесии балки

Три выражения, которые вернула функция Find (пункт 1), мы использовали в этюде 1 для иллюстрации графических возможностей Mathcad (см. рис. 1.17-1.19 и 1.21-1.25).
В пункте 2 на рис. 7.9 показан и второй способ решения системы уравнений через оператор символьного преобразования с ключевым словом
(здесь ключевое слово solve – решить). Прежде чем описывать эту новую конструкцию, отметим, что в символьных преобразованиях Mathcad перестают работать встроенные единицы измерения: если оба плеча балки измеряются в метрах, то выдается правильный ответ, однако если второе плечо выражено в дюймах – ответа нет.
На рис. 7.10 приводятся образцы заготовок, которые возникают на экране дисплея в отмеченном курсором месте после нажатия клавиш панелей инструментов Evaluation и Symbolic:

Семь замечаний

1. Автор, естественно, постарался исправить ошибки и опечатки первого издания. В этом ему помогли знакомые и незнакомые коллеги, которым автор безмерно благодарен.
2. В качестве официального бета-тестера автор участвовал в испытаниях бета-версии седьмого Mathcad. Это позволило ему, во-первых, заглянуть в «кухню» фирмы MathSoft, а во-вторых, заранее (до выхода программного продукта) основательно «обыграть» новинки Mathcad 7 Pro.
3. Не оставлена без внимания и предыдущая версия Mathcad — Mathcad PLUS 6.0. Дело в том, что седьмой Mathcad предъявляет высокие требования к компьютеру (Windows 95, 16 Мбайт ОЗУ и др.). Книга адресована студентам и инженерам, для многих из которых по техническим причинам даже Windows 3.x недоступен. Есть, кстати, и DOS-версия Mathcad, работающая и на IBM без винчестера, и с 1 Мбайт оперативной памяти. Почти все задачи книги (кроме тех, которые помещены в этюдах 6 и 7) работают и в среде Mathcad под управлением DOS.
4. Автор активно включился в процесс формирования «мирового решателя» задач с использованием Mathcad: все программы книги размещены на серверах.
5. Книга имеет гриф учебного пособия, поэтому при ее переработке были учтены те трудности, с которыми студенты сталкивались при освоении Mathcad с помощью данной книги.
6. Одновременно с написанием книги автор создавал обучающий мультимедийный курс (CD-ROM) по программе Mathcad в фирме «МультиМедиа Технологии» (111116 Москва, ул. Энергетическая, 8/2, тел. (095) 362-74-86, e-mail mmt@glas.apc.org). Автор надеется, что книга и курс выйдут одновременно и дополнят друг друга[1]. На CD-ROM предполагается разместить русскую легальную версию Mathcad PLUS 6.0[2]. Так что его пользователь сбросит с себя груз проблем, описанных в разделе 6.10 данной книги.
7. Автор будет благодарен за замечания и пожелания по книге, которые просит направлять по обычной (111250 Россия, Москва, Красноказарменная, 14, МЭИ, ТВТ) или по электронной (ochkov@twt.mpei.ac.ru) почте. Сами же файлы с задачами книги хранятся по адресу ftp:\\twt.mpei.ac.ru\book.mcd.
И последнее замечание. Люди, много работавшие с языком fortran, знают, что это не просто язык кодирования алгоритмов, а целый мир со своими судьбами, легендами, удачами и неудачами... Среду Mathcad можно и нужно рассматривать не только как среду программирования, но и как некую сферу культуры, составляющую пласт мировой культуры. Эту идею автор постарался пронести сквозь книгу, которую можно и нужно рассматривать, только как учебное пособие по популярной программной среде, но и как сборник рассказов об околокомпьютерной жизни.

Формируя пользовательскую интерполирующую функцию, необходимо

Формируя пользовательскую интерполирующую функцию, необходимо сразу освободиться от размерностей аргументов, приведя их к безразмерной величине относительно данных в боковике (у нас это температура) и шапке (давление) таблицы узловых (опорных) точек. Размерность функции, соответствующая данным в таблице, приписывается к возвращаемой величине в конце формируемой функции.
Все это позволяет иметь в качестве аргументов функции величины с любой допустимой размерностью температуры и давления и получать удельную энтальпию также с различной размерностью (см. рис. 4.10).


Интерполяция, как правило, ведется в оговоренном диапазоне значений аргументов. Поэтому будет целесообразно вставить в функцию пользовательские сообщения об ошибке – о выходе за пределы разумных значений аргументов[13]. Для этого предназначена встроенная в Mathcad функция error(“Сообщение об ошибке”), прерывающая выполнение вычислительной процедуры и своим комментарием призывающая пользователя исправить оплошность. Если пользователь «подсунет» функции hss(T, P), к примеру, не температуру и давление, а массу и длину, то заработает уже встроенное сообщение об ошибке “The units in the expression do not match” (Единицы в выражении не соответствуют правилам – см. рис. 4.11):


Методика двухмерной сплайн-интерполяции, реализованная в Mathcad, требует, чтобы табличные значения двух аргументов хранилась в матрице с двумя столбцами, а табличные значения функции – в квадратной матрице. Для лучшего обзора и редактирования табличные данные можно временно объединить в одной квадратной матрице (у нас ее имя M, а размер (порядок) 19 на 19 – см. рис. 4.10), где первый столбец без первого элемента – это табличные значения температуры (первый аргумент формируемой функции), а первая строка без первого элемента – табличные значения давления (второй аргумент). Последующие манипуляции функцией submatrix раскладывают все «по полкам» – матрица TP с двумя столбцами и с 18 строками хранит табличные значения аргументов, а квадратная матрица H с порядком 18 – табличные значения удельной энтальпии. Так можно добиться компромисса между требованиями Mathcad и требованиями наглядного размещения данных.
Для лучшего обзора исходных данных и для разделения их на функциональные группы в исходной матрице можно записывать числовые константы (элементы матрицы) с различным видом и размером шрифта – см. рис. 4.10 (непронумерованный совет).


Никогда не стоит опираться на конкретное значение системной переменной ORIGIN (номер первой строки и первого столбца матриц) и на конкретный размер матриц. В функции hss(T, P) записан оператор «вырезания куска» из матрицы M – вектора табличных значений температур:
TP¬submatrix(M, ORIGIN + 1, rows(M) - 1, ORIGIN + 1, cols(M) - 1),
а не
TP<0>¬submatrix(M, 1, 18, 1, 18)
Два эти выражения эквивалентны только при ORIGIN=0 (умолчание Mathcad) и при порядке матрицы M, равном 19. При других значениях переменной ORIGIN и при других размерах матрицы M второе выражение при вызове функции hss даст сбой.


Очень часто табличные данные, отображающие значения какой-либо физической величины (удельной энтальпии водяного пара, как в нашем случае), не укладываются в отведенные им в среде Mathcad сугубо квадратные рамки. На место отсутствующих данных (левый нижний и правый верхний угол нашей квадратной матрицы) можно записать что-то, резко отличающееся от «настоящих» данных. У нас это минус единица. Возврат значения функции нужно предварить оператором error (см. предпоследнюю строку на рис. 4.10), прерывающим расчет, если возвращаемое значение «не лезет ни в какие ворота» в смысле порядка величины. В нашем случае с функцией hss(T, P) значение энтальпии не может быть меньше, чем 1930.8 кДж/кг – наименьшее «разумное» значения матрицы энтальпий. Если так получилось, то это означает, что при интерполяции «захвачена» минус единица и решение неверно.


При подготовке Mathcad-документа к публикации стоит переместить копию экрана дисплея (клавиша PrtSc) в среду какого-либо графического редактора (Paintbrush, например) и там его доработать. Основные направления доработки, которыми автор воспользовался, готовя иллюстрации к этой книге:

вертикальная линия, отмечающая начало и конец процедуры формирования функции пользователя hss(T, P) на рис. 4.10, изогнута, что позволило сделать листинг более компактным;

для этой же цели были убраны столбцы, хранящие энтальпию пара при 8, 10, 12, 15, 20 и 22 МПа;

в среде графического редактора в Mathcad-документ можно внести то, что в среде Mathcad не внесешь, например, вертикальный комментарий на месте стертых столбцов и другие пометки – см. рисунки книги;

копируя экран дисплея, можно захватить информацию, которая при простой распечатке Mathcad-документа (команда Print в меню File) пропадает. Это, во-первых, встроенные и пользовательские сообщения об ошибках – см. рис. 4.11. Можно из разных копий экрана дисплея, фиксирующих различные моменты диалога пользователя с компьютером, собрать один: на рис. 4.11 выведены все три сообщения об ошибках, хотя на экране дисплея одновременно можно видеть лишь одну – ту, которая выпадает из «покрасневшей от ошибки» функции, когда пользователь наводит на нее курсор мыши.

На рис. 4.12 проиллюстрирован вызов функции hss(T, P) при различных значениях и различных размерностях аргументов. Размерность возвращаемой функцией удельной энтальпии пользователь также вправе менять.

Translation into English by R.Girvin

This problem of a label – or more correctly, problem of disposing with a label -– we'll look at in solving an ancient English puzzle about fishermen and fish:
"Three fishermen lay down to sleep, not having counted or divided their catch. In the night, one of them woke up, and (not quite trusting the others) decided to divide the pile of fish and take his share. But the number of fish wasn't visible by three. However, he found he could throw one fish away, then take exactly a third. This he did (noting, in the true spirit of fairness, that an even number of fish was left for his comrades) and went back to sleep. Later, the second and third fishermen woke in turn, and each went through the same process. The question is, what is the minimum number of fish in the catch that fulfils these conditions?"
The reader might like first to try to solve this task by hand; but we'll involve the computer in this for two reasons. Firstly, it lets us consider some ways to structuralize programs in the Mathcad environment: methods of clearing programs of labels, and 'squeezing' them into the rigorous framework of structural design. Secondly, we'll show that the Fishermen's Problem has, until now, been solved incorrectly...

A pirate's open letter to computer publications
(Translation into English by R.Girvin)
1. A philosophical-religious aspect of the problem
2. A cultural aspect of the problem
3. A police aspect of the problem
4. A moral aspect of the problem
On opening any issue of any computer publication, one can stumble upon articles concerning the problem of illegal copying and program distribution. This letter broaches this subject, but in a slightly different context. It makes no attempt to condemn or justify piracy. The author merely tries to examine this problem from unusual angles: philosophical, religious, cultural, police, moral ... and even sexual.

Три дивертисмента

1. Дивертисмент политический.
Наши политики, обсуждая статус Чечни (Страны Басков, Корсики и др.) загоняют себя в угол. Мол, независимость – это как беременность: она либо есть, либо ее нет. Нельзя быть чуть-чуть беременной, нельзя быть чуть-чуть независимой и т.д. и т.п.
Это противоречие можно разрешить с помощью теории нечетких множеств. Рассказ о ее основах обычно начинают с парадокса кучи зерна. Сто зерен – это куча или нет? Конечно, нет, – это скорее горсть
зерна. А если к этой горсти прибавить еще одно зерно, станет ли она кучей? Опять нет. А если еще зерно и еще зерно. Рано или поздно мы получим кучу. Люди пытались с позиций классической математики определить точное число зерен, разграничивающее горсть и кучу, но ничего путного из этого не получалось. Примерно так сейчас политики пытаются найти количество признаков (полномочий), отделяющих независимое государство от субъекта федерации. Все бы ничего, да кровь льется.
Дело в том, что понятие «независимое государство» традиционно (исторически) рассматривается как элемент четкого множества. Дескать, государственное образование может либо принадлежать, либо не принадлежать к этому множеству.
Но все намного сложнее и намного проще. Понятие горсть и куча – это нечеткие множества. Сто зерен – это одновременно и горсть и куча. При этом значение функции принадлежности ста зерен к множеству горсть равна почти единице, а к множеству куча – почти нулю. Если к этой сотне добавить зернышко, то первое значение (близкое к единице) чуть-чуть уменьшится, а второе (близкое к нулю) – чуть-чуть увеличится. Опять повторяем – природа не терпит острых углов и черно-белых оценок.
Проблема кучи зерна решается с позиции теории нечетких множеств так: насыпаются разные количества зерен, а люди (эксперты; лица, принимающие решения) дают такие оценки: «это горсть (0)», «это скорее горсть, чем куча (0.33)», «это скорее куча, чем горсть (0.67)», это и не горсть и не куча, а что-то среднее (0.5), «это куча (1)» и т.д. (так сейчас, к примеру, проводят опрос общественного мнения). После этого строится функция принадлежности (см. главку в этюде 6) к нечеткому множеству «куча зерна». График этой функции – плавная и пушистая кривая, поднимающаяся от нуля (мало зерен) к единице (много зерен) без каких-либо скачков. Функция принадлежности к множеству «горсть зерна» имеет «горбатый» график: нули по краям (идем от отдельных зерен к куче) и единица посредине (горсть зерна).

Проблема Чечни – это проблема не только России, но и всего мирового сообщества в том плане, что в уставе ООН заложены два взаимоисключающих принципа – принцип нерушимости границ и право нации на самоопределение (на независимость). Решить эту проблему можно, приняв во внимание, что понятия «нация» и «независимое государство» – это также нечеткие множества. Государственное образование (область, район, республика) может быть и чуть-чуть независимым и совсем независимым. Читатель может сам при желании составить такую таблицу: в первой колонке написать названия стран (включая субъекты Российской Федерации), а во второй – значение функции принадлежности этих стран к множеству «независимое государство». Германия независимое государство или нет!? Вроде бы да, но многие ее суверенные полномочия ограничены членством в НАТО, в Европейском Союзе, в Общем рынке и т.д. Такой важный атрибут независимости, как национальная валюта, и та скоро у Германии пропадет (евро!). Немецкий язык все больше становится неким местным диалектом – все серьезные научные конференции проводятся на английском языке. Так что «независимости» у этой страны сейчас намного меньше, чем у той же Чечни. Говоря языком теории нечетких множеств, можно сказать, что значение функции принадлежности к множеству «независимые государства» у Германии ниже, чем у Чечни. То, что в Бонне много посольств иностранных государств, а в Грозном пока ни одного, ни о чем не говорит. Представим себе, что завтра все страны порвут с Германией дипломатические отношения. От этого статус Германии как независимого государства только повысится. На нашей планете самые независимые – это самые одиозные государства: «алкоголики» (поставщики наркотиков), «тунеядцы» (страны, живущие за счет помощи мирового сообщества), «хулиганы» (Ливия, Ирак, Северная Корея – маленькие «хулиганы», Россия, США, Китай – взрослые «хулиганы»). «Алкоголиков» и «тунеядцев» называть не будем – где здесь вина, а где беда этих стран? «Казнить нельзя помиловать!»

Итак, будем считать, это все субъекты Российской Федерации – независимые государства, но значения функции принадлежности у них к этому нечеткому множеству разные: у Тверской области одно, у Татарстана – другое, а у Чечни третье, самое высокое. В процессе государственного строительства эти числа могут меняться плавно (реформы) либо скачками (революции, войны, но лучше – референдумы), но никогда они не упадут до нуля и не поднимутся до единицы.


2. Дивертисмент политико-компьютерный.

Теории нечетких множеств и нечеткой логики можно приложить и к проблеме компьютерного пиратства. Закон делит всех людей на два четких множества: «множество легальных пользователей программ» и «множество нелегальных пользователей (пиратов)». В реальной жизни все намного сложней: нечетких множеств людей, причастных к компьютерам, великое множество (извините за тавтологию). Есть множество торгующих на «Горбушке» «черными» дисками и есть множество

тех, кто принципиально работает только с легальными копиями и никогда не подаст руки согрешившим – нарушившим какое-либо лицензионное соглашение. Можно осью «грешник-праведник» построить горбатые статистические кривые, описывающие состояние компьютерного рынка в конкретной стране. Где находится максимум этой кривой, куда и с какой скоростью он перемещается во времени?

3. Дивертисмент компьютерный.

Даниил Хармс[33]

подметил, что память – это очень странная штука: иногда запомнишь одно, а вспомнишь потом совсем другое. А бывает и так, что запомнишь настолько крепко, что потом ни за что не вспомнишь.

Основное отличие памяти человека от «памяти» компьютера в том, что человек разную

информацию запоминает по-разному. Одно дело запомнить телефон случайного знакомого, а другое дело такую информацию: «Еще раз сунешь сюда нос – голову оторву!»

Элементарные ячейки памяти цифрового компьютера хранят либо нули, либо единицы, не делая никаких различий по важности информации. «Бит» информации в мозге человека – это нейронная связь различной «толщины», меняющейся, условно говоря, от нуля до единицы. Может быть, стоит заряжать конденсаторы компьютера не ступенькой, а плавно…

Семь дивертисментов к трем дивертисментам.

А вот еще примеры того, что в жизни нет чистых нулей и единиц – нет четких и однозначных ответов на, казалось бы, самые простые вопросы.

1. Считается, что костры в лесу увеличивают опасность пожаров. Но! Туристы, собирающие для костров хворост и сухостой, культурно

сжигают горючий материал, готовый вспыхнуть от удара молнии или от неосторожно брошенной сигареты. Так что костры в лесу не губят (не только губят),а защищают лес от пожара.


2. Российские политики из кожи лезут вон, добиваясь, чтобы транзитные нефтепроводы из района Каспия проходили исключительно через российскую территорию. Считается, что обходные пути перекачки нефти лишат Россию огромных доходов и политического влияния. Но! Влиять на кого-то шантажом перекрытия задвижки крайне аморально. Экономический же эффект транзита нефти может быть подсчитан только после оценки ущерба, наносимого России разрывами

трубопроводов и другими авариями. Мы должны всеми правдами и неправдами добиваться прокладки трубопроводов минуя российскую территорию. Новые трубопроводы нужно прокладывать лишь после того, когда уровень эксплуатации существующих трубопроводов станет приемлемой. Это касается и газопроводов – вспомним, как под Уфой в огне сгорели два пассажирских поезда. В нормальной стране после такой катастрофы любой Газпром разорился бы, выплачивая страховки. А у нас ничего…

3. В настоящее время в мире ведется кампания по тотальному запрещению противопехотных мин. Символ этой кампании –  безногий ребенок на костылях, подорвавшийся на мине, оставшейся от давнего конфликта. Но! Если бы в свое время конфликтующие стороны (например, представители народностей тутси и хуту в Бурунди) не отделили бы друг от друга минными полями, проходы в которых контролировали нейтральные силы (войска ООН, например), то жертв, в том числе и среди женщин, стариков и детей, могло бы быть намного больше. Плохи не противопехотные мины, а люди, забывающие или не умеющие ликвидировать их после окончания конфликта.

4. Расхожий лозунг ура-патриотов: «Если народ не хочет кормить свою армию, то он будет кормить чужую». Мы вскармливали Советскую армию, которая стреляла в мирных людей в Новочеркасске, с позором выходила из Венгрии, Чехословакии, Германии, Афганистана, Чечни... Красную Армию немецкие войска в 1941 году разбили за пару месяцев, а Победу добывал уж сам народ-кормилец (с помощью Мороза-воеводы): инженеры, учителя и прочий рабочий люд на целые четыре года оставили свой мирный труд и взялись за оружие. Про армию трудно судить, но вот отечественную милицию, а тем более ГАИ (ГИБДД) стоило бы поменять на импортную, некоррумпированную (на немецкую, например). Эффективнее и, что интересно, дешевле бы вышло. Армию же вообще не стоит содержать – ни свою, ни чужую. Ракетно-ядерные силы сдерживания – это по своей сути никакая не армия, а научно-техническая отрасль, работникам которой зачем-то погоны прицепили.


5. Оружие у населения у нас считают одним из главных факторов роста преступности. Но! Демократия вместе с порядком (Законом) воцарилась в Западной Европе лишь после того, как крестьяне взяли в руки оружие и стали защищать себя от средневекового рэкета – от произвола синьора. Сможет ли современная «аристократия» («братки[34]», «крыша») обкладывать поборами современных «крестьян» (предпринимателей), зная, что вместо денег можно получить пулю в лоб – и все будет законно. В стране не было бы никакого 37 года, если бы хозяева «черных воронков» (НКВДАПО) боялись хотя бы вооруженного сопротивления арестовываемых.

6. Сейчас ни у кого не поворачивается язык сказать ничего, кроме слов осуждения, в адрес террористов. При этом специально ставят на одну доску людей, захватывающих невинных жертв, и людей, вынужденных браться за оружие для решения своих политических и иных проблем (см. выше). С первыми все более-менее ясно, их нужно рассматривать как некое стихийное бедствие, от которого никто не застрахован. Нужно только стараться под него не попадать, а если попал, то правильно себя вести. Со вторым же типом «террористов» не все так просто. К ним можно отнести принцип «на то щука в море, чтобы карась не дремал». Говорят, что можно устранить любого политического деятеля – все дело в средствах, которые на это можно ассигновать (инвестировать). Того или иного лидера не устраняют не только потому, что у него сильная охрана, но и потому, что это никому пока не нужно. Или нет средств на это. Политический деятель ведет себя прилично, боясь в том числе и пули своих оппонентов (своего народа).

7. Целостность России наши политики возводят в ранг некоего идола, которому нужно приносить огромные жертвы. Но! Все дело в том, что настоящие люди чувствуют себя не только россиянами, но и европейцами, гражданами Мира. Национализм, как верно подмечено, – это последнее прибежище негодяев. Многие русские люди отделились бы от Москвы и присоединились бы, например, к Страсбургу, но не имеют на то сил, а, главное, повода. Уезжать из этой страны? Нет, спасибо! Пусть лучше уезжают те, от кого нам хочется отделиться…

Мысли, конечно, очень спорные и где-то даже извращенные, но… еще раз взглянем на название этюда…

    Биржевой анализ: Технический анализ - Инструменты - Софт

• Биржевой анализ - Технический анализ
  
• Обучение техническому анализу
  
• Индексы технического анализа
  
• Индикаторы технического анализа
  
• Методы технического анализа
  
  
• Графика в техническом анализе
  
• Технический анализ рынков
  
• Российский технический анализ
  
• Инструменты технического анализа
  
  
• Математика в биржевом анализе
  
• Разновидности биржевого анализа
  
  
• Mathematica в биржевом анализе
  
• MathCAD в биржевом анализе
  
• Maple в биржевом анализе
  
• Matlab в биржевом анализе