Математический редактор MathCAD
Назначение Mathcad
1.1. Назначение MathcadMathcad является математическим редактором, позволяющим проводить разнообразные научные и инженерные расчеты, начиная от элементарной арифметики и заканчивая сложными реализациями численных методов. Пользователи Mathcad — это студенты, ученые, инженеры, разнообразные технические специалисты. Благодаря простоте применения, наглядности математических действий, обширной библиотеке встроенных функций и численных методов, возможности символьных вычислений, а также превосходному аппарату представления результатов (графики самых разных типов, мощных средств подготовки печатных документов и Web-страниц), Mathcad стал наиболее популярным математическим приложением.
Mathcad 11, в отличие от большинства других современных математических приложений, построен в соответствии с принципом WYSIWYG ("What You See Is What You Get" — "что Вы видите, то и получите"). Поэтому он очень прост в использовании, в частности, из-за отсутствия необходимости сначала писать программу, реализующую те или иные математические расчеты, а потом запускать ее на исполнение. Вместо этого достаточно просто вводить математические выражения с помощью встроенного редактора формул, причем в виде, максимально приближенном к общепринятому, и тут же получать результат Кроме того, можно изготовить на принтере печатную копию документа или создать страницу в Интернете именно в том виде, который этот документ имеет на экране компьютера при работе с Mathcad Создатели Mathcad сделали все возможное, чтобы пользователь, не обладающий специальными знаниями в программировании (а таких большинство среди ученых и инженеров), мог в полной мере приобщиться к достижениям современной вычислительной науки и компьютерных технологий. Для эффективной работы с редактором Mathcad достаточно базовых навыков пользователя. С другой стороны, профессиональные программисты (к которым относит себя и автор этих строк) могут извлечь из Mathcad намного больше, создавая различные программные решения, существенно расширяющие возможности, непосредственно заложенные в Mathcad.
В соответствии с проблемами реальной жизни, математикам приходится решать одну или несколько из следующих задач:
Знакомство с Mathcad
1.2. Знакомство с MathcadВ данном разделе, несколько забегая вперед, покажем, как быстро начать работу с Mathcad, научиться вводить математические выражения и получать первые результаты расчетов.
Меню
1.3.1. МенюСтрока меню располагается в самой верхней части окна Mathcad. Она содержит девять заголовков, щелчок мышью на каждом из которых приводит к появлению соответствующего меню с перечнем команд:
Чтобы выбрать нужную команду, щелкните мышью на содержащем ее меню и повторно на соответствующем элементе меню. Некоторые команды находятся не в самих меню, а в подменю, как это показано на рис. 1.5. Чтобы выполнить такую команду, например команду вызова на экран панели инструментов Symbolic, наведите указатель мыши на пункт Toolbars (Панели инструментов) выпадающего меню View (Вид) и выберите в появившемся подменю пункт Symbolic.
Далее в книге, говоря о совершении того или иного действия с помощью меню, последовательность выбора пунктов меню будем приводить сокращенно, разделяя их косыми чертами Например, рассмотренная команда обозначается как View / Toolbars / Symbolic.
Панели инструментов
1.3.2. Панели инструментовПанели инструментов служат для быстрого (за один щелчок мыши) выполнения наиболее часто применяемых команд Все действия, которые можно выполнить с помощью панелей инструментов, доступны и через верхнее меню. На рис. 1.7 изображено окно Mathcad, содержащее четыре основные панели инструментов, расположенные непосредственно под строкой меню. Кнопки в панелях сгруппированы по сходному действию команд:
Настройка панели инструментов
1.3.3. Настройка панели инструментовВ Mathcad, подобно другим программам Windows, пользователь может настроить внешний вид панелей инструментов наиболее оптимальным для него образом.
Вы можете:
Вызвать любую панель на экран или скрыть ее можно с помощью меню View / Toolbars, выбирая в открывающемся подменю имя нужной панели (см. рис. 1.5). Убрать любую панель с экрана можно еще и посредством контекстного меню, которое вызывается щелчком правой кнопкой мыши в любом месте панели (например на любой кнопке). В контекстном меню следует выбрать пункт Hide (Скрыть). Кроме того, если панель плавающая, т. е. не прикреплена к основному окну (как, например, все панели на рис. 1.8), то ее можно отключить кнопкой закрытия (на рис. 1.8 указатель мыши наведен на эту кнопку панели Calculator).
Математические панели, в отличие от основных, можно вызвать или скрыть нажатием соответствующей кнопки панели Math. Присутствие или отсутствие математических панелей показано в виде нажатой (или отжатой) соответствующей кнопки (см. рис. 1.3, 1.4 или 1.8).
Создание плавающих панелей
Чтобы открепить любую из панелей от границ окна Mathcad:
Большинство математических панелей могут быть только плавающими
Рабочая область
1.3.4. Рабочая областьБольшую часть окна Mathcad занимает рабочая область, в которую пользователь вводит математические выражения, текстовые поля и элементы программирования. Важно уметь настроить рабочую область для работы, чтобы хорошо ориентироваться в документе.
Строка состояния
1.3.5. Строка состоянияВ нижней части окна Mathcad, под горизонтальной полосой прокрутки, на большинстве рисунков этой главы видна строка (линия) состояния На ней отображается самая основная информация о режиме редактирования (рис. 1.18), разграниченная разделителями (слева направо)
Интерфейс пользователя
1.3. Интерфейс пользователяВ Mathcad интерфейс пользователя интуитивен и сходен с другими приложениями Windows. Его составные части:
Справочная информация
1.4. Справочная информацияВместе с Mathcad поставляется несколько источников справочной информации, доступ к которым осуществляется через меню Help (Справка)
Кроме поименованных, меню Help (Справка) содержит следующие пункты
Диалоговое окно выбора масштаба
Диалоговое окно выбора масштаба
Чтобы выбрать другое значение масштаба отображения документа, необходимо выполнить команду View / Zoom (Вид / Масштаб). В этом случае появляется диалоговое окно Zoom (Масштаб) управления масштабом (рис. 1.14), в котором можно выбрать один из переключателей с желаемым значением масштаба Для задания значения вручную выберите переключатель Custom (Настройка) и в открывшемся текстовом поле введите нужное число (в процентах от реального масштаба страницы) Для подтверждения проделанных изменений нажмите кнопку ОК.
Начинаем работу
ГЛАВА 1. Начинаем работуИспользование панели инструментов Math
Использование панели инструментов Math
Если вы только начинаете осваивать редактор Mathcad, настоятельно рекомендую, где это только возможно, вводить формулы, пользуясь наборными панелями инструментов и описанной процедурой вставки функций с помощью диалога Insert Function (Вставить функцию). Это позволит избежать многих возможных ошибок.
Описанные действия демонстрируют использование Mathcad в качестве обычного калькулятора с расширенным набором функций. Для математика же интерес представляет, как минимум, возможность задания переменных и операций с функциями пользователя. Нет ничего проще — в Mathcad эти действия, как и большинство других, реализованы по принципу "как принято в математике, так и вводится". Поэтому приведем соответствующие примеры (листинги 1.2 и 1.3), не теряя времени на комментарии (если у вас возникнут проблемы с пониманием листингов, обратитесь за разъяснением к соответствующим разделам этой главы). Обратите внимание только на оператор присваивания, который применяется для задания значений переменным в первой строке листинга 1.2. Его, как и все остальные символы, можно ввести с помощью панели Calculator. Присваивание обозначается символом ":=" , чтобы подчеркнуть его отличие от операции вычисления.
Изменение масштаба
Изменение масштабаИзменение масштаба документа не влияет на его содержание, а просто определяет размер букв и графики, отображаемых на экране.
Для того чтобы изменить масштаб изображения, войдите в соответствующее поле на панели инструментов Standard, которое отмечено указателем мыши на рис. 1.13. Щелчок мыши на этом поле приводит к появлению списка возможных масштабов от 25 до 200%. Значение 100% соответствует размеру страницы документа, который получится при его распечатке. Сравните рис. 1.13 и 1.14, на которых один и тот же документ представлен при разном увеличении.
Изменение масштаба отображения документа
Изменение масштаба отображения документа
При дальнейшем перемещении курсора внутри региона линии ввода смещаются на один символ в соответствующую сторону. При выходе за пределы региона курсор снова становится курсором ввода в виде красного крестика.
Конечно, переместить курсор можно и щелчком мыши в соответствующем месте. Если щелкнуть на пустом месте, то в нем появится курсор ввода, а если в пределах региона — то линии ввода.
Изменение расположения и размера панелей инструментов
Изменение расположения и размера панелей инструментов
Имеется также и более простой способ открепить панель от границ окна Mathcad. Для этого просто щелкните дважды на ее первом или последнем разделителе. Чтобы прикрепить панель к окну, достаточно двойного щелчка на ее заголовке.
Перемещение панелей по экрану
Чтобы перемещать панели инструментов по экрану, необходимо предварительно сделать их плавающими. Плавающую панель легко поместить в любое место экрана ее перетаскиванием
Переместить панель в любое место экрана можно, даже если основное окно Mathcad не развернуто во весь экран, а занимает только его часть
Прикрепленные панели перемещайте вдоль границ окна, буксируя их мышью за крайние разделители. Таким способом удобно располагать несколько панелей инструментов в одну вертикальную или горизонтальную строку.
Чтобы изменить форму плавающей панели, т. е. выстроить кнопки на ней в другое соотношение рядов и столбцов, поместите указатель мыши на границу панели и, когда он приобретет характерную форму (рис. 1.9), нажмите левую кнопку мыши и перетащите при нажатой кнопке указатель, ориентируясь на изменяющуюся форму контура панели. Когда вы отпустите кнопку мыши, размеры панели изменятся.
Настройка состава основных панелей
Настройка означает изменение количества и состава кнопок на любой из трех основных панелей (Standard, Formatting и Mathematics). Она, например, полезна, если требуется убрать редко используемые кнопки, чтобы не загромождать экран (в особенности, если его невысокое разрешение вынуждает пользователя экономить место). Для изменения состава кнопок на панели вызовите щелчком правой кнопкой мыши в любом ее месте (но не на заголовке) контекстное меню и выберите в нем пункт Customize (Настроить). Появится диалоговое окно Customize Toolbar (Настройка панели инструментов), в котором имеются два списка — в левом перечислены отсутствующие кнопки, а в правом — кнопки, которые присутствуют в данный момент на панели (рис. 1.10).
Контекстное меню
Контекстное меню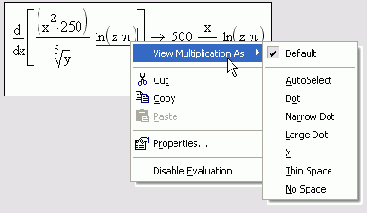
Курсор ввода
Курсор вводаНа некоторых рисунках этой главы (см., например, рис. 1.7) виден курсор ввода в виде небольшого крестика (на дисплее он имеет красный цвет). С его помощью отмечается незаполненное место в документе, куда в текущий момент можно вводить формулы или текст. Чтобы переместить курсор, достаточно щелкнуть указателем мыши в требуемом месте, либо передвинуть его клавишами-стрелками. Если выполнить щелчок в области формулы или начать ввод выражения на пустом месте, вместо курсора появятся линии редактирования, отмечающие место в формуле или тексте, редактируемым в данный момент (см. рис. 1.3 и 1.4).
Применение курсора ввода и приемов редактирования документов будет подробно рассмотрено в главе 2.
Листинги представляют собой фрагменты...
Листинги представляют собой фрагменты рабочих областей документа, которые работают без какого-либо дополнительного кода (если это не оговорено особо). Можно ввести содержание любого листинга в новый (пустой) документ, и он будет работать точно так же, как в книге. Чтобы не загромождать листинги, графики выведены в отдельные рисунки. В отличие от рис. 1.4, в следующих рисунках код листингов не дублируется, а если имеется ссылка на листинг в подрисуночной надписи, то это подразумевает, что данный график может быть вставлен в документ после упомянутого листинга.Одной из самых впечатляющих возможностей Mathcad являются символьные вычисления, позволяющие решить многие задачи аналитически. Фактически, по мнению автора, Mathcad "знает" математику, по крайней мере, на уровне неплохого ученого. Умелое использование интеллекта символьного процессора Mathcad избавит вас от огромного количества рутинных вычислений, к примеру, интегралов и производных (листинг 1.4). Обратите внимание на традиционную форму написания выражений, единственная особенность заключается в необходимости применения символа символьных вычислений -> вместо знака равенства. Его, кстати, можно ввести в редакторе Mathcad с любой из панелей Evaluation (Выражения) или Symbolic (Символика), а символы интегрирования и дифференцирования — с панели Calculus (Вычисления).
Расчет простого выражая
Листинг 1.1.Расчет простого выражаяИспользование переменных в расчетах
Листинг 1.2. Использование переменных в расчетахи рассчет ее значения
Листинг 1.3. Определение функции пользователя и рассчет ее значения в точке х=1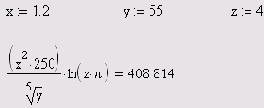
Символьные вычисления
Листинг 1.4. Символьные вычисления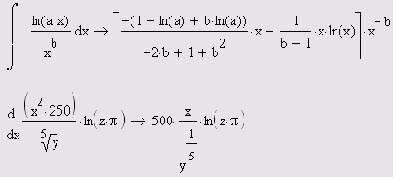
В этом разделе была рассмотрена лишь небольшая часть вычислительных возможностей системы Mathcad. Тем не менее, несколько приведенных здесь примеров дают неплохое представление о его назначении. Возможно даже, что преждевременно рассказав о простоте, с которой можно проводить математические расчеты, автор потерял некоторую часть самых нетерпеливых читателей, которые уже перешли к решению своих задач. Им я хочу посоветовать воспользоваться в качестве справочника второй и третьей частями книги, а для наилучшего оформления результатов — четвертой частью. Ниже, в этой и последующих главах данной части основы Mathcad освещены более подробно.
Математические панели инструментов
Математические панели инструментов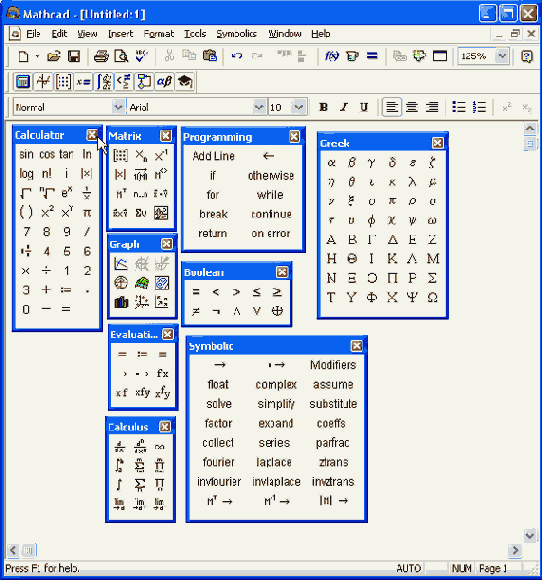
При наведении указателя мыши на многие из кнопок математических панелей появляется всплывающая подсказка, содержащая еще и сочетание "горя-чих клавиш", нажатие которых приведет к эквивалентному действию.
Меню Help
Меню Help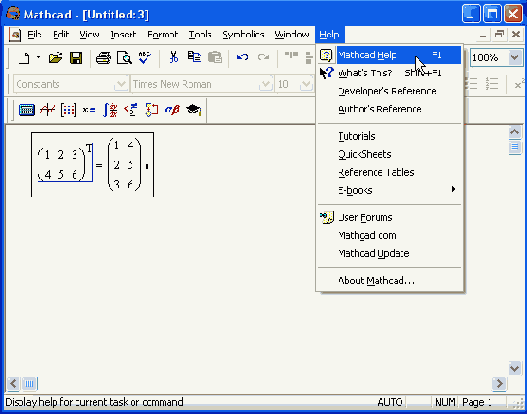
Если в какой-либо момент работы с Mathcad вам потребовалась помощь, выберите Help / Mathcad Help, либо нажмите клавишу
Справка в Mathcad является контекстно-зависимой, т е ее содержание определяется тем, на каком месте документа она вызвана Например, на рис. 1.19 курсор (линии ввода) указывает в редактируемом документе на оператор транспонирования матрицы Поэтому вызов справки приведет к загрузке окна Mathcad Help (Справка Mathcad), открытого на месте описания операции транспонирования матриц (рис. 1.20)
Окно справочной системы Mathcad построено в характерном для Windows стиле и состоит из двух частей Слева отображается содержание статей (вкладка Contents), а справа — их текст Левая часть окна может быть временно скрыта нажагием кнопки Hide на панели инструментов в верхней части окна Вновь вызвать ее на экран всегда можно кнопкой Show (Показать), заменяющей кнопку Hide в режиме скрытия содержания
Многооконный режим редактирования
Многооконный режим редактированияВсе предыдущие рисунки были примерами одного документа, развернутого во все пространство окна Mathcad. Однако допускается одновременно держать на экране и редактировать сразу несколько документов. Их можно расположить на экране в любом порядке. Для этого, открыв меню Window (Окно), следует выбрать в нем один из пунктов Cascade (Расположить каскадом), Tile Horizontal (Горизонтальная мозаика), Tile Vertical (Вертикальная мозаика). В результате все окна будут расположены на экране в пределах окна либо каскадом друг за другом, либо вертикально или горизонтально так, чтобы они не перекрывались (рис. 1.15—1.17).
Начинаем работу
Начинаем работуВ данной главе рассмотрено назначение приложения Mathcad 11 и, в целях знакомства с его основными возможностями, приведены базовые приемы его использования (см. разд. 1.1—1.2). Если вы уже имели дело с прежними версиями, начиная с Mathcad 7, и у вас неплохие навыки работы с его редактором, то можете смело пропустить эту главу. В ней основное внимание уделено главным компонентам интерфейса Mathcad 11, который интуитивен и похож на другие программы Windows (см. разд. 1.3), а также эффективному использованию справочной системы Mathcad (см. разд. 1.4).
Настройка состава панели инструментов
Настройка состава панели инструментов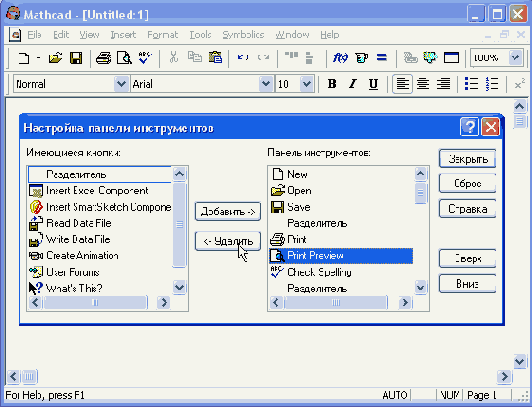
Чтобы убрать кнопку (или разделитель кнопок) с панели инструментов, выделите ее имя в правом списке и затем нажмите кнопку Remove (Удалить) в диалоговом окне (на нее наведен указатель мыши на рис. 1.10). Чтобы добавить новую кнопку, выделите ее имя в левом списке и нажмите Add (Добавить). Для изменения порядка расположения на панели той или иной кнопки выделите ее в правом списке и перемещайте в нужную сторону, нажимая кнопки Move Up (Вверх) или Move Down (Вниз).
Подтвердить сделанную настройку панели можно нажатием кнопки Close (Закрыть) или кнопки закрытия диалогового окна, а вернуться к прежнему составу панели — с помощью кнопки Reset (Сброс).
Окно Mathcad 11 с новым документом
Окно Mathcad 11 с новым документом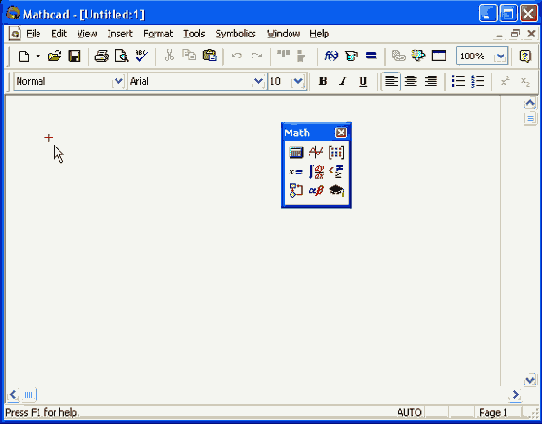
После того как Mathcad 11 установлен на компьютере и запущен на исполнение, появляется основное окно приложения, показанное на рис. 1.1. Оно имеет ту же структуру, что и большинство приложений Windows. Сверху вниз располагаются заголовок окна, строка меню, панели инструментов (стандартная и форматирования) и рабочий лист или рабочая область документа (worksheet). Новый документ создается автоматически при запуске Mathcad. В самой нижней части окна находится строка состояния. Не забывая о сходстве редактора Mathcad с обычными текстовыми редакторами, вы интуитивно поймете назначение большинства кнопок на панелях инструментов.
Помимо элементов управления, характерных для типичного текстового редактора, Mathcad снабжен дополнительными средствами для ввода и редактирования математических символов, одним из которых является панель инструментов Math (Математика) (рис. 1.1). С помощью этой, а также ряда вспомогательных наборных панелей, удобно осуществлять ввод уравнений.
Для того чтобы выполнить простые расчеты по формулам, проделайте следующее:
Окно справочной системы Mathcad
Окно справочной системы Mathcad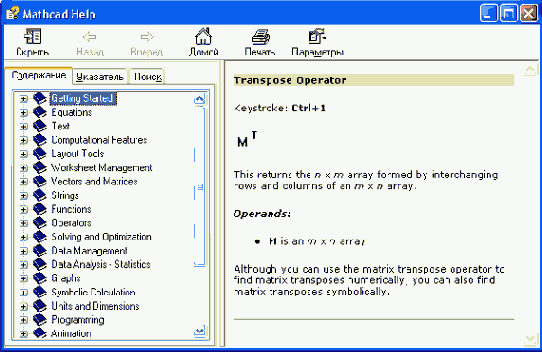
Справочная система построена по принципу гиперссылок, находящихся в тексте статей и обеспечивающих переход от одной статьи к другой Текст статьи загружается в правую часть окна Для возвращения на однажды просмотренные страницы предусмотрены кнопки навигации Back (Назад), Forward (Вперед) и Ноте (Домой).
В тексте статей часто встречаются кнопки QuickSheet Example (Пример из шпаргалок), вызывающие образец из Ресурсов Mathcad, связанный с содержанием справочной статьи Нажатие такой кнопки приведет к появлению окна Mathcad Resource с примером расчетов, относящихся к теме раздела справочной системы.
В левой части окна на вкладке Contents (Содержание) изначально перечислены только основные главы справочной системы, снабженные значком в виде закрытой книжки Подзаголовки раскрываются с помощью двойного щелчка на названии нужной главы При этом значок меняется на раскрытую книжку, а подзаголовки выводятся в сопровождении значков в виде вопросительного знака Щелчок на любом из подзаголовков выводит соответствующую статью справки справа.
Статей гораздо больше, чем подзаголовков в содержании, для вывода большинства из них на экран потребуется один-два перехода по гиперссылкам Кроме того, довольно мощное средство поиска статей на сходную тему — это кнопка Related Topics (Близкие статьи). Нажатие этой кнопки раскрывает диалоговое окно Topics Found (Найденные статьи) с перечнем справочных статей близкой тематики (рис. 1.21) Чтобы перейти к какой-либо статье, выберите соответствующий элемент из списка и нажмите кнопку Display (Показать) или просто дважды щелкните на элементе списка.
Окно с термином на фоне справочной статьи
Окно с термином на фоне справочной статьи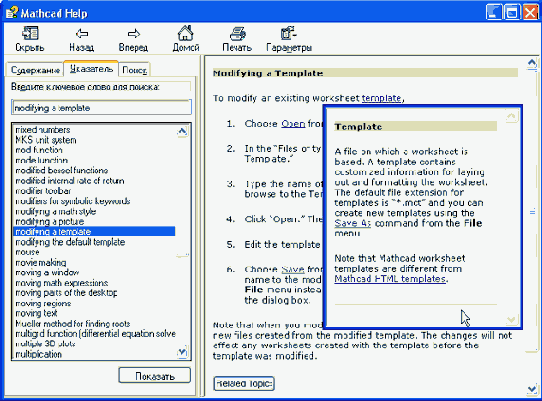
В левой части окна Mathcad Help (Справка Mathcad) отображается содержимое одной из трех закладок:
Основные панели инструментов
Основные панели инструментов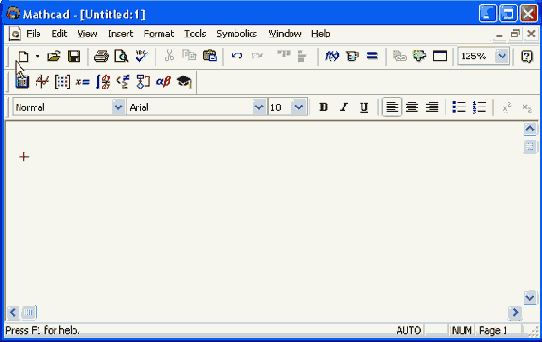
Панель Math предназначена для вызова на экран еще девяти панелей (рис. 1.8), с помощью которых, собственно, и происходит вставка математических операций в документы В прежних версиях Mathcad эти математические панели инструментов назывались палитрами (palettes) или наборными панелями. Чтобы показать какую-либо из них, нужно нажать соответствующую кнопку на панели Math (см. рис. 1.3) Перечислим назначение математических панелей:
Перемещение по документу
Перемещение по документуПросматривать документ вверх-вниз и вправо-влево удобно с помощью вертикальной и горизонтальной полос прокрутки, перемещая их бегунки (в этом случае обеспечивается плавное перемещение вдоль документа) или щелкая мышью с одной из двух сторон бегунка (при этом перемещение по документу будет скачкообразным). Также для перемещения курсора по документу можно использовать клавиши листания страниц
Для того чтобы двигаться по документу вверх-вниз и вправо-влево, перемещая курсор, следует нажимать на соответствующие клавиши управления курсором. Попадая в область регионов с формулами и текстом, курсор превращается в две линии ввода — вертикальную и горизонтальную синего цвета.
Поиск близких по смыслу справочных статей.
Поиск близких по смыслу справочных статей.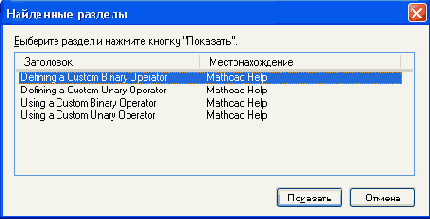
Некоторые гиперссылки приводят не к переходу на другую страницу справочной системы, а выводят окно с термином (рис. 1.22) Для того чтобы после ознакомления убрать это окно, достаточно щелкнуть в его пределах мышью
Поиск справочных статей по ключевым словам
Поиск справочных статей по ключевым словам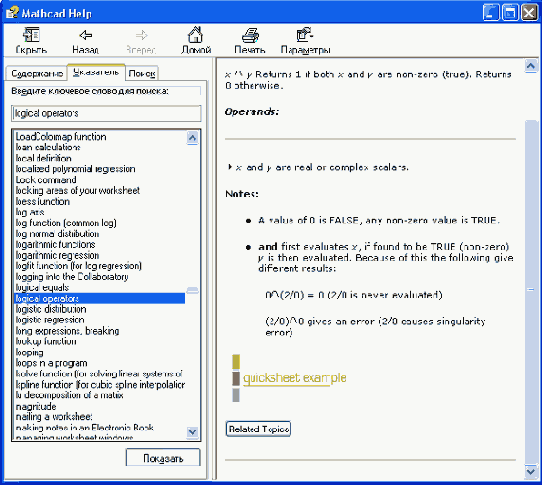
В заключение отметим, что как справочная система, так и Ресурсы Mathcad представляют собой не просто статьи и примеры с описанием его возможностей. Они могут быть названы полноправными учебными пособиями по нескольким курсам высшей математики (в случае Ресурсов, к тому же, еще и интерактивными). Там освещены основные определения, математический смысл многих операций и алгоритмы численных методов Причем, на взгляд автора, некоторые из тем объяснены лучше, чем где бы то ни было. Если Вы в достаточной степени владеете английским, обязательно ознакомьтесь с Ресурсами Mathcad.
Построение графика функции (листинг 1.3)
Построение графика функции (листинг 1.3)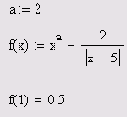
Сравните содержание листинга 1.3 и рис. 1 4. Такой стиль подачи материала будет сохранен во всей книге.
Работа с меню
Работа с меню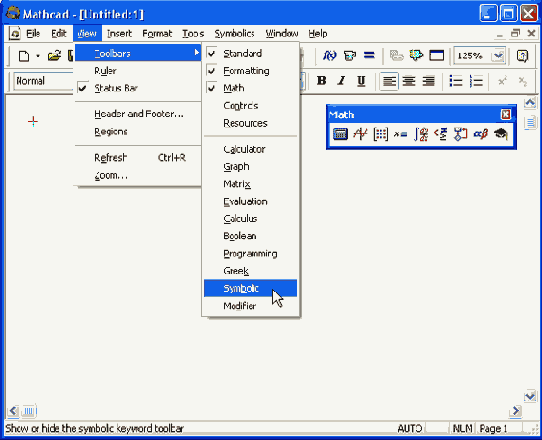
Обратите внимание, что пункты меню, которые содержат подменю, снабжены стрелками (как пункт Toolbars на рис. 1.5). Кроме того, некоторые пункты меню имеют (или не имеют) флажки проверки, указывающие на включение (или выключение) соответствующей опции в текущий момент. Так, на рис. 1.5 флажки проверки выставлены в пунктах Status Bar (Строка состояния) и имен трех панелей инструментов, что говорит о наличии в данный момент на экране строки состояния и трех панелей. Флажки же в пунктах Ruler (Линейка), Regions (Регионы) и имен математических панелей инструментов отсутствуют, т. е. в данный момент эти опции выключены
Назначение пунктов меню, на которые наведен указатель мыши, появляется в виде подсказки слева на строке состояния (в нижней части окна Mathcad). На рис. 1.5 указатель наведен на пункт Symbolic, поэтому подсказка гласит "Show or hide the symbolic keyword toolbar" (Показать или скрыть панель символики).
Помимо верхнего меню, схожие функции выполняют всплывающие меню (рис. 1.6). Они появляются, как и в большинстве других приложений Windows, при нажатии в каком-либо месте документа правой кнопки мыши. При этом состав данных меню зависит от места их вызова, поэтому их еще называют контекстными. Mathcad сам "догадывается", в зависимости от контекста, какие операции могут потребоваться в текущий момент, и помещает в меню соответствующие команды. Поэтому использовать контекстное меню зачастую проще, чем верхнее, т. к. не надо вспоминать, где конкретно в верхнем меню находится нужный пункт. Как и верхнее меню, контекстное также может иметь подменю (на рис. 1.6 показан участок документа с примером изменения отображения знака умножения в формуле; примечательно, что эту операцию в Mathcad можно осуществить только при помощи контекстного меню).
Расположение документов каскадом
Расположение документов каскадом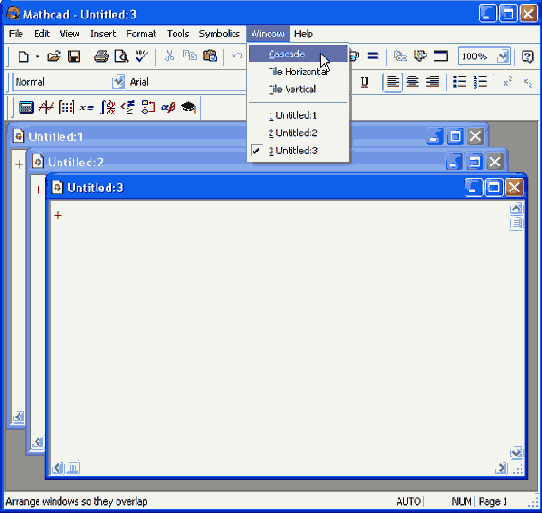
Обратите внимание, что в окне каждого документа расположен свой курсор (курсор ввода или линии редактирования, в зависимости от места в документе). Кроме того, для каждого документа легко включить либо отключить линейку, задать свой масштаб (как это сделано на рис. 1.17) или установить опцию отображения границ регионов. В каждый момент времени допускается редактирование только одного документа Заголовок окна активного документа выделен более ярким цветом. Окно документа активизируется либо щелчком мыши в его пределах, либо выбором его имени в выпадающем меню Window (Окно). Имена открытых документов расположены в нижней части меню Window, а имя активного документа отмечено флажком.
Расположив несколько документов на экране, можно менять положение и размер каждого из них, перетаскивая их окна за заголовок и перетаскивая линии их границ.
Расположение документов по горизонтали
Расположение документов по горизонтали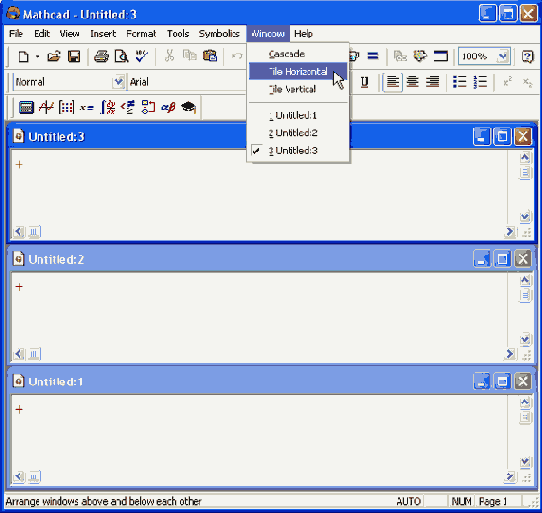
В многооконном режиме удобно копировать объекты из одного документа в другой с помощью техники перетаскивания (Drag-and-Drop) Для этого достаточно ухватить объект указателем, используя левую кнопку мыши, за его границу и буксировать его в окно другого документа, не отпуская кнопку мыши (см рис 1 17)
Расположение документов по вертикали
Расположение документов по вертикали
В многооконном режиме любой документ можно закрыть или развернуть во весь экран с помощью кнопок управления окном в его правом верхнем углу. Когда окно документа развернуто, кнопки управления его окном помещаются в область верхнего меню, а переход между различными документами осуществляется только через меню Window (Окно)
Строка состояния
Строка состояния
Чтобы показать или скрыть строку состояния, выполните команду View / Status Ваг (Вид / Строка состояния).
Указатель справочных статей
Указатель справочных статей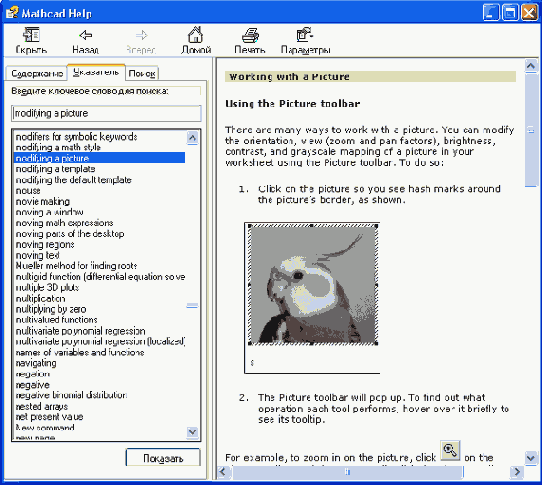
На вкладке index следует либо выбрать искомую статью из нижнего списка, либо ввести несколько первых букв в текстовое поле 'type in the keyword to find (Введите ключевое слою для поиска). Для перехода к содержимому справки требуется дважды щелкнуть на элементе списка. После этого либо статья появится справа, либо будет выведено уже известное нам диалоговое окно Topics Found (Найденные статьи), позволяющее выбрать справочную статью из списка.
Если название искомой статьи известно точно, перейдите на вкладку index, если же требуется отыскать справку по ключевым словам, выполните поиск по ключевому слову (рис. 1.24).
Вид документа с выделенными границами регионов
Вид документа с выделенными границами регионов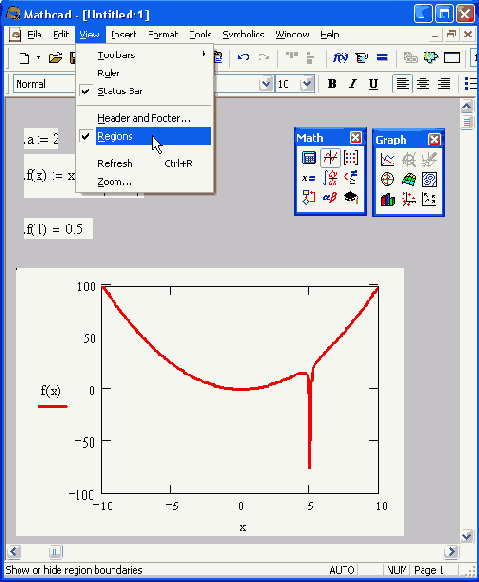
Ориентироваться в размещении объектов на странице документа помогает горизонтальная линейка, расположенная под панелями инструментов в верхней части окна Mathcad (рис. 1.12) Линейку можно вызвать на экран с помощью команды View / Ruler (Вид / Линейка)
Внешний вид документа
Внешний вид документаДокумент Mathcad строится по принципу размещения формул и текста в рабочей области, которая изначально является подобием чистого листа. Чтобы показать или скрыть расположение регионов с математическими выражениями, текстом или графиками, имеется возможность включить опцию показа границ регионов. Делается это с помощью главного меню View / Regions (Вид / Регионы). Если эта опция включена, документ выглядит так, как показано на рис. 1.11 (см. рис. 1.4 для сравнения).
Присмотревшись к рис. 1.11 и некоторым другим рисункам этой главы, вы обнаружите в правой части рабочей области вертикальную линию раздела страниц. Если документ большой, то в некотором месте будет наблюдаться и прерывистая горизонтальная линия раздела страниц. Эти линии показывают, каким образом будет осуществлено разбиение на страницы при распечатке документа на принтере. Изменить параметры страницы можно с помощью команды File / Page Setup (Файл / Параметры страницы).
Вставка встроенной функции
Вставка встроенной функции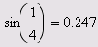
Подробнее о назначении этих и других наборных панелей инструментов рассказано ниже (см. разд. 1.3).
К примеру, можно ввести выражение из листинга 1.1 исключительно с помощью панели Calculator. Для этого нужно сначала нажать кнопку sin (самую первую сверху). Результат данного действия показан на рис. 1.3 (выражение в рамке). Теперь остается лишь набрать выражение 1/4 внутри скобок (в местозаполнителе, обозначаемом черным прямоугольником). Для этого нажмите последовательно кнопки 1, — и 4 на панели Calculator и затем, на ней же, кнопку —, чтобы получить ответ (разумеется, тот же самый, что и в предыдущей строке документа).
Как видите, вставлять в документы математические символы можно по-разному, как и во многих других приложениях Windows. В зависимости от опыта работы с Mathcad и привычек работы на компьютере, пользователь может выбрать любой из них.
Вызов линейки
Вызов линейки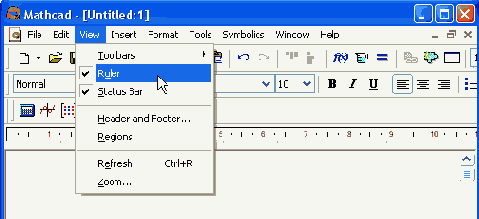
Математический редактор MathCAD
Функции преобразования координат (Vector and Matrix)
10.10. Функции преобразования координат (Vector and Matrix)В Mathcad 2001 появилось семейство новых функций, позволяющих перейти от одних координат к другим, как на плоскости, так и в пространстве:
Финансовые функции (Finance)
10.11. Финансовые функции (Finance)Начиная с версии 2000, в Mathcad появились функции, облегчающие финансовый анализ. приведем список этих функций, не вдаваясь в пояснения и надеясь на то, что заинтересованнvй читатель найдет подробное описание и практические примерv их применения в справочной системе Mathcad.
Обычные функции Бесселя
10.1.1. Обычные функции БесселяФункции Бесселя первого и второго рода обычно возникают как решения волнового уравнения с цилиндрическими граничными условиями.
Конкретный вид соответствующих дифференциальных уравнений можно без труда отыскать в справочниках по спецфункциям или в справочной системе Mathcad.
Модифицированные функции Бесселя
10.1.2. Модифицированные функции БесселяПеречислим их:
Функции Эйри
10.1.3. Функции ЭйриФункции Эйри являются независимыми решениями ОДУ y' '=zy. Их вид показан на рис. 10.5. Итак:
Функции Бесселя-Кельвина
10.1.4. Функции Бесселя-КельвинаКомплексная комбинация функций Бесселя-Кельвина вида ber(n,x) + i bei(n,x) является решением соответствующего ОДУ, зависящего от параметра n. Вид графиков функции bei для n=i и 2 показан на рис. 10.6.
Сферические функции Бесселя
10.1.5. Сферические функции БесселяГрафик сферических функций Бесселя первого порядка показан на рис. 10.7.
Функции Бесселя (Bessel)
10.1. Функции Бесселя (Bessel)Функции Бесселя, по определению, являются решениями различных краевых задач для некоторых обыкновенных дифференциальных уравнений (ОДУ).
Функции работы с комплексными числами (Complex Numbers)
10.2. Функции работы с комплексными числами (Complex Numbers)В Mathcad имеется несколько функций, облегчающих работу с комплексными числами.
Логарифмы и экспонента (Log and Exponential)
10.3. Логарифмы и экспонента (Log and Exponential)Перечислим без комментариев хорошо известные логарифмические функции (рис. 10.8) и экспоненциальную функцию:
Тригонометрические функции (Trigonometric)
10.4. Тригонометрические функции (Trigonometric)Гиперболические функции (Hyperbolic)
10.5. Гиперболические функции (Hyperbolic)Гиперболические функции, согласно определению, выражаются через различные комбинации ez и е~г (пример приведен в листинге 10.7). Аргумент гиперболических функций также может быть комплексным. Графики трех основных гиперболических функций показаны на рис. 10.9.
Другие спецфункции (Special)
10.6. Другие спецфункции (Special)Приведем перечень остальных спецфункций, которые рассчитываются Mathcad встроенным образом. Действие некоторых функций иллюстрируется листингом 10.8, а некоторые полиномы — графиками на рис. 10.11—10.13.
Строковые функции (String)
10.7. Строковые функции (String)Приведем перечень функций, благодаря которым пользователь может оперировать со строковыми переменными, подобно операциям с числами:
Функции сокращения и округления (Truncation and Round-Off)
10.8. Функции сокращения и округления (Truncation and Round-Off)Кусочно-непрерывные функции (Piecewise Continuous)
10.9. Кусочно-непрерывные функции (Piecewise Continuous)Функции Бесселя-Кельвина
Функции Бесселя-Кельвина
Функции Бесселя первого рода
Функции Бесселя первого рода
Функции Бесселя второго рода
Функции Бесселя второго рода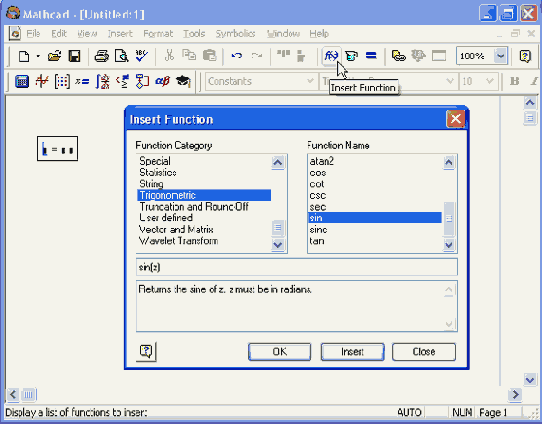
Функции Эйри
Функции Эйри
Функции Кронекера и Хевисайда
Функции Кронекера и Хевисайда
Использование функции создания сообщения об ошибке
Использование функции создания сообщения об ошибке
Функции взаимных преобразований чисел и строк
Листинг 10.10. Функции взаимных преобразований чисел и строк
Округление чисел
Листинг 10.12. Округление чисел

При округлении не забывайте о принципах представления чисел в Mathcad. Чтобы отобразить нужное количество знаков после десятичной точки, воспользуйтесь диалогом Result Format (Формат результата) (см. гл. 4).
Функции преобразования координат в пространстве
Листинг 10.15. Функции преобразования координат в пространстве

Пример действия функции csgn
Листинг 10.2. Пример действия функции csgn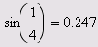
Пример действия функции signum
Листинг 10.3. Пример действия функции signum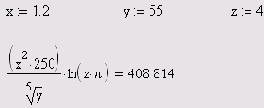
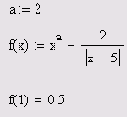
Примеры расчета угла между прямой и осью OX
Листинг 10.5. Примеры расчета угла между прямой и осью OX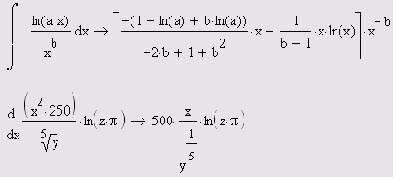
Расчет тригонометрических функций в градусах
Листинг 10.6. Расчет тригонометрических функций в градусах

Пример гиперболических функций
Листинг 10.7. Пример гиперболических функций
Логарифмические функции
Логарифмические функции
Модифицированные функции Бесселя первого рода
Модифицированные функции Бесселя первого рода
Примеры нескольких первых модифицированных функций Бесселя показаны на рис. 10.3 и 10.4.
Модифицированные функции Бесселя второго рода
Модифицированные функции Бесселя второго рода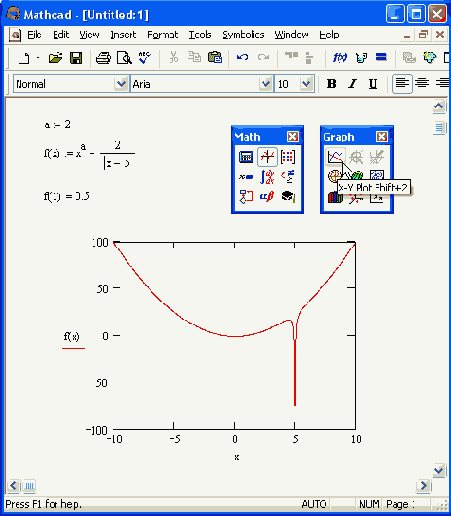
Основные гиперболические функции
Основные гиперболические функции
Полиномы Чебышева
Полиномы Чебышева
Полиномы Эрмита
Полиномы Эрмита
Полиномы Лаггера
Полиномы Лаггера
Полиномы Лежандра
Полиномы Лежандра
Сферические функции Бесселя первого порядка
Сферические функции Бесселя первого порядка
Математический редактор MathCAD
Вычислительный блок Given/Odesolve
11.1.1. Вычислительный блок Given/OdesolveВычислительный блок для решения одного ОДУ, реализующий численный метод Рунге-Кутты, состоит из трех частей:
Пример решения задачи Коши для ОДУ первого порядка у' =у-у2 посредством вычислительного блока приведен в листинге 11.1.
Встроенные функции rkfixed, Rkadapt, Bulstoer
11.1.2. Встроенные функции rkfixed, Rkadapt, BulstoerАльтернативный метод решения ОДУ перешел из прежних версий Mathcad. Он заключается в использовании одной из встроенных функций rkfixed, Rkadapt или Bulstoer. Этот способ несколько проигрывает первому и в простоте, и в наглядности Поэтому я советую предпочесть вычислительный блок Given/odesoive Однако иногда приходится решать ОДУ первого порядка с помощью второго способа, например, при следующих обстоятельствах:
ОДУ первого порядка
11.1. ОДУ первого порядкаДифференциальное уравнение первого порядка может по определению содержать, помимо самой искомой функции у (t), только ее первую производную y'(t). В подавляющем большинстве случаев дифференциальное уравнение можно записать в стандартной форме (форме Коши):
у (t)=f(y(t),t), (1)
и только с такой формой умеет работать вычислительный процессор Mathcad. Правильная с математической точки зрения постановка соответствующей задачи Коши для ОДУ первого порядка должна, помимо самого уравнения, содержать одно начальное условие — значение функции y(t0) в некоторой точке t0. Требуется явно определить функцию y(t) на интервале от t0 до tx. По характеру постановки задачи Коши называют еще задачами с начальными условиями (initial value problem), в отличие от краевых задач.
Для численного интегрирования одного ОДУ у пользователя Mathcad 11 (начиная с версии Mathcad 2000 Pro) имеется выбор — либо использовать вычислительный блок Given/odesoive, либо встроенные функции, как в прежних версиях Mathcad. Первый путь предпочтительнее из соображений наглядности представления задачи и результатов, а второй дает пользователю больше рычагов воздействия на параметры численного метода. Рассмотрим последовательно оба варианта решения.
ОДУ высшего порядка
11.2. ОДУ высшего порядкаОбыкновенное дифференциальное уравнение с неизвестной функцией y(t), в которое входят производные этой функции вплоть до y(N) (t), называется ОДУ N-ГО порядка. Если имеется такое уравнение, то для корректной постановки задачи Коши требуется задать N начальных условий на саму функцию y(t) и ее производные от первого до (N-1) го порядка включительно. В Mathcad 11 можно решать ОДУ высших порядков как с помощью вычислительного блока Given/odesolve, так и путем сведения их к системам уравнений первого порядка.
Внутри вычислительного блока:
Встроенные функции для решения систем ОДУ
11.3.1. Встроенные функции для решения систем ОДУВ Mathcad 11 имеются три встроенные функции, которые позволяют решать поставленную в форме (2—3) задачу Коши различными численными методами.
Каждая из приведенных функций выдает решение в виде матрицы размера (M+1)х(N+1). В ее левом столбце находятся значения аргумента t, делящие интервал на равномерные шаги, а в остальных N столбцах — значения искомых функций y0(t) ,y1(t), .. ,yN-1(t), рассчитанные для этих значений аргумента Поскольку всего точек (помимо начальной) м, то строк в матрице решения будет всего M+1
В подавляющем большинстве случаев достаточно использовать первую функцию rkfixed, как это показано в листинге 11.4 на примере решения системы ОДУ модели осциллятора с затуханием (см. разд. 11 2).
Решение систем ОДУ в одной заданной точке
11.3.2. Решение систем ОДУ в одной заданной точкеЗачастую при решении дифференциальных уравнений требуется определить значения искомых функций не на всем интервале (to,ti), а только в одной его последней точке. Например, весьма распространены задачи поиска аттракторов динамических систем. Известно, что для широкого класса ОДУ одна и та же система при разных (или даже любых, как рассмотренный выше пример осциллятора с затуханием) начальных условиях приходит в одну и ту же точку (аттрактор). Поэтому часто нужно определить именно эту точку.
Такая задача требует меньше ресурсов компьютера, чем решение системы ОДУ на всем интервале, поэтому в Mathcad имеются модификации встроенных функций rkadapt и Bulstoer. Они имеют несколько другой набор параметров и работают быстрее своих аналогов.
Пример использования функции buistoer для того же примера (11.2—1) приведен в листинге 11.5. В его первых двух строках, как обычно, определяется система уравнений и начальные условия; в следующей строке матрице и присваивается решение, полученное с помощью buistoer. Структура этой матрицы в точности такая же, как и в случае решения системы ОДУ посредством уже рассмотренных нами ранее встроенных
функций (см. разд. 11.3.1). Однако в данном случае нам интересна только последняя точка интервала. Поскольку сделанное численным методом количество шагов, т. е. размер матрицы и, заранее неизвестно, то его необходимо предварительно определить. Это сделано в четвертой строке листинга, присваивающей это число переменной м, в этой же строке оно выведено на экран. В предпоследней строке листинга осуществлен вывод решения системы ОДУ на конце интервала, т. е. в точке t=s0 в виде вектора. В последней строке для примера еще раз выводится искомое значение первой функции из системы ОДУ (сравните его с соответствующим местом вектора из предыдущей строки).
Некоторые примеры
11.3.3. Некоторые примерыВ предыдущих разделах были использованы примеры исключительно линейных уравнений, т. е. содержащих только первую степень неизвестных функций и их производных. Между тем, многие нелинейные уравнения демонстрируют совершенно удивительные свойства, причем решение большинства из них можно получить лишь численно. Рассмотрим несколько наиболее известных классических примеров систем ОДУ, имея в виду, что читателю они могут пригодиться как в познавательных, так и в практических целях. Это модели динамики популяций (Вольтерры), генератора автоколебаний (Ван дер Поля), турбулентной конвекции (Лоренца) и химической реакции с диффузией (Пригожина). Все они (впрочем, как и уже приведенные выше в этой главе) содержат производные по времени t и описывают динамику различных физических параметров. Задачи Коши для таких моделей называют динамическими системами, и для их изучения центральным моментом является анализ фазовых портретов, т. е. решений, получающихся при выборе всевозможных начальных условий.
В большинстве примеров, изложенных ниже, для построения фазового портрета рассчитывается несколько решений для разных начальных условий.
Ограничимся в дальнейшем минимальными комментариями и приведем листинги и графики решений без подробного обсуждения.
Системы ОДУ первого порядка
11.3. Системы ОДУ первого порядкаMathcad требует, чтобы система дифференциальных уравнений была представлена в стандартной форме.
Задание системы эквивалентно следующему векторному представлению, где Y и У ' — соответствующие неизвестные векторные функции переменной t размера NXI, ар — векторная функция того же размера и (N+i) количества переменных (N компонент вектора и, возможно, t). Именно векторное представление используется для ввода системы ОДУ в среде Mathcad.
Для того чтобы определить задачу Коши для системы ОДУ, следует определить еще N начальных условий, задающих значение каждой из функций yi(t0) в начальной точке интегрирования системы t0. В векторной форме они могут быть записаны, где в — вектор начальных условий размера NXI, составленный из y1(t0).
Как Вы заметили, задача сформулирована для систем ОДУ первого порядка. Однако если в систему входят и уравнения высших порядков, то ее можно свести к системе большего числа уравнений первого порядка, подобно тому как это было сделано на примере уравнения осциллятора (см. разд. 11.2).
Обратите внимание на необходимость векторной записи как самого уравнения, так и начального условия. В случае одного ОДУ соответствующие векторы имеют только один элемент, а в случае системы N>I уравнений — N.
Фазовый портрет динамической системы
11.4. Фазовый портрет динамической системыДо сих пор в этой главе в качестве примеров расчета динамических систем мы приводили графики траекторий на фазовой плоскости. Однако для надежного исследования фазового портрета необходимо решить систему ОДУ большое количество раз с самыми разными начальными условиями (и, возможно, с разным набором параметров модели), чтобы посмотреть, к каким аттракторам сходятся различные траектории. В Mathcad можно реализовать эту задачу, например, в форме алгоритма, приведенного в листинге 11.10 для решения системы уравнений автокаталитической химической реакции с диффузией. Эта модель, называемая моделью брюсселятора, предложена в 1968 г. Лефевром и Пригожиным. Неизвестные функции отражают динамику концентрации промежуточных продуктов некоторой реальной химической реакции. Параметр модели в равен исходной концентрации катализатора.
Листании 11.10. Построение фазового портрета для модели брюсселятора

Предложенный алгоритм формирует из отдельных матриц решений системы ОДУ с разными начальными условиями объединенную матрицу и. Пары начальных условий задаются в первой строке листинга в виде матрицы v размера 2х10. Последнее означает построение десяти траекторий. Для того чтобы поменять количество траекторий, измените соответствующим образом размер этой матрицы. Затем (рис. 11.14) элементы матрицы и выводятся на график в виде отдельных точек. Отсутствие соединения точек линиями является недостатком алгоритма, но это плата за возможность представить в Mathcad несложным образом сразу большое количество траекторий на фазовой плоскости.

Что такое жесткие ОДУ?
11.5.1. Что такое жесткие ОДУ?Строгого общепринятого математического определения жестких ОДУ нет. В рамках этой книги будем считать, что жесткие системы — это те уравнения, решение которых получить намного проще с помощью определенных неявных методов, чем с помощью явных методов (типа тех, что были рассмотрены в предыдущих разделах). Примерно такое определение было предложено в 1950-х годах классиками в этой области Кертиссом и Хирш-фельдером. Начнем разговор о жестких ОДУ с примера нежесткого уравнения (листинг 11.11), решение которого показано на рис. 11.16. На том же графике показано решение подобного ОДУ с другим коэффициентом при правой части, равным не -10, а -30. Решение обоих уравнений не составило труда, и численный метод Рунге-Кутты дал правильный результат.
Листании 11.11. Решение нежесткого ОДУ


Функции для решения жестких ОДУ
11.5.2. Функции для решения жестких ОДУРешение жестких систем дифференциальных уравнений можно осуществить только с помощью встроенных функций, аналогичных по действию семейству рассмотренных выше функций для обычных ОДУ.
Покажем действие этих алгоритмов на том же примере жесткой системы ОДУ химической кинетики (листинг 11.14). Обратите внимание, как следует представлять в данном случае якобиан, сравнив задание матричной функции в предпоследней строке листинга 11.14 с заданием якобиана из листинга 11.13.
Жесткие системы ОДУ
11.5. Жесткие системы ОДУДо сих пор мы имели дело с "хорошими" уравнениями, которые надежно решались численными методами Рунге-Кутты. Однако имеется класс так называемых жестких (stiff) систем ОДУ, для которых стандартные методы практически неприменимы, поскольку их решение требует исключительно малого значения шага численного метода. Некоторые из специальных алгоритмов, разработанных для этих систем, реализованы в Mathcad.
Аттрактор Лоренца
Аттрактор ЛоренцаОдна из самых знаменитых динамических систем предложена в 1963 г. Лоренцем в качестве упрощенной модели конвективных турбулентных движений жидкости в нагреваемом сосуде тороидальной формы. Система состоит из трех ОДУ и имеет три параметра модели (листинг 11.9). Поскольку неизвестных функций три, то фазовый портрет системы должен определяться не на плоскости, а в трехмерном пространстве.
Аттрактор Лоренца (листинг 11.9)
Аттрактор Лоренца (листинг 11.9)Решением системы Лоренца при определенном сочетании параметров (рис. 11.12) является странный аттрактор (или аттрактор Лоренца) — притягивающее множество траекторий на фазовом пространстве, которое по виду идентично случайному процессу. В некотором смысле, аттрактор Лоренца является стохастическими автоколебаниями, которые поддерживаются в динамической системе за счет внешнего источника.
Решение в виде странного аттрактора появляется только при некоторых сочетаниях параметров. В качестве примера на рис. 11.13 приведен результат для г=ю и тех же значений остальных параметров. Как видно, аттрактором в этом случае является фокус. Перестройка типа фазового портрета происходит в области промежуточных г. Критическое сочетание параметров, при которых фазовый портрет системы качественно меняется, называется в теории динамических систем точкой бифуркации. Физический смысл бифуркации в модели Лоренца, согласно современным представлениям, описывает переход ламинарного движения жидкости к турбулентному.

Фазовый портрет брюсселятора при в=0.5 (листинг 11.10)
Фазовый портрет брюсселятора при в=0.5 (листинг 11.10)Как видно из рис. 11.14, все траектории, вышедшие из разных точек, асимптотически стремятся к одному и тому же аттрактору (1,0.5). Из теории динамических систем нам известно, что такой аттрактор называется узлом (с узлом мы уже встречались в примерах разд. 11.1). Конечно, в общем случае при анализе фазового портрета желательно "прощупать" большее число траекторий, задавая более широкий диапазон начальных условий. Не исключено, что в других областях фазовой плоскости траектории будут сходиться к другим аттракторам
Эволюцию фазового портрета брюсселятора можно наблюдать, проводя расчеты с различным параметром в. При его увеличении узел будет сначала постепенно смещаться в точку с координатами (1,в), пока не достигнет бифуркационного значения в=2. В этой точке происходит качественная перестройка портрета, выражающаяся в рождении предельного цикла. При дальнейшем увеличении в происходит лишь количественное изменение параметров этого цикла. Решение, полученное при в=2.5, показано на рис. 11.15.
Чтобы найти аттракторы динамической системы, как известно, нужно решить систему алгебраических уравнений, получающуюся из системы ОДУ заменой нулями их левых частей. Эти задачи также удобно решать средствами Mathcad (см. гл. 8). В частности, исследование зависимости фазового портрета от параметров системы ОДУ и поиск бифуркаций можно проводить методами продолжения (см. разд. "Метод продолжения по параметру" гл. 8).

с расчетом динамических систем, несомненно
Фазовый портрет брюсселятора при в=2.5Читатели, сталкивающиеся с расчетом динамических систем, несомненно оценят возможности Mathcad по построению фазовых портретов и исследованию бифуркаций. Возможно также, что они найдут лучшие программные решения этой задачи, чем алгоритм, предложенный в данном разделе автором.
Фазовый портрет, полученный bulstoer (слева) и rkadapt (справа) (листинг 11.5)
Фазовый портрет, полученный bulstoer (слева) и rkadapt (справа) (листинг 11.5)
Фазовый портрет решения системы ОДУ при M=100 (слева) и М=200 (справа) (листинг 11.4)
Фазовый портрет решения системы ОДУ при M=100 (слева) и М=200 (справа) (листинг 11.4)
В общем случае, если система состоит из N ОДУ, то фазовое пространство является N-мерным. При N>3 наглядность теряется, и для визуализации фазового портрета приходится строить его различные проекции.
На том же рис. 11.5, справа, показан для сравнения результат расчета фазового портрета с большим числом шагов. Видно, что в этом случае обеспечивается лучшая точность и, в результате, решение получается более гладким. Конечно, при этом увеличивается и время расчетов.
При решении систем ОДУ многие проблемы могут быть устранены при помощи простой попытки увеличить число шагов численного метода В частности, сделайте так при неожиданном возникновении ошибки "Found a number with a magnitude greater than 10^307" (Найдено число, превышающее значение 10307) Данная ошибка может означать не то, что решение в действительности расходится, а просто недостаток шагов для корректной работы численного алгоритма
В заключение следует сказать несколько слов об особенностях различных численных методов. Все они основаны на аппроксимации дифференциальных уравнений разностными аналогами. В зависимости от конкретной формы аппроксимации, получаются алгоритмы различной точности и быстродействия. В Mathcad использован наиболее популярный алгоритм Рунге-Кутты четвертого порядка, описанный в большинстве книг по методам вычислений. Он обеспечивает малую погрешность для широкого класса систем ОДУ за исключением жестких систем. Поэтому в большинстве случаев стоит применять функцию rkfixed. Если по различным причинам время расчетов становится критичным или точность неудовлетворительна, стоит попробовать вместо rkfixed другие функции, благо сделать это очень просто, благодаря одинаковому набору параметров. Для этого нужно только поменять имя функции в программе.
Функция Rkadapt может быть полезна в случае, когда известно, что решение на рассматриваемом интервале меняется слабо, либо существуют участки медленных и быстрых его изменений. Метод Рунге-Кутты с переменным шагом разбивает интервал не на равномерные шаги, а более оптимальным способом. Там, где решение меняется слабо, шаги выбираются более редкими, а в областях его сильных изменений — частыми. В результате, для достижения одинаковой точности требуется меньшее число шагов, чем для rkf ixed. Метод Булирша-Штера Buistoer часто оказывается более эффективным для поиска гладких решений.
График решения системы ОДУ (11.2—1) (листинг 11.4)
График решения системы ОДУ (11.2—1) (листинг 11.4)
График решения (слева) и фазовый портрет (справа) уравнения Ван дер Поля (листинг 11.8)
График решения (слева) и фазовый портрет (справа) уравнения Ван дер Поля (листинг 11.8)Решением уравнения Ван дер Поля являются колебания, вид которых для ц=1 показан на рис. 11.10. Они называются автоколебаниями и принципиально отличаются от рассмотренных нами ранее (например, колебаний маятника в разд. 11.3.2) тем, что их характеристики (амплитуда, частота, спектр) не зависят от начальных условий, а определяются исключительно свойствами самой динамической системы. Через некоторое время расчетов после выхода из начальной точки решение выходит на один и тот же цикл колебаний, называемый предельным циклом. Аттрактор типа предельного цикла является замкнутой кривой на фазовой плоскости. К нему асимптотически притягиваются все окрестные траектории, выходящие из различных начальных точек, как изнутри (рис. 11.10), так и снаружи (рис. 11.11) предельного цикла.

Жесткая сисема ОДУ химической кинетики
Листинг 11.12. Жесткая сисема ОДУ химической кинетики
Бросается в глаза сильно различающийся порядок коэффициентов при разных слагаемых. Именно степень этого различия чаще всего и определяет жесткость системы ОДУ. В качестве соответствующей характеристики выбирают матрицу Якоби (якобиан) векторной функции Fit,у), т.е. функциональную матрицу, составленную из производных F(t,y) (см. разд. "Частные производные" гл. 7). Чем вырожденнее матрица Якоби, тем жестче система уравнений. В приведенном примере определитель якобиана и вовсе равен нулю при любых значениях у„, yi и у2 (листинг 11.13, вторая строка). В первой строке листинга 11.13 приведено напоминание способа вычисления якобиана средствами Mathcad на примере определения элементов его первой строки.
Якобиан рассматриваемой системы ОДУ химический киметики
Листинг 11.13. Якобиан рассматриваемой системы ОДУ химический киметики
Для примера, приведенного в листинге 11.12, стандартным методом Вунге-Кутгы все-таки удается найти решение (оно показано на рис. 11.18). Однако для этого требуется очень большое число шагов, м=2000о, что делает (расчеты очень медленными. При меньшем числе шагов численному алгоритму не удается найти решение. В процессе работы алгоритма оно расходятся, и Mathcad вместо результата выдает ошибку о превышении предельно большого числа.
Еще один факт, на который стоит обратить внимание, — это различие в порядке величины получающегося решения. Как видно из рис. 11.18, концентрация первого реагента y1 существенно (в тысячи раз) превышает концентрацию остальных. Это свойство также очень характерно для жестких систем.
В принципе, можно было бы снизить жесткость системы "вручную", применяя масштабирование. Для этого нужно искусственно уменьшить искомую функцию yl, к примеру, в тысячу раз, разделив все слагаемые в системе ОДУ, содержащие yi, на 1000. После масштабирования для решения полученной системы методом Рунге-Кутты будет достаточно взять всего М=20 шагов.

Решение жесткой системы ОДУ химической кинетики
Листинг 11.14. Решение жесткой системы ОДУ химической кинетики
Расчеты показывают, что для получения того же результата (см. рис. 11.18) оказалось достаточно в тысячу раз меньшего количества шагов численного алгоритма, чем для стандартного метода Рунге-Кутты! Примерно во столько же раз требуется меньше компьютерного времени на проведение расчетов. Стоит ли говорить, что, если Вы имеете дело с жесткими (в той или иной степени) системами, применение описанных специальных алгоритмов просто необходимо.
Важно заметить, что до сих пор мы имели дело с примером не очень жесткой системы. Попробуйте вместо скоростей упомянутых химических реакций (см. разд. 11.5.1), 0.1, 103 и 102 взять другие числа, например 0.05, 10 и 107, соответственно. Заметим, что такое соотношение скоростей часто встречается в прикладных задачах химической кинетики и определяет куда более жесткую систему ОДУ. Ее уже никак не удается решить стандартными методами, поскольку число шагов численного метода должно быть просто гигантским. А между тем, алгоритмы для жестких ОДУ справляются с этой задачей с легкостью (рис. 11.19), причем практически при тех же значениях шага, что были взяты в листинге 11.14. Обратите внимание, что порядки величины решений для концентраций различных веществ на рис. 11.19 различаются еще сильнее, чем в предыдущем (менее жестком) примере.
Это еще раз доказывает, что одна и та же система ОДУ с различными коэффициентами может быть жесткой в разной степени В частности, приведенный выше пример генератора Ван дер Поля с параметром ц=5000 — это уже пример жесткой задачи.
В заключение приведем соответствующие встроенные функции, которые применяются для решения жестких систем ОДУ не на всем интервале, а только в одной заданной точке t1.

Решение задачи Коши для ОДУ первого порядка
Листинг 11.1. Решение задачи Коши для ОДУ первого порядка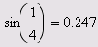
Не забывайте о том, что вставлять логические операторы следует при помощи панели инструментов Boolean (Булевы операторы). При вводе с клавиатуры помните, что логическому знаку равенства соответствует сочетание клавиш
+<=>
. Символ производной можно ввести как средствами панели Calculus (Вычисления), как это сделано в листинге 11.1, так и в виде штриха, набрав его с помощью сочетания клавиш
+
(соответствующий пример будет приведен ниже в листинге 11.3.) Выбирайте тот или иной способ представления производной из соображений наглядности представления результатов — на ход расчетов он не влияет.
Mathcad требует, чтобы конечная точка интегрирования ОДУ лежала правее начальной: t0
Решение задачи Коши для ОДУ первого порядка вторым способом
Листинг 11.2. Решение задачи Коши для ОДУ первого порядка вторым способом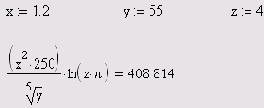
В листинге 11.2. приведен пример не лучшего стиля Mathcad-программиро-вания Сначала переменной у присвоено значение скаляра у=0 1, а затем этой же переменной присвоено матричное значение (результат решения ОДУ) Старайтесь избегать такого стиля, который ухудшает читаемость программы и может приводить, в более сложных случаях, к трудно опознаваемым ошибкам Неплохим решением было бы назвать результат по-другому, например u.
График решения рассматриваемого уравнения показан на рис. 11.1. Обратите внимание, что он соответствует получению решения в матричном виде (листинг 11.2), поэтому по осям отложены соответствующие столбцы, выделенные из матрицы у оператором <>
.
Пример, решенный в листингах 11.1—11.2, взят из области математической экологии и описывает динамику популяций с внутривидовой конкуренцией Сначала происходит рост численности популяции, близкий к экспоненциальному, а затем выход на стационарное состояние
Решение задачи Коши для ОДУ второго порядка
Листинг 11.3. Решение задачи Коши для ОДУ второго порядка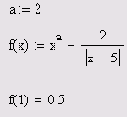

Решение системы двух ОДУ
Листинг 11.4. Решение системы двух ОДУ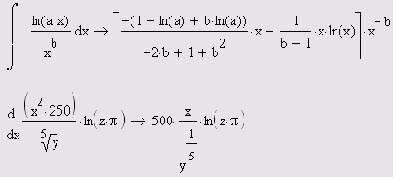
Самая важная — это первая строка листинга, в которой, собственно, определяется система ОДУ. Сравните рассматриваемую систему (разд. 11.2.1), записанную в стандартной форме, с формальной ее записью в Mathcad, чтобы не делать впоследствии ошибок. Во-первых, функция D, входящая в число параметров встроенных функций для решения ОДУ, должна быть функцией обязательно двух аргументов. Во-вторых, второй ее аргумент должен быть вектором того же размера, что и сама функция D. В-третьих, точно такой же размер должен быть и у вектора начальных значений уо (он определен во второй строке листинга).
Не забывайте, что векторную функцию D(t,y) следует определять через компоненты вектора у с помощью кнопки нижнего индекса (Subscript) с наборной панели Calculator (Калькулятор) или нажатием клавиши <[>
. В третьей строке листинга определено число шагов, на которых рассчитывается решение, а его последняя строка присваивает матричной переменной и результат действия функции rkfixed. Решение системы ОДУ будет осуществлено на промежутке (о, 50).
Как выглядит все решение, показано на рис. 11.3. Размер полученной матрицы будет равен (M+DX(N+I), т.е. Ю1хз. Просмотреть все компоненты матрицы и, которые не помещаются на экране, можно с помощью вертикальной полосы прокрутки. Как нетрудно сообразить, на этом рисунке отмечено выделением расчетное значение первого искомого вектора у0 на 12-м шаге u12.1=0.01. Это соответствует, с математической точки зрения, найденному значению У0(6.о)=0.07. Для вывода элементов решения в последней точке интервала используйте выражения типа Uм1=7.523x103.
Решение системы двух ОДУ
Листинг 11.5. Решение системы двух ОДУ
Чтобы попробовать альтернативный численный метод, достаточно в листинге 11.5 заменить имя функции buistoer на rkadapt.
Функции buistoer и rkadapt (те, что пишутся с маленькой буквы) не предназначены для нахождения решения в промежуточных точках интервала, хотя они и выдают их в матрице-результате. На рис. 11.6 показаны фазовые портреты рассматриваемой системы ОДУ, полученные с помощью buistoer (результат листинга 11.5) и с помощью rkadapt (при соответствующей замене третьей строки листинга 11.5). Видно, что несмотря на высокую точность (10-5) и верный результат на конце интервала, левый график мало напоминает правильный фазовый портрет (см. рис. 11.5 или правый график на рис. 11.6), начиная быть приемлемым только при предельно допустимом для обсуждаемых функций значении асс=10-16.
В заключение остановимся на влиянии выбора параметра асе на расчеты. Для этого воспользуемся простой программой, представленной на листинre 11.6. В ней из матрицы решения все той же задачи Коши взято лишь полученное значение одной из функций на правой границе интервала. Но зато этот результат оформлен в виде функции пользователя у(е), в качестве аргумента которой выбран параметр асе функции bulstoer.
Использование решения ОДУ для определения функции пользователя
Листинг 11.6. Использование решения ОДУ для определения функции пользователя
Вычисленный вид у(е) показан на рис. 11.7 вместе с аналогичным результатом для функции rkadapt. Как видно, в данном примере численные методы работают несколько по-разному. Метод Рунге-Кутты дает результат тем ближе к истинному, чем меньше выбирается е=асс. Метод Булирша-Штера демонстрирует менее естественную зависимость у (Б): даже при относительно больших е реальная точность остается хорошей (намного лучше метода Рунге-Кутты). Поэтому для экономии времени расчетов (подчеркнем еще раз: для данной конкретной задачи) в функции bulstoer можно выбирать и большие асе.
Чтобы обеспечить заданную точность, алгоритмы, реализованные во встроенных функциях, могут изменять как количество шагов, разбивающих интервал (t0.t1), так и их расположение вдоль интервала. Чтобы выяснить, на сколько шагов разбивался интервал при расчетах у(е)на рис. 11.7 для каждого Е, следует вычислить размер получающейся матрицы. Для этого можно, например, определить функции.
Модель "хищник-жертва"
Листинг 11.7. Модель "хищник-жертва"
Модель замечательна тем, что в такой системе наблюдаются циклическое увеличение и уменьшение численности и хищника (рис. 11.9), и жертвы, так часто наблюдаемое в природе. Фазовый портрет системы представляет собой концентрические замкнутые кривые, окружающие одну стационарную точку, называемую центром. Как видно, модельные колебания численности обеих популяций существенно зависят от начальных условий — после каждого периода колебаний система возвращается в ту же точку. Динамические системы с таким поведением называют негрубыми.

Модель Ван дер Поля (м=1)
Листинг 11.8. Модель Ван дер Поля (м=1)

Модель Лоренца
Листинг 11.9. Модель Лоренца

Матрица решений системы уравнений (листинг 11.4)
Матрица решений системы уравнений (листинг 11.4)
Обратите внимание на некоторое разночтение в обозначении индексов вектора начальных условий и матрицы решения В ее первом столбце собраны значения нулевой компоненты искомого вектора, во втором столбце — первой компоненты и т. д.
Чтобы построить график решения, надо отложить соответствующие компоненты матрицы решения по координатным осям" значения аргумента и<0> — вдоль оси х, а u<1> и u<2> — вдоль оси У (рис. 11.4). Как известно, решения обыкновенных дифференциальных уравнений часто удобнее изображать не в таком виде, а в фазовом пространстве, по каждой из осей которого откладываются значения каждой из найденных функций. При этом аргумент входит в них лишь параметрически. В рассматриваемом случае двух ОДУ такой график — фазовый портрет системы — является кривой на фазовой плоскости и поэтому особенно нагляден. Он изображен на рис. 11.5 (слева), и можно заметить, что для его построения потребовалось лишь поменять метки осей на u<1> и u<2>, соответственно.
Фазовый портрет типа, изображенного на рис 11.5, имеет одну стационарную точку (аттрактор), на которую "накручивается" решение В теории динамических систем аттрактор такого типа называется фокусом.
Модель "хищник—жертва"
Модель "хищник—жертва"Модель взаимодействия "хищник—жертва" независимо предложили в 1925— 1927 гг. Лотка и Вольтерра. Два дифференциальных уравнения (листинг 11.7) моделируют временную динамику численности двух биологических популяций жертвы Y0 и хищника Y1. Предполагается, что жертвы размножаются с постоянной скоростью с, а их численность убывает вследствие поедания хищниками. Хищники же размножаются со скоростью, пропорциональной количеству пищи (с коэффициентом r), и умирают естественным образом (смертность определяется константой D). В листинге рассчитываются три решения D, G, р для разных начальных условий.
Неверное решение более жесткого ОДУ методом Рунге-Кутты
Неверное решение более жесткого ОДУ методом Рунге-КуттыТаким образом, во-первых, мы выяснили, что одни и те же уравнения с разными параметрами могут быть как жесткими, так и нежесткими. Во-вторых, чем жестче уравнение, тем больше шагов в обычных численных методах требуется для его устойчивого решения. С классическим примером ОДУ из листинга 11.11 все получилось хорошо, т. к. оно было не очень жестким, и небольшое увеличение числа шагов разрешило все проблемы. Для решения обычными методами более жестких уравнений требуются миллионы, миллиарды и даже большее число шагов.
Некоторые ученые замечают, что в последние годы методы Рунге-Кутты стали уступать свое главенствующее положение среди алгоритмов решения ОДУ методам, способным решать жесткие задачи.
Исторически, интерес к жестким системам возник в середине XX века при изучении уравнений химической кинетики с одновременным присутствием очень медленно и очень быстро протекающих химических реакций. Тогда неожиданно оказалось, что считавшиеся исключительно надежными методы Рунгй-Кутты стали давать сбой при расчете этих задач. Рассмотрим классическую модель взаимодействия трех веществ (Робертсон, 1966), которая как нельзя лучше передает смысл понятия жесткости ОДУ.
Пусть вещество "0"- медленно превращается в "1": "0" -> "1" (со скоростью 0.1), вещество "1" при каталитическом воздействии самого себя превращается очень быстро в вещество "2" : "1" + "1" -> "2" + "1" (10^3). И, наконец, подобным! образом (но со средней скоростью) реагируют вещества "2" и "1" : "1" + "2" -> "0" + "2" (10^2). Система ОДУ, описывающая динамику концентрации реагентов, с попыткой решения методом Рунге-Кутты, приведена в листинге 11.12.
Решение нежестких ОДУ методом Рунге-Кутты (листинг 11.11)
Решение нежестких ОДУ методом Рунге-Кутты (листинг 11.11)На рис. 11.17 показано решение того же ОДУ с коэффициентом -50. Вас, несомненно, должен насторожить результат, выданный Mathcad. Характерная "разболтка" решения говорит о неустойчивости алгоритма. Первое, что можно сделать, — увеличить количество шагов в методе Рунге-Кутты. Для этого достаточно добавить третий параметр step в функцию odesoive(t,i,step). После нескольких экспериментов можно подобрать такое значение step, которое будет обеспечивать устойчивость решения. Читатель может самостоятельно убедиться, что при step>20 "разболтка" пропадает, и решение становится похожим на графики, показанные на рис. 11.16.

Решение системы Лоренца с измененным...
Решение системы Лоренца с измененным параметром г=10Замечательно, что решение подобных нелинейных динамических систем можно получить только численно, поэтому их изучение стало бурно развиваться с ростом возможностей вычислительной техники в последние полвека.
Решение уравнения осциллятора (листинг 11.3)
Решение уравнения осциллятора (листинг 11.3)В листинге 11.3 решено уравнение затухающего гармонического осциллятора, которое описывает, например, колебания маятника. Для модели маятника y(t) описывает изменения угла его отклонения от вертикали, y'(t) — угловую скорость маятника, y"(t) — ускорение, а начальные условия, соответственно, начальное отклонение маятника у (0) =0.1 и начальную скорость у' (0)= 0.
Второй способ решения ОДУ высшего порядка связан со сведением его к эквивалентной системе ОДУ первого порядка. Покажем на том же примере из листинга 11.3, как это делается. Действительно, если формально обозначить y0(t)sy(t), a yi(t)sy'(t)=y0'(t), то исходное уравнение запишется через функции y0(t) и y1(t) в виде системы двух ОДУ:
Именно эта система решается в качестве примера в разд. 11.3. Таким образом, любое ОДУ N-ГО порядка, линейное относительно высшей производной, можно свести к эквивалентной системе N дифференциальных уравнений.
Решение уравнения Ван дер Поля
Решение уравнения Ван дер Поля при других начальных условиях у=-2, у =-3Если компьютер у Вас не самый мощный, то расчет фазового портрета с рис. 11.10—11.11 в Mathcad может занять относительно продолжительное время, что связано с численным определением сначала решения y(t), а потом его производной. Время расчетов можно было бы существенно сократить, если использовать вместо вычислительного блока Given/Odesolve одну из встроенных функций, которые выдают решение в виде матрицы, например rkfixed.
Решение уравнения y' =y-y2 (листинг 11.2)
Решение уравнения y' =y-y2 (листинг 11.2)
Зависимость числа шагов от параметра асе численных методов
Зависимость числа шагов от параметра асе численных методов
Сравнив два результата применения rkadapt для k=30 и k=100, обратите внимание (рис. 11.8), как еще один параметр — максимальное число шагов k, влияет на вид м(е). Заметим, что такие же изменения параметра k на расчет м(е) посредством функции bulstoer влияют слабо.
Таким образом, проводя тестовые расчеты для различных задач и подбирая наилучший набор параметров, можно существенно сэкономить ресурсы компьютера. Конечно, проводить подобный анализ стоит в случаях, когда время расчетов играет важную роль.
Зависимость расчетного значения...
Зависимость расчетного значения одного из уравнений системы ОДУ на конце интервала от параметра асе (листинг 11.6)
Математический редактор MathCAD
О постановке краевых задач
12.1.1. О постановке краевых задачЧтобы лучше понять, что из себя представляют краевые задачи, рассмотрим их постановочную часть на конкретном физическом примере модели взаимодействия встречных световых пучков. Предположим, что надо определить распределение интенсивности оптического излучения в пространстве между источником (лазером) и зеркалом, заполненном некоторой средой (рис. 12.1). Будем считать, что от зеркала отражается R-Я часть падающего излучения (т. е. его коэффициент отражения равен к), а среда как поглощает излучение с коэффициентом ослабления а(х), так и рассеивает его. Причем коэффициент рассеяния назад равен г(х). В этом случае закон изменения интенсивности у0(х) излучения, распространяющегося вправо, и интенсивности у:(х) излучения влево определяется системой двух ОДУ первого порядка.
Для правильной постановки задачи требуется, помимо уравнений, задать такое же количество граничных условий. Одно из них будет выражать известную интенсивность излучения I0, падающего с левой границы х=0, а второе — закон отражения на его правой границе х=1:
Алгоритм стрельбы
12.1.2. Алгоритм стрельбыДля решения краевых задач в Mathcad реализован наиболее популярный алгоритм, называемый методом стрельбы или пристрелки (shooting method). Он, по сути, сводит решение краевой задачи к решению серии задач Коши с различными начальными условиями. Рассмотрим здесь его основной принцип на примере модели (рис. 12.1), а встроенные функции, реализующие этот алгоритм, приведем в следующем разделе.
Суть метода стрельбы заключается в пробном задании недостающих граничных условий на левой границе интервала и решении затем полученной задачи Коши хорошо известными методами (см. гл. 11). В нашем примере не хватает начального условия для Y1(0), поэтому сначала зададим ему произвольное значение, например Y1(0)=10. Конечно, такой выбор не совсем случаен, поскольку из физических соображений ясно, что, во-первых, интенсивность излучения — величина заведомо положительная, и, во-вторых, отраженное излучение должно быть намного меньше падающего. Решение задачи Коши с помощью функции rkfixed приведено в листинге 12.1.
Решение двухточечных краевых задач
12.1.3. Решение двухточечных краевых задачРешение краевых задач для систем ОДУ методом стрельбы в Mathcad достигается применением двух встроенных функций. Первая предназначена для двухточечных задач с краевыми условиями, заданными на концах интервала.
Как видно, функция sbval предназначена не для поиска собственно решения, т. е. неизвестных функций yi(x), а для определения недостающих начальных условий в первой точке интервала, т. е. yi(x). Чтобы вычислить yi(x) на всем интервале, требуется дополнительно решить задачу Коши.
Разберем особенности использования функции sbval на конкретном примере (листинг 12.2), описанном выше (см. разд. 12.1.1). Краевая задача состоит из системы двух уравнений (N=2), одного левого (L=1) и одного правого (N-L=2-1=1) граничного условия.
Решение краевых задач с дополнительным условием в промежуточной точке
12.1.4. Решение краевых задач с дополнительным условием в промежуточной точкеИногда дифференциальные уравнения определяются с граничными условиями не только на концах интервала, но и с дополнительным условием в некоторой промежуточной точке расчетного интервала. Чаше всего такие задачи содержат данные о негладких в некоторой внутренней точке интервала решениях. Для них имеется встроенная функция bvaif.it, также реализующая алгоритм стрельбы.
Рассмотрим действие функции bvaifit на знакомом примере модели взаимодействия пучков света (см. рис. 12.1), предположив, что в промежутке между xf=0.5 и x1=1.0 находится другая, оптически более плотная среда с другим коэффициентом ослабления излучения а(х)=3. Соответствующая краевая задача решена в листинге 12.3, причем разрывный показатель ослабления определяется в его второй строке.
Краевые задачи для ОДУ
12.1. Краевые задачи для ОДУПостановка краевых задач для ОДУ отличается от задач Коши, рассмотренных в главе 11, тем, что граничные условия для них ставятся не в одной начальной точке, а на обеих границах расчетного интервала. Если имеется система N обыкновенных дифференциальных уравнений первого порядка, то часть из N условий может быть поставлена на одной границе интервала, а оставшиеся условия — на противоположной границе.
Дифференциальные уравнения высших порядков можно свести к эквивалентной системе ОДУ первого порядка Сем. гл. 11).
Задачи на собственные значения для ОДУ
12.2. Задачи на собственные значения для ОДУЗадачи на собственные значения — это краевые задачи для системы ОДУ, в которой правые части зависят от одного или нескольких параметров К. Значения этих параметров неизвестны, а решение краевой задачи существует только при определенных Xk, которые называются собственными значениями (eigenvalues) задачи. Решения, соответствующие этим Xk, называют собственными функциями (eigenfunctions) задачи. Правильная постановка таких задач требует формулировки количества граничных условий, равного сумме числа уравнений и числа собственных значений. Физическими примерами задач на собственные значения являются, например, уравнение колебаний струны, уравнение Шредингера в квантовой механике, уравнения волн в резонаторах и многие другие.
С вычислительной точки зрения, задачи на собственные значения очень похожи на рассмотренные выше краевые задачи. В частности, для многих из них также применим метод стрельбы (см. разд. 12.1.2). Отличие заключается в пристрелке не только по недостающим левым граничным условиям, но еще и по искомым собственным значениям. В Mathcad для решения задач на собственные значения используются те же функции sbval и bvaifit. В их первый аргумент, т. е. вектор, присваивающий начальные значения недостающим начальным условиям, следует включить и начальное приближение для собственного значения.
Рассмотрим методику решения на конкретном примере определения собственных упругих колебаний струны. Профиль колебаний струны у(х) описывается линейным дифференциальным уравнением второго порядка.
где р(х) и q(x) — жесткость и плотность, которые, вообще говоря, могут меняться вдоль струны. Если струна закреплена на обоих концах, то граничные условия задаются в виде у(0)=у(1)=0. Сформулированная задача является частным случаем задачи Штурма-Лиувилля. Поскольку решается система двух ОДУ, содержащая одно собственное значение А,, то по идее задача требует задания трех (2+1) условий. Однако, как легко убедиться, уравнение колебаний струны — линейное и однородное, поэтому в любом случае решение у(х) будет определено с точностью до множителя. Это означает, что производную решения можно задать произвольно, например у' (0) =1, что и будет третьим условием. Тогда краевую задачу можно решать как задачу Коши, а пристрелку вести только по одному параметру — собственному значению.
Процедура поиска первого собственного значения представлена в листинге 12.5.
О разностном методе решения ОДУ
12.3.1. О разностном методе решения ОДУРазберем идею разностного метода решения краевых задач на примере взаимодействия световых пучков (см. рис. 12.1), переобозначив в системе (12.1,1) интенсивность излучения вправо на Y, а интенсивность излучения влево на у (просто в целях удобства, чтобы не писать индекс). Суть метода заключается в покрытии расчетного интервала сеткой из N точек. Тем самым определяются (N-I) шагов (рис. 12.7). Затем надо заменить дифференциальные уравнения исходной краевой задачи аппроксимирующими их уравнениями в конечных разностях, выписав соответствующие разностные уравнения для каждого 1-го шага. В нашем случае достаточно просто заменить первые производные из (12.1,1) их разностными аналогами (такой метод называется еще методом Эйлера).
Жесткие краевые задачи
12.3.2. Жесткие краевые задачиОдин из случаев, когда применение разностных схем может быть очень полезным, связан с решением жестких краевых задач (подробнее о жестких ОДУ читайте в гл. 11). В частности, рассматриваемая задача о встречных световых пучках становится жесткой при увеличении коэффициента ослабления а(х) в несколько десятков раз. Например, при попытке решить ее с а (х) :=100 с помощью листинга 12.2 вместо ответа выдается сообщение об ошибке "Can't converge to a solution. Encountered too many integration steps" (He сходится к решению. Слишком много шагов интегрирования). Это и неудивительно, поскольку жесткие системы характерны тем, что требуют исключительно малого значения шага в стандартных алгоритмах.
Для жестких задач неприменимы и явные разностные схемы, о которых рассказывалось в предыдущем разделе (см. разд. 12.3.1). Результат расчетов по программе листинга 12.6, например с а(х):=20 (рис. 12.9), дает характерную для неустойчивых разностных схем "разболтку" — колебания нарастающей амплитуды, не имеющие ничего общего с реальным решением.
Разностные схемы для ОДУ
12.3. Разностные схемы для ОДУМногие краевые задачи не поддаются решению методом стрельбы. Однако в Mathcad 11 других встроенных алгоритмов нет. Тем не менее, это не означает, что по-другому решать краевые задачи невозможно, ведь другие численные алгоритмы несложно запрограммировать самому пользователю. Рассмотрим возможную реализацию наглядного метода, называемого разностным, которым можно решать краевые задачи как для ОДУ, так и для дифференциальных уравнений в частных производных.
Иллюстрация метода стрельбы (листинг 12.1)
Иллюстрация метода стрельбы (листинг 12.1)
Конечно, описанный алгоритм несложно запрограммировать самому, оформив его как решение системы заданных алгоритмически уравнений, выражающих граничные условия на второй границе, относительно неизвестных пристрелочных начальных условий. Но делать этого нет необходимости, поскольку он оформлен в Mathcad в виде встроенных функций.
Решение пробной задачи Коши для модели (12.1, 1)
Листинг 12.1. Решение пробной задачи Коши для модели (12.1, 1)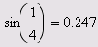
График полученных решений показан на рис. 12.2 (слева). Из него видно, что взятое наугад второе начальное условие не обеспечило выполнение граничного условия при х=1. И понятно, что для лучшего выполнения этого граничного условия следует взять большее значение yi(0). Возьмем, например, у1(0)=15, и вновь решим задачу Коши. Результат показан на том же рис. 12.2 (в центре). Граничное условие выполняется с лучшей точностью, но опять-таки оказалось недостаточным. Для еще одного значения у1(0)=20 получается решение, показанное на рис. 12.2 (справа). Из сравнения двух правых графиков легко заключить, что недостающее начальное условие больше 15, но меньше 20. Продолжая подобным образом "пристрелку" по недостающему начальному условию, возможно отыскать правильное решение краевой задачи.
В этом и состоит принцип алгоритма стрельбы. Выбирая пробные начальные условия (проводя пристрелку) и решая соответствующую серию задач Коши, можно найти то решение системы ОДУ, которое (с заданной точностью) удовлетворит граничному условию (или, в общем случае, условиям) на другой границе расчетного интервала.
Решение краевой задачи
Листинг 12.2. Решение краевой задачи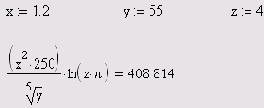
Первые три строки листинга задают необходимые параметры задачи и саму систему ОДУ. В четвертой строке определяется вектор г. Поскольку правое граничное условие всего одно, то недостающее начальное условие тоже одно, соответственно, и вектор z имеет только один элемент z0. Ему необходимо присвоить начальное значение (мы приняли z0=io, как в листинге 12.1), чтобы запустить алгоритм стрельбы (см. разд 12.1.2).
Начальное значение фактически является параметром численного метода и поэтому может сильно повлиять на решение краевой задачи.
В следующей строке листинга векторной функции ioad(x,z) присваиваются левые граничные условия. Эта функция аналогична векторной переменной, определяющей начальные условия для встроенных функций, решающих задачи Коши. Отличие заключается в записи недостающих условий. Вместо конкретных чисел на соответствующих местах пишутся имена искомых элементов вектора z. В нашем случае вместо второго начального условия стоит аргумент z0 функции load. Первый аргумент функции load — это точка, в которой ставится левое граничное условие. Ее конкретное значение определяется непосредственно в списке аргументов функции sbval.
Следующая строка листинга определяет правое граничное условие, для введения которого используется функция score(х,у). Оно записывается точно так же, как система уравнений в функции D. Аргумент х функции score аналогичен функции load и нужен для тех случаев, когда граничное условие явно зависит от координаты х. Вектор score должен состоять из такого же числа элементов, что и вектор z.
Реализованный в функции sbval алгоритм стрельбы ищет недостающие начальные условия таким образом, чтобы решение полученной задачи Коши делало функцию score (х, у) как можно ближе к нулю. Как видно из листинга, результат применения sbval для интервала (0,1) присваивается векторной переменной и. Этот вектор похож на вектор z, только в нем содержатся искомые начальные условия вместо приближенных начальных значений, заданных в z. Вектор и содержит, как и z, всего один элемент I10. С его помощью можно определить решение краевой задачи у(х) (последняя строка листинга). Тем самым, функция sbval сводит решение краевых задач к задачам Коши. График решения краевой задачи показан на рис. 12.3.
Краевая задача с фанячным условием в промежуточной точке
Листинг 12.3. Краевая задача с фанячным условием в промежуточной точке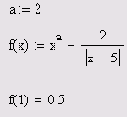
Система уравнений и левое краевое условие вводится так же, как и в предыдущем листинге для функции sbvai. Обратите внимание, что таким же образом записано и правое краевое условие. Для того чтобы ввести условие отражения на правой границе, пришлось определить еще один неизвестный пристрелочный параметр z20. Строка листинга, в которой определена функция score, задает условие стрельбы — сшивку двух решений в точке xf. В самой последней строке листинга выдан ответ — определенные численным методом значения обоих пристрелочных параметров, которые объединены в вектор и (мы применили в предпоследней строке операцию транспонирования, чтобы результат получился в форме вектора, а не матрицы-строки).
Для корректного построения графика решения лучше составить его из двух частей — решения задачи Коши на интервале (x0,xf) и другой задачи Ко-ши для интервала (xf,x1). Реализация этого способа приведена в листинге 12.4, который является продолжением листинга 12.3. В последней строке листинга 12.4 выведено значение второй искомой функции на правой границе интервала. Всегда полезно проконтролировать, что оно совпадает с соответствующим пристрелочным параметром (выведенном в последней строке листинга 12.3).
Решение краевой задачи (продолжение 12.3)
Листинг 12.4. Решение краевой задачи (продолжение 12.3)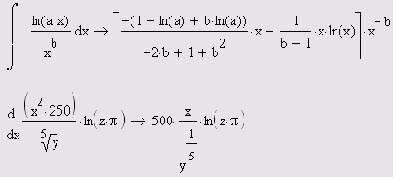
Решение краевой задачи приведено на рис. 12.5. С физической точки зрения естественно, что интенсивность света уменьшается быстрее по мере распространения в более плотной среде в правой половине расчетного интервала. В средней точке xf=0.5, как и ожидалось, производные обоих решений имеют разрыв.
Еще один пример решения краевых задач с разрывными коэффициентами ОДУ приведен в справочной системе Mathcad.
Решение задачи о собственных колебаниях струны
Листинг 12.5. Решение задачи о собственных колебаниях струны
В первых двух строках листинга определяются функции, входящие в задачу, в том числе р'(х):=о, и границы расчетного интервала (0,1). В третьей строке дается начальное приближение к собственному значению А0, в четвертой вводится система ОДУ. Обратите внимание, что она состоит не из двух, а из трех уравнений. Первые два из них определяют эквивалентную систему ОДУ первого порядка, а третье необходимо для задания собственного значения в виде еще одного компонента у2 искомого вектора у. Поскольку, по определению, собственное значение постоянно при всех х, то его производная должна быть приравнена нулю, что отражено в последнем уравнении. Важно также, что во втором из уравнений собственное значение записано как у2, поскольку является одним из неизвестных.
В следующих двух строках листинга задается левое граничное условие, включающее и недостающее условие на собственное значение для третьего уравнения, и правое граничное условие у0=о. В предпоследней строке листинга обычным образом применяется функция sbval, а в последней выводится результат ее работы вместе с известным аналитически собственным значением n2 pi2. Как легко убедиться, мы нашли первое собственное значение для n=1, а чтобы найти другие собственные значения, необходимо задать другие начальные приближения к ним (в третьей строке листинга 12.5). Например, выбор Lо=50 приводит ко второму собственному значению 22 pi2, Lо=50 — к третьему 32 pi2.
Чтобы построить график соответствующей собственной функции, надо добавить в листинг строку, программирующую решение задачи Коши, например, такую: u:=rkfixed(load(a,A), а, b, 100, D). Полученные кривые показаны на рис. 12.6 в виде коллажа трех графиков, рассчитанных для трех собственных значений.
Примеры решения нескольких задач на собственные значения можно найти в разделе Mathcad Resources.
Реализация явной разностной схемы
Листинг 12.6. Реализация явной разностной схемы
Дадим минимальные комментарии, надеясь, что заинтересовавшийся читатель с карандашом в руках разберется в порядке индексов и соответствии матричных элементов, а возможно, составит и более удачную программу.
В первой строке листинга определяются функции и константы, входящие в модель, во второй задается число точек сетки N=5 и ее равномерный шаг. Следующие две строки определяют матричные коэффициенты, аппроксимирующие уравнения для уi а пятая и шестая — для ух. Седьмая и восьмая строки листинга задают, соответственно, левое и правое граничное условие, а строки с девятой по одиннадцатую — правые части системы (3). В следующей строке завершается построение матрицы А вырезанием из нее левого нулевого столбца. В предпоследней строке листинга применена встроенная функция isolve для решения системы (3), а в последней выведены рассчитанные ею неизвестные граничные значения. Графики решения приведены на рис. 12.8, причем первые N элементов итогового вектора есть вычисленное излучение вперед, а последние N элементов — излучение назад.
Реализация неявной разностной схемы для жесткой краевой задачи
Листинг 12.7. Реализация неявной разностной схемы для жесткой краевой задачи
Не будем специально останавливаться на обсуждении листинга 12.7, поскольку он почти в точности повторяет предыдущий листинг. Отличие заключается лишь в формировании матрицы А другим способом, согласно неявной схеме. Решение, показанное на рис. 12.10, демонстрирует, что произошло "небольшое чудо": "разболтка" исчезла, а распределение интенсив-ностей стало физически предсказуемым. Обратите внимание, что (из-за взятого нами слишком большого коэффициента ослабления излучения) отраженный пучок света имеет очень маленькую интенсивность, и ее пришлось построить на графике с увеличением в тысячу раз.
Модель для постановки краевой задачи
Модель для постановки краевой задачи
Полученную задачу называют краевой (boundary value problem), поскольку условия поставлены не на одной, а на обеих границах интервала (0,1). И, в связи с этим, их не решить методами предыдущей главы, предназначенными для задач с начальными условиями. Далее для показа возможностей Mathcad будем использовать этот пример с R=I и конкретным видом a(x)=const=i и r(x)=const=0.1, описывающим случай изотропного (не зависящего от координаты х) рассеяния.
Модель рис. 12.1 привела к краевой задаче для системы линейных ОДУ. Она имеет аналитическое решение в виде комбинации экспонент. Более сложные, нелинейные задачи, возможно решить только численно. Нетрудно сообразить, что модель станет нелинейной, если сделать коэффициенты ослабления и рассеяния зависящими от интенсивности излучения. Физически это будет соответствовать изменению оптических свойств среды под действием мощного излучения.
Модель встречных световых пучков привела нас к системе уравнений (1), в которые входят производные только по одной переменной х. Если бы мы стали рассматривать более сложные эффекты рассеяния в стороны (а не только вперед и назад), то в уравнениях появились бы частные производные по другим пространственным переменным у и z. В этом случае получилась бы краевая задача для уравнений в частных производных, решение которой во много раз сложнее ОДУ.
Неверное решение жесткой краевой задачи по неустойчивой явной разностной схеме
Неверное решение жесткой краевой задачи по неустойчивой явной разностной схеме
Выходом из положения будет использование неявных разностных схем. Применительно к нашей задаче достаточно заменить правые части уравнений (1) значениями не на левой, а на правой границе каждого шага.
Граничные условия, конечно, можно оставить в том же виде (2). Поскольку мы имеем дело с линейными дифференциальными уравнениями, то и схему (4) легко будет записать в виде матричного равенства (3), перегруппировывая соответствующим образом выражение (4) и приводя подобные слагаемые. Разумеется, полученная матрица А будет иной, нежели матрица А для явной схемы (1). Поэтому и решение (реализация неявной схемы) может отличаться от изображенного на рис. 12.9 результата расчетов по явной схеме. Программа, составленная для решения системы (4), приведена в листинге 12.7.
Первые три собственные функции задачи колебаний струны (коллаж трех графиков)
Первые три собственные функции задачи колебаний струны (коллаж трех графиков)
показано решение той же
Решение краевой задачи для R=0
На рис. 12. 4 показано решение той же самой краевой задачи, но с другим правым граничным условием, соответствующим R=0, т. е. без зеркала на правой границе. В этом случае слабый обратный пучок света образуется исключительно за счет обратного рассеяния излучения от лазера. Конечно, многие из читателей уже обратили внимание, что реальная физическая среда не может создавать такого большого рассеяния назад. Иными словами, более реальны значения r(х)<<а(х). Однако, когда коэффициенты в системе ОДУ при разных ух очень сильно (на порядки) различаются, система ОДУ становится жесткой, и функция sbval не может найти решения, выдавая вместо него сообщение об ошибке("Соuld not find a solution").
Метод стрельбы не годится для решения жестких краевых задач. Поэтому алгоритмы решения жестких ОДУ в Mathcad приходится программировать самому (см. разд. 12.3).
Решение краевой задачи для R=1 (листинг 12.2)
Решение краевой задачи для R=1 (листинг 12.2)
Решение краевой задачи разностным методом (листинг 12.6)
Решение краевой задачи разностным методом (листинг 12.6)
Как мы увидели, реализация в Mathcad разностных схем вполне возможна и не слишком трудоемка — предложенная программа состоит всего из двух десятков математических выражений. Конечно, для их написания требуется и время, и часто кропотливые расчеты, но, собственно, в этом и состоит работа математика. Кстати говоря, при небольшом числе шагов, расчеты по разностным схемам не требуют существенного времени (программа, приведенная в листинге 12.6, работает быстрее, чем метод стрельбы, встроенный в функцию sbval). Существуют, кроме того, весьма очевидные для многих читателей пути ускорения расчетов, связанные с применением более подходящих методов решения систем линейных уравнений с разреженной матрицей.
Решение краевой задачи разностным методом (листинг 12.7)
Решение краевой задачи разностным методом (листинг 12.7)
Решение краевой задачи с разрывом в хf=0.5 (листинги 12.3—12.4)
Решение краевой задачи с разрывом в хf=0.5 (листинги 12.3—12.4)
Ради справедливости необходимо заметить, что разобранную краевую задачу легко решить и с помощью функции sbval, заменив в листинге 12.2 зависимость а(х) на третью строку листинга 12.3. В этом случае листинг 12.2 даст в точности тот же ответ, что показан на рис. 12.5. Однако в определенных случаях (в том числе из соображений быстроты расчетов) удобнее использовать функцию bvaif it, т. е. вести пристрелку с обеих границ интервала.
Если Вы имеете дело с подобными уравнениями, попробуйте сначала решить их как обычную краевую задачу с помощью более надежной и легкой в применении функции sbval.
Сетка, покрывающая расчетный интервал
Сетка, покрывающая расчетный интервал
Существует множество способов аппроксимации дифференциальных уравнений разностными. От выбора конкретного варианта зависит не только простота, быстрота и удобство вычислений, но и сама возможность получения правильного ответа.
Получилась система (по числу шагов) 2 (N-1) разностных линейных алгебраических уравнений с 2N неизвестными Yi и уi,.. Для того чтобы она имела единственное решение, надо дополнить число уравнений до 2N. Это можно сделать, записав в разностном виде оба граничных условия:
Y0=I0, YN=RYN (2)
Сформированная полная система алгебраических уравнений называется разностной схемой, аппроксимирующей исходную краевую задачу. Обратите внимание, что правые части разностных уравнений системы (1) на каждом шаге записаны для левой границы шага. Такие разностные схемы называют явными, т. к. все значения Yi+1 и Y1+i находятся в левой части уравнений. Полученную явную разностную схему легко записать в матричной форме
Az=B, (3)
где z — неизвестный вектор, получающийся объединением векторов Y и у. Решив систему (3), мы получим решение краевой задачи.
На самом деле, все несколько сложнее, поскольку, вообще говоря, необходимо еще доказать, что, во-первых, разностная схема действительно аппроксимирует дифференциальные уравнения и, во-вторых, при N разностное решение действительно сходится к дифференциальному.
Процесс решения системы разностных уравнений называют также реализацией разностной схемы. Программа, которая решает рассматриваемую краевую задачу разностным методом, приведена в листинге 12.6.
Математический редактор MathCAD
Пример: уравнение диффузии тепла
13.1.2. Пример: уравнение диффузии теплаНа протяжении всей главы мы будем использовать в качестве примера очень наглядное и имеющее различные, от очевидных до самых неожиданных, решения уравнение теплопроводности.
Постановка задач
13.1. Постановка задач13.1.1. Классификация уравнений в частных производных
Постановка задач для уравнений в частных производных включает определение самого уравнения (или системы нескольких уравнений), а также необходимого количества краевых условий (число и характер задания которых определяется спецификой уравнения). По своему названию уравнения должны содержать частные производные неизвестной функции и (или нескольких функций, если уравнений несколько) по различным аргументам, например пространственной переменной х и времени t. Соответственно, для решения задачи требуется вычислить функцию нескольких переменных, например u
Явная схема Эйлера
13.2.1. Явная схема ЭйлераРассмотрим сначала математические аспекты построения разностной схемы для уравнения диффузии тепла, а затем приведем примеры работы разработанного алгоритма применительно к линейному и нелинейному уравнениям.
Неявная схема Эйлера
13.2.2. Неявная схема ЭйлераВ отличие от явной схемы Эйлера, неявная является безусловно устойчивой (т. е. не выдающей "разболтки" ни при каких значениях коэффициента Куранта). Однако, ценой устойчивости является необходимость решения на каждом шаге по времени системы алгебраических уравнений.
О возможности решения многомерных уравнений
13.2.3. О возможности решения многомерных уравненийВсе, что было сказано до сих пор, касалось исключительно способов решения одномерных (в смысле пространственных координат) уравнений. И алгоритмы разностных схем, и встроенные функции, включая появившиеся в 11-й версии (см. следующий разд.), относились к уравнениям, зависящим от одной пространственной координаты.
Можно ли при помощи Mathcad решать двумерные или трехмерные (пространственные) уравнения? С точки зрения программирования пользователем численных алгоритмов типа метода сеток, принципиальных ограничений нет. Разумеется, если сначала аккуратно выписать разностную схему
соответствующего многомерного дифференциального уравнения, то вполне возможно запрограммировать ее при помощи описанных нами средств. Самым главным противодействием будет существенное увеличение времени расчетов. Простая оценка необходимого количества операций показывает, что ввод зависимости уравнения от второй пространственной координаты многократно увеличивает число разностных уравнений, которые должны решаться при реализации каждого шага по времени. К примеру, если используется пространственная сетка из 100 узлов по каждой координате, то вместо 102 разностных уравнений на каждом шаге придется решать уже 104 уравнений, т. е. объем вычислений сразу же возрастает в 100 раз. Вообще говоря, пакет Mathcad не является экономичной средой вычислений, и бороться с их сильно возрастающим объемом пользователю следует еще на этапе разработки алгоритма. Хорошим примером такой борьбы может служить применение специфических алгоритмов, типа метода прогонки (см. разд. "Алгоритм прогонки" этой главы).
Приведем некоторые дополнительные замечания, связанные с возможностью осуществить редукцию громоздких (в смысле организации вычислений) двумерных задач к более простым. Рассмотрим ради примера двумерное уравнение теплопроводности (1) без источника с нулевыми граничными условиями и некоторым начальным двумерным распределением температуры по расчетной поверхности:
Произведем дискретизацию данного уравнения по временной координате, заменяя первую производную ее разностным аналогом и несколько перегруппировывая слагаемые и множители:
Как Вы видите, мы используем неявную разностную схему, заранее заботясь о том, чтобы разностная задача была более устойчивой. Здесь ui(х,у) — известная с предыдущего шага по времени функция двух пространственных переменных, а ui+1(х,у) - функция, подлежащая определению при реализации каждого шага по времени.
Можно посмотреть на полученную задачу с несколько другой стороны — а именно как на дифференциальное уравнение относительно неизвестной функции двух переменных ui+1(x,y). Подчеркнем, что такое уравнение получается для каждого шага по времени, т. е. для реализации всей разностной схемы требуется решить большое число таких уравнений.
С предложенной точки зрения, на каждом временном шаге необходимо решить некоторое двумерное эллиптическое линейное уравнение, причем его граничные условия определяются граничными условиями исходной задачи.
Это уравнение очень похоже на уравнение Пуассона с той лишь разницей, что в его правую часть, описывающую источник, входит неизвестная функция (к счастью, линейно). Таким образом, зависимость от найденного на предыдущем шаге по времени решения определяется зависимостью от него источника, т. е. правой части.
Суммируя сказанное, можно констатировать, что если Вы имеете запрограммированный алгоритм решения выписанного эллиптического уравнения, чуть более сложного, чем уравнение Пуассона, то его с легкостью можно использовать в качестве подпрограммы реализации разностной схемы двумерного уравнения теплопроводности. Забегая вперед, приходится отметить, что, к сожалению, встроенные функции Mathcad для решения уравнения Пуассона в данном случае не годятся в качестве такой подпрограммы, поскольку предполагают независимость источника от самой неизвестной функции и могут справляться лишь с правой частью, зависящей только от пространственных координат (см разд 13.3.2).
Не будем далее останавливаться на способах решения многомерных уравнений, ограничившись этими замечаниями относительно путей оптимизации алгоритмов их решения.
Разностные схемы
13.2. Разностные схемыРассмотрим одномерное уравнение теплопроводности (3) и на его примере разберем наиболее часто использующийся для численного решения уравнений в частных производных метод сеток. Выпишем еще раз само уравнение а также и начальное и граничные условия которые необходимы для правильной с математической точки зрения постановки задачи.
Основная идея численного решения уравнений в частных производных очень похожа на метод решения краевых задач для ОДУ, рассмотренный нами в предыдущей главе. Основным отличием от ОДУ является необходимость дискретизации уравнения не по одной, а по нескольким переменным (в зависимости от размерности задачи).
Таким образом, сначала следует покрыть расчетную область (x,t) сеткой и использовать затем узлы этой сетки для разностной аппроксимации уравнения. В результате, вместо поиска непрерывных зависимостей u(x,t) достаточно будет отыскать значения функции в узлах сетки (а ее поведение в промежутках между узлами может быть получено при помощи построения какой-либо интерполяции). По этой причине дискретное представление функции и часто называют сеточной функцией.
Поскольку уравнения в частных производных по определению зависят от производных неизвестных функций по нескольким переменным, то способов дискретизации этих уравнений, может быть, как правило, несколько. Конфигурацию узлов, используемую для разностной записи уравнений в частных производных на сетке, называют шаблоном, а полученную систему разностных уравнений - разностной схемой. О принципах построения разностных схем, и, в частности, о классах явных и неявных схем, мы уже подробно говорили на примере краевых задач для ОДУ (см. разд. 12.3.1), поэтому, излишне не повторяясь, перейдем к рассмотрению типичных особенностей уравнений в частных производных, которые возникают при разработке и реализации разностных схем.
Параболические и гиперболические уравнения
13.3.1. Параболические и гиперболические уравненияВ новой версии Mathcad 11 разработчики впервые применили встроенную функцию pdesolve для решения уравнений в частных производных, отлично осознавая значимость этих задач для современного исследователя и инженера. Эта функция применяется в рамках вычислительного блока, начинающегося ключевым словом Given и пригодна для решения различных гиперболических и параболических уравнений.
Встроенная функция для решения одномерного уравнения (или системы уравнений) в частных производных (того, которое определит пользователь в рамках вычислительного блока Given), зависящего от времени t и пространственной координаты х, имеет целый набор различных аргументов и работает следующим образом.
В качестве примера использования этой новой функции Mathcad 11 (листинг 13.4) используем то же самое одномерное уравнение теплопроводности (5) с граничными и начальными условиями (6) и (7).
Эллиптические уравнения
13.3.2. Эллиптические уравненияРешение эллиптических уравнений в частных производных реализовано только для единственного типа задач - двумерного уравнения Пуассона. Это уравнение содержит вторые производные функции u(х,у) по двум пространственным переменным:
Уравнение Пуассона описывает, например, распределение электростатического поля u(х,у) в двумерной области с плотностью заряда f (х,у) или (см. разд. 13.1.2) стационарное распределение температуры u(х,у) на плоскости, в которой имеются источники (или поглотители) тепла с интенсивностью f (х,у).
Несмотря на то, что применение встроенных функций, описанных в данном разделе, анонсировано разработчиками Mathcad только для уравнения Пуассона, их можно применять и для решения других уравнений, даже необязательно эллиптического типа. О том, как осуществить такие расчеты, написано в конце данного раздела.
Встроенные функции для решения уравнений в частных производных
13.3. Встроенные функции для решения уравнений в частных производныхКак видно из предыдущего раздела, с уравнениями в частных производных вполне можно справиться, и не прибегая к специфическим средствам Mathcad. Между тем, в пакете Mathcad 11 имеется несколько встроенных функций, при помощи которых можно автоматизировать процесс решения дифференциальных уравнений в частных производных. Рассмотрим в данном разделе основные аспекты их применения, отмечая не только инструкции по их применению, описанные разработчиками Mathcad, но также и некоторые "скрытые" возможности этих функций.
Алгоритм прогонки
Алгоритм прогонкиПриведем в данном разделе описание чрезвычайно популярного алгоритма реализации неявных разностных схем, который называется методом прогонки. Этот алгоритм имел историческое значение для становления технологий расчетов уравнений в частных производных, и мы просто не можем не упомянуть о нем в этой книге.
Сразу оговоримся, что его применение для решения уравнений в частных производных в среде Mathcad может быть оправдано, только если Вы работаете с очень частыми сетками, которые приводят к системам разностных уравнений большой размерности и, соответственно, очень долгому времени вычислений.
Основным вычислительным ядром программы, реализующей на Mathcad неявную разностную схему, было решение (на каждом временном слое) системы линейных алгебраических уравнений, задаваемых матрицей А. Заметим, что эта матрица, как говорят, имеет диагональное преобладание, а точнее, является трехдиагоналъной (рис. 13.13). Все ее элементы, кроме элементов на главной диагонали и двух соседних диагоналях, равны нулю. С точки зрения оптимизации быстродействия алгоритма, применение встроенной функции isolve является весьма расточительным, поскольку основной объем арифметических операций, выполняемых компьютером (а он составляет, как нетрудно убедиться величину порядка M2), сводится к непроизводительному перемножению нулей.
Численное решение уравнения теплопроводности...
Численное решение уравнения теплопроводности при помощи явной схемы Эйлера (см. листинг 13.1 ниже с временным шагом т=0.0015)Характерная "разболтка" решения как раз и является проявлением неустойчивости явной схемы Эйлера для выбранного соотношения шагов по времени и пространству. В теории численных методов показывается, что явная схема Эйлера для уравнения теплопроводности устойчива при значениях коэффициента Куранта, меньших 1, и неустойчива в противоположном случае. Иными словами, существует ограничение для выбора соотношения шагов, заключающееся в том, что для расчета на более частых пространственных сетках необходимо использовать также и малые шаги по времени

Как несложно убедиться, для т=0.0005 коэффициент Куранта C=0.4, для т=0.0010 он все еще меньше единицы C=0.8, а для т=0.0015 решение уже больше единицы: C=1.2, в связи с чем схема становится неустойчивой (рис 13.10).
Двумерное динамическое уравнение
Двумерное динамическое уравнениеРассмотрим следующее параболическое уравнение в частных производных, зависящее от трех переменных — двух пространственных х и у, а также от времени t:
Выражение в скобках в правой части уравнения (сумму вторых пространственных производных функции u часто, ради краткости, обозначают при помощи оператора Лапласа: du).
Это уравнение называется двумерным уравнением теплопроводности или, по-другому, уравнением диффузии тепла. Оно описывает динамику распределения температуры u(x,y,t) на плоской поверхности (например, на металлической пластине) в зависимости от времени (рис. 13.1). Физический смысл коэффициента в, который, вообще говоря, может быть функцией как координат, так и самой температуры, заключается в задания скорости перетекания тепла от более нагретых областей в менее нагретые. Функция ф(х,у,t,u) описывает приток тепла извне, т.е. источники тепла, которые также могут зависеть как и от пространственных координат (что задает локализацию источников), так и от времени и температуры и.
Физическая модель одномерного уравнения теплопроводности
Физическая модель одномерного уравнения теплопроводности
Одномерное уравнение намного проще двумерного, поскольку объем вычислений для реализации алгоритма его численного решения не так велик. Типичное решение одномерного уравнения диффузии тепла с коэффициентом диффузии D=2, нулевым источником ф=0 и начальным распределением температуры в форме нагретой центральной области стержня показано (в виде графика поверхности) на рис. 13.4.
Начиная с новой версии Mathcad 11, для решения одномерных параболических и гиперболических уравнений можно применять новую встроенную функцию pdesolve.
Физическая модель, описываемая двумерным уравнением теплопроводности
Физическая модель, описываемая двумерным уравнением теплопроводности
Для того чтобы правильно поставить краевую задачу для двумерного уравнения теплопроводности, следует определить следующие дополнительные условия:
График линий уровня решения уравнения Пуассона (листинг 13.6)
График линий уровня решения уравнения Пуассона (листинг 13.6)
Параметр численного алгоритма характеризует скорость сходимости итераций. Он должен быть числом от о до 1. В матрице граничных условий v необходимо задать только граничные элементы, исходя из значения краевых условий по периметру расчетной области. Прочие (внутренние) элементы этой матрицы служат для задания начального приближения к решению. Суть алгоритма релаксации сводится к тому, что в ходе итераций происходит проверка уравнений и соответствующая коррекция значений искомой функции в каждой точке. Если начальное приближение выбрано удачно, то можно надеяться, что алгоритм сойдется ("срелаксирует") к правильному решению.
Все матрицы, задающие как коэффициенты разностной схемы a,b,c,d,e, граничные условия v, так и само решение F, должны иметь одинаковый размер (M+1)х(M+1), соответствующий размеру расчетной области. При этом целое число м обязательно должно быть степенью двойки: M=2".
Решение уравнения Пуассона с тремя источниками разной интенсивности при помощью функции relax приведено в листинге 13.7.
График поверхности решения уравнения Пуассона (листинг 13.6)
График поверхности решения уравнения Пуассона (листинг 13.6)
Линейное и нелинейное уравнения
Линейное и нелинейное уравненияЕсли присмотреться к уравнению диффузии тепла внимательнее, то можно условно разделить практические случаи его использования на два типа.
Линейное уравнение
Линейное уравнениеСделанные замечания относительно реализации явной схемы для уравнения диффузии тепла сразу определяют алгоритм ее программирования в Mathcad. Для решения задачи нужно аккуратно ввести в листинг соответствующие формулы при помощи элементов программирования.
Решение системы разностных уравнений (9) для модели без источников тепла, т. е. ф(х, T, t)=o и постоянного коэффициента диффузии D=const приведена в листинге 13.1. В его первых трех строках заданы шаги по временной и пространственной переменным т и Д, а также коэффициент диффузии D, равный единице. В следующих двух строках заданы начальные (нагретый центр области) и граничные (постоянная температура на краях) условия, соответственно. Затем приводится возможное программное решение разностной схемы, причем функция пользователя v(t) задает вектор распределения искомой температуры в каждый момент времени (иными словами, на каждом слое), задаваемый целым числом t.
Явная схема для линейного уравнения теплопроводности
Листинг 13.1. Явная схема для линейного уравнения теплопроводности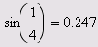
Неявная схема для линейного уравнения теплопроводности
Листинг 13.2. Неявная схема для линейного уравнения теплопроводности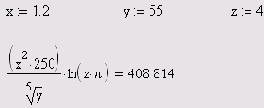
Алгорктм прогонки (продолжена листинга 13.2)
Листинг 13.3. Алгорктм прогонки (продолжена листинга 13.2)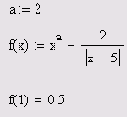
Решение одномерного уравнения теплопроводности
Листинг 13.4. Решение одномерного уравнения теплопроводности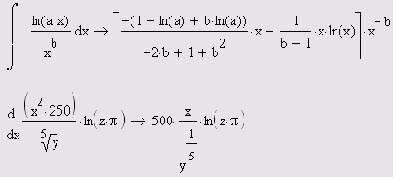
Для корректного использования функции Pdesolve предварительно, после ключевого слова Given, следует записать само уравнение и граничные условия при помощи логических операторов (для их ввода в Mathcad существует специальная панель). Обратите внимание, что уравнение должно содержать имя неизвестной функции u(x,t) вместе с именами аргументов (а не так, как она записывается в пределах встроенной функции Pdesolve). Для идентификации частных производных в пределах вычислительного блока следует использовать нижние индексы, например, uxx(,t) для обозначения второй производной функции и по пространственной координате х..
Как видно из рис. 13.14, на котором изображены результаты расчетов по листингу 13.4, встроенная функция с успехом справляется с уравнением диффузии, отыскивая уже хорошо знакомое нам решение. Заметим, что использование встроенной функции Pdesolve связано с довольно громоздкими вычислениями, которые могут отнимать существенное время.
Как Вы можете заметить, выбирать величину шага по пространственной и временной переменным может как сам алгоритм, так и пользователь (неявным образом, через число узлов сетки). Читателю предлагается повторить вычисления листинга 13.4 для различных комбинаций параметров (главным образом, числа узлов сетки), чтобы проверить, в каких случаях алгоритм встроенной функции справляется с задачей, выдавая верное решение, а в каких дает сбой.
Приведем еще один пример применения функции Pdesolve для решения уравнений в частных производных. Рассмотрим одномерное волновое уравнение, которое описывает, например, свободные колебания струны музыкального инструмента:
Решение волнового уравнения.
Листинг 13.5. Решение волнового уравнения.
Решение уравнения Пуассона с нулевыми граничными условиями.
Листинг 13.6. Решение уравнения Пуассона с нулевыми граничными условиями.
В первой строке листинга задается значение M=32, в двух следующих строках создается матрица правой части уравнения Пуассона, состоящая из всех нулевых элементов, за исключением одного, задающего расположение источника. В последней строке матрице G присваивается результат действия функции multigrid. Обратите внимание, первый ее аргумент сопровождается знаком "минус", что соответствует записи правой части уравнения Пуассона (11). Графики решения показаны на рис. 13.16 и 13.17 в виде трехмерной поверхности и линий уровня, соответственно.
содержит пример использования...
Листинг 13.6 содержит пример использования функции multigrid для расчета краевой задачи на области ззхзз точки и точечным источником тепла в месте, задаваемом координатами (15,20) внутри этой области.Решение уравнения Пуассона с помощью функции relax
Листинг 13.7. Решение уравнения Пуассона с помощью функции relax
Первые три строки имеют тот же смысл, что и в предыдущем листинге. Только вместо одного источника тепла взято их другое распределение — один сильный источник, один более слабый и один сток тепла. В следующих шести строках задаются коэффициенты разностной схемы. Отложим их обсуждение до последнего раздела этой главы, ограничившись утверждением, что для решения уравнения Пуассона коэффициенты должны быть взяты именно такими, как показано в листинге 13.7. В предпоследней строке задана матрица нулевых граничных условий и нулевых начальных приближений, а в последней матрице G присваивается результат действия функции relax. График полученного решения в виде линий уровня показан на рис. 13.18.
Решение уравнения теплопроводности при помощи функции relax
Листинг 13.8. Решение уравнения теплопроводности при помощи функции relax
Результат действия программы листинга 13.8 показан на рис. 13.20 в виде трехмерной "поверхности. Если сравнить рис. 13.20 с рис. 13.4, полученным при расчетах по запрограммированной разностной схеме, то в графиках рис. 13.4 нетрудно узнать сечения этой поверхности плоскостями t=const. Еще раз подчеркнем, что использовать встроенную функцию можно только для тех уравнений, которые допускают построение разностной схемы типа "крест" (см. рис. 13.16) или составного фрагмента этой схемы.
Матрица системы линейных разностных уравнений для неявной схемы (листинг 13.2 для М=10)
Матрица системы линейных разностных уравнений для неявной схемы (листинг 13.2 для М=10)
Нелинейное уравнение
Нелинейное уравнениеНамного более интересные решения можно получить для нелинейного уравнения теплопроводности, например с нелинейным источником тепла Ф(u)=103(u-u3). Заметим, что в листинге 13.1 мы предусмотрительно определили коэффициент диффузии и источник тепла в виде пользовательских функций, зависящих от аргумента и, т. е. от температуры (если бы собирались моделировать явную зависимость их от координат, то следует ввести в пользовательскую функцию в качестве аргумента переменную х, как это сделано для источника тепла ф). Поэтому нет ничего проще замены определения этих функций с констант D(u)=1 и ф(х,u)=0 на новые функции, которые станут описывать другие модели диффузии тепла. Начнем с того, что поменяем четвертую строку листинга 13.1 на ф(х,u)=103(u-u3), не изменяя пока постоянного значения коэффициента диффузии.
С физической точки зрения зависимость коэффициента диффузии и функции источника тепла от температуры означает, что эти параметры будут меняться от точки к точке среды, определяясь локальными значениями текущей температуры в этих точках. Ввод ненулевого источника тепла означает, что среда получает определенное количество тепла, тем большее, чем больше локальная температура. Можно догадаться, что введение такой зависимости может моделировать, в частности, горение среды.
Если осуществить расчеты с упомянутым источником (имеющим кубическую нелинейность), то получится очень интересное решение уравнения теплопроводности, имеющее профиль тепловых фронтов. С течением времени граница раздела высокой и низкой температуры распространяется в обе стороны от зоны первичного нагрева, оставаясь весьма четко выделенной (рис. 13.8).
Еще более неожиданные решения возможны при нелинейности также и коэффициента диффузии. Например, если взять квадратичный коэффициент диффузии D(x,u)=u2 (что с учетом его умножения на неизвестные функции создаст кубическую нелинейность уравнения), а также ф(х,u)=103u3 5, то Вы сможете наблюдать совсем иной режим горения среды. В отличие от рассмотренного эффекта распространения тепловых фронтов, горение оказывается локализованным в области первичного нагрева среды, причем, температура в центре нагрева со временем возрастает до бесконечной величины (рис. 13.9). Такое решение описывает так называемый режим горения "с обострением".
Обратное уравнение теплопроводности
Обратное уравнение теплопроводностиЗамечательными свойствами обладает так называемое обратное уравнение диффузии тепла, которое получается путем замены в исходном (прямом) уравнении переменной t на -t. Согласно постановке задачи, обратное уравнение теплопроводности описывает реконструкцию динамики профиля температуры остывающего стержня, если известно начальное условие в виде профиля температуры в некоторый момент времени после начала остывания. Таким образом, требуется определить, как происходило остывание стержня. Мы ограничимся самым простым линейным уравнением с D=const без источников тепла:
Это уравнение гиперболического типа и оно, несмотря на кажущуюся близость к рассмотренным вариантам уравнения теплопроводности, обладает весьма замечательными свойствами.
Если попробовать осуществить расчет обратного уравнения диффузии тепла по тем же самым алгоритмам, что и для обычных уравнений (для этого достаточно в листинге 13.1 или 13.2 заменить значение коэффициента диффузии на отрицательное число, например D=-1), то мы получим заведомо нефизичное решение. Оно показано на рис. 13.5 в виде профилей распределения температуры для нескольких последовательных моментов времени. Как видно, решение выражается в появлении все более быстрых пространственных осцилляции профиля температуры для каждого нового момента времени. Очень существенно, что такое поведение решение является не проявлением неустойчивости численного алгоритма (см. разд. "Устойчивость" этой главы), а определяется спецификой самой задачи.
Оказывается, что обратное уравнение теплопроводности принадлежит к довольно широкому классу задач, называемых некорректными. Некорректные задачи нельзя решать стандартными методами, а для того чтобы с ними справиться (т. е., чтобы получить осмысленное физическое решение) приходится несколько менять саму их постановку, вводя в нее дополнительную априорную информацию о строении решения.

Численное решение обратного уравнения теплопроводности дает совершенно нефизичную картину динамики температуры (см. листинги 13.1, 2 ниже с параметром D=-1)
Одномерное динамическое уравнение
Одномерное динамическое уравнениеПредположим, что мы рассматриваем задачу распределения тепла не по плоской поверхности, а по удлиненному телу типа металлического стержня (рис. 13.3). В этом случае зависимость от координаты у в общем уравнении теплопроводности пропадает, и получается одномерное уравнение:
Построение неявной разностной схемы
Построение неявной разностной схемыЧтобы построить неявную разностную схему для уравнения диффузии, используем шаблон, изображенный на рис. 13.11, т. е. для дискретизации пространственной производной будем брать значения сеточной функции с верхнего (неизвестного) слоя по времени. Таким образом, разностное уравнение для (i,k)-ro узла будет отличаться от уравнения для явной схемы (8) только индексами по временной координате в правой части:
Построение разностной схемы
Построение разностной схемыИспользуем для решения уравнения теплопроводности шаблон, изображенный на рис. 13.6. Для дискретизации второй производной по пространственной координате необходимо использовать три последовательных узла, в то время как для разностной записи первой производной по времени достаточно двух узлов. Записывая на основании данного шаблона дискретное представление для (i,k)-ro узла, получим разностное уравнение:
Разностная схема для решения уравнения Пуассона
Разностная схема для решения уравнения ПуассонаНесмотря на отсутствие сведений в справочной системе Mathcad о решении других линейных дифференциальных уравнений в частных производных, кроме уравнения Пуассона, сделать это возможно с помощью той же функции relax (см. предыдущий разд.). Для этого нужно правильным образом задать коэффициенты разностной схемы.
Начнем с пояснения выбора этих коэффициентов (см. листинг 13.7) для уравнения Пуассона. Согласно основным идеям метода сеток (см. разд. "Разностные схемы" этой главы), для дискретизации обеих пространственных производных в уравнении (12) следует использовать по три соседних узла вдоль каждой из координат. Поэтому уравнение Пуассона (12) может быть записано в разностной форме при помощи шаблона типа "крест" (рис. 13.19). В этом случае после приведения подобных слагаемых в разностных уравнениях коэффициенты разностной схемы будут такими, как показано возле узлов шаблона на этом рисунке (аналогичные коэффициенты для явной и неявных схем решения уравнения теплопроводности см. на рис. 13.6 и 13.11, соответственно).
Теперь если Вы сравните полученные числа с константами, которые присвоены элементам матриц-аргументов функции relax (см. листинг 13.7), то увидите, что они как раз и описывают вычисленные нами только что коэффициенты разностной схемы "крест". Таким образом, нетрудно сообразить, что с помощью встроенной функции relax можно решать и другие линейные дифференциальные уравнения в частных производных, которые можно аппроксимировать схемой типа "крест" или схемой, являющейся ее составной частью. Конечно, для того чтобы использовать эту встроенную функцию для другого уравнения, необходимо будет составить соответствующую разностную схему.
Решение линейного уравнения теплопроводности...
Решение линейного уравнения теплопроводности при помощи неявной схемы на первом слое по времени (листинг 13.2)
Для отыскания решения линейных систем алгебраических уравнений имеется чрезвычайно эффективный алгоритм, называемый прогонкой, который позволяет снизить число арифметических операций на целый порядок, т. е. до значения порядка м. Это означает, что при использовании пространственных сеток с юоо узлами выигрыш во времени вычислений составит величину порядка 103! Реализация данного алгоритма приведена в листинге 13.3, который является продолжением листинга 13.2, используя определенные в нем коэффициенты матрицы А, а также начальное условие.
Программа листинга 13.3 осуществляет пересчет одного шага по времени, т. е. заменяет содержимое столбца и с предыдущего временного слоя вычисленными значениями неизвестной функции со следующего слоя. Первые пять строк листинга 13.3 представляют так называемый обратный ход прогонки, а последние две строки - ее прямой ход. Заинтересовавшемуся читателю предлагается самому оформить представленный алгоритм прогонки в виде программы решения разностных уравнений для вычисления произвольного временного слоя по примеру листингов 13.1 и 13.2. Заметим, что описание этого знаменитого алгоритма можно отыскать практически в любом современном учебнике по численным методам.
Решение линейного уравнения теплопроводности (листинг 13.1)
Решение линейного уравнения теплопроводности (листинг 13.1)
Начальное распределение температуры вдоль расчетной области и решение для двух моментов времени показано на рис. 13.7 сплошной, пунктирной и штриховой линиями, соответственно. Физически такое поведение вполне естественно — с течением времени тепло из более нагретой области перетекает в менее нагретую, а зона изначально высокой температуры остывает и размывается.
Решение одномерного уравнения теплопроводности (см. листинг 13.1 ниже)
Решение одномерного уравнения теплопроводности (см. листинг 13.1 ниже)
Решение линейных уравнений в частных производных, как правило, получаются вполне предсказуемыми и их часто можно получить аналитически (этим проблемам посвящены соответствующие главы науки, называемой математической физикой). В случае уравнения теплопроводности линейная задача описывает физически ожидаемое решение, выражающее остывание пластины или стержня в форме перетекания тепла от нагретого центра к холодной периферии.
Нелинейные уравнения, напротив, могут демонстрировать самые неожиданные решения, причем в подавляющем большинстве практических задач их можно получить только численно, а никак не аналитически.
Различные линейные и нелинейные варианты рассматриваемого уравнения теплопроводности описывают различные модели физических сред, которые характеризуются определенными зависимостями D(u) и ф(и). В частности, для металлов в большинстве случаев можно считать, что D=const, в то время как для плазмы имеется специфическая зависимость коэффициента диффузии от температуры.
Решение стационарного двумерного уравнения теплопроводности (см. листинг 13.7 ниже)
Решение стационарного двумерного уравнения теплопроводности (см. листинг 13.7 ниже)
Как несложно сообразить, если искомая функция не зависит от времени, то частная производная по времени в левой части уравнения равна нулю, и само уравнение можно переписать (переобозначив ради упрощения) следующим образом:
Полученное уравнение, согласно классификации предыдущего раздела, является эллиптическим. Его называют уравнением Пуассона, а для его решения в Mathcad предусмотрены две встроенные функции. Если, к тому же, источники равны нулю, то уравнение, принимающее вид du=0, называют уравнением Лапласа.
Решение уравнения диффузии тепла при помощи функции relax
Решение уравнения диффузии тепла при помощи функции relaxПриведем пример применения встроенной функции relax для решения другого уравнения в частных производных (т. е. не уравнения Пуассона, для которого она изначально предназначена). Вычислим при помощи этой функции решение уже хорошо нам знакомого однородного линейного уравнения теплопроводности (см. разд. 13.1.2). Будем использовать явную разностную схему, шаблон которой изображен на рис. 13.6. Для того чтобы "приспособить" для явной схемы функцию relax, требуется только задать ее аргументы в соответствии с коэффициентами, показанными на шаблоне (см. тот же рис. 13.6). Программа, реализующая таким способом явную схему, представлена на листинге 13.8. Число Куранта в этом листинге обозначено переменной с, как и положено явной разностной схеме, она выдает устойчивое решение только для C<1.
Решение уравнения диффузии тепла при помощи встроенной функции Pdesolve (листинг 13.4)
Решение уравнения диффузии тепла при помощи встроенной функции Pdesolve (листинг 13.4)
Здесь неизвестная функция u(x,t) описывает динамику смещения профиля струны относительно невозмущенного (прямолинейного) положения, а параметр с характеризует материал, из которого изготовлена струна.
Как Вы видите, уравнение (11) содержит производные второго порядка как по пространственной координате, так и по времени. Для того чтобы можно было использовать встроенную функцию pdesoive, необходимо переписать волновое уравнение в виде системы двух уравнений в частных производных, введя вторую неизвестную функцию v=ut. Программа для решения волнового уравнения приведена в листинге 13.5, а результат — на рис. 13.15.
Решение уравнения Пуассона с помощью функции relax (листинг 13.7)
Решение уравнения Пуассона с помощью функции relax (листинг 13.7)
Решение уравнения теплопроводности...
Решение уравнения теплопроводности с нелинейным источником и коэффициентом диффузии (режим локализации горения)
Решение уравнения теплопроводности с нелинейным источником (тепловой фронт)
Решение уравнения теплопроводности с нелинейным источником (тепловой фронт)
Читателю предлагается поэкспериментировать с этим и другими нелинейными вариантами уравнения теплопроводности. Существенно, что такие интересные результаты удается получить лишь численно, а в Mathcad только с применением элементов программирования.
Решение уравнения теплопроводности с помощью функции relax (листинг 13.8)
Решение уравнения теплопроводности с помощью функции relax (листинг 13.8)
В заключение разговора об уравнениях в частных производных, нельзя не сказать несколько слов об их визуализации. Результат решения динамических уравнений (зависящих от времени t) выглядит намного эффектнее, если будет представлен в виде анимации. Для создания анимационных роликов расчетное время следует выразить через константу FRAME и затем применить команду View / Animate (Вид / Анимация) (как об этом рассказано в разд. "Создание анимации" гл. 16).
Решение волнового уравнения (листинг 13.5)
Решение волнового уравнения (листинг 13.5)
Шаблон аппроксимации уравнения Пуассона "крест"
Шаблон аппроксимации уравнения Пуассона "крест"
Шаблон аппроксимации явной схемы для уравнения теплопроводности
Шаблон аппроксимации явной схемы для уравнения теплопроводности
Приведем в разностной схеме (8) подобные слагаемые, перенеся в правую часть значения сеточной функции с индексом k (как часто говорят, с предыдущего слоя по времени), а в левую - с индексом k-t-i (т. е. со следующего временного слоя). Кроме этого, введем коэффициент с , который будет характеризовать отношение шагов разностной схемы по времени и пространству Несколько забегая вперед, заметим, что значение параметра с, называемого коэффициентом Куранта, имеет большое значение для анализа устойчивости разностной схемы. С учетом этих замечаний, разностная схема (8) запишется в виде: Множители для каждого из значений сеточной функции в узлах шаблона, соответствующие разностному уравнению (9), приведены рядом с каждой точкой шаблона на рис. 13.6. Фактически, геометрия шаблона и эти множители задают построенную нами разностную схему.
Несложно убедиться в том, что для получения замкнутой системы разностных алгебраических уравнений систему (9) необходимо дополнить дискретным представлением начального и граничных условий (6) и (7). Тогда число неизвестных будет в точности равно числу уравнений, и процесс формирования разностной схемы будет окончательно завершен.
Важно подчеркнуть, что возможная нелинейность полученной системы алгебраических уравнений определяется зависимостями от температуры функций D(u) и ф(и), т. е. как коэффициент диффузии, так и источник тепла могут быть функциями сеточной функции uik.
Если присмотреться к разностным уравнениям (9) повнимательнее, то можно сразу предложить несложный алгоритм реализации этой разностной схемы. Действительно, каждое неизвестное значение сеточной функции со следующего временного слоя, т. е. левая часть соотношения (9) явно выражается через три ее значения с предыдущего слоя (правая часть), которые уже известны. Таким образом, в случае уравнения теплопроводности нам очень повезло — для расчета 1-го слоя по времени следует попросту подставить в (9) начальное условие (известные значения и с нулевого слоя в узлах сетки), для расчета 2-го слоя достаточно использовать вычисленный таким образом набор и с 1-го слоя и т. д. Из-за того, что разностная схема сводится к такой явной подстановке, ее и называют явной, а благодаря пересчету значений с текущего слоя через ранее вычисленные слои — схемой бегущего счета.
Шаблон неявной схемы для уравнения теплопроводности
Шаблон неявной схемы для уравнения теплопроводности
Если привести подобные слагаемые, то получится система уравнений, связывающая для каждого 1-го узла три неизвестных значения сеточной функции (в самом этом узле и в соседних с ним слева и справа узлах). Множители при неизвестных значениях сеточной функции в узлах шаблона показаны на рис. 13.11 в виде подписей, подобно тому как это было сделано для явной схемы (см. рис. 13.6).
Очень важно, что если само уравнение теплопроводности линейно, то с в левой части разностного уравнения является константой, а ф в его правой части может зависеть только от первой степени и. Поэтому система уравнений (10) для всех пространственных узлов 1=1...м-1 является линейной системой, что существенно упрощает ее решение (поскольку известно, что для линейных систем с ненулевым определителем решение существует и является единственным). Напомним, что для получения замкнутой системы линейных уравнений необходимо дополнить данный набор разностных уравнений граничными условиями, т. е. известными значениями сеточной функции для 1=0 и i=M.
Если рассматривать нелинейный случай, то на каждом шаге по времени пришлось бы решать систему нелинейных уравнений, число решений которых могло бы быть большим, и среди них требовалось бы отыскать нужное, а не паразитное решение.
Для реализации неявной схемы, таким образом, можно использовать комбинацию средств программирования Mathcad и встроенной функции решения системы линейных уравнений isoive. Один из возможных способов решения предложен в листинге 13.2. Большая часть этого листинга является вводом параметров задачи (шагов, начальных и граничных условий), и только в последней его строке определяется функция пользователя, вычисляющая сеточную функцию на каждом временном слое (при помощи встроенной функции решения системы линейных уравнений isoive). В нескольких предыдущих строках листинга (после расчета коэффициента Куранта сои) формируется матрица системы уравнений А, которая записывается в подходящем для Mathcad виде, как это сделано в листинге 13.2. Как несложно убедиться, столбец правых частей разностных уравнений выражается вычисленными значениями сеточной функции с предыдущего слоя.
Результаты расчетов по неявной схеме показаны на рис. 13.12 и, как видно, они дают примерно те же результаты, что и в случае применения явной схемы (см. рис. 13.7). Обратите внимание, что решение устойчиво при любых значениях коэффициента Куранта (в том числе, и больших 1), поскольку, как следует из соответствующих положений теории численных методов, неявная схема является безусловно устойчивой.
Стационарное двумерное уравнение
Стационарное двумерное уравнениеЧастный случай уравнения теплопроводности определяет стационарную, т. е. не зависящую от времени задачу. Стационарное уравнение описывает физическую картину распределения температуры по пластине, не изменяющуюся с течением времени. Такая картина может возникнуть при условии, что стационарный источник тепла действует довольно продолжительное время, и переходные процессы, вызванные его включением, прекратились. Пример численного решения такого уравнения показан на рис. 13.2 в виде поверхности и (х,у).
Уравнение Пуассона с нулевыми граничными условиями
Уравнение Пуассона с нулевыми граничными условиямиКорректная постановка краевой задачи для уравнения Пуассона требует задания граничных условий. В Mathcad решение ищется на плоской квадратной области, состоящей из (м+1)х(м+1) точек. Поэтому граничные условия должны быть определены пользователем для всех четырех сторон упомянутого квадрата. Самый простой вариант — это нулевые граничные условия, т. е. постоянная температура по всему периметру расчетной области. В таком случае можно использовать встроенную функцию multigrid.
Параметр численного метода ncycie в большинстве случаев достаточно взять равным 2.
Уравнение Пуассона с произвольными граничными условиями
Уравнение Пуассона с произвольными граничными условиямиВ более сложных случаях, например для решения краевой задачи с ненулевыми условиями на границах, следует использовать другую встроенную функцию relax, имеющуюся в Mathcad.
Устойчивость
УстойчивостьКак мы убедились, явная разностная схема Эйлера дает вполне разумные результаты и вполне может использоваться для практического моделирования задач, связанных с решением уравнений в частных производных. Однако теперь пришло время сказать об очень важной характеристике разностных схем, которая называется их устойчивостью. Не вдаваясь в детали, заметим, что производить расчеты можно только при помощи устойчивых разностных схем, а чтобы пояснить это понятие, обратимся вновь к листингу 13.1, реализующему явную схему для линейного уравнения диффузии.
Слегка изменим соотношение шагов по времени и пространственной координате, произведя расчеты сначала с т=0.0005 (эти результаты показаны на рис. 137 выше) и также с т=0.0010 и т=0.0015. Результат применения разностной схемы Эйлера для т=0.0010 примерно тот же, что и для меньшего значения т, приведенного на рис. 13.7. А вот следующее (казалось бы, незначительное) увеличение шага по времени приводит к катастрофе (рис. 13.10). Вместо ожидаемого решения получается совершенно неожиданные профили температуры, которые быстро осциллируют вдоль пространственной координаты, причем амплитуда и число пиков этих осцилляции быстро увеличиваются от шага к шагу. Совершенно ясно, что полученное решение не имеет ничего общего с физикой моделируемого явления, а является следствием внутренних свойств самой разностной схемы, которые до этого были для нас скрыты.
Математический редактор MathCAD
Нормальное (Гауссово) распределение
14.1.1. Нормальное (Гауссово) распределениеВ теории вероятности доказано, что сумма различных независимых случайных слагаемых (независимо от их закона распределения) оказывается случайной величиной, распределенной согласно нормальному закону (т. н. центральная предельная теорема). Поэтому нормальное распределение хорошо моделирует самый широкий круг явлений, для которых известно, что на них влияют несколько независимых случайных факторов.
Перечислим встроенные функции, имеющиеся в Mathcad для описания нормального распределения вероятностей:
Равномерное распределение
14.1.2. Равномерное распределениеСамое простое распределение случайной величины — это распределение с постоянной вероятностью. Вероятность p=const=1/ (b-a) при хе(а,b) и P=0, для х вне интервала (а,Ь). Эту плотность вероятности, наряду с прочими статистическими характеристиками, задают следующие встроенные функции:
Биномиальное распределение
14.1.3. Биномиальное распределениеПриведем встроенные функции, описывающие еще одно распределение случайной величины, которая, в отличие от двух предыдущих, является не непрерывной, а может принимать лишь дискретные значения. Биномиальное распределение описывает последовательность независимых испытаний, каждое из которых может приводить к генерации определенного события с постоянной вероятностью р.
Другие статистические распределения
14.1.4. Другие статистические распределенияКак легко заметить по рассмотренным трем распределениям, Mathcad имеет четыре основные категории встроенных функций. Они различаются написанием их первой литеры, а оставшаяся часть имени функций (ниже в списке функций она условно обозначена звездочкой) идентифицирует тот или иной тип распределения.
Перечислим все типы распределения, реализованные в Mathcad, вместе с их параметрами, на этот раз обозначив звездочкой * недостающую первую букву встроенных функций. Некоторые из плотностей вероятности показаны на рис. 14.7.
Случайные величины
14.1. Случайные величиныДля моделирования различных физических, экономических и прочих эффектов широко распространены методы, называемые методами Монте-Карло. Их основная идея состоит в создании определенной последовательности случайных чисел, моделирующей тот или иной эффект, например, шум в физическом эксперименте, случайную динамику биржевых индексов и т. п. Для этих целей в Mathcad имеется ряд встроенных функций, реализующих различные типы генераторов псевдослучайных чисел.
Согласно определению, случайная величина принимает то или иное значение, но какое конкретно, зависит от случайных обстоятельств опыта и заранее точно предсказано быть не может. Можно лишь говорить о вероятности P(Xк) принятия случайной дискретной величиной того или иного значения хк, или о вероятности попадания непрерывной случайной величины в тот или иной числовой интервал (х,х+dх). Вероятность Р(ХК) или P(X) (dх), соответственно, может принимать значения от о (такое значение случайной величины совершенно невероятно) до i (случайная величина заведомо примет значение от х до х+dх). Соотношение Р(ХК) называют законом распределения случайной величины, а зависимость P(х) между возможными значениями непрерывной случайной величины и вероятностями попадания в их окрестность называется ее плотностью вероятности (probability density).
В Mathcad имеется ряд встроенных функций, задающих используемые в математической статистике законы распределения. Они вычисляют как значение плотности вероятности различных распределений по значению случайной величины х, так и некоторые сопутствующие функции. Все они, по сути, являются либо встроенными аналитическими зависимостями, либо специальными функциями. Большой интерес представляет наличие генераторов случайных чисел, создающих выборку псевдослучайных данных с соответствующим законом распределения. Рассмотрим подробно возможности Mathcad на нескольких наиболее популярных законах распределения, а затем приведем перечень всех распределений, встроенных в Mathcad.
Построение гистограмм
14.2.1. Построение гистограммГистограммой называется график, аппроксимирующий по случайным данным плотность их распределения. При построении гистограммы область значений случайной величины (а,b> разбивается на некоторое количество bin сегментов, а затем подсчитывается процент попадания данных в каждый сегмент. Для построения гистограмм в Mathcad имеется несколько встроенных функций. Рассмотрим их, начиная с самой сложной по применению, чтобы лучше разобраться в возможностях каждой из функций.
Среднее значение и дисперсия
14.2.2. Среднее значение и дисперсияВ Mathcad 11 имеется ряд встроенных функций для расчетов числовых статистических характеристик рядов случайных данных.
Генерация коррелированных случайных чисел
14.2.3. Генерация коррелированных случайных чиселДо сих пор мы рассматривали наиболее простой случай применения генераторов независимых случайных чисел. В методах Монте-Карло часто требуется создавать случайные числа с определенной корреляцией. Приведем пример программы, создающей два вектора x1 и х2 одинакового размера и одним и тем же распределением, случайные элементы которых попарно коррелированы с коэффициентом корреляции R (листинг 14.12).
Ковариация и корреляция
14.2.4. Ковариация и корреляцияФункции, устанавливающие связь между парами двух случайных векторов, называются ковариацией и корреляцией (или, по-другому, коэффициентом корреляции). Они различаются нормировкой, как следует из их определения (листинг 14.13).
Коэффициенты асимметрии и эксцесса
14.2.5. Коэффициенты асимметрии и эксцессаКоэффициент асимметрии задает степень асимметричности плотности вероятности относительно оси, проходящий через ее центр тяжести. Коэффициент асимметрии определяется третьим центральным моментом распределения. В любом симметричном распределении с нулевым математическим ожиданием, например нормальным, все нечетные моменты, в том числе и третий, равны нулю, поэтому коэффициент асимметрии тоже равен нулю.
Степень сглаженности плотности вероятности в окрестности главного максимума задается еще одной величиной — коэффициентом эксцесса. Он показывает, насколько острую вершину имеет плотность вероятности по сравнению с нормальным распределением. Если коэффициент эксцесса больше нуля, то распределение имеет более острую вершину, чем распределение Гаусса, если меньше нуля, то более плоскую.
Для расчета коэффициентов асимметрии и эксцесса в Mathcad имеются две встроенные функции.
Другие статистические характеристики
14.2.6. Другие статистические характеристикиВ предыдущих разделах были рассмотрены встроенные функции, рассчитывающие наиболее часто используемые статистические характеристики выборок случайных данных. Иногда в статистике встречаются и иные функции, например, помимо арифметического среднего, применяются другие средние значения.
Действие статистических функций на матрицы
14.2.7. Действие статистических функций на матрицыВсе рассмотренные примеры работы статистических функций относились к векторам, элементы которых были случайными числами. Но точно так же все эти функции применяются и по отношению к выборкам случайных данных, сгруппированных в матрицы. При этом статистические характеристики рассчитываются для совокупности всех элементов матрицы, без разделения ее на строки и столбцы. Например, если матрица имеет размерность MXN, то и объем выборки будет равен M-N.
Соответствующий пример вычисления среднего значения приведен в листинге 14.16. В его первой строке определяется матрица данных х размера 4x2. Действие встроенной функции mean матричного аргумента (последняя строка листинга) иллюстрируется явным суммированием элементов матрицы х (предпоследняя строка). Действие прочих встроенных функций на матрицы совершенно аналогично действию их на векторы (листинг 14.17).
Статистические характеристики
14.2. Статистические характеристикиВ большинстве статистических расчетов Вы имеете дело либо со случайными данными, полученными в ходе какого-либо эксперимента (которые выводятся из файла или печатаются непосредственно в документе), либо с результатами генерации случайных чисел, рассмотренными в предыдущих разделах встроенными функциями, моделирующими то или иное явление методом Монте-Карло. Рассмотрим возможности Mathcad по оценке функций распределения и расчету числовых характеристик случайных данных.
Случайные процессы
14.3. Случайные процессыВстроенные функции для генерации случайных чисел создают выборку из случайных данных АХ. Часто требуется создать непрерывную или дискретную случайную функцию A(t) одной или нескольких переменных (случайный процесс или случайное поле), значения которой будут упорядочены относительно своих переменных Создать псевдослучайный процесс можно способом, представленным в листинге 14 19
Интервальная оценка дисперсии
14.4.1. Интервальная оценка дисперсииТребуется определить числовой интервал (L,U), внутри которого будет лежать с вероятностью 1-сс=75% дисперсия нормальной случайной величины, исходя из объема выборки в N чисел. Эта задача решается в статистике с помощью х2-распределения (листинг 14.21).
Проверка статистических гипотез
14.4.2. Проверка статистических гипотезВ статистике рассматривается огромное число задач, связанных с проверкой тех или иных гипотез н. Разберем пример простой гипотезы. Пусть имеется выборка N чисел с нормальным законом распределения и неизвестными дисперсией и математическим ожиданием. Требуется принять или отвергнуть гипотезу н о том, что математическое ожидание закона распределения равно некоторому числу m0=0.2.
Задачи проверки гипотез требуют задания уровня критерия проверки гипотезы а, который описывает вероятность ошибочного отклонения истинной н. Если взять а очень малым, то гипотеза, даже если она ложная, будет почти всегда приниматься; если, напротив, взять а близким к 1, то критерий будет очень строгим, и гипотеза, даже верная, скорее всего, будет отклонена. В нашем случае гипотеза состоит в том, что цо=о.2, а альтернатива — что m0=0.2. Оценка математического ожидания, как следует из курса классической статистики, решается с помощью распределения Стьюдента с параметром N-1 (этот параметр называется степенью свободы распределения).
Для проверки гипотезы (листинг 14.22) рассчитывается (а/2) — квантиль распределения Стьюдента т, который служит критическим значением для принятия или отклонения гипотезы. Если соответствующее выборочное значение t по модулю меньше т, то гипотеза принимается (считается верной). В противном случае гипотезу следует отвергнуть.
Диалоговое окно Insert Function
Диалоговое окно Insert Function
Гистограмма распределения Вейбулла (листинг 14.10)
Гистограмма распределения Вейбулла (листинг 14.10)
Определение статистических характеристик случайных величин приведено в листинге 14.11 на еще одном примере обработки выборки малого объема (по пяти данным). В том же листинге иллюстрируется применение еще двух функций, которые имеют смысл дисперсии и стандартного отклонения в несколько другой нормировке. Сравнивая различные выражения, Вы без труда освоите связь между встроенными функциями.
Осторожно относитесь к написанию первой литеры в этих функциях, особенно при обработке малых выборок (листинг 14.11).
Гистограмма с произвольными сегментами разбиения
Гистограмма с произвольными сегментами разбиенияГистограмма с разбиением на равные сегменты
Гистограмма с разбиением на равные сегментыЕсли нет необходимости задавать сегменты гистограммы разной ширины, то удобнее воспользоваться упрощенным вариантом функции hist.
Недостаток упрощенной формы функции hist в том, что по-прежнему необходимо дополнительно определять вектор сегментов построения гистограммы. От этого недостатка свободна появившаяся в Mathcad 2001 функция histogram.
График и матрица гистограммы (листинг 14.9)
График и матрица гистограммы (листинг 14.9)
Корреляционная функция (листинги 14.19—14.20)
Корреляционная функция (листинги 14.19—14.20)
К задаче проверки статистических гипотез (листинг 14.22)
К задаче проверки статистических гипотез (листинг 14.22)
Расчет числовых характеристик случайного вектора
Листинг 14.10. Расчет числовых характеристик случайного вектора
На рис. 14.12 приведена гистограмма выборки случайных чисел, распределенных согласно закону Вейбулла. Пунктирные вертикальные прямые, показанные на графике, рассчитаны в последней строке листинга и обозначают стандартное отклонение от среднего значения. Гистограмма получена с помощью листинга 14.8, рассмотренного в предыдущем разделе. Обратите внимание, что поскольку распределение Вейбулла, в отличие, например, от Гауссова, несимметричное, то медиана не совпадает со средним значением.
Копределению статических характеристик
Листинг 14.11. Копределению статических характеристик
Генерация попарно коррелированных случайных чисел
Листинг 14.12. Генерация попарно коррелированных случайных чисел
Результат действия программы для R=0.4 показан на рис. 14.13 (слева). Сравните полученную выборку с правым графиком, полученным для высокой корреляции (R=0.9) и с рис. 14.3 (см. разд. 14.1.1) для независимых данных, т. е. R=0.
Расчет ковариации и корреляции (продолжение листинга 14.12)
Листинг 14.13. Расчет ковариации и корреляции (продолжение листинга 14.12)
Расчет выборочных коэффициентов асимметрии и экспресса
Листинг 14.14. Расчет выборочных коэффициентов асимметрии и экспресса
Вычисление различных средних значений
Листинг 14.15. Вычисление различных средних значений
Вычисление среднего значения элементов матрицы
Листинг 14.16. Вычисление среднего значения элементов матрицы
Действие различных статических функций на матрицу
Листинг 14.17. Действие различных статических функций на матрицу
Некоторые статистические функции (например, вычисления ковариации) имеют два аргумента. Они также могут быть матрицами, но, в соответствии со смыслом функции, должны иметь одинаковую размерность.
Большинству статистических функций позволяется иметь в качестве аргументов даже не одну матрицу, а любое количество матриц, векторов и скаляров. Числовые характеристики будут рассчитаны для всей совокупности значений аргументов функции. Соответствующий пример приведен в листинге 14.18.
Статические функции нескольких аргументов
Листинг 14.18. Статические функции нескольких аргументов
Генерация псевдослучайного процесса
Листинг 14.19. Генерация псевдослучайного процесса
В первой строке листинга 14 19 определено количество N независимых случайных чисел, которые будут впоследствии сгенерированы, и радиус временной корреляции т В следующих трех строках определяются моменты времени тэ, которым будут отвечать случайные значения A(t.,) Создание нормального случайного процесса сводится к генерации обычным способом вектора независимых случайных чисел х и построению интерполяционной зависимости в промежутках между ними В листинге 14 19 используется сплайн-интерполяция (см гл 15)
Вероятность того, что
Листинг 14.1. Вероятность того, что х будет меньше 1.881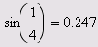
Дискретизация случайного...
Листинг 14.20. Дискретизация случайного процесса и вычисление корреляционной функции (продолжение листинга 14.19)
Дискретизация интервала <0,Tmax) для случайного процесса A(t) произведена с различным элементарным интервалом А (первая строка листинга). В зависимости от значения А, получается различный объем п выборки случайных чисел YL являющихся значениями случайной функции A(t) в точках дискретизации. В последних четырех строках определяются различные характеристики случайной величины Y, являющиеся, по сути, характеристиками случайного процесса A(t). График рассчитанной в 2 M+1 точках корреляционной функции R(j) показан на рис. 14.15.
Внимательному читателю предлагается самостоятельно ответить на вопрос: почему при таком расчете корреляционной функции ее значение R(0) не равно 1, как должно быть по определению?
доверительным интервалом. Обратите внимание на
Листинг 14.21. Интервальное оценивание дисперсии 1
Указанный интервал называется (1-а)% доверительным интервалом. Обратите внимание на использование при решении данной задачи функции stdev (с прописной буквы) для расчета выборочного стандартного отклонения. В статистике часто встречаются выражения, которые более удобно записывать через функции в такой нормировке, именно для этого они и появились в Mathcad.
Проверка гипотезы о математическом ожидании при неизвестной дисперсии
Листинг 14.22. Проверка гипотезы о математическом ожидании при неизвестной дисперсии
В последней строке листинга вычисляется истинность или ложность условия, выражающего решение задачи. Поскольку условие оказалось ложным (равным не 1, а 0), то гипотезу необходимо отвергнуть.
На рис. 14.16 показано распределение Стьюдента с N-1 степенью свободы вместе с критическими значениями, определяющими соответствующий интервал. Если t (оно тоже показано на графике) попадает в него, то гипотеза принимается; если не попадает (как произошло в данном случае) — отвергается. Если увеличить а, ужесточив критерий, то границы интервала будут сужаться, по сравнению с показанными на рисунке.
В листинге 14.23 приводится альтернативный способ проверки той же самой гипотезы, связанный с вычислением значения не квантиля, а самого распределения Стьюдента.
Другой вариант проверки гипотезы (продолжение листинга 14.22)
Листинг 14.23. Другой вариант проверки гипотезы (продолжение листинга 14.22)
Мы разобрали только два характерных примера статистических вычислений. Однако с помощью Mathcad легко решаются самые разнообразные задачи математической статистики.
Большое количество задач разобрано в Ресурсах в рубрике Statistics (Статистика) справочной системы Mathcad 11.
ный квантиль нормального распределения
Листинг 14.2. 97%-ный квантиль нормального распределения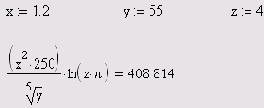
Вероятность того, что
Листинг 14.3. Вероятность того, что х будет больше 2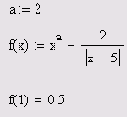
Вероятность того, что ж будет находиться в интервале (2,3)
Листинг 14.4. Вероятность того, что ж будет находиться в интервале (2,3)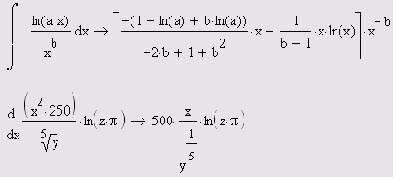
Обратите внимание, что задачи двух
Листинг 14.5. Вероятность того, что | х|<2
Обратите внимание, что задачи двух последних листингов решаются двумя разными способами. Второй из них связан с еще одной встроенной функцией erf, называемой функцией ошибок (или интегралом вероятности, или функцией Крампа).
Вероятность того, чтохбудвтвинтврвалв (2,3)
Листинг 14.6. Вероятность того, чтохбудвтвинтврвалв (2,3)
Если Вы имеете дело с моделированием методами Монте-Карло, то в качестве генератора случайных чисел с нормальным законом распределения применяйте встроенную функцию топа. В листинге 14.7 ее действие показано на примере создания двух векторов по M=500 элементов в каждом с независимыми псевдослучайными числами xLi и х2i распределенными согласно нормальному закону. О характере распределения случайных элементов векторов можно судить по рис. 14.3. В дальнейшем мы будем часто сталкиваться с генерацией случайных чисел и расчетом их различных средних характеристик.
Генерация двух векторов с нормальным законом распределения
Листинг 14.7. Генерация двух векторов с нормальным законом распределения
Построение гистограммы
Листинг 14.8. Построение гистограммы
Для анализа взято N=1000 данных с нормальным законом распределения, созданных генератором случайных чисел (третья строка листинга). Далее определяются границы интервала (upper,lower), содержащего внутри себя все случайные значения, и осуществляется его разбиение на количество (bin) одинаковых сегментов, начальные точки которых записываются в вектор int (предпоследняя строка листинга).
В векторе int можно задать произвольные границы сегментов разбиения так, чтобы они имели разную ширину.
Нормальные функции распределения
Нормальные функции распределения
Плотность вероятности биномиального распределения
Плотность вероятности биномиального распределения
Плотность вероятности и функция равномерного распределения
Плотность вероятности и функция равномерного распределения
Плотность вероятности некоторых распределений
Плотность вероятности некоторых распределений
Плотность вероятности нормальных распределений
Плотность вероятности нормальных распределений
Функция распределения F(X) (cumulative probability) — это вероятность того, что случайная величина примет значение меньшее или равное х. Как следует из математического смысла, она является интегралом от плотности вероятности в пределах от -x до х. Функции распределения для упомянутых нормальных законов изображены на рис. 14.2. Функция, обратная F(X) (inverse cumulative probability), называемая еще квантилем распределения, позволяет по заданному аргументу р определить значение х, причем случайная величина будет меньше или равна х с вероятностью р.
Здесь и далее графики различных статистических функций, показанные на рисунках, получены с помощью Mathcad без каких-либо дополнительных выражений в рабочей области.
Приведем несколько примеров, позволяющих почувствовать математический смысл рассмотренных функций на примере случайной величины х, распределенной по нормальному закону с m=0 и o=1 (листинги 14.1—14.5).
Построение гистограммы (листинг 14.8)
Построение гистограммы (листинг 14.8)
Обратите внимание, что в последней строке листинга осуществлена нормировка значений гистограммы, с тем чтобы она правильно аппроксимировала плотность вероятности, также показанную на графике. Очень важно переопределение вектора int в самом верху рис. 14.9, которое необходимо для перехода от левой границы каждого элементарного сегмента к его центру.
Псевдослучайные числа
Псевдослучайные числа с корреляцией R=0.4 (листинг 14.12) и R=0.9
Псевдослучайные числа с нормальным законом распределения (листинг 14.7)
Псевдослучайные числа с нормальным законом распределения (листинг 14.7)
Псевдослучайные числа с равномерным законом распределения
Псевдослучайные числа с равномерным законом распределения
Чаще всего в несложных программах применяется последняя функция, которая приводит к генерации одного псевдослучайного числа. Наличие такой встроенной функции в Mathcad — дань традиции, применяемой в большинстве сред программирования. Пример использования генератора вектора из м случайных чисел показан на рис. 14.4, который получен заменой в двух последних строках листинга 14.7 генератора нормальных чисел на runif (м,о, 1). Плотность вероятности и функция равномерного распределения показаны на рис. 14.5.
Псевдослучайный процесс (листинг 14.19)
Псевдослучайный процесс (листинг 14.19)
В результате получается случайный процесс A(t), радиус корреляции которого определяется расстоянием т между точками, для которых строится интерполяция. График случайного процесса A(t) вместе с исходными случайными числами показан на рис. 14.14. Случайное поле можно создать несколько более сложным способом с помощью многомерной интерполяции.
К случайным процессам, сгенерированным таким способом, как и к данным эксперимента, применяются любые статистические методы обработки, например корреляционный или спектральный анализ. Приведем в качестве примера листинг 14.20, показывающий, как организовать расчет корреляционной функции случайного процесса.
Создание графика гистограммы
Создание графика гистограммыДля того чтобы создать график в виде гистограммы:
Установка типа графика для построения гистограммы
Установка типа графика для построения гистограммы
Линейная интерполяция
15.1.1. Линейная интерполяцияСамый простой вид интерполяции — линейная, которая представляет искомую зависимость А(Х) в виде ломаной линии. Интерполирующая функция А(Х) состоит из отрезков прямых, соединяющих точки (рис. 15.2).
Кубическая сплайн-интерполяция
15.1.2. Кубическая сплайн-интерполяцияВ большинстве практических приложений желательно соединить экспериментальные точки не ломаной линией, а гладкой кривой. Лучше всего для этих целей подходит интерполяция кубическими сплайнами, т. е. отрезками кубических парабол (рис. 15.4).
Полиномиальная сплайн-интерполяция
15.1.3. Полиномиальная сплайн-интерполяцияБолее сложный тип интерполяции — так называемая интерполяция В-сплай-нами. В отличие от обычной сплайн-интерполяции (см. разд. 15.1.2), сшивка элементарных В-сплайнов производится не в точках хi а в других точках ui, координаты которых предлагается ввести пользователю. Сплайны могут быть полиномами 1, 2 или 3 степени (линейные, квадратичные или кубические). Применяется интерполяция В-сплайнами точно так же, как и обычная сплайн-интерполяция, различие состоит только в определении вспомогательной функции коэффициентов сплайна.
Интерполяция В-сплайнами иллюстрируется листингом 15.3 и рис. 15.7.
Экстраполяция функцией предсказания
15.1.4. Экстраполяция функцией предсказанияВсе рассмотренные выше (см. разд. 15.1.1—15.1.3) функции осуществляли экстраполяцию данных за пределами их интервала с помощью соответствующей зависимости, основанной на анализе расположения нескольких исходных точек на границах интервала. В Mathcad имеется более развитый инструмент экстраполяции, который учитывает распределение данных вдоль всего интервала. В функцию predict встроен линейный алгоритм предсказания поведения функции, основанный на анализе, в том числе осцилляции.
Многомерная интерполяция
15.1.5. Многомерная интерполяцияДвумерная сплайн-интерполяция приводит к построению поверхности z(x,y), проходящей через массив точек, описывающий сетку на координатной плоскости (х,у). Поверхность создается участками двумерных кубических сплайнов, являющихся функциями (х,у) и имеющих непрерывные первые и вторые производные по обеим координатам.
Многомерная интерполяция строится с помощью тех же встроенных функций, что и одномерная (см. разд. 15.1.2), но имеет в качестве аргументов не векторы, а соответствующие матрицы. Существует одно важное ограничение, связанное с возможностью интерполяции только квадратных NXN массивов данных.
Пример исходных данных приведен на рис. 15.10 в виде графика линий уровня, программная реализация двумерной интерполяции показана в листинге 15.6, а ее результат — на рис. 15.11.
Интерполяция
15.1. ИнтерполяцияКогда Вы имеете дело с выборкой экспериментальных данных, то они, чаще всего, представляются в виде массива, состоящего из пар чисел (xi, yi). Поэтому возникает задача аппроксимации дискретной зависимости y(xj непрерывной функцией f(x). Функция f(x), в зависимости от специфики задачи, может отвечать различным требованиям:
Линейная регрессия
15.2.1. Линейная регрессияСамый простой и наиболее часто используемый вид регрессии — линейная. Приближение данных (xi, yi) осуществляется линейной функцией у(х)=b+ах. На координатной плоскости (х,у) линейная функция, как известно, представляется прямой линией (рис. 15.12). Еще линейную регрессию часто называют методом наименьших квадратов, поскольку коэффициенты а и ь вычисляются из условия минимизации суммы квадратов ошибок |b+axi-yi|.
Чаще всего такое же условие ставится и в других задачах регрессии, т. е. приближения массива данных (хi,уi) другими зависимостями у(х). Исключение рассмотрено в листинге 15.9.
Полиномиальная регрессия
15.2.2. Полиномиальная регрессияВ Mathcad реализована регрессия одним полиномом, отрезками нескольких полиномов, а также двумерная регрессия массива данных.
Регрессия специального вида
15.2.3. Регрессия специального видаКроме рассмотренных, в Mathcad встроено еще несколько видов трехпара-метрической регрессии. Их реализация несколько отличается от приведенных выше вариантов регрессии тем, что для них, помимо массива данных, требуется задать некоторые начальные значения коэффициентов а,ь,с. Используйте соответствующий вид регрессии, если хорошо представляете себе, какой зависимостью описывается Ваш массив данных. Когда тип регрессии плохо отражает последовательность данных, то ее результат часто бывает неудовлетворительным и даже сильно различающимся в зависимости от выбора начальных значений. Каждая из функций выдает вектор уточненных параметров а,b,с.
Пример расчета одного из видов трехпараметрической регрессии (экспоненциальной) приведен в листинге 15.13 и на рис. 15.17. В предпоследней строке листинга выведены в виде вектора вычисленные коэффициенты а,ь,с, а в последней строке через эти коэффициенты определена искомая функция f (х).
Регрессия общего вида
15.2.4. Регрессия общего видаВ Mathcad можно осуществить регрессию в виде линейной комбинации C1f1(x)+C2f2 (х) + ..., где fi(х) — любые функции пользователя, a Ci — подлежащие определению коэффициенты. Кроме того, имеется путь проведения регрессии более общего вида, когда комбинацию функций и искомых коэффициентов задает сам пользователь.
Приведем встроенные функции для регрессии общего вида и примеры их использования (листинги 15.14 и 15.15), надеясь, что читатель при необходимости найдет более подробную информацию об этих специальных возможностях в справочной системе и Mathcad Resources.
Регрессия
15.2. РегрессияЗадачи математической регрессии имеют смысл приближения выборки данных (Xi..Yi некоторой функцией f (х), определенным образом минимизирующей совокупность ошибок |f(xi)-yi|. Регрессия сводится к подбору неизвестных коэффициентов, определяющих аналитическую зависимость f(х). В силу производимого действия большинство задач регрессии являются частным случаем более общей проблемы сглаживания данных.
Как правило, регрессия очень эффективна, когда заранее известен (или, по крайней мере, хорошо угадывается) закон распределения данных (xi, yi).
Встроенные функции для сглаживания
15.3.1. Встроенные функции для сглаживанияВ Mathcad имеется несколько встроенных функций, реализующих различные алгоритмы сглаживания данных.
Подробную информацию об алгоритмах, заложенных в функции сглаживания, Вы найдете в справочной системе Mathcad в статье Smoothing (Сглаживание), находящейся в разделе Statistics (Статистика).
Часто бывает полезным совместить сглаживание с последующей интерполяцией или регрессией. Соответствующий пример приведен в листинге 15.16 для функции supsmooth. Результат работы листинга показан на рис. 15.18 (кружки обозначают исходные данные, крестики — сглаженные, пунктирная кривая — результат сплайн-интерполяции). Сглаживание тех же данных при помощи "бегущих медиан" и функции Гаусса с разным значением ширины окна пропускания показаны на рис. 15.19 и 15.20, соответственно.
Скользящее усреднение
15.3.2. Скользящее усреднениеПомимо встроенных в Mathcad, существует несколько популярных алгоритмов сглаживания, на одном из которых хочется остановиться особо. Самый простой и очень эффективный метод — это скользящее усреднение. Его суть состоит в расчете для каждого значения аргумента среднего значения по соседним w данным. Число w называют окном скользящего усреднения; чем оно больше, тем больше данных участвуют в расчете среднего, тем более сглаженная кривая получается. На рис. 15.21 показан результат скользящего усреднения одних и тех же данных (кружки) с разным окном w=3
Устранение тренда
15.3.3. Устранение трендаЕще одна типичная задача возникает, когда интерес исследований заключается не в анализе медленных (или низкочастотных) вариаций сигнала у(х) (для чего применяется сглаживание данных), а в анализе быстрых его изменений Часто бывает, что быстрые (или высокочастотные) вариации накладываются определенным образом на медленные, которые обычно называют трендом. Часто тренд имеет заранее предсказуемый вид, например линейный. Чтобы устранить тренд, можно предложить последовательность действий, реализованную в листинге 15.18.
Полосовая фильтрация
15.3.4. Полосовая фильтрацияВ предыдущих разделах была рассмотрена фильтрация быстрых вариаций сигнала (сглаживание) и его медленных вариаций (снятие тренда). Иногда требуется выделить среднемасштабную составляющую сигнала, уменьшив как более быстрые, так и более медленные его компоненты. Одна из возможностей решения этой задачи связана с применением полосовой фильтрации на основе последовательного скользящего усреднения.
Сглаживание и фильтрация
15.3. Сглаживание и фильтрацияПри анализе данных часто возникает задача их фильтрации, заключающаяся в устранении одной из составляющих зависимости y(xi). Наиболее часто целью фильтрации является подавление быстрых вариаций y(xi), которые чаще всего обусловлены шумом. В результате из быстроосциллирующей зависимости y(xi) получается другая, сглаженная зависимость, в которой доминирует более низкочастотная составляющая.
Наиболее простыми и эффективными рецептами сглаживания (smoothing) можно считать регрессию различного вида (см. разд. 15.2). Однако регрессия часто уничтожает информативную составляющую данных, оставляя лишь наперед заданную пользователем зависимость.
Часто рассматривают противоположную задачу фильтрации — устранение медленно меняющихся вариаций в целях исследования высокочастотной составляющей. В этом случае говорят о задаче устранения тренда. Иногда интерес представляют смешанные задачи выделения среднемасштабных вариаций путем подавления как более быстрых, так и более медленных вариаций. Одна из возможностей решения связана с применением полосовой фильтрации.
Несколько примеров программной реализации различных вариантов фильтрации приведены в данном разделе.
Преобразование Фурье
15.4.1. Преобразование ФурьеМатематический смысл преобразования Фурье состоит в представлении сигнала у(х) в виде бесконечной суммы синусоид вида F(v)sin(vx). Функция F(v) называется преобразованием Фурье или интегралом Фурье, или Фурье-спектром сигнала. Ее аргумент v имеет смысл частоты соответствующей составляющей сигнала. Обратное преобразование Фурье переводит спектр F(V) в исходный сигнал у(х). Согласно определению,
Как видно, преобразование Фурье является существенно комплексной величиной, даже если сигнал действительный.
Вейвлетное преобразование
15.4.2. Вейвлетное преобразованиеВ последнее время возрос интерес к другим интегральным преобразованиям, в частности вейвлетному (или дискретному волновому) преобразованию. Оно применяется, главным образом, для анализа нестационарных сигналов и для многих задач подобного рода оказывается более эффективным, чем преобразование Фурье. Основным отличием вейвлетного преобразования является разложение данных не по синусоидам (как для преобразования Фурье), а по другим функциям, называемым вейвлетобразующими. Вейвле-тобразующие функции, в противоположность бесконечно осциллирующим синусоидам, локализованы в некоторой ограниченной области своего аргумента, а вдали от нее равны нулю или ничтожно малы. Пример такой функции, называемой "мексиканской шляпой", показан на рис. 15.28.
Интегральные преобразования
15.4. Интегральные преобразованияИнтегральные преобразования массива сигнала у(х) ставят в соответствие всей совокупности данных у(х) некоторую функцию другой координаты F(V). Рассмотрим встроенные функции для расчета интегральных преобразований, реализованных в Mathcad.
Адаптивное сглаживание (листинг 15.16)
Адаптивное сглаживание (листинг 15.16)
Двумерная полиномиальная регрессия
Двумерная полиномиальная регрессияПо аналогии с одномерной полиномиальной регрессией и двумерной интерполяцией (см. разд. 15.1.5) Mathcad позволяет приблизить множество точек zi,j(хi, уi) поверхностью, которая определяется многомерной полиномиальной зависимостью. В качестве аргументов встроенных функций для построения полиномиальной регрессии должны стоять в этом случае не векторы, а соответствующие матрицы.
Двумерная полиномиальная регрессия иллюстрируется листингом 15.12 и рис. 15.16. Сравните стиль представления данных для двумерной регрессии с представлением тех же данных для двумерной сплайн-интерполяции (см. листинг 15.6) и ее результаты с исходными данными (см. рис. 15.10) и их сплайн-интерполяцией (см. рис. 15.11).
Двумерная полиномиальная регрессия (листинг 15.12)
Двумерная полиномиальная регрессия (листинг 15.12)
Двумерное преобразование Фурье
Двумерное преобразование ФурьеВ Mathcad имеется возможность применять встроенные функции комплексного преобразования Фурье не только к одномерным, но и к двумерным массивам, т. е. матрицам. Соответствующий пример приведен в листинге 15.21 и на рис. 15.27 в виде графика линий уровня исходных данных и рассчитанного Фурье-спектра.
Экспоненциальная регрессия (листинг 15.13)
Экспоненциальная регрессия (листинг 15.13)
Экстраполяция при помощи функции предсказания (листинг 15.4)
Экстраполяция при помощи функции предсказания (листинг 15.4)
Как видно из рис. 15.9, функция предсказания может быть полезна при экстраполяции данных на небольшие расстояния. Вдали от исходных данных результат часто бывает неудовлетворительным. Кроме того, функция predict хорошо работает в задачах анализа подробных данных с четко прослеживающейся закономерностью (типа рис. 15.8), в основном осциллирующего характера.
Если данных мало, то предсказание может оказаться бесполезным. В листинге 15.5 приведена экстраполяция небольшой выборки данных (из примеров, рассмотренных в предыдущих разделах). Соответствующий результат показан на рис. 15.9 для различных крайних точек массива исходных данных, для которых строится экстраполяция.
Исходное двумерное поле данных (листинг 15.6)
Исходное двумерное поле данных (листинг 15.6)
Исходные данные и обратное преобразование Фурье (листинг 15.20)
Исходные данные и обратное преобразование Фурье (листинг 15.20)
Пример расчета Фурье-спектра для суммы трех синусоидальных сигналов разной амплитуды (показанных в виде сплошной кривой на рис. 15.24), приведен в листинге 15.20. Расчет проводится по N=128 точкам, причем предполагается, что интервал дискретизации данных ух равен А. В предпоследней строке листинга применяется встроенная функция if ft, а в последней корректно определяются соответствующие значения частот Qx. Обратите внимание, что результаты расчета представляются в виде модуля Фурье-спектра (рис. 15.25), поскольку сам спектр является комплексным. Очень полезно сравнить полученные амплитуды и местоположение пиков спектра с определением синусоид в листинге 15.20.
Комплексное преобразование Фурье (продолжение листинга 15.20)
Комплексное преобразование Фурье (продолжение листинга 15.20)
Линейная интерполяция (листинг 15.1)
Линейная интерполяция (листинг 15.1)
Для построения линейной интерполяции служит встроенная функция linterp (листинг 15.1).
Линейная регрессия (листинг 15.7 или 15.8)
Линейная регрессия (листинг 15.7 или 15.8)
Для расчета линейной регрессии в Mathcad имеются два дублирующих друг друга способа. Правила их применения представлены в листингах 15.7 и 15.8. Результат обоих листингов получается одинаковым (рис. 15.12).
Линейная регрессия по методу наименьших квадратов и методу медиан (листинги 15.7 и 15.9)
Линейная регрессия по методу наименьших квадратов и методу медиан (листинги 15.7 и 15.9)
Полиноминальная регрессия
Листинг 15.10. Полиноминальная регрессия
Регрессия отрезками полиномов
Листинг 15.11. Регрессия отрезками полиномов
Регрессия одним полиномом эффективна, когда множество точек выглядит как полином, а регрессия отрезками полиномов оказывается полезной в противоположном случае.
Двумерная полиномиальная регрессия
Листинг 15.12. Двумерная полиномиальная регрессия
Обратите внимание на знаки транспонирования в листинге. Они применены для корректного представления аргументов (например z в качестве вектора, а не строки).
Экспоненциальная регрессия
Листинг 15.13. Экспоненциальная регрессия
Многие задачи регрессии данных различными двухпараметрическими зависимостями у (х) можно свести к более надежной, с вычислительной точки зрения, линейной регрессии. Делается это с помощью соответствующей замены переменных.
Регрессия линейной комбинацией функций пользователи
Листинг 15.14. Регрессия линейной комбинацией функций пользователи
Регрессия общего вида
Листинг 15.15. Регрессия общего вида
Сглаживание с последующей сплайн-интерполяцией
Листинг 15.16. Сглаживание с последующей сплайн-интерполяцией
Сглаживание скользящим усреднением
Листинг 15.17. Сглаживание скользящим усреднением
Приведенная программная реализация скользящего усреднения самая простая, но не самая лучшая Возможно Вы обратили внимание, что все кривые скользящего среднего на рис 15.21 слегка "обгоняют" исходные данные Почему так происходит, понятно согласно алгоритму, заложенному в последнюю строку листинга 15.17, скользящее среднее для каждой точки вычисляется путем усреднения значений предыдущих w точек Чтобы результат скользящего усреднения был более адекватным лучше применить центрированный алгоритм расчета по w/2 предыдущим и w/2 последующим значениям Он будет немного сложнее, поскольку придется учитывать недостаток точек не только в начале (как это сделано в программе с помощью функции условия if) но и в конце массива исходных данных.
Устранение тренда
Листинг 15.18. Устранение тренда
На рис. 15.22 показаны исходные данные (кружками), выделенный с помощью регрессии линейный тренд (сплошной прямой линией) и результат устранения тренда (пунктир, соединяющий крестики).
Полосовая фильтрация
Листинг 15.19. Полосовая фильтрация
Линейная интерполяция
Листинг 15.1. Линейная интерполяция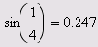
Как видно из листинга, чтобы осуществить линейную интерполяцию, надо выполнить следующие действия:
Быстрое преобразование Фурье
Листинг 15.20. Быстрое преобразование Фурье
Двумерное преобразование Фурье
Листинг 15.21. Двумерное преобразование Фурье

Данные (слева) и их Фурье-спектр (справа) (листинг 15.21)
Поиск вейлет-спектра Даубечи
Листинг 15.22. Поиск вейлет-спектра Даубечи

Вейвлет-спектр на основе функции Даубечи (листинг 15.22)
Поиск вейвлет-спектра на основе "мексиканской шляпы"
Листинг 15.23. Поиск вейвлет-спектра на основе "мексиканской шляпы"
Программа листинга очень проста, но исключительно далека от хорошей в смысле быстродействия. Каждый интеграл вычисляется независимо, без использования методов ускорения, типа применяемых в алгоритме БПФ.
Кубическая сплайн-интерполяция
Листинг 15.2. Кубическая сплайн-интерполяция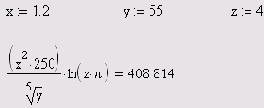
Смысл сплайн-интерполяции заключается в том, что в промежутках между точками осуществляется аппроксимация в виде зависимости A(t) = =а t3+bt2+ct+d. Коэффициенты а, b, с, d рассчитываются независимо для каждого промежутка, исходя из значений уг в соседних точках. Этот процесс скрыт от пользователя, поскольку смысл задачи интерполяции состоит в выдаче значения A(t) в любой точке t (рис. 15.4).
Интерполяция В-сплайнами
Листинг 15.3. Интерполяция В-сплайнами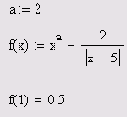
Экстраполяция при помощи функции предсказания
Листинг 15.4. Экстраполяция при помощи функции предсказания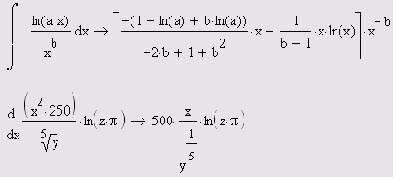
Экстраполяция при помощи функции предсказания
Листинг 15.5. Экстраполяция при помощи функции предсказания
Двумерная интерполяция
Листинг 15.6. Двумерная интерполяция
Линейная регрессия
Листинг 15.7. Линейная регрессия
Другая форма записи линейной регрессии
Листинг 15.8. Другая форма записи линейной регрессии
В Mathcad имеется альтернативный алгоритм, реализующий не минимизацию суммы квадратов ошибок, а медиан-медианную линейную рефессию для расчета коэффициентов а и ь (листинг 15.9).
Построение линейной регрессии двумя разными иетодами (продолжение листинга 15.7)
Листинг 15.9. Построение линейной регрессии двумя разными иетодами (продолжение листинга 15.7)
Различие результатов среднеквадратичной и медиан-медианной рефессии иллюстрируется рис. 15.13.
Обычное построение графика функции от векторной переменной х (листинг 15.1)
Обычное построение графика функции от векторной переменной х (листинг 15.1)
Ошибочное построение графика сплайн-интерполяции (см. листинг 15.2)
Ошибочное построение графика сплайн-интерполяции (см. листинг 15.2)
Чтобы подчеркнуть различия, соответствующие разным вспомогательным функциям cspline, pspline, Ispline, покажем результат действия листинга 15.2 при замене функции cspline в предпоследней строке на линейную ispiine (рис. 15.5). Как видно, выбор вспомогательных функций существенно влияет на поведение A(t) вблизи граничных точек рассматриваемого интервала (0, 6) и особенно разительно меняет результат экстраполяции данных за его пределами.
В заключение остановимся на уже упоминавшейся в предыдущем разделе распространенной ошибке при построении графиков интерполирующей функции (см. рис. 15.3). Если на графике, например являющемся продолжением листинга 15.2, задать построение функции А(Х) вместо A(t), то будет получено просто соединение исходных точек ломаной (рис. 15.6). Так происходит потому, что в промежутках между точками вычисления интерполирующей функции не производятся.
Полиномиальная регрессия
Полиномиальная регрессияПолиномиальная регрессия означает приближение данных (xi, yi) полиномом k-й степени А(х)=а+bх+сх2+dх3+.. .+hxk (рис. 15.14). При k=1 полином является прямой линией, при k=2 — параболой, при k=3 — кубической параболой и т. д. Как правило, на практике применяются k<5.
Для построения регрессии полиномом k-й степени необходимо наличие по крайней мере (k+1) точек данных.
В Mathcad полиномиальная регрессия осуществляется комбинацией встроенной функции regress и полиномиальной интерполяции (см. разд. 15.1.2).
Преобразование Фурье действительных данных
Преобразование Фурье действительных данныхПреобразование Фурье имеет огромное значение для различных математических приложений, и для него разработан очень эффективный алгоритм, называемый БПФ (быстрым преобразованием Фурье). Этот алгоритм реализован в нескольких встроенных функциях Mathcad, различающихся нормировками.
Преобразование Фурье комплексных данных
Преобразование Фурье комплексных данныхАлгоритм быстрого преобразования Фурье для комплексных данных встроен в соответствующие функции, в имя которых входит литера "с".
Преобразование Фурье (листинг 15.20)
Преобразование Фурье (листинг 15.20)
Результат обратного,преобразования Фурье показан в виде кружков на том же рис. 15.24, что и исходные данные. Видно, что в рассматриваемом случае сигнал у(х) восстановлен с большой точностью, что характерно для плавного изменения сигнала.
Программирование других вейвлет-преобразований
Программирование других вейвлет-преобразованийПомимо встроенной функции вейвлет-спектра Даубечи и возможностей пакета расширения Mathcad 11, возможно непосредственное программирование алгоритмов пользователя для расчета вейвлет-спектров. Оно сводится к аккуратному расчету соответствующих семейств интегралов. Один из примеров такой программы приведен в листинге 15.23, а ее результат на рис. 15.30. Анализу подвергается та же функция, составленная из суммы двух синусов, а график двухпараметрического спектра с(а,b) выведен в виде привычных для вейвлет-анализа линий уровня на плоскости (а,b).
Работа функции предсказания в случае малого количества данных (листинг 15.5)
Работа функции предсказания в случае малого количества данных (листинг 15.5)
Разные задачи аппроксимации данных
Разные задачи аппроксимации данных
Как в целях подавления шума, так и для решения других проблем обработки данных, широко применяются различные интегральные преобразования. Они ставят в соответствие всей совокупности данных у(х) некоторую функцию другой координаты (или координат) F(CO). Примерами интегральных преобразований являются преобразование Фурье (см. разд. 15.4.1) и вейвлетное преобразование (см. разд. 15.4.2). Напомним, что некоторые преобразования, например Фурье и Лапласа, можно осуществить в режиме символьных вычислений (см. гл. 5). Каждое из интегральных преобразований эффективно для решения своего круга задач анализа данных.
Для построения интерполяции-экстраполяции в Mathcad имеются несколько встроенных функций, позволяющих "соединить" точки выборки данных (xi, yi) кривой разной степени гладкости. По определению интерполяция означает построение функции д(х), аппроксимирующей зависимость у(х) в промежуточных точках (между xi). Поэтому интерполяцию еще по-другому называют аппроксимацией. В точках xi значения интерполяционной функции должны совпадать с исходными данными, т. е. A(xi) =у(xi).
Везде в этом разделе при рассказе о различных типах интерполяции будем использовать вместо обозначения А(Х) другое имя ее аргумента A(t), чтобы не путать вектор данных х и скалярную переменную t.
Регрессия отрезками полиномов
Регрессия отрезками полиномовПомимо приближения массива данных одним полиномом имеется возможность осуществить регрессию сшивкой отрезков (точнее говоря, участков, т. к. они имеют криволинейную форму) нескольких полиномов. Для этого имеется встроенная функция loess, применение которой аналогично функции regress (листинг 15.11 и рис. 15.15).
Регрессия отрезками полиномов (листинг 15.11)
Регрессия отрезками полиномов (листинг 15.11)
Регрессия полиномами разной степени...
Регрессия полиномами разной степени (коллаж результатов листинга 15.10 для разных k)Пример полиномиальной регрессии квадратичной параболой приведен в листинге 15.10.

Результат двумерной интерполяции (листинг 15.6)
Результат двумерной интерполяции (листинг 15.6)
Результат полосовой фильтрации (листинг 15.19)
Результат полосовой фильтрации (листинг 15.19)
Алгоритм полосовой фильтрации приведен в листинге 15.19, а результат его применения показан на рис. 15.23 сплошной кривой. Алгоритм реализует такую последовательность операций:
Сглаживание при помощи функции ksmooth
Сглаживание при помощи функции ksmooth
Сглаживание "бегущими медианами"
Сглаживание "бегущими медианами"
Скользящее усреднение с разными w=3,5,15 (листинг 15.17, коллаж трех графиков)
Скользящее усреднение с разными w=3,5,15 (листинг 15.17, коллаж трех графиков)
(пунктир), w=5 (штрихованная кривая) и w=is (сплошная кривая) Видно, что при малых w сглаженные кривые практически повторяют ход изменения данных, а при больших w — отражают лишь закономерность их медленных вариаций
Чтобы реализовать в Mathcad скользящее усреднение, достаточно очень простой программы, приведенной в листинге 15.17. Она использует только значения у, оформленные в виде вектора, неявно предполагая, что они соответствуют значениям аргумента х, расположенным через одинаковые промежутки Вектор х применялся лишь для построения графика результата (рис 15.21)
Сплайн-интерполяция (см. листинг 15.2)
Сплайн-интерполяция (см. листинг 15.2)
Сплайн-интерполяция в Mathcad реализована чуть сложнее линейной. Перед применением функции interp необходимо предварительно определить первый из ее аргументов — векторную переменную s. Делается это при помощи одной из трех встроенных функций тех же аргументов (х,у).
Сплайн-интерполяция с выбором коэффициентов линейного сплайна lspline
Сплайн-интерполяция с выбором коэффициентов линейного сплайна lspline
Сравнение синусоиды и вейвлетобразующей функции
Сравнение синусоиды и вейвлетобразующей функции
Из-за своего математического смысла вейвлет-спектр имеет не один аргумент, а два. Помимо частоты, вторым аргументом ь является место локализации вейвлетобразующей функции. Поэтому b имеет ту же размерность, что и х.
Устранение тренда (листинг 15.18)
Устранение тренда (листинг 15.18)
В-сплайн-интерполяция (листинг 15.3)
В-сплайн-интерполяция (листинг 15.3)
Вейвлет-спектр на основе "мексиканской шляпы" (листинг 15.23)
Вейвлет-спектр на основе "мексиканской шляпы" (листинг 15.23)
Встроенная функция вейвлет-преобразования
Встроенная функция вейвлет-преобразованияMathcad имеет одну встроенную функцию для расчета вейвлет-преобразования на основе вейвлетобразующей функции Даубечи.
Математический редактор MathCAD
Числовой ввод-вывод
16.1. Числовой ввод-выводНаиболее простой и распространенный ввод-вывод данных в Mathcad реализован присваиванием и (либо численным, либо символьным) выводом непосредственно в документе. Фактически документ Mathcad является одновременно и кодом программы и результатом ее выполнения. Поэтому самый простой и распространенный способ ввода-вывода — это непосредственное присвоение и вывод вычисленных значений в документах. Числовому вводу и выводу данных посвящена практически вся глава 4 (о вводе данных см. разд. "Типы данных", "Размерные переменные", "Массивы" гл. 4, об управлении формой вывода — разд. "Формат вывода числовых данных" гл 4), поэтому ограничимся напоминанием об этом важном элементе системы Mathcad (листинги 16.1, 16.2).
Лмсттийг 16.1 .Числовой ввод данных
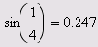
Создание графиков
16.2. Создание графиковВ Mathcad встроено несколько различных типов графиков (см. рисунки этой главы), которые можно разбить на две большие группы.
Все графики создаются совершенно одинаково, с помощью панели инструментов Graph (График), различия обусловлены отображаемыми данными.
Некорректное определение данных приводит, вместо построения графика, к выдаче сообщения об ошибке.
Чтобы создать график, например двумерный Декартов:
Трассировка и увеличение графиков
16.3.10. Трассировка и увеличение графиковТрассировка позволяет очень точно изучить строение графика. Для того чтобы включить режим трассировки, щелкните в области графика правой кнопкой мыши и выберите в контекстном меню пункт Trace (Трассировка). В результате появится окно трассировки (рис. 16.26), а в поле графика Вы увидите две пересекающиеся пунктирные линии.
XY-график двух векторов
16.3.1. XY-график двух векторовСамый простой и наглядный способ получить Декартов график — это сформировать два вектора данных, которые будут отложены вдоль осей х и Y Последовательность построения графика двух векторов х и у показана на рис. 16.3. В этом случае в местозаполнители возле осей вводятся просто имена векторов. Также допускается откладывать по осям элементы векторов, т. е. вводить в местозаполнители возле осей имена хх и yi; соответственно (рис. 16 4). В результате получается график, на котором отложены точки, соответствующие парам элементов векторов, соединенные отрезками прямых линий. Образованная ими ломаная называется рядом данных или кривой (trace).
XY-график вектора и ранжированной переменной
16.3.2. XY-график вектора и ранжированной переменнойВ качестве переменных, откладываемых по любой из осей, можно использовать саму ранжированную переменную (рис. 16.5). При этом по другой оси должно быть отложено либо выражение, явно содержащее саму ранжированную переменную, либо элемент вектора с индексом по этой ранжированной переменной, но никак не сам вектор.
XY-график функции
16.3.3. XY-график функцииНарисовать график любой скалярной функции f (х) можно двумя способами. Первый заключается в дискретизации значений функции, присвоении этих значений вектору и прорисовке графика вектора. Собственно, так и были получены графики синуса на рис. 16.3—165. Второй, более простой способ, называемый быстрым построением графика, заключается во введении функции в один из местозаполнителей (например у оси Y), а имени аргумента — в местозаполнитель у другой оси (рис. 16.6). В результате Mathcad сам создает график функции в пределах значении аргумента, по умолчанию принятых равными от —10 до 10. Разумеется, впоследствии можно поменять диапазон значений аргумента, и график автоматически подстроится под него.
Необходимо заметить, что если переменной аргумента функции было присвоено некоторое значение до построения в документе графика, то вместо быстрого построения графика будет нарисована зависимость функции с учетом этого значения. Примеры двух таких графиков приведены на рис. 16.7.
Полярный график
16.3.4. Полярный графикДля создания полярного графика необходимо нажать кнопку Polar Plot на панели Graph (График) (рис. 16.8) и вставить в местозаполнители имена переменных и функций, которые будут нарисованы в полярной системе координат угол (нижний местозаполнитель) и радиус-вектор (левый местоза-полнитель). Точно так же, как при создании Декартова графика (см. разд. 163.1—16.3.3), по осям могут быть отложены два вектора (рис. 16.8, слева), элементы векторов и ранжированные переменные в различных сочетаниях, а также может быть осуществлено быстрое построение графика функции (рис. 16.8, справа).
Форматирование полярных графиков практически идентично форматированию Декартовых, поэтому все, сказанное ниже об оформлении двумерных графиков на примере XY-графиков, в полной мере относится и к полярным.
Построение нескольких рядов данных
16.3.5. Построение нескольких рядов данныхНа одном графике может быть отложено до 16 различных зависимостей. Чтобы построить на графике еще одну кривую, необходимо выполнить следующие действия:
Чтобы убрать один или несколько рядов данных с графика, удалите клавишами
Описанным способом будет создано несколько зависимостей, относящихся к одному аргументу. На рис. 16.9 построены графики пар точек y(xi) и cos(xi) одного и того же аргумента — элементов вектора хх. Об этом говорит единственная метка х у оси абсцисс. Вместе с тем, имеется возможность отображения на одном и том же графике зависимостей разных аргументов.
Для этого достаточно расставить по очереди метки всех зависимостей у обеих осей.
Форматирование осей
16.3.6. Форматирование осейВозможности форматирования координатных осей графиков включают в себя управление их внешним видом, диапазоном, шкалой, нумерацией и отображением некоторых значений на осях при помощи маркеров.
Форматирование рядов данных
16.3.7. Форматирование рядов данныхС помощью вкладки Traces (Ряды данных) диалогового окна Formatting Currently Selected X-Y Plot (Форматирование выбранного графика) легко установить комбинацию параметров линии и точек для каждого из рядов данных, представленных на графике. Пользователю требуется выделить в списке нужный ряд данных (его положение в списке соответствует положению метки зависимости у оси Y) и изменить в списках в середине диалогового окна желаемые установки (рис. 16.18)
Создание заголовка графика
16.3.8. Создание заголовка графикаЧтобы создать заголовок графика:
Изменение размера и положения графиков
16.3.9. Изменение размера и положения графиковПрежде чем переместить или изменить размер графика, выделите его щелчком мыши. Изменить положение графика в документе можно перетаскиванием, т. е. перемещением указателя при нажатой кнопке мыши. Чтобы изменить размер графика, растягивайте или сжимайте его, перемещая указателем мыши черные прямоугольные маркеры, расположенные на его сторонах.
Двумерные графики
16.3. Двумерные графикиК двумерным графикам относят графики в Декартовой и полярной системах координат. Созданный однажды график одного типа нельзя переделать в график другого типа (в отличие от трехмерных графиков). Для построения XY-графика необходимы два ряда данных, откладываемых по осям х и Y.
Создание трехмерных графиков
16.4.1. Создание трехмерных графиковЧтобы создать трехмерный график, требуется нажать кнопку с изображением любого из типов трехмерных графиков на панели инструментов Graph (График) (если возникнут сложности, обратитесь к. разд. 16.2). В результате появится пустая область графика с тремя осями (рис. 16.30) и единственным местозаполнителем в нижнем левом углу. В этот местозаполнитель следует ввести либо имя z функции z(x,y) двух переменных для быстрого построения трехмерного графика, либо имя матричной переменной z, которая задаст распределение данных zx,y на плоскости XY.
Форматирование трехмерных графиков
16.4.2. Форматирование трехмерных графиковФорматирование трехмерных графиков выполняется с помощью диалогового окна 3-D Plot Format (Форматирование 3-D графика), которое вызывается двойным щелчком мыши в области графика (рис. 16.40). Параметры трехмерных графиков всех типов устанавливаются посредством этого диалогового окна.
Трехмерные графики
16.4. Трехмерные графикиКоллекция трехмерных графиков — настоящее чудо, которое Mathcad дарит пользователю. За считанные секунды Вы можете создать великолепную презентацию результатов своих расчетов.
Создание анимации
16.5. Создание анимацииВо многих случаях самый зрелищный способ представления результатов математических расчетов — это анимация. Mathcad позволяет создавать анимационные ролики и сохранять их в видеофайлах.
Основной принцип анимации в Mathcad — покадровая анимация. Ролик анимации — это просто последовательность кадров, представляющих собой некоторый участок документа, который выделяется пользователем. Расчеты производятся обособленно для каждого кадра, причем формулы и графики, которые в нем содержатся, должны быть функцией от номера кадра. Номер кадра задается системной переменной FRAME, которая может принимать лишь натуральные значения. По умолчанию, если не включен режим подготовки анимации, FRAME=0.
Рассмотрим последовательность действий для создания ролика анимации, например демонстрирующего перемещение гармонической бегущей волны. При этом каждый момент времени будет задаваться переменной FRAME.
Текстовые файлы
16.6.1. Текстовые файлыПеречислим встроенные функции для работы с текстовыми файлами:
Примеры использования встроенных функций иллюстрируются листингами 16.5—16.7. Результат действия листингов 16.5 и 16.7 можно понять, просмотрев получающиеся текстовые файлы, например с помощью Блокнота Windows (рис. 16.60 и 16.61, соответственно).
Графические файлы
16.6.2. Графические файлыПодобно вводу-выводу в текстовые файлы, можно организовать чтение и запись данных в графические файлы различных форматов.
При этом данные отождествляются с интенсивностью того или иного цвета пиксела изображения, находящегося в файле. Перечислим основные функции:
Звуковые файлы
16.6.3. Звуковые файлыВ Mathcad версии 2001 появилась возможность записывать и считывать амплитуду акустических сигналов, записанных в звуковые файлы с расширением .wav:
Ввод-вывод во внешние файлы
16.6. Ввод-вывод во внешние файлыВажный компонент ввода-вывода — это ввод-вывод во внешние файлы. Ввод внешних данных в документы Mathcad применяется чаще вывода, поскольку Mathcad имеет гораздо лучшие возможности представления результатов расчетов, чем многие пользовательские программы. Для общения с внешними файлами данных в Mathcad имеется несколько разных способов. Самый простой из них — использовать имеющееся семейство встроенных функций.
D Bar Plot - график трехмерной гистограммы (рис. 16.35 и 16.36)
3D Bar Plot - график трехмерной гистограммы (рис. 16.35 и 16.36)Для построения графика поверхности необходимо воспользоваться клавишей 3D Bar Plot панели инструментов Graph и следовать указаниям, описанным выше.
D Scatter Plot - график множества...
Быстрое изменение формата графика
Быстрое изменение формата графикаУдобный способ применения некоторых видов форматирования трехмерных графиков заключается в использовании контекстного меню (рис. 16.57). Достаточно нажать на графике правую кнопку мыши и выбрать в контекстном меню одну из опций форматирования. Внешний вид графика сразу изменится.
Быстрое построение графика функции
Быстрое построение графика функции
Быстрое построение графика линий уровня функции (листинг 16.3)
Быстрое построение графика линий уровня функции (листинг 16.3)
Быстрое построение графика множества точек функции (листинг 16.3)
Быстрое построение графика множества точек функции (листинг 16.3)
Быстрое построение графика поверхности функции (листинг 16.3)
Быстрое построение графика поверхности функции (листинг 16.3)
Быстрое построение графика трехмерной гистограммы функции (листинг 16.3)
Быстрое построение графика трехмерной гистограммы функции (листинг 16.3)
Contour Plot - график линий уровня (рис. 16.33 и 16.34)
Contour Plot - график линий уровня (рис. 16.33 и 16.34)Для построения графика поверхности необходимо воспользоваться клавишей Contour Plot панели инструментов Graph и следовать указаниям, описанным выше.
Диалоговое окно 3-D Plot Format
Диалоговое окно 3-D Plot Format
В диалоге 3-D Plot Format (Форматирование 3-D графика) доступно большое количество параметров, изменение которых способно очень сильно повлиять на внешний вид графика. Они сгруппированы по принципу действия на нескольких вкладках. Остановимся коротко на возможностях оформления трехмерных графиков, поясняя их, главным образом, примерами.
Диалоговое окно Axis Format
Диалоговое окно Axis Format
Изменить описанные параметры можно и в диалоговом окне Axis Format (Формат оси), которое появляется, если щелкнуть дважды на самой оси (рис 16 16)
Диалоговое окно Formatting Currently Selected X-Y Plot
Диалоговое окно Formatting Currently Selected X-Y Plot
С помощью флажков и переключателей легко поменять внешний вид каждой из осей Перечислим доступные опции и поясним их действие:
Эффекты перспективы (слева) и тумана (справа)
Эффекты перспективы (слева) и тумана (справа)
Эффект подсветки
Эффект подсветки
Эффект прозрачности в 40% (слева) и 80% (справа)
Эффект прозрачности в 40% (слева) и 80% (справа)
Еще один спецэффект подсветки графика задается на вкладке Lighting (Подсветка) (рис. 16.54), причем имеются как встроенные схемы подсветки (на рис. 16.54 на них наведен указатель мыши), так и возможность задавать ее цвет и направление самому пользователю.
Обратите внимание, что если Вы
Файл, созданный листингами 16.5 и 16.7
Обратите внимание, что если Вы выводите данные в файл, пользуясь встроенной функцией WRITEPRN, то в любом случае создается новый текстовый файл. Если даже до записи данных файл с таким именем существовал, то его содержимое будет уничтожено, заменившись новыми данными. Если Вы хотите сохранить прежнее содержимое текстового файла с данными, пользуйтесь функцией APPENDPRN. Эта встроенная функция может применяться и для создания нового файла. Иными словами, если файла с заданным именем не существовало, то он, после применения, будет создан и наполнен теми данными, которые Вами определены в документе.
созданный листингом
Файл, созданный листингом 16.5
Форматирование графика при помощи контекстного меню
Форматирование графика при помощи контекстного меню
Форматирование осей координат
Форматирование осей координат
Форматирование шкалы
Форматирование шкалыИзменение внешнего вида шкалы, нанесенной на координатную ось, производится с помощью диалогового окна Formatting Currently Selected X-Y Plot (Форматирование выбранного графика), в котором следует перейти на вкладку X-Y Axes (Оси X-Y) (рис. 16.14) Вызвать диалог можно двойным щелчком мыши в области графика или выполнением команды Format / Graph / X-Y Plot (Формат / График / X-Y График), или выбором в контекстном меню команды Format (Формат)
Форматирование скрытых плоскостей графика
Форматирование скрытых плоскостей графика
Форматирование точек данных
Форматирование точек данныхЧтобы построить график в виде только точек данных, перейдите в диалоге форматирования выбранного графика к списку Туре (Тип) и выберите в нем пункт points (точки). Чтобы вместе с точками была показана и кривая, выберите другой тип ряда данных (например линии — lines, см. рис. 16.18).
Форматирование точек данных
Форматирование точек данных
Графики функций от векторного аргумента
Графики функций от векторного аргумента
Графики с отложенными ошибками
Графики с отложенными ошибкамиТип графика с отложенными ошибками довольно сильно отличается от остальных типов, поскольку требует не двух, а трех серий данных. Помимо пар Декартовых (XY) или полярных координат точек необходимо задать еще две последовательности данных, представляющих соответствующие значения ошибок для каждой пары точек (рис. 16.24).
График представления данных с погрешностями требует, чтобы два последовательных ряда данных имели тип графика с ошибками (error).
Графики с заголовками
Графики с заголовками
Графики вектора и ранжированной переменной
Графики вектора и ранжированной переменной
Графики векторного поля, заданные матрицами (листинг 16.4)
Графики векторного поля, заданные матрицами (листинг 16.4)
Приведенные рисунки являются лишь первым шагом в создании красочных графиков. О том, как правильно отформатировать вновь созданные графики, чтобы они приобрели оптимальный с математической точки зрения и эффектный вид, рассказано в следующих разделах.
Улучшить трехмерное представление графика часто позволяет применение к исходным данным интерполяции (см. разд. "Многомерная интерполяция" гл. 15).
График линий уровня, заданный матрицей (листинг 16.4)
График линий уровня, заданный матрицей (листинг 16.4)
График множества точек, заданный...
График множества точек, заданный матрицей (листинг 16.4)График поверхности, заданный матрицей (листинг 16.4)
График поверхности, заданный матрицей (листинг 16.4)
График трехмерной гистограммы, заданный матрицей (листинг 16.4)
График трехмерной гистограммы, заданный матрицей (листинг 16.4)
Изменение диапазона осей
Изменение диапазона осейКогда график создается впервые, Mathcad выбирает представленный диапазон для обеих координатных осей автоматически. Чтобы изменить этот диапазон:
Изменение диапазона оси X
Изменение диапазона оси X
Изменение параметра Rotation (сравните с рис. 16.40)
Изменение параметра Rotation (сравните с рис. 16.40)
Изменение типа графика
Изменение типа графикаЧтобы поменять тип уже имеющегося графика (например построить вместо поверхности график линий уровня и т. д.), просто установите соответствующий переключатель в нижней части вкладки General (Общие) и нажмите кнопку ОК. График будет перерисован.
Кнопка трассировки на панели Graph, кнопка масштабирования — слева от нее
Кнопка трассировки на панели Graph, кнопка масштабирования — слева от нее
Линии различного стиля
Линии различного стиля
Линии разной толщины на полярном графике
Линии разной толщины на полярном графике
Внешний вид точки задает список Symbol (Символ), а их размер — Weight (Толщина). Примеры показаны на рис. 16.21.
Линии сетки на Декартовом и полярном графиках, вид осей — Crossed
Линии сетки на Декартовом и полярном графиках, вид осей — Crossed
Числовой вывод данных (продолжение листинга 16.1)
Листинг 16.2. Числовой вывод данных (продолжение листинга 16.1)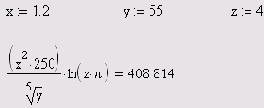
Функция для быстрого построения трехмерных графиков
Листинг 16.3.Функция для быстрого построения трехмерных графиков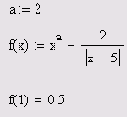
Матрица для отображения на трехмерных графиках
Листинг 16.4. Матрица для отображения на трехмерных графиках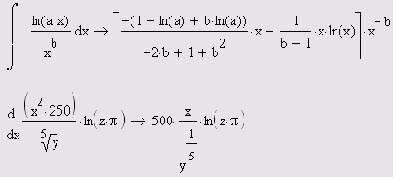
Запись матрицы I в текстовый файл
Листинг 16.5. Запись матрицы I в текстовый файл
Чтение данных из текстового файла в матрицу С
Листинг 16.6. Чтение данных из текстового файла в матрицу С
Дозапись вектора k в соответствующий текстовый файл
Листинг 16.7. Дозапись вектора k в соответствующий текстовый файл
Запись матрицы I в графический файл
Листинг 16.8. Запись матрицы I в графический файл
Чтение из графического...
h2> Файл, созданный листингом 16.8
Маркеры
МаркерыМаркером на координатных осях отмечаются метки некоторых значений Маркер представляет собой линию, перпендикулярную оси, снабженную числом или переменной Чтобы создать маркер
Масштабирование графика
Масштабирование графикаВ поле Zoom (Масштаб) вкладки General (Общие) (см. рис. 16.40) можно задать числовое значение масштаба (рис. 16.45).
Начало создания анимации
Начало создания анимации
Закройте диалог Animate (Анимация) нажатием кнопки Cancel (Отмена) или кнопки управления его окном.Сохраненный видеофайл можно использовать за пределами Mathcad. Скорее всего, если в проводнике Windows дважды щелкнуть на имени этого файла, он будет загружен в проигрыватель видеофайлов Windows, и Вы увидите его на экране компьютера. Таким образом, запуская видеофайлы обычным образом, можно устроить красочную презентацию результатов работы как на своем, так и на другом компьютере.
Настройка заливки графика поверхности
Настройка заливки графика поверхности
Полярные графики
Полярные графики
Построение нескольких зависимостей на одном графике
Построение нескольких зависимостей на одном графике
Построение нескольких зависимостей от разного аргумента
Построение нескольких зависимостей от разного аргумента
Например, чтобы вместо второго (пунктирного) графика на рис. 16.9 построить график не cos(xi), а график параметрической зависимости cos(sin(xi)), достаточно добавить нажатием клавиши с запятой еще одну метку, на этот раз оси х, и ввести в нее выражение sin(x). Результат этих действий показан на рис. 16.10.
При построении на одном и том же графике нескольких зависимостей разного аргумента достаточно позаботиться только о соответствии типа данных для каждой пары точек в отдельности. Например, вполне можно совместно отобразить график функции от ранжированной переменной и график функции, созданный в режиме быстрого построения (рис. 16.11).

Построение зависимостей от разного аргумента разного типа данных
Просмотр графика в увеличенном масштабе
Просмотр графика в увеличенном масштабе
Просмотр созданного ролика анимации
Просмотр созданного ролика анимации
При создании файлов анимации допускается выбирать программу видеосжатия (кодек) и качество компрессии. Делается это с помощью кнопки Options (Опции) в диалоговом окне Animate (Анимация).
Расположение координатных осей по периметру
Расположение координатных осей по периметру
Различные типы рядов данных
Различные типы рядов данных
Различный стиль и размер точек данных
Различный стиль и размер точек данных
Редактирование точек данных
Редактирование точек данныхНа многих типах графиков допускается показ точек данных. Формат точек, включая тип символа, размер, соединение их линией задается на вкладке Appearance (Оформление) (рис. 16.56). Опции форматирования точек те же самые, что и для двумерных графиков (см. разд. 16.3.7).
Результат изменения диапазона осей
Результат изменения диапазона осей
Чтобы вернуть автоматический выбор какого-либо диапазона, удалите число из соответствующего поля и щелкните вне его. Граница шкалы будет выбрана Mathcad, исходя из значений данных, представляемых на графике.
Сохранение установок по умолчанию
Сохранение установок по умолчаниюНа вкладке Defaults (По умолчанию) диалога Formatting Currently Selected X-Y Plot (Форматирование выбранного графика) находятся два элемента управления:
Создание Декартового графика при помощи панели Graph
Создание Декартового графика при помощи панели Graph
Если имена данных введены правильно, нужный график появится на экране. Созданный график можно изменить, в том числе меняя сами данные, форматируя его внешний вид или добавляя дополнительные элементы оформления.
Правильному заданию данных и форматированию графиков посвящены соответствующие разделы этой главы.
Самый наглядный способ создания графика — с помощью панели инструментов Graph (График). Однако точно так же создаются графики путем выбора соответствующего элемента подменю Insert / Graph (Вставка / График), показанного на рис. 16.2, либо нажатием соответствующей типу графика горячей клавиши.
Чтобы удалить график, щелкните в его пределах и выберите в верхнем меню Edit (Правка) пункт Cut (Вырезать) или Delete (Удалить).
Создание графика посредством меню
Создание графика посредством меню
Создание графика с отложенными ошибками
Создание графика с отложенными ошибками
На рис. 16.24 отложено три ряда данных: у (сами данные), erroru (верхняя метка ошибок), errorU (нижняя метка ошибок). Для двух последних рядов выставлен тип error (ошибки).
Создание маркеров (слева) и готовые маркеры (справа)
Создание маркеров (слева) и готовые маркеры (справа)
При создании маркеров очень полезной бывает трассировка графиков, позволяющая точно определить значение маркера (см разд 16 3 10)
Создание трехмерного графика
Создание трехмерного графика
Рассмотрим на простом примере функции z(x,y) и матрицы z (они заданы в листингах 16.3 и 16.4, соответственно) примеры построения трехмерных графиков различных типов, создаваемых нажатием той или иной кнопки на панели Graph (График). Еще раз отметим, что для получения графиков не требуется никакого текста, кроме введения имени соответствующей функции или матрицы в местозаполнитель.
Для графиков, задаваемых матрицами, шкалу плоскости XY приходится задавать вручную. Mathcad просто рисует поверхность, точки в пространстве или линии уровня, основываясь на двумерной структуре этой матрицы. При быстром же построении графиков имеется возможность строить их в различном диапазоне аргументов, подобно двумерным графикам.
Спецэффекты
СпецэффектыВ той же вкладке Advanced (Дополнительно) (рис. 16.50) имеется доступ к управлению несколькими специальными эффектами оформления графиков, благодаря которым они смотрятся более красиво.
Перечислим эти эффекты:
Стиль осей
Стиль осейС помощью группы переключателей Axes Style (Стиль осей) можно задать один из следующих стилей осей координат:
Стиль, толщина и цвет линии
Стиль, толщина и цвет линииИзменяя параметры линии, можно добиться наилучшего восприятия разных зависимостей на одном графике (рис. 16.19—16.20).
Стиль заливки и линий
Стиль заливки и линийНа рис. 16.48 и 16.49 показано влияние различного стиля задания заливки и линий с помощью вкладки Appearance (Появление) для контурного и поверхностного графиков. При выборе переключателя Fill Surface (Заливка поверхности) из группы Fill Options (Опции заливки) (рис. 16.48) Вы получаете доступ к опциям цвета (в группе Color Options). Если выбрать переключатель Solid Color (Один цвет), то получится однотонная заливка поверхности, показанная на рис. 16.49. Если установить переключатель Colormap (Цветовая схема), то поверхность или контурный график будут залиты разными цветами и оттенками (рис. 16.48), причем выбрать цветовую схему можно на вкладке Advanced (Дополнительно) (рис. 16.50).
Столбчатые графики (гистограммы)
Столбчатые графики (гистограммы)В Mathcad есть несколько столбчатых типов графиков, подходящих для построения гистограмм (об их практическом применении читайте в гл. 13). Три различных типа иллюстрируются рис. 16.23.
Столбчатые типы графиков
Столбчатые типы графиков
Surface Plot - график поверхности (рис. 16.31 и 16.32)
Surface Plot - график поверхности (рис. 16.31 и 16.32)Для построения графика поверхности необходимо воспользоваться клавишей Surface Plot панели инструментов Graph и следовать указаниям, описанным выше.
Типы рядов данных
Типы рядов данныхНесколько различных типов рядов данных представлено на рис. 16.22.
Для полярных графиков также допускается устанавливать любые из перечисленных типов (пример см ниже на рис. 16.25).
Трассировка графика
Трассировка графика
Перемещая указатель мыши по графику, Вы тем самым передвигаете точку пересечения линий трассировки При этом координаты точки указываются с высокой точностью в окне трассировки в полях X-Value (Значение X) и Y-Value (Значение Y). Нажатие кнопки Сору X (Копировать X) или Copy Y (Копировать Y) копирует соответствующее число в буфер обмена. В дальнейшем его можно вставить в любое место документа или в маркер, нажав клавиши
Если установлен флажок Track Data Points (Следовать за рядом данных), как это показано на рис. 16.26, то линии трассировки следуют точно вдоль графика. Если нет, то они могут перемещаться по всей области графика.
Помимо трассировки, в Mathcad предусмотрена еще одна удобная возможность просмотра графика в увеличенном масштабе. Для вызова диалогового окна Zoom (Масштаб графика) выберите в контекстном меню, либо в меню Format (Формат) пункты Graph (График) и Zoom (Масштаб). После этого указателем мыши выберите прямоугольную область на графике, которую Вы планируете просмотреть в увеличенном масштабе (рис. 16.27), и нажмите кнопку Zoom (Увеличить). В результате часть графика будет прорисована более крупно (рис. 16.28). Далее можно либо продолжать изменять масштаб, либо вернуться к прежнему виду графика кнопкой Full View (Показать целиком), либо закрыть диалог Zoom для окончательной перерисовки графика в крупном масштабе (нажав кнопку ОК)
Возможно, Вам покажется более удобным вызов окон трассировки и масштабирования графиков с помощью панели инструментов Graph (График) (рис. 16.29). Эти кнопки доступны только при выделенном двумерном графике
Управление масштабом графика
Управление масштабом графика
Установлен флажок Show Box
Установлен флажок Show Box
Vector Field Plot - график векторного поля (рис. 16.39)
Vector Field Plot - график векторного поля (рис. 16.39)График векторного поля несколько отличается от остальных типов двумерных графиков. Его смысл заключается в построении некоторого вектора в каждой точке плоскости XY. Чтобы задать вектор на плоскости, требуются два скалярных числа. Поэтому в Mathcad принято, что векторное поле задает комплексная матрица. Действительные части каждого ее элемента задают проекцию вектора на ось х, а мнимые — на ось у.
Вид того же графика
Вид того же графика (рис. 16.41) при углах Rotation=0, Tilt=20 и Twist=200
Вкладка Special
Вкладка Special
Вкладка Traces диалога Formatting Currently Selected X-Y Plot
Вкладка Traces диалога Formatting Currently Selected X-Y Plot
На вкладке Traces (Ряды данных) регулируются следующие параметры:
Вращение графика
Вращение графикаСамый простой способ ориентации системы координат с графиком в трехмерном пространстве — это перетаскивание ее указателем мыши. Попробуйте перемещать при нажатой левой кнопке мыши указатель в пределах графика, и Вы увидите, как поворачивается график.
Разумеется, поворачивать можно лишь графики в трехмерном пространстве; векторное поле и линии уровня строятся, по определению, на прямоугольном участке плоскости.
Другой способ изменения ориентации графика — с помощью полей Rotation (Вращение), Tilt (Наклон) и Twist (Поворот) на вкладке General (Общие) (см. рис. 16.40), которые в совокупности определяют соответствующие углы (в градусах) и тем самым задают направление всех трех осей координат в пространстве. Сравнивая рис. 16.40—16.42, Вы разберетесь, как эти углы влияют на ориентацию графика.
Выбор цветовой схемы
Выбор цветовой схемы
XY-график двух векторов
XY-график двух векторов
XY-график двух векторов, заданных элементами
XY-график двух векторов, заданных элементами
Обратите внимание, что Mathcad автоматически определяет границы графика, исходя из диапазона значений элементов векторов
Стоит отметить, что подобным образом легко создать и XY-график столбцов или строк матрицы, применяя оператор выделения столбца и откладывая соответствующие выражения по осям графика (множество подобных примеров Вы найдете на рисунках гл. 11 и 12).
Заголовок графика
Заголовок графикаЗаголовок графика определяется на вкладке Title (Заголовок) и может быть расположен как сверху, так и снизу графика (рис. 16.55).
Заголовок сверху и снизу графика
Заголовок сверху и снизу графика
Заливка поверхности белым цветом (слева) и серым цветом (справа)
Заливка поверхности белым цветом (слева) и серым цветом (справа)
Поэкспериментируйте с разными цветовыми схемами и представлениями заливки и линий, задаваемых полем One Options (Опции линии) (рис. 16.48), чтобы представлять себе богатство возможностей Mathcad. Некоторые параметры, влияющие на представление контуров графиков, доступны на вкладке Special (Специальные) (рис. 16.51). Сочетаний различных цветовых схем, заливок и других параметров настолько много, что лучше предоставить читателю самому попробовать применить их различные комбинации и выбрать из них наиболее понравившиеся.
Математический редактор MathCAD
Элементы оформления
17.1.1. Элементы оформленияПеречислим элементы оформления документов, которые допускается применять в Mathcad как, собственно, для проведения математических расчетов, так и в чисто декоративных целях (рис. 17.1, сверху вниз):
Размещение элементов оформления в документах
17.1.2. Размещение элементов оформления в документахВажной составляющей оформления расчетов является правильное и понятное размещение объектов по документу Mathcad.
Работа с зонами
17.1.4. Работа с зонамиУчастки документа Mathcad можно объединять в зоны (area). Часто их в русском переводе называют областями, что создает путаницу с термином область, который в данной книге эквивалентен понятию регион (region). Например, в этой и других главах мы говорим о текстовой или математической области. Собственно говоря, зоны включают в себя различные области.
Зоны могут понадобиться для следующих целей:
Элементы оформления документов
17.1. Элементы оформления документовРасчеты в Mathcad могут быть оформлены по-разному:
Форматирование текста
17.2.1. Форматирование текстаФорматирование текста заключается в управлении его двумя основными составляющими:
Стили текста и формул
17.2.2. Стили текста и формулКогда Вы начинаете вводить текст в текстовый регион или формулы в математический регион, формат шрифта и абзаца выбирается в соответствии со стилями, выбранными по умолчанию и сохраненными в шаблоне документа.
Текстовый стиль содержит информацию обо всех установках шрифта и абзаца текстового региона, а математический стиль — об установках только шрифта различных элементов формул (но не абзаца, т. к. каждая формула по умолчанию не может занимать более одной строки).
Форматирование текста и формул
17.2. Форматирование текста и формулДля форматирования текста и формул служит панель инструментов Formatting (Форматирование). С ее помощью текстовые области можно форматировать двумя способами.
Параметры страницы
17.3.1. Параметры страницыРасположение документа на странице при распечатке его на принтере задается в диалоговом окне Page Setup (Параметры страницы) (рис. 17.22), которое вызывается одноименной командой меню File (Файл) В этом диалоговом окне определяются следующие параметры
Колонтулы
17.3.2. КолонтулыКолонтитулами называют элементы оформления документа, которые появляются в унифицированном виде на каждой странице печатной копии документа Чтобы вставить колонтитулы в документ:
Установки документа
17.3.3. Установки документаОсновные элементы оформления документа сохраняются в его установках (settings). Они автоматически сохраняются вместе с содержимым в Mathcad-файле и могут быть использованы в качестве установок по умолчанию при создании нового документа на основе шаблона (см. разд. "Создание документа на основе шаблона"гл. 2).
Перечислим установки документа:
Оформление страниц
17.3. Оформление страницMathcad имеет некоторый набор средств для оформления страниц в целом, которые можно разделить на управление параметрами разметки страницы и на создание верхних и нижних колонтитулов.
Установка тега
17.4.1. Установка тегаПрежде чем определить гиперссылку, можно сначала точно определить место в документе, на которое эта гиперссылка будет переводить курсор и которое в Mathcad называется тегом (tag). Для установки тега:
Вставка гиперссылки
17.4.2. Вставка гиперссылкиСоздавать гиперссылку можно в любом месте любого документа. Щелчок на гиперссылке будет переводить курсор на место тега, на который установлена гиперссылка, либо (при отсутствии тега) в начало документа, на который произведена гиперссылка. Для вставки гиперссылки:
Ссылки
17.4.3. СсылкиПомимо гиперссылок, иногда стоит применять другие схожие с ними объекты, называемые ссылками (reference). Ссылка на документ А, вставленная в некоторое место документа В, приводит к расчету всего документа А внутри документа В. Таким образом, ссылки позволяют хранить вложенные друг в друга расчеты в разных файлах.
Ссылки могут понадобиться, если группа разработчиков решает одну большую задачу. В этом случае после распределения задач и соглашения об именах глобальных и локальных переменных каждый разработчик создает свой файл с расчетами
Для установки ссылки достаточно выбрать команду Insert / Reference (Вставка / Ссылка) и затем в диалоговом окне Insert Reference (Вставка ссылки) определить путь к имени файла-ссылки. В примере, показанном на рис. 17.27, в файле отсутствует описание функции f(x), зато оно есть в файле, на который оформляется ссылка. Поэтому после нажатия кнопки ОК на месте курсора ввода появится информация о файле-ссылке, а результат функции f (1) будет рассчитан в соответствии с формулами этого файла.
 |
 |
 |
Ссылки и гиперссылки
17.4. Ссылки и гиперссылкиГиперссылки — это активные области в документах Mathcad, которые выводят на экран какое-либо другое место в активном документе, другой документ Mathcad или другого приложения, либо на сайт в Интернете. Гиперссылки эффективны в больших документах, а также в обучающих и презентационных системах, выполненных в Mathcad. Особенно важно уметь пользоваться гиперссылками, если Вы разрабатываете электронные книги.
Рисунки
17.5. РисункиMathcad 11 имеет средства оформления документов, позволяющие вставлять и редактировать рисунки, сохраненные в файлах самых разных графических форматов. Эти средства придают Mathcad 11 основные функции графического редактора.
Абзац
АбзацДля установки параметров абзаца применяются:
Дополнительная и реже применяемая возможность форматирования текста — установка. Инструкции по установке знаков табуляции Вы найдете в справочной системе Mathcad.
Блокирование зоны
Блокирование зоны
Чтобы открыть или разблокировать зону, выберите в главном меню пункт Format / Area / Unlock (Формат / Область / Открыть). Если зона была заперта с защитой паролем, то этот пароль будет запрошен при разблокировании зоны (рис. 17.11). Запертая зона отображается со значками в форме замков в левом углу горизонтальных линий, ее обрамляющих.
На рис. 17.11 вы видите запертую зону с информацией о времени ее блокирования, поскольку в диалоге Lock Area (Запереть область) был установлен флажок Show lock timestamp (Показать время блокировки). Если в диалоге Lock Area установить другой флажок — Collapse when locked (Скрыть при блокировке), то запертая зона будет скрыта с экрана.
Диалоговое окно Paragraph Format
Диалоговое окно Paragraph Format
Диалоговое окно Text Format
Диалоговое окно Text Format
Форматирование формул
Форматирование формулДля математических регионов можно применять все рассмотренные способы форматирования шрифта при помощи панели Formatting (Форматирование). Особенность форматирования формул заключается в том, что изменения шрифта, примененные к отдельному параметру в одной формуле, немедленно приводят к его изменению во всех формулах в документе (там, где этот параметр присутствует) (рис. 17.17, 17.18). При этом следует знать, что формулы содержат элементы, выполненные в нескольких математических стилях. К примеру, на рис. 17.17 изменяется шрифт составляющих всех формул документа, выполненных в стиле Variables (Переменные), а на рис. 17.18 — шрифт элементов формул в стиле Constants (Константы). О принадлежности редактируемой части формулы к тому или иному стилю можно судить по имени стиля, отображаемому в левом углу панели Formatting (Форматирование).
Изменение размера областей
Изменение размера областейРассматривая рис. 17.2, можно заметить, что по сторонам всех областей, за исключением математических, при выделении располагаются черные прямоугольники, называемые маркерами или ручками (handle). С их помощью осуществляется растягивание или сжатие областей в соответствующих направлениях. Если поместить указатель мыши на ручку, то он приобретет форму двойной стрелки, перетаскивая которую можно изменить размер области.
Размер формул изменить таким образом нельзя. Для форматирования (в том числе, управления размером и типом шрифта) как формул, так и текста в текстовых областях, следует пользоваться панелью Formatting (Форматирование) (см. разд. 17.2).
Помните о том, что изменение масштаба представления документа в меню View / Zoom (Вид / Масштаб) влияет только на его экранное представление внутри Mathcad, но не сохраняется в файле и не влияет на распечатку на принтере.
Изменение шрифта элементов формулы, выполненных в стиле констант
Изменение шрифта элементов формулы, выполненных в стиле констант
Изменение шрифта элементов формулы, выполненных в стиле переменных
Изменение шрифта элементов формулы, выполненных в стиле переменных
Изменение стиля
Изменение стиляДля того чтобы изменить установки текстового или математического стиля или создать новый стиль пользователя, выберите в меню Format пункт Style (Стиль) или Equation (Формула). Рассмотрим изменение текстового стиля (рис. 17.19). В диалоговом окне Text Style (Стиль текста) нажмите кнопку Modify (Изменить) и в появившемся новом диалоговом окне Define Style (Определение стиля) отредактируйте параметры шрифта и абзаца, которые будут присущи данному стилю. Текущее описание стиля можно наблюдать в нижней части диалога Define Style (Определение стиля) в рамке Description (Описание).
Изменение стиля переменной
Изменение стиля переменной
Изменение текстового стиля
Изменение текстового стиля
Области с обрамлением (слева) и без обрамления (справа)
Области с обрамлением (слева) и без обрамления (справа)
Основные элементы оформления документов Mathcad
Основные элементы оформления документов Mathcad
За пределами границ областей находится пустая часть документа. Кроме перечисленных, часто бывает полезным применение следующих дополнительных элементов оформления:
Параметры страницы
Параметры страницы
При изменении какого-либо параметра его влияние можно оценить в области предварительного просмотра в верхней части диалогового окна, в которой изображается макет печатной копии страницы Кроме того, установка полей в диалоговом окне Page Setup (Параметры страницы) влияет на положение линий раздела границ, которые Вы видите на рабочей области документа Mathcad.
Перемещение областей по документу
Перемещение областей по документуЧтобы изменить место расположения любой области в документе Mathcad:
Помещение формул внутрь зоны
Помещение формул внутрь зоны
Изменить размеры зоны можно в любой момент, щелкнув на любой из горизонтальных линий (в результате чего она будет выделена) и передвинув ее в новое положение. Для удаления зоны из документа выделите щелчком мыши любую из горизонтальных линий и нажмите клавишу
Чтобы поместить формулу внутрь зоны, просто перетащите ее туда указателем мыши (рис. 17.8).
Правка гиперссылки
Правка гиперссылки
Применение стиля к формуле
Применение стиля к формулеИногда требуется применить стиль шрифта к одной из переменных или чисел, чтобы она отличалась от остальных. Для этого измените математический стиль переменной Выполните следующие действия (рис. 17.20):
Одноименные переменные, записанные в разном стиле, являются разными переменными! Если Вы желаете поменять математический стиль переменной, меняйте его везде, где переменная встречается в документе Соответствующий пример приведен на рис 17 21, на котором переменная х в разных стилях по-разному идентифицируется Mathcad
Если стиль не нужно изменять, применить его к формуле можно более просто, выбрав из списка стилей на панели форматирования.
Применение стиля к формуле или тексту
Применение стиля к формуле или текстуИзменить форматирование формулы или абзаца текстового региона целиком можно с помощью применения к нему стиля. Для этого выделите абзац или формулу, а затем выберите из списка стилей стиль, который Вы желаете применить к формуле или абзацу текста (см. рис. 17.12).
Примеры оформления абзаца
Примеры оформления абзаца
Примеры шрифтового оформления текста
Примеры шрифтового оформления текста
Разблокирование зоны
Разблокирование зоны
Разделение областей
Разделение областейЧасто при работе с Mathcad, по мере перетаскивания областей с места на место, оказывается, что одни из них перекрываются другими и перестают быть видны на экране. Чтобы разделить области, примените удобную возможность, предусмотренную разработчиками Mathcad.
Если Вы по какой-либо причине считаете, что некоторые регионы должны в документе перекрываться, то порядком их наложения друг на друга можно управлять при помощи команд контекстного меню Bring to Front (На передний план) или Send to Back (На задний план).
Разделение областей
Разделение областей
Редактор Mathcad, в силу математической специфики, отличается от большинства текстовых процессоров, с которыми, как правило, пользователи не испытывают трудностей Встретив сложности при работе с редактором, что не является редкостью, обратитесь к первой части книги (см гп 2).
Редактирование рисунка при помощи панели Picture
Редактирование рисунка при помощи панели Picture
Шрифт
ШрифтШрифт выделенного текста можно поменять при помощи панели Formatting (Форматирование) (рис. 17.13), либо при помощи диалогового окна Text Format (Формат текста) (рис. 17.14). Чтобы вызвать это диалоговое окно, следует выбрать пункт Text (Текст) в верхнем меню Format (Формат) или пункт Font (Шрифт) в контекстном меню. Перечислим параметры шрифта и соответствующие элементы этой панели, которыми допускается управлять:
Скрытие зоны
Скрытие зоныЧтобы скрыть зону, дважды щелкните мышью на любой из линий, ее выделяющих. Альтернативный способ заключается в помещении курсора внутрь зоны и выполнении команды Format / Area / Collapse (Формат / Область / Скрыть). Сразу после этого содержимое зоны будет убрано с экрана, но по-прежнему будет участвовать в расчетах (рис. 17 9)
Вернуть зону на экран можно точно так же: двойным щелчком на линии, показывающей наличие скрытой зоны (рис. 17.9), либо выбором команды Format / Area / Expand (Формат / Область / Раскрыть).
Применение скрытых зон эффективно в документах большого размера
Скрытие зоны
Скрытие зоны
Создание ссылки
Создание ссылки
Для вставки рисунка в документ:
Создание зоны
Создание зоныЧтобы создать новую зону в документе, достаточно поместить курсор ввода в желаемое место и выбрать в верхнем меню пункт Insert / Area (Вставить / Область). В результате, в выбранном месте документа появится пара горизонтальных линий, отмеченных у левого края значком в виде черного треугольника (рис. 17.7). Часть документа, оказавшаяся между этими линиями, и образует зону.
Создание зоны
Создание зоны
Список стилей форматирования текста
Список стилей форматирования текста
Форматирование текста (и, отчасти, формул) в Mathcad во многом похоже на форматирование в большинстве текстовых редакторов, поэтому остановимся коротко на возможностях шрифтового оформления и редактировании параметров абзацев и страниц. Разберем сначала второй способ, относящийся к форматированию текста, чтобы ясно представлять соответствующие возможности Mathcad.
Стиль влияет на идентификацию переменной Mathcad
Стиль влияет на идентификацию переменной Mathcad
Удаление области
Удаление областиУниверсальный метод удаления области целиком — выбор в главном меню пункта Edit / Delete (Правка / Удалить). Различные области можно также удалить многократным нажатием клавиш
Установка колонтитулов
Установка колонтитулов
Установка тега
Установка тега
Если Вы все сделали правильно, то при двойном щелчке на гиперссылке будет осуществлен переход на место, где расположен тег, т. е. в нашем примере на документ 17.25.mcd. Чтобы отредактировать гиперссылку, достаточно, находясь на ее области, выбрать тот же пункт меню Insert / Hyperlink (Вставка / Гиперссылка). Появится диалог Edit Hyperlink (Правка гиперссылки), в котором можно исправить ее параметры (см. рис. 17.26). Удалить гиперссылку можно нажатием кнопки Remove Link (Удалить гиперссылку).
Помимо гиперссылок на документы Mathcad, допускается создавать гиперссылки на другие файлы (например видеофайлы или HTML-файлы), в том числе, находящиеся в Интернете. Для этого достаточно указать соответствующий адрес URL в верхнем текстовом поле диалога Edit Hyperlink (Вставка гиперссылки).
Внешний вид колонтитулов в режиме предварительного просмотра страницы
Внешний вид колонтитулов в режиме предварительного просмотра страницы
Перечислим кнопки, которые осуществляют автоматическую вставку информации в колонтитул. В фигурных скобках отображен символ, который определяет соответствующую информацию в поле колонтитула.
Вставка новой области
Вставка новой областиДля вставки того или иного элемента нужно предварительно выбрать место в документе, куда он будет вставлен. Это осуществляется с помощью курсора ввода (крестика, показанного на рис. 17.1 в правом нижнем углу, на который наведен указатель мыши). Затем следует воспользоваться соответствующим пунктом меню Insert (Вставка), либо одной из панелей инструментов, либо, как для ввода формулы, просто начать вводить символы с клавиатуры.
Приемы вставки различных областей были рассмотрены выше в соответствующих разделах книги (например, формулы — в гл 2, графики — в гл 15 и т.д).
Помните, что компоненты вставляются при помощи пункта меню Insert / Component (Вставка / Компонент), а внедренный объект можно вставить, поместив его в буфер обмена из области другого приложения и, после переключения в Mathcad, нажав сочетание клавиш
Вставка области с рисунком
Вставка области с рисунком
Если ввести в местозаполнитель имя какой-либо определенной ранее в документе матрицы, то созданный рисунок отразит строение этой матрицы Данная опция очень эффективна для визуализации матриц большого размера, особенно разреженных
Как только пользователь выделит рисунок, щелкнув на нем мышью, на экран автоматически будет вызвана панель инструментов Picture (Рисунок) (рис 17.29). Она позволяет редактировать рисунок, применяя довольно развитые графические средства, например, отражение рисунка, увеличение его фрагмента и т. п. Назначение большинства кнопок на панели Picture (Рисунок) совпадает с наиболее известными графическими редакторами Вставка областей с рисунками позволяет оформить документы более эффектно
Вычисление формулы в центре выключено
Вычисление формулы в центре выключено
Выделение области цветом
Выделение области цветомЧтобы выделить область цветом, вызовите нажатием на ней правой кнопкой мыши контекстное меню и выберите в нем пункт Properties (Свойства), либо выберите такой же пункт в меню Format (Формат). Установите в диалоговом окне Properties (Свойства) флажок Highlight Region (Выделить цветом) и нажмите кнопку ОК (рис. 17.4) Область будет выделена цветом, по умолчанию желтым (текст, показанный в левой верхней части рис. 17.4, выделен серым)
После установки флажка Highlight Region (Выделить цветом) становится доступной кнопка Choose Color (Выбрать цвет), с помощью которой можно выбрать любой другой цвет выделения из палитры. Именно так была выделена формула на рис. 17.4.
Выделение области цветом
Выделение области цветом
Многие формулы из Mathcad Resources выделены цветом. После того как Вы скопировали какие-либо формулы в документ, выделение можно убрать снятием флажка проверки в диалоговом окне Properties (Свойства).
Для того чтобы задать цвет фона всего документа, выберите команду Format / Color / Background (Формат / Цвет / Фон) и определите в палитре понравившийся Вам цвет.
Выделение области обрамлением
Выделение области обрамлениемВыделить область можно не только цветом, но и обрамлением (рис. 17.5). Для включения обрамления установите флажок Show Border (Показать рамку) в том же самом диалоговом окне Properties (Свойства). Обрамление может применяться вместе с выделением цветом (так выделена текстовая область на рис. 17.5).
Напомним, что при помощи закладки Calculations (Вычисления) того же самого диалога Properties (Свойства) можно выключить отдельные формулы из процесса вычислений (см. гл. 3). Такие формулы отображаются в документе с прямоугольной точкой в углу (рис. 17.6).
Выделение основных элементов оформления (коллаж)
Выделение основных элементов оформления (коллаж)
Чтобы создать копию области в другом месте документа, начните перетаскивать ее обычным образом, а затем нажмите и удерживайте, вплоть до отпускания клавиши мыши там, где хотите поместить область, клавишу
Запирание зоны
Запирание зоныЗоны можно не только скрывать и раскрывать, но и запирать или блокировать, т. е. закрывать для любого редактирования. Для запирания зоны выберите команду Format / Area / Lock (Формат / Область / Запереть). В появившемся диалоговом окне (рис. 17.10) следует нажать кнопку ОК. Для того чтобы запретить несанкционированный доступ к редактированию зоны другим пользователям, предварительно введите пароль (Password) в верхнем текстовом поле, повторите ввод пароля в нижнем текстовом поле, дабы избежать возможных ошибок, и затем нажмите кнопку ОК.
Математический редактор MathCAD
Управление документами
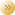 Биржевой анализ: Технический анализ - Инструменты - Софт
Биржевой анализ: Технический анализ - Инструменты - Софт
- Биржевой анализ - Технический анализ
- Обучение техническому анализу
- Индексы технического анализа
- Индикаторы технического анализа
- Методы технического анализа
- Графика в техническом анализе
- Технический анализ рынков
- Российский технический анализ
- Инструменты технического анализа
- Математика в биржевом анализе
- Разновидности биржевого анализа
- Mathematica в биржевом анализе
- MathCAD в биржевом анализе
- Maple в биржевом анализе
- Matlab в биржевом анализе