
|
Нелинейный портфельный анализ и распределение ресурсов - А. А. Новоселов
Красноярский государственный университет Кафедра ценных бумаг и страхового дела
Аннотация
В работе рассматривается проблема распределения ограниченных ресурсов в условиях вероятностной неопределенности (риска). Приведен пример, в котором классические теории второго порядка оказываются неработоспособными. Представлены современные методы портфельного анализа, справляющиеся с проблемой.
Введение
Задачу портфельного анализа (или распределения ограниченных ресурсов) можно неформально представить следующим образом: имеется несколько направлений инвестирования (инвестиционных инструментов), каждое из которых может принести не вполне определенный результат (доход); требуется распределить ресурсы (капитал) таким образом, чтобы достигнуть наилучшего в некотором смысле результата. Близкой по духу является и задача принятия решений, когда нужно выбрать один из нескольких проектов, каждый из которых также приносит не вполне определенный заранее доход. Поскольку неопределенность результата обычно моделируется теоретиковероятностными методами, задача сводится к сравнению вероятностных распределений.В классическом портфельном анализе сравнение распределений производится на основании только двух моментов распределения: математического ожидания и дисперсии; или, в многомерном случае, вектора средних значений и ковариационной матрицы. Этот подход, который естественно назвать теорией второго порядка (по количеству используемых моментов распределения), восходит к работам Марковица, Тобина, и для статического случая получает логическое завершение в модели эффективного рынка CAPM Шарпа. Динамический вариант подхода был применен в работах Блэка, Шоулза и Мертона для вычисления цены опционов. Теорию второго порядка можно также называть линейной теорией по структуре методов решения получаемых задач.
Линейная теория хорошо работает в случае нормального совместного распределения инструментов; фактически предположение о нормальности распределений явно или неявно присутствует во всех упомянутых работах. Однако, эмпирическое изучение распределений, встречающихся на фондовом рынке, в кредитных портфелях банков, других инвестиционных инструментов, показывает существенное отклонение реальных распределений от нормального. В частности, распределения кредитных портфелей обычно обладают ярко выраженной асимметрией и тяжелыми хвостами [1], а в совместных распределениях многих фондовых инструментов обнаружены нелинейные зависимости [2]; эти эффекты несовместимы с предположением нормальности.
Одним из эффективных способов преодоления указанных трудностей является использование аппарата ожидаемой полезности [3]. Эта методология позволяет эффективно обрабатывать асимметричные распределения, а также улавливать некоторые типы нелинейных зависимостей между инструментами. Однако, функционал ожидаемой полезности является линейным относительно операции смеси распределений; это обстоятельство препятствует его использованию в тех случаях, когда индивидуальные предпочтения нелинейны в этом смысле; экспериментальные свидетельства нелинейности такого рода описаны, например, в [4].
Дальнейшее улучшение качества методов принятия инвестиционных решений связано с использованием нелинейных функционалов, появившихся сравнительно недавно [5], а также с использованием индивидуальных предпочтений в качестве исходной информации для построения методов принятия решений [6].
В настоящей работе на простом примере показаны недостатки теории второго порядка, и продемонстрировано применение функционалов ожидаемой полезности и возмущенной вероятности к проблеме формирования инвестиционного портфеля.
Пример распределения инструментов
Рассмотрим случайные величины Хх и Х2 со следующими распределениями Бернулли:P{ X1 = 0} = 0.1, P{Xj = 10} = 0.9, P{ X 2 = 8} = 0.9, P{X2 = 18} = 0.1. (1)
Графики функций вероятности (дискретной "плотности распределения") этих случайных величин приведены на следующем рисунке.
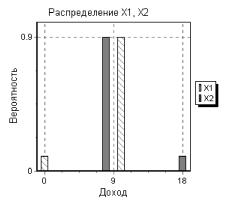
Рис. 1 Распределения инструментов X1 и X2
Этот пример допускает следующую содержательную трактовку. Предположим, что индивидуум обладает состоянием в 10 единиц, которое может быть полностью уничтожено в результате неблагоприятного события, наступающего (в течение рассматриваемого периода времени, например, 1 года) с вероятностью 0.1. Если индивидуум не проявляет никакой финансовой активности, то его состояние через год описывается случайной величиной Xj. Индивидуум может застраховать свое состояние (имущество), уплатив страховую премию в размере 1 единицы, в результате чего его состояние уменьшится до 9 единиц, и не изменится ни при каких случайных обстоятельствах, поскольку убыток, нанесенный страховым событием, будет покрыт страховой компанией, продавшей полис. Предположим теперь, что страховой полис продается только в комплекте с лотерейным билетом стоимостью в 1 единицу, который с вероятностью 0.1 принесет через год выигрыш размером в 10 единиц, а с вероятностью 0.9 - никакого выигрыша. Если индивидуум купит страховку с лотерейным билетом, то его состояние через год будет описываться случайной величиной X2.
Итак, собственник имущества сталкивается с дилеммой: какой из вариантов Х1, X 2 лучше. Большинство людей без колебаний отдают предпочтение проекту с результатом Х2 (некоторые, впрочем, избегают общения с финансовыми организациями, и так же уверено останавливают свой выбор на Х1). Однако, простым подсчетом нетрудно убедиться в том, что математические ожидания и дисперсии этих случайных величин совпадают:
EX 1 = EX2 = 9, DX1 = DX 2 = 9, (2)
так что теории второго порядка не сделают между этими проектами никакого различия, посчитав их эквивалентными, хотя большинство рациональных инвесторов такие проекты четко различают. Осторожные инвесторы, скорее всего, выберут проект X2, в котором отсутствуют резкие отклонения от среднего значения в меньшую сторону (убытки). Далее мы рассмотрим, как производится выбор между этими проектами (по существу, вероятностными распределениями) методом второго порядка и другими методами принятия решений, а также изучим методы построения оптимальных портфелей из инструментов, представленных случайным вектором (X1, X2) :
Xy = yXi + (1 - y)X2, y g Y . (3)
Здесь y обозначает вес первого инструмента в портфеле, а допустимое множество
Y ^ R = (-да, да) может иметь, например, вид [0,1] или R, что определяется существом рассматриваемой задачи. В частности, в задаче выбора проекта, допустимое множество
Y является двухточечным: Y = {0,1} .
Отметим, что распределение дохода портфеля (3) определяется не только маргинальными распределениями (1), но и структурой зависимости компонент случайного вектора (Xj, X2), которую в рассматриваемом простом случае можно описать одним параметром, например, m = P{X1 = 10, X2 = 18}. Значения этого параметра не могут быть произвольными вероятностями, поскольку они должны лежать в границах Фре-ше, которые в данном случае имеют вид 0 < m < 0.1. При m = 0.09 получается распределение с независимыми компонентами, а граничные значения m соответствуют ко-монотонной зависимости (m = 0.1) и антикомонотонной зависимости (m = 0); в последнем случае имеет место Xj + X2 = 18 с вероятностью 1, и корреляция (Xj, X2) равна минус 1. Интересно отметить, что максимальная корреляция, соответствующая значению m = 0.1, оказывается существенно меньшей 1.
Метод второго порядка
Поскольку математические ожидания распределений Х1 и Х2 совпадают, метод второго порядка сводится к минимизации дисперсии распределения Ху, которая имеет видs(y) = DXy = 4(у2 - у)(9 - 50m) + 9.
Минимизация функции s по у дает оптимальное значение у * = 1/2 , как и следовало ожидать в столь симметричной задаче; минимальная дисперсия оказывается равной s(y*) = 50m , и, в частности, равна нулю для антикомонотонных инструментов. Интересно отметить, что диверсификация достигается даже при максимальной положительной зависимости инструментов, имеющей место при m = 0.1; дисперсия оптимального портфеля оказывается равной 5, то есть, почти в 2 раза меньше дисперсии каждого из инструментов. Следующий рисунок иллюстрирует зависимость дисперсии портфеля Ху от веса у при различных значениях параметра m .
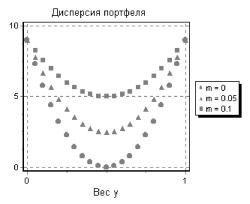
Рис. 2. Критерий оптимальности в задаче второго порядка
Отметим ярко выраженную симметрию критерия оптимальности относительно инструментов Х1, Х2. В описываемых далее методах более высокого порядка такая симметрия появляется только в виде исключения.
Максимизация ожидаемой полезности
Теперь применим для решения задачи метод ожидаемой полезности. Пусть U -некоторая вещественная функция полезности. Если U является возрастающей и строго вогнутой функцией, то есть,U(Хх + (1 - X)у) > XU(х) + (1 - X)U(у), х, у е R, X е (0,1),
то U характеризует инвестора, не приемлющего риск [7]. Примером такого рода функций полезности являются элементы экспоненциального класса
U(x) = (1 - е )/(1 - е ), x е R (4)
при а > 0. При заданной функции полезности U ожидаемая полезность р (X) произвольного проекта (портфеля) X вычисляется по формуле
р (X) = EU(X) = Г U(x)dFx (x),
J—ад
где FX - функция распределения случайной величины X. В частности, для дискретных случайных величин, принимающих значения xk с вероятностями pk = P{X = xk }, k = 1,..., N, справедлива формула
N
р(X)=ZU (xk) Pk. (5)
к=1
Задача выбора проекта сводится к сравнению ожидаемых полезностей р (X1), р (X2) проектов X1, X2. Оказывается, что инвестор, предпочтения которого описываются функцией полезности (4) с каким-либо параметром а > 0, предпочитает проект X2. Не останавливаясь здесь на строгом доказательстве этого факта, проиллюстрируем его графиком зависимости разности р (X2) — р (X1) от значения параметра а .
EU(X2) - EU(X1)
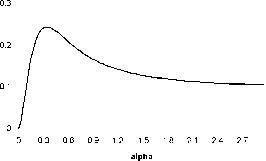
Рис. 3. Зависимость разности ожидаемых полезностей от параметра а
Далее применим метод ожидаемой полезности к задаче формирования портфеля (3), используя функции полезности из экспоненциального класса (4). Здесь требуется найти такое значение веса у , при котором реализуется max EU(Xy). Явное представление для максимизируемой ожидаемой полезности легко получается из (5). Исследуем зависимость решения от значений параметров задачи а , m .
Отметим здесь, что ввиду монотонности U максимизация ожидаемой полезности портфеля эквивалентна максимизации его детерминированного эквивалента, который для произвольной случайной величины X задается посредством
c( X ) = U-'(EU ( X )),
где U-1 - функция, обратная к U . Поэтому характеристики р и c взаимозаменяемы, и использование той или другой из них в каждом конкретном случае определяется соображениями удобства.
Далее, заметим, что предельный случай а = 0 соответствует линейной функции полезности U(х) = х, которая описывает инвестора, нейтрального по отношению к риску [7]. Такой инвестор максимизирует среднее значение дохода портфеля EXy, которое в нашем случае постоянно и равно 9, так что смешивать инструменты в портфеле можно с произвольным весом у .
Другой крайний случай соответствует значению параметра зависимости m = 0. При этом инструменты X1, X 2 оказываются идеально отрицательно коррелированными (то есть, связанными линейной функциональной зависимостью X 2 = 18 - Xj с отрицательным коэффициентом), и смешивание их в портфеле с весом у = 1/2 дает идеально диверсифицированный портфель с вырожденным распределением X1/2 = 9. Такой портфель является оптимальным для произвольного инвестора с функцией полезности из класса (4).
При а > 0 функция полезности (4) описывает инвестора, не приемлющего риск. Если m > 0, то идеальная корреляция инструментов невозможна, и максимизация ожидаемой полезности всегда приводит к нетривиальному решению, на которое оказывает влияние как степень неприятия риска а , так и характер зависимости инструментов, описываемый параметром m .
Далее представлены графики критерия оптимальности (детерминированного эквивалента) рассматриваемой задачи для нескольких значений параметра а .
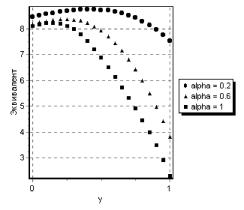
Рис. 4. Детерминированный эквивалент портфеля.
При небольших значениях параметра неприятия риска (а = 0.2) значения целевой функции слабо зависят от веса у, а форма графика близка к симметричной. С увеличением неприятия риска форма графика существенно отклоняется от симметричной, и все большая доля капитала направляется на инвестирование во второй инструмент
X 2.
На следующем рисунке представлены графики зависимости оптимального веса портфеля от параметра а при нескольких значениях параметра m .
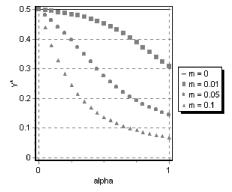
Рис. 5. Зависимость распределения капитала от неприятия риска
Интересно отметить, что за исключением выделенных крайних случаев, доля у всегда оказывается меньше 1/2, то есть, второй инструмент X2 всегда входит в портфель с большим весом, что можно истолковать, как его предпочтительность перед X1 в рамках портфельного анализа.
Метод возмущенной вероятности
Теперь рассмотрим применение метода возмущенной вероятности, который заключается в максимизации функционала возмущенной вероятности на заданном множестве распределений. Для функции распределения F этот функционал вычисляется по одной из формул [5], [6]:п (F) = Г [ - ?(1 - F (х))] + Г g(1 - F (x) = ГF -1 (1 - v)dg(v),
J-ю J0 J0
где монотонная функция g , являющаяся параметром данного функционала, служит для возмущения вероятности, задана на отрезке [0,1], и обладает свойствами g(0) = 0, g(1) = ^ g(х) < х, х е [0,1]. В частности, для дискретного распределения F , описываемого значениями хк, упорядоченными по возрастанию, и вероятностями pk, к = 1,..., N, справедливы формулы [6]:
' fv "I Г v 1 g| Z Pi - s\ Z Pi V i=к ) V i=k+1 )
n I n
Z(x - xk-i )g| Z Piп (F) = ?¦(6) к=1
к=1
__ i=к )
где используется обычное соглашение (пустая сумма полагается равной 0), и введено обозначение х0 = 0. Отметим здесь, что значение этого функционала на распределении
портфеля (3) с необходимостью будет представлять собой кусочно-линейную функцию от веса у.
Рассмотрим класс степенных возмущающих функций вида
g(v) = vа, а > 1.
Здесь параметр а может служить индикатором неприятия риска. При а = 1 значение функционала возмущенной вероятности совпадает со средним значением распределения, так что инвестор, принимающий решения с помощью такого функционала, является нейтральным по отношению к риску. Случай а > 1 соответствует инвестору, не приемлющему риск.
Обратимся к проблеме выбора между проектами. Вычисление значений функционала п на распределениях F1, F2 проектов Х1, Х2 из нашего основного примера без труда производится по формулам (6). Не вдаваясь в технические детали, приведем здесь график разности п (F2 )-n(F1):
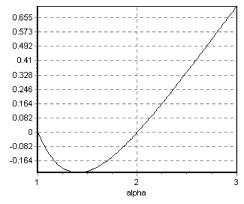
Рис. 6. Разность значений функционала возмущенной вероятности
Видно, что инвесторы, не приемлющие риск, по-разному производят выбор между проектами. Инвесторам, умеренно не приемлющим риск (1 <а < 2), более предпочтительным представляется проект Х1 , тогда как инвесторы с сильным неприятием риска (а > 2) предпочитают X2. Такое явно нелинейное поведение функционала возмущенной вероятности позволяет улавливать с его помощью нелинейные свойства реальных предпочтений, отмечавшиеся в [4].
Рассмотрим теперь задачу формирования инвестиционного портфеля Ху, определенного в (3), из инструментов Х1, X2. Эта задача сводится к максимизации функционала возмущенной вероятности портфеля, как функции веса у . На рисунке 7 представлены графики этого критерия оптимальности при нескольких значениях параметров инвестора а и распределения m. Видно, что оптимальным может быть либо портфель, целиком состоящий из одного инструмента, либо портфель, в котором инструменты представлены равными долями. Этот факт поддается строгому обоснованию при произвольных значениях параметров а > 1, 0 < m < 0.1. В предельном случае инвестора, нейтрального по отношению к риску (а = 1), как и следовало ожидать, функционал возмущенной вероятности принимает постоянное значение 9, совпадающее с ожидаемым доходом портфеля. В предельном случае идеальной обратной коррелиро-ванности инструментов (m = 0), конечно же, оптимальным оказывается портфель с равным представительством инструментов ( у = 0.5 ).
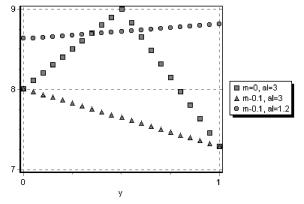
Рис. 7. Возмущенная вероятность портфеля
Заключение
В работе на простом примере показана неспособность классических теорий второго порядка представлять отношение предпочтения лиц, принимающих решения (инвесторов), при наличии асимметричных вероятностных распределений. Представлены и проиллюстрированы методы современного портфельного анализа и принятия решений в условиях вероятностной неопределенности (риска): метод ожидаемой полезности и метод возмущенной вероятности.Высказанная в работе критика в адрес методов второго порядка вовсе не означает отрицание их роли для теории или приложений. В области теории, скажем, модель Марковица и CAPM еще долго будут служить базой для построения более реалистичных, в том числе, неравновесных, моделей. В приложениях использование методов высокого порядка при недостаточном количестве исходных данных может оказаться неоправданным. Разумная стратегия в теоретической части, по-видимому, может быть выражена словами "больше методов хороших и разных", а в плане прикладном - состоит в подборе адекватной модели для каждой конкретной ситуации.
Автор выражает свою искреннюю признательность участникам ФАМ Семинара за многократные обсуждения самых разных вопросов теории риска, которые оказали существенное влияние, в частности, и на содержание настоящей работы.
Литература
1. CreditMetrics - technical document. JPMorgan & Co., New York, 1997, 200p.2. McNeil A.J., Frey R. Estimation of tail-related risk measures for heteroscedastic financial time series: an extreme value approach. J. of Empirical Finance, 7 (2000), 271-300.
3. Нейман Дж. фон, Моргенштерн О. Теория игр и экономическое поведение. М.: Наука, 1970, 708с.
4. Cox L.A. Risk Analysis: Foundations, Models and Methods. Kluwer, 2001, 568 p.
5. Wang S. Premium Calculation by Transforming the Layer Premium Density. ASTIN Bulletin, 26 (1996), 1, 71-92.
6. Новоселов А. А. Математическое моделирование финансовых рисков. Теория измерения. Новосибирск: Наука, 2001, 102 с.
7. Pratt J.W. Risk Aversion in the Small and in the Large. Econometrica, 32 (1964), p. 122136.