Теория автоматического управления
Частотные характеристики разомкнутых систем
Так как полиномы произвольного порядка можно разложить на простые множители, то любую передаточную функцию можно представить в виде произведений простых множителей в числителе и знаменателе или. другими словами, в виде цепочки последовательно соединенных типовых динамических звеньев. Для такой цепочки звеньев (т.е. для разомкнутой однокортнутой системы) передаточная и комплексная частотная функции запишутся в виде:
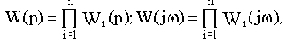
где Wi(p) и
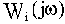
- передаточные и комплексные частотные функ-
ции типовых динамических звеньев.

В этом случае модули и аргументы комплексных функций звеньев и системы связываются следующими соотношениями:
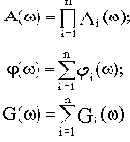
Отсюда вытекает правило построения ЛАЧХ и ЛФЧХ разомкнутой одноконтурной САУ: строят логарифмические характеристики звеньев и затем их графически складывают.
Но для построения асимптотической ЛАЧХ применяют более простой метод, который сформулируем после рассмотрения численного примера.
Пример 2.8.
Построить асимптотическую ЛАЧХ для разомкнутой системы с передаточной функцией
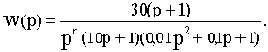
По виду передаточной функции можно заключить, что система состоит из последовательно соединенных n интегрирующих, форсирующего. апериодического и колебательного звеньев.
Рассчитаем сопрягающие частоты (

, а в каждом простом множителе в числителе и знаменателе передаточной функции присутствует Tp):
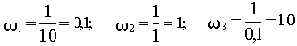
где

- сопрягающая частота апериодического звена,

- сопрягающая частота форсирующего звена,

- сопрягающая частота колебательного звена.
Примем для определенности n=1. Кроме того, будем считать, что коэффициент передачи интегрирующего звена равен коэффициенту передачи разомкнутой САУ, а коэффициенты передачи всех остальных звеньев равны единице.
Определим величину 20lgk : 20lg30=29.
Характеристики звеньев построены на рис.2.18, где соответственно ломаные линии 1,2,3, 4 являются ЛАЧХ интегрирующего, апериодического, форсирующего и колебательного звеньев. Так как коэффициенты передачи всех звеньев, кроме интегрирующего, приняты единичными, то ЛАЧХ этих звеньев при
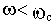
совпадают с осью частот.
Частотные характеристики
Если на вход линейной непрерывной системы (или отдельного звена) подать синусоидальные (гармонические) колебания с постоянными амплитудой и частотной
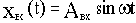
, то после затухания переходных процессов на выходе также возникают синусоидальные колебания
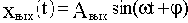
с той же частотой, но с другой амплитудой и сдвинутые по фазе относительно входных колебаний. Как известно из курса "Основы теории цепей, часть 1", синусоидально изменяющиеся величины удобно изображать с помощью комплексных амплитуд. Комплексные амплитуды рассматриваемых здесь входных и выходных колебаний можно записать как
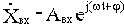
и
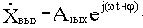
Подавая на вход системы гармонические колебания с постоянной амплитудой, но
различными частотами, на выходе системы тоже получаем гармонические колебания с теми же частотами, но различными амплитудами и фазами относительно входных колебаний.
Введем в рассмотрение отношение комплексных амплитуд выходных и входных колебаний:
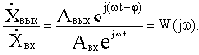
(2.6)
Функция
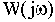
называется
комплексной частотной и получается чисто формально, без каких-либо вычислений, путем замены в выражении передаточной функции переменной р на переменную

:
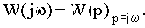
(2.7)
В различных формах записи функцию
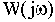
можно представить в следующем виде:
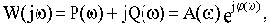
(2.8)
где
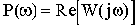
и
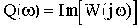
- действительная и мнимая части комплексной частотной функции,

и

- модуль и аргумент комплексной частотной функции.
При фиксированном значении частоты

комплексную частотную функцию можно изобразить вектором на комплексной плоскости, как показано на рис.2.7.
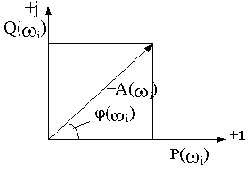
Рис.2.7
Изменение частоты приведет к изменению величины и расположения вектора на комплексной плоскости, а конец вектора опишет некоторую траекторию. Геометрическое место концов векторов комплексной частотной функции при изменении частоты от нуля до бесконечности называется
амплитудно-фазовой частотной характеристикой (АФЧХ).
В свою очередь все величины, представленные в (2.8), являются соответствующими частотными функциями, а построенные по выражениям для функций графики - частотными характеристиками.

называется
вещественной частотной, а

-
мнимой частотной характеристикой.

показывает отношение амплитуд выходного и входного гармонических сигналов при изменении частоты и называется
амплитудной частотной характеристикой.

показывает сдвиг фазы выходного гармонического сигнала относительно входного при изменении частоты и называется
фазовой частотной характеристикой.
Между всеми частотными характеристиками существует непосредственная связь, вытекающая из тригонометрических соотношений и поясняемая рис.2.7.
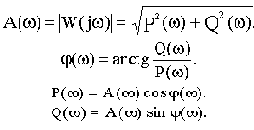
В практических расчетах чаще всего амплитудную и фазовую частотные характеристики изображают в логарифмическом масштабе, что позволяет в значительной степени сократить объем вычислительных работ.
Логарифмической единицей усиления или ослабления мощности сигнала при прохождении его через какое-либо устройство при выражении десятичным логарифмом величины отношения мощности на входе Pвых к мощности на входе Pвх в технике принят бел. Так как мощность сигнала пропорциональна его амплитуде, получим:
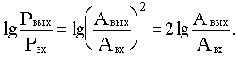
Но так как бел является достаточно крупной единицей усиления (ослабления) мощности (увеличению мощности в 10 раз соответствует 1 Б), то за единицу измерения ее принят децибел 1дБ=0,1 Б.
С учетом этого можно записать:
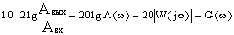
Величина логарифма амплитудной частотной характеристики, выраженная в децибелах
xвх(t)=1(t)
называется
логарифмической амплитудно-частотной характеристикой (ЛАЧХ).
Таким образом, изменению отношения двух амплитуд в 10 раз соответствует изменение усиления на 20 дБ, в 100 раз - на 40 дБ, в 1000 раз - на 60 дБ и т.д.
Вычислим, какому отношению амплитуд соответствует один децибел, два и т.д.
1дБ=20lg(Aвых/Aвх);
lg(Aвых/Aвх)=1/20;
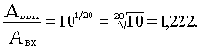
То есть 1 дБ 1,222.
2 дБ ~ (1,222)2=1,259;
3 дБ ~ (1,222)3=1,259;
4 дБ ~ 1,585;
5 дБ ~ 1,778;
6 дБ ~ 1,995 2.
Фазовая частотная характеристика

, построенная в полулогарифмическом масштабе (в координатах: угол

в градусах или радианах и

), называется
логарифмической фазовой частотной характеристикой (ЛФЧХ).
За единицу измерения частоты используется логарифмическая единица декада. Декадой называется интервал частот между какой-либо величиной частоты и ее десятикратным значением.
В логарифмическом масштабе частот отрезок в одну декаду не зависит от частоты и имеет длину, равную
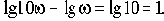
ЛАЧХ и ЛФЧХ строят обычно совместно, используя общую ось абсцисс (ось частот). Начало координат невозможно взять в точке

, так как

. Поэтому начало координат можно брать в любой удобной точке в зависимости от интересующего диапазона частот.
Точка пересечения ЛАЧХ с осью абсцисс называется
частотой среза 
. Ось абсцисс соответствует значению
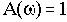
, то есть прохождению амплитуды сигнала в натуральную величину (поэтому еще говорят, что на частоте среза система теряет усилительные свойства).
Из рассмотренных здесь частотных характеристик две можно получить экспериментально-амплитудную

и фазовую Woc(p). Из этих двух экспериментальных остальные частотные характеристики могут быть рассчитаны по соответствующим формулам, например
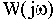
- по формуле (2.8). Кроме того, рассчитав по экспериментальным данным
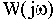
, по (2.7) путем обратной подстановки (заменив

на р) можно получить передаточную функцию, по (2.4) - из передаточной функции дифференциальное уравнение в операторной форме и далее, применив обратное преобразование Лапласа - дифференциальное уравнение (уравнение динамики системы).
К содержанию
Классификация сау
Для ознакомления с основными видами САУ и соответствующей терминологией рассмотрим классификацию систем по ряду существенных с позиции теории автоматического управления признаков.
а). Системы разомкнутые, замкнутые и комбинированные.
В общем виде САУ с одной выходной координатой, одним задающим и одним возмущающим воздействиями представлена на рис.1.1, на котором обозначено:
О - объект управления;
УУ - управляющее устройство (регулятор);
Х - выходная величина, характеризующая состояние объекта;
Y - регулирующее воздействие;
G - задающее воздействие;
F - возмущающее воздействие.
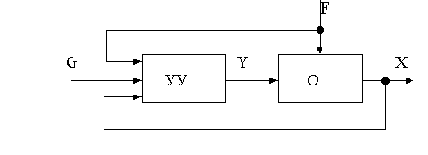
Рис.1.1
На вход УУ помимо задающего воздействия поступает информация о возмущающем воздействии и о текущем реальном значении выходной величины. В соответствии с этим УУ полученную информацию преобразует и формирует регулирующее воздействие.
В частных случаях САУ могут иметь не все представленные связи.
В
разомкнутых САУ выходная величина объекта не измеряется, то есть нет контроля за состоянием объекта. Разомкнутыми они называются потому. что в них отсутствует связь между выходом объекта и входом управляющего устройства.
Возможны варианты, в которых УУ измеряет только задающее воздействие G, либо задающее и возмущающее воздействие F. В первом варианте принято говорить, что управление осуществляется
по задающему воздействию, во втором -
по возмущающему.
При реализации управления по задающему воздействию команды G путем изменения Y приводят к соответствующим изменениям выходной величины Х. Точность соответствия Х и G определяется стабильностью параметров УУ и О, а также величиной возмущения.
В САУ с управлением по возмущающему воздействию (такие САУ называют еще системами, реализующими
принцип управления по возмущению) регулирующее воздействие Y формируется таким, чтобы скомпенсировать отклонение выходной величины Х, вызванное измеряемым возмущением F. Для повышения точности необходимо учитывать все возможные возмущения. Практически большинство возмущений трудно измерить и преобразовать в нужный тип сигнала. Кроме того, измерение нескольких возмущений усложняет схему САУ.
В
замкнутых САУ на вход УУ подаются задающее воздействие G и выходная величина объекта Х. Исходя из величины G управляющее устройство определяет соответствующее требуемое значение Х0 и, имея информацию о текущем значении Х, обеспечивает необходимое соответствие между Х и G путем воздействия на объект.
В такой САУ управляющее устройство стремится ликвидировать все отклонения Х от предписанного Х0 независимо от причин, вызывающих эти отклонения, включая любые возмущения и внутренние помехи.
САУ такого типа представляют собой замкнутый контур, образованный О и УУ. Управляющее устройство создает обратную связь вокруг объекта, связывая его выход со входом. Замкнутые САУ называют поэтому еще системами
с обратной связью или системами, реализующими
принцип управления по отклонению. Именно системы с обратной связью представляют основной тип САУ.
При использовании в одной системе принципов управления по отклонению и по возмущению получают
комбинированную САУ. В этом случае повышается качество управления, так как увеличивается информация о состоянии объекта и внешней среды.
Проиллюстрируем (на качественном уровне, без количественной оценки) преимущества замкнутой САУ над разомкнутой по задающему воздействию на примере генератора постоянного тока, управляемого по цепи возбуждения. Схема разомкнутой системы приведена на рис.1.2.
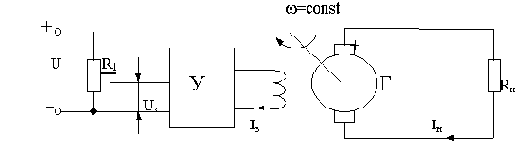
Рис.1.2
Предположим, что обеспечено вращение вала генератора Г с неизменной угловой скоростью

, генератор работает на линейном участке кривой намагничивания, функциональный усилитель У обеспечивает линейную зависимость тока возбуждения Iв от задающего напряжения Uз.
Управлять выходной величиной - напряжением Uн, прикладываемым к сопротивлению нагрузки Rн , можно, изменяя величину Uз путем передвижения движка потенциометра R1.
В качестве возмущающего воздействия рассмотрим изменение величины нагрузки, т.е. тока Iн.
По второму закону Кирхгофа
Uн=E-Iнrвн,
где Е - э.д.с. генератора,
rвн- внутреннее сопротивление генератора.
Если ток нагрузки изменяется от 0 до какого-то максимального значения

, то изменение выходного напряжения

при этом составит величину (при условии, что Uз=const)
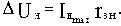
Если мощность генератора соответствует мощности нагрузки, то rвн относительно Rн составляет величину, которой нельзя пренебречь, в результате

относительно Е является величиной существенной, т.е. изменение нагрузки при неизменном задающем воздействии значительно влияет на выходное напряжение.
Далее замкнем обратную связь, т.е. подадим часть выходного напряжения, снимаемого с резистора R3 делителя напряжения на резисторах R2 и R3 и обозначенного Uос, на вход усилителя У, как показано на рис.1.3. Причем полярность напряжений должна быть такой, как показано на рис.1.3 без скобок.
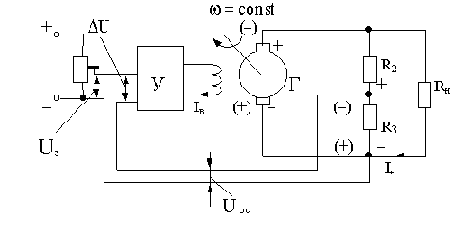
Рис.1.3
Пусть эта схема находилась в каком-то исходном установившемся состоянии, при котором
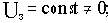
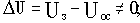
Rн=const; Iн=const; Uн=const.
Далее предположим, что в схеме произошло возмущение - скачком увеличилось сопротивление нагрузки и, следовательно, уменьшился ток Iн. Как схема отреагирует на это возмущение?
Вначале напряжение Uн увеличится, так как уменьшится падение напряжения на внутреннем сопротивлении генератора. Следовательно, увеличится Uос, уменьшится

(Uз осталось неизменным), пропорционально уменьшится Iв, уменьшится Е, уменьшится и выходное напряжение Uн. Указанные процессы будут происходить не мгновенно, а за какое-то конечное время, по истечении которого выходное напряжение с какой-то точностью вернется к исходному значению. Если бы произошло не уменьшение, а увеличение тока нагрузки, то все величины изменялись бы в противоположную сторону.
В рассмотренной схеме изменение тока нагрузки (возмущающего воздействия) уже не приводит к значительному изменению выходного напряжения.
Но рассмотрим еще один аспект: как бы работала схема. если бы генератор подключили с противоположной полярностью (указана на рис.1.3 в скобках).
При увеличенииRн и уменьшении Iн вначале Uн увеличится, как и в предыдущем случае. Увеличится и Uос, но теперь
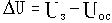
, таким образом увеличится

, увеличатся Iв и Е, следовательно еще больше увеличится Uн. Таким образом, вызванное на начальном этапе после возмущения увеличение Uн приводит к увеличению

, которое в свою очередь увеличивает Uн и т.д. Схема стала неработоспособной (в первом случае обратная связь была отрицательной, во втором - положительной).
Одна из задач теории автоматического управления - дать точную количественную оценку всем рассмотренным в настоящем примере явлениям.
б). Системы линейные и нелинейные.
Линейной называется система, которая описывается только линейными уравнениями. Чтобы система была нелинейной, достаточно иметь в ее составе хотя бы одно нелинейное звено.
Для линейных САУ применим принцип суперпозиции: реакция системы на любую комбинацию внешних воздействий равна сумме реакций на каждое из этих воздействий, поданных на систему порознь.
Необходимо отметить, что реальные линейные системы являются таковыми лишь в определенном диапазоне изменения воздействий. Если не ограничивать диапазон изменения воздействий, то любая САУ становится нелинейной.
в). Системы непрерывного и дискретного действия.
Непрерывная система состоит из звеньев, выходная величина которых изменяется плавно (без скачков) при плавном изменении входного воздействия. Дискретная САУ должна содержать хотя бы одно звено дискретного действия. Под звеном дискретного действия понимается звено, у которого выходная величина изменяется скачками при плавном изменении входной.
г). Системы стационарные и нестационарные.
Стационарной называется система, все параметры которой не изменяются во времени. Нестационарная система - это система с переменными во времени параметрами. При математическом описании такой системы некоторые коэффициенты являются функциями времени.
В качестве примера нестационарной системы можно привести самолет. В полете по мере расхода горючего масса самолета уменьшается.
д). Одномерные и многомерные САУ.
Разделение на данном уровне классификации производится по числу выходных координат объекта управления.
Пример одномерной системы - источник питания постоянного тока (выходная координата одна - среднее значение напряжения), двухмерной - источник питания переменного тока (выходных координат две - частота и эффективное значение напряжения), трехмерной - радиолокационная станция слежения за летательными аппаратами (выходных координат три - дальность, угол места, азимут).
е). Системы стабилизации, программного управления и следящие.
Системы стабилизации характеризуются неизменностью задающего воздействия. Задача таких систем - поддержание с допустимой ошибкой выходной величины при наличии возмущающих воздействий.
Системы программного управления отличаются тем, что задающее воздействие изменяется по заранее установленному закону.
В следящих системах задающее воздействие также является величиной переменной, но заранее закон его изменения неизвестен. Источником сигнала является внешнее явление.
Таким образом, для систем стабилизации G=const, для следящих систем и систем программного управления G=var.
ж). Системы оптимальные и неоптимальные (обыкновенные).
В оптимальных системах должно обеспечиваться оптимальное значение какого-либо из параметров функционирования. Но так как связь между отдельными параметрами обычно противоречивая, то на остальные параметры накладывается ограничение (значение их должно быть не хуже заданного уровня). В обыкновенных системах указанная задача оптимизации не ставится.
В завершение вводного раздела введем понятие
функциональной схемы (не путать со схемой электрической функциональной !), принятое в теории автоматического управления. При составлении функциональной схемы система разбивается на такие узлы, каждый из которых несет законченное функциональное назначение (сложность каждого из таких узлов при этом значения не играет). Выделенные таким образом узлы на функциональной схеме соединяются линиями связи с указанием направления распространения сигналов.
Какими бы ни были системы автоматического управления (хотя бы в соответствии с представленной здесь классификацией, физическим принципом действия, областью применения и т.д.), они в целом имеют одну и ту же функциональную схему, но только некоторые элементы могут отсутствовать или, наоборот, повторяться. Такая обобщенная функциональная схема представлена на рис.1.4.
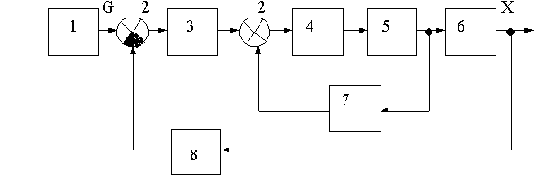
Рис.1.4
Здесь обозначено: 1- задающее устройство, формирующее задающее воздействие G; 2 - сумматор (сектор круга зачерняется, если подходящий к нему сигнал имеет знак "минус", например, реализуется отрицательная обратная связь); 3 - последовательное корректирующее устройство; 4 - усилитель; 5 - исполнительный элемент; 6 - объект управления; 7 - местная обратная связь (параллельное корректирующее устройство); 8 - главная обратная связь.
К содержанию
Критерии качества переходного процесса
Исчерпывающее представление о качестве переходного процесса дает, естественно, сама кривая процесса. Однако при разработке САУ необходимо иметь возможность судить об основных показателях качества переходного процесса без построения их кривых, по каким-либо косвенным признакам, которые определяются более просто и, кроме того, позволяют связать показатели качества непосредственно со значениями параметров САУ. Такие косвенные признаки называются
критериями качества переходного процесса.
Существуют три группы критериев качества: частотные, корневые и интегральные.
Наибольшее распространение получили
частотные критерии, в основу которых положено использование частотных характеристик. Для иллюстрации возможности оценки качества переходного процесса по частотным характеристикам установим точную аналитическую зависимость между переходной характеристикой h(t) и вещественной частотной характеристикой (ВЧХ) P(

).
На основании возможности разложения функции времени в ряд Фурье единичное ступенчатое воздействие можно представить в виде выражения
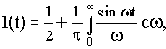
то есть суммы постоянной составляющей и бесконечного числа синусоид частотой

и амплитудой

при изменении

от 0 до

.
Уравнение АФЧХ имеет вид:
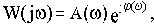
где
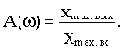
Если на вход системы подать 1(t), то каждому из входных синусоидальных колебаний
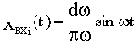
будет соответствовать колебание на выходе [с амплитудой
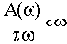
, сдвинутое по фазе относительно входного колебания на угол

(

) ]
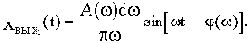
Постоянной составляющей

на входе будет соответствовать постоянная составляющая
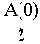
на выходе.
Результирующее значение выходной величины:
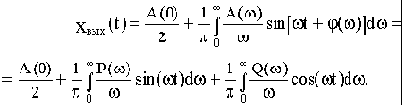
(4.3)
Так как воздействие 1(t) подается в момент t=0, то при t<0:
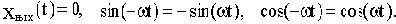
Уравнение (4.3) при подстановке значения (-t) вместо t примет вид:

(4.4)
Вычтем из уравнения (4.3) уравнение (4.4):
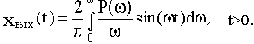
(4.5)
Пользуясь зависимостью (4.5), можно составить предварительное приближенное суждение о качестве переходной характеристики по виду ВЧХ. Различные типы ВЧХ представлены на рис.4.5.
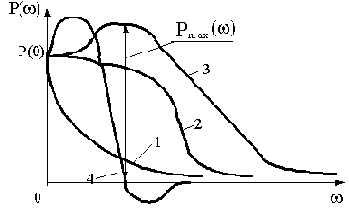
Рис.4.5
Основные положения оценки качества по ВЧХ сводятся к следующему:
1) приблизительно одинаковым частотным характеристикам соответствуют приблизительно одинаковые переходные характеристики;
2) значение переходной характеристики h(t) в установившемся состоянии подчиняется следующему соотношению
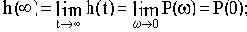
3) если ВЧХ имеет вид кривой 1 (см. рис.4.5), переходная характеристика будет монотонной;
4) для ВЧХ, имеющей вид кривой 2, характерно наличие перерегулирования у переходной характеристики величиной


18%;
5) наличие экстремума ВЧХ (кривая 3) увеличивает колебательность до величины

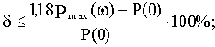
6) наличие экстремума ВЧХ в отрицательной области (кривая 4) проводит к дополнительному росту колебательности;
7) длительность переходного процесса tп оценивается приблизительно по величине интервала существенных частот

cщ (в этом интервале Р(

)

0,05 Р(0), причем
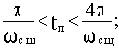
8) острый пик ВЧХ при
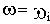
свидетельствует о медленно затухающих колебаниях с чатотой, близкой к
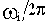
;
9) если при некоторой частоте ВЧХ претерпевает разрыв, то САУ является неустойчивой.
Колебательность переходной характеристики можно оценить по величине относительного максимума амплитудной частотной характеристики А(

), примерный вид которой представлен на рис.4.6.
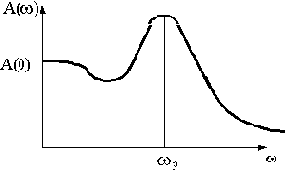
Рис.4.6
Величина относительного максимума называется показателем колебательности М и определяется отношением
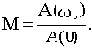
При М<1 переходная характеристика неколебательна. Чем больше М, тем больше колебательность. При М

- незатухающие колебания. Оптимальным обычно считается М=1,3-1,5. При этом переходная характеристика имеет слабую колебательность с частотой, близкой к

.
Вследствие предельной простоты построения ЛАЧХ удобно пользоваться именно этой характеристикой. Информацию здесь несет среднечастотная часть характеристики. При частоте среза

наклон ЛАЧХ должен составлять минус 20 дБ/дек, а значение

определяется временем переходного процесса tп и перерегулированием

:

где k берется по графику на рис.4.7 в зависимости от величины

.
Сопрягающие частоты ЛАЧХ слева и справа от

, как показано на рис.4.8, рассчитываются по выражениям:
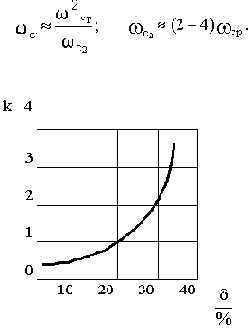
Рис.4.7
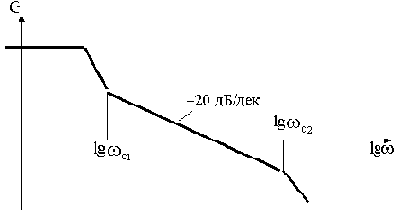
Рис.4.8
Величины наклонов ЛАЧХ слева от

и справа от

на качество переходного процесса почти не влияют.
Группа
корневых критериев основана на оценке качества переходного процесса по значениям полюсов и нулей передаточной функции САУ.
Заметим, что при исследовании устойчивости нас интересовали лишь полюсы, здесь же необходимо учитывать и нули. Только в частном случае, когда нулей нет, качество переходного процесса определяется только полюсами. Начнем рассмотрение именно с такого случая.
Переходной процесс в устойчивой системе распадается на затухающие и колебательные составляющие. Если найти длительность самой длительной составляющей и величину колебательности самой колебательной составляющей, то по ним можно оценить верхние пределы величин длительности и колебательности всего переходного процесса.
Время затухания отдельной составляющей определяется величиной
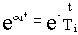
,
где
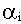
- действительная часть i-го корня характеристического уравне-
ния,
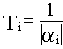
- постоянная времени затухания.
Можно считать, что длительность i-ой составляющей переходного процесса
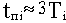
, то есть длительность составляющих переходного процесса обратно пропорциональна абсолютному значению действительной части корней характеристического уравнения.
Абсолютная величина
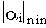
называется степенью устойчивости и обозначается
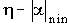
.
При этом длительность переходного процесса будет
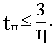
Термин “степень устойчивости” связан с тем, что геометрически

- есть расстояние от мнимой оси, являющейся границей устойчивости, до ближайшего корня (см. рис.3.1).
Колебательность колебательной составляющей переходного процесса
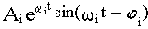
определяется отношением соседних максимумов:
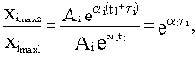
где t1- момент появления первого максимума i-й составляющей пере-
ходной характеристики,
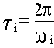
- период колебаний данной составляющей.
Таким образом, колебательность равна
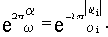
Следовательно, мерой колебательности является отношение
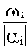
: чем оно больше, тем больше колебательность составляющей. Наиболее колебательной является составляющая, у которой это отношение максимально. Соответствующая величина обозначается
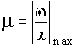
и называется степенью колебательности.
В комплексной плоскости корень, определяющий наиболее колебательную составляющую, соответствует наибольшему значению угла
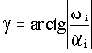
между лучом, направленным через корень из начала координат, и действительной отрицательной полуосью.
Далее отметим влияние на качество переходного процесса наличия нулей передаточной функции. Положительные члены полинома числителя передаточной функции приведут к повышению колебательности и убыстрению переходного процесса, а отрицательные - к затягиванию переходного процесса.
Интегральными критериями
качества называются такие, которые одним числом оценивают и величины отклонений, и время затухания переходного процесса. Для пояснения используем рис.4.9.
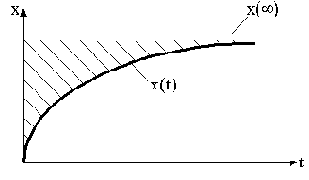
Рис.4.9
Обозначим отклонение выходной величины от нового установившегося значения
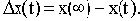
Для монотонного процесса интегральной оценкой может служить заштрихованная площадь над кривой переходного процесса (см. рис.4.9), то есть
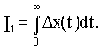
Интеграл I1 называется линейной интегральной оценкой. Процесс будет тем лучше, чем меньше число I1.
Однако такая оценка не годится для колебательного процесса, так как площади, расположенные ниже и выше прямой х(

), будут иметь разные знаки. Поэтому по минимуму величины I1 наилучшим оказался бы процесс с незатухающими колебаниями.
В связи с этим в общем случае принимают квадратичную интегральную оценку качества в виде
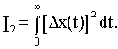
Целесообразность применения интегральных критериев заключается в том, что в литературе имеются формулы, выражающие I2 (или другие интегральные оценки) непосредственно через коэффициенты дифференциального уравнения САУ.
Интегральные критерии качества используются для определения оптимальных значений варьируемых параметров по минимуму значения соответствующей интегральной оценки.
Применяются интегральные критерии обычно в теории оптимальных систем.
К содержанию
Критерий устойчивости гурвица
По этому критерию условия устойчивости сводятся к выполнению ряда неравенств, связывающих коэффициенты уравнения системы. Пусть характеристический полином САУ будет (характеристический полином определяет левую часть уравнения САУ, т.е. знаменатель передаточной функции):
A(p)=anpn+an-1pn-1+...+a1p+a0
Пологая an>0(если anотрицательно, то это условие можно выполнить, умножив весь полином на минус единицу), составляется из коэффициентов A(p)определитель Гурвица:

В первой строке пишутся коэффициенты с условно нечетными индексами (т.е. коэффициенты с индексами n минус нечетное число, где n - порядок характеристического полинома), во втором - с условно четными (т.е. n минус четное число). Концы строк заполняются нулями так, чтобы матрица имела n столбцов. Третья и четвертая строки получаются сдвигом первых двух на одно место вправо и т.д. ( всего строк - n).
Условия устойчивости заключаются в требовании положительности определителя Гурвица и всех его диагональных миноров. Из этого правила можно вывести более удобное для практического применения: САУ устойчива, если положительны все коэффициенты характеристического полинома и предпоследний диагональный минор определителя Гурвица (справедливо для систем не выше четвертого порядка).
Выведем выражение для расчета предпоследнего диагонального минора

систем третьего и четвертого порядка.
Для систем третьего порядка (n=3):
A(p)=a3p3+a2p2+a1p+a0;
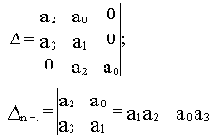
(3.1)
Для систем четвертого порядка (n=4):
A(p)= a4p4+a3p3+a2p2+a1p+a0;

(3.2)
Перед дальнейшим изложением материала уточним терминологию и покажем, как без излишних вычислений составляется характеристический полином замкнутой САУ по заданной структурной схеме. Для пояснений воспользуемся схемой на рис.3.2.
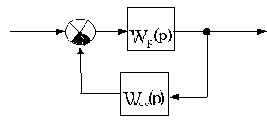
Рис.3.2
Пусть передаточная функция разомкунтой системы Wp(p) и цепи обратной связи Woc(p) будут:
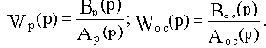
Последовательное соединение элементов с передаточными функциями Wp(p) и Woc(p) даст разомкнутую цепь звеньев замкнутой САУ с передаточной функцией Wр.ц.(p), которую будем называть передаточной функцией разомкнутой цепи:
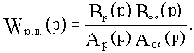
Через принятые обозначения определим передаточную функцию замкнутой САУ:
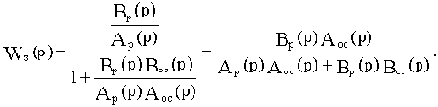
Отсюда характеристический полином замкнутой САУ будет:
Aз(p)=Ap(p)Aoc(p)+Bp(p)Boc(p).(3.3)
То есть, характеристический полином замкнутой САУ равен сумме числителя и знаменателя передаточной функции разомкнутой цепи.
В качестве примера рассмотрим САУ со структурной схемой, приведенной на рис.3.3, для которой необходимо определить соотношение параметров, обеспечивающих устойчивость.
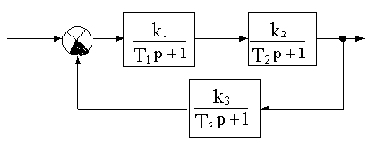
Рис.3.3
Составим характеристический полином замкнутой САУ в соотвествии с (3.3):
Aз(p)=(T1p+1)(T2p+1)(T3p+1)+k1k2k3.(3.4)
Запишем характеристический полином в общем виде:
Aз(p)=a3p3+a2p2+a1p+a0;
где
a3=T1T2T3, a2=T1T2+T2T3+T3T1,
a1=T1+T2+T3, a0=k1k2k3+1=k+1.
Условия устойчивости сводятся к следующим неравенствам:
T1T2T3>0, T1T2+T2T3+T3T1>0,
T1+T2+T3>0, k>0
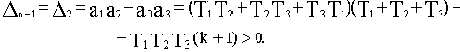
Первые три неравенства интереса не представляют, если мы ограничиваем рассмотрение положительными значениями постоянных времени. Четвертое неравенство показывает лишь, что в случае ошибки и включения вместо отрицательной связи положительной система станет неустойчивой.
Реальные ограничения на значения параметров системы накладывает последнее неравенство. Его удобнее записать в другом виде, поделив левую часть на T1T2T3:
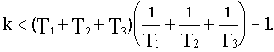
Это неравенство показывает, что устойчивость САУ в конце концов нарушится при неограниченном увеличении коэффициента передачи k при любых значениях постоянных времени.
Предельное по величине значение k, при котором САУ теряет устойчивость, принято называть
критическим (или граничным). Для рассматриваемого примера:
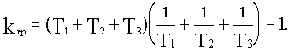
(3.5)
Значение граничного коэффициента передачи зависит не от абсолютных значений постоянных времени , а от их отношения.
Для рассмотренной здесь структуры при равенстве всех постоянных времени, преобразовав соотношение (3.5) к виду
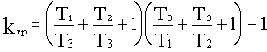
легко определить, что kгр=8. Для данной структуры найденное значение kгр является минимальным. Чем больше будут различаться постоянные времени, тем больше будет величина kгр.
С помощью критериев устойчивости можно строить
области устойчивости.
При проектировании САУ ряд параметров и звеньев являются заданными, так как они определяются требованиями технологического процесса и конструктивными особенностями объекта регулирования. В то же время имеется несколько параметров, которые можно менять в определенных пределах. Для определения влияния значений каких-либо варьируемых параметров на устойчивость строят области устойчивости системы в пространстве этих варьируемых параметров.
Уравнения границ области устойчивости получаются из условий устойчивости, если заменить в них неравенства на равенства (это соответствует нахождению системы на границе устойчивости).
В общем случае границы области устойчивости по критерию Гурвица строятся по следующим уравнениям:
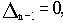
an=0, a0=0
Первое уравнение соответствует наличию у характеристического уравнения пары сопряженных мнимых корней, второе равенство соответствует наличию нулевого корня, а третье - наличию бесконечного корня.
Для САУ, уже рассмотренной выше (см. рис.3.3), зададим варьируемыми параметрами общий коэффициент передачи разомкнутой цепи k и постоянную времени T1. Уравнениями для построения границ области устойчивости будут:
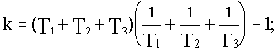
k+1=0;
T1=0.
Границы области устойчивости изображены на рис.3.4. Около границ принято наносить штриховку в сторону области устойчивости.
Каждая точка внутри области устойчивости определяет комбинацию варьируемых параметров k и T1, при которых система устойчива. Причем, если система в пространстве всех своих параметров не имеет области устойчивости, она называется структурно неустойчивой. Для получения устойчивости в этом случае необходимо изменить структуру.
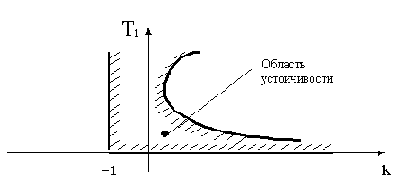
Рис.3.4
Пример 3.1.
Определить устойчивость САУ, структурная схема которой приведена на рис.3.5, воспользовавшись критерием устойчивости Гурвица.
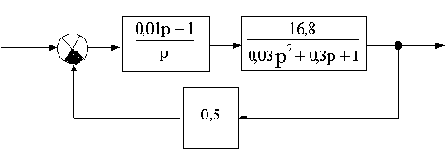
Рис.3.5
Для установления устойчивости определим граничное значение коэффициента передачи и сравним его с имеющимся значением коэффициента.
Передаточная функция разомкнутой цепи
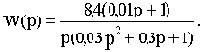
В соответствии с (3.3) характеристический полином замкнутой системы
Aз(p)=p(0,03p2+0,3p+1)+k(0,01p+1)=
=0,03p3+0,3p2+(1+0,01k)p+k=a3p3+a2p2+a1p+a0,
где a3=0,03; a2=0,3; a1=1+0,01k; a0=k.
Так как система имеет третий порядок, то она будет находится на границе устойчивости при равенстве нулю выражения (3.1):
a1a2-a0a3=0,3(1+0,01kгр)-0,03kгр=0
Отсюда находим kгр=11,1
Коэффициент передачи разомкнутой цепи k=8,4 меньше, чем kгр Следовательно, система в замкнутом состоянии устойчива.
К содержанию
Критерий устойчивости михайлова
Основан также на рассмотрении характеристического полинома.
Подставим в этот полином вместо р мнимую переменную

. Получим комплексную функцию
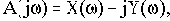
где
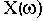
- действительная часть, полученная из членов А(р), содержащих четные степени р;

- мнимая часть, полученная из членов А(р) с нечетными степенями р.
Изобразим А(

) в виде графика в комплексной плоскости, как показано на рис.3.6.
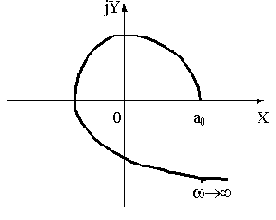
Рис.3.6
Этот график принято называть годографом Михайлова. Каждому значению

соответствуют определенные значения Х(

) и Y(

) и определенная точка на плоскости. При

=0 функция А(

)=а0, т.е. годограф начинается на действительной оси. При

функция А(

) тоже неограниченно возрастает.
Сформулируем критерий Михайлова: система устойчива, если годограф А(

), начинаясь на действительной положительной полуоси, огибает против часовой стрелки начало координат, проходя последовательно n квадрантов, где n - порядок системы.
Представленный выше годограф (см. рис.3.6) соответствует устойчивой САУ четвертого порядка.
Годограф Михайлова можно строить по точкам, изменяя частоту от нуля до бесконечности с определенным шагом и вычисляя каждый раз значение А(

).
Можно поступить по другому: найти точки пересечения годографа с осями и соединить их плавной линией. Для этого, определив из уравнения Х(

)=0 значения частот, соответствующих точкам пересечения годографа А(

) с мнимой осью, подставляют их в выражение Y(

). В результате получают соответствующие координаты. Аналогично находят точки пресечения А(

) с действительной осью, приравнивая нулю мнимую часть Y(

).
Собственно, после того, как найдены значения

, при которых годограф А(

) пересекает оси координат, то есть нули Х(

) и Y(

), нет необходимости строить сам годограф.
Из формулировки критерия следует, что устойчивость имеет место, если нули Х(

) и Y(

) чередуются с ростом

, начиная с

=0, когда Y(

)=0, а Х(

)>0.
Выше отмечалось, что условием нахождения САУ на границе устойчивости является попадание корня характеристического уравнения на мнимую ось плоскости корней. Но если характеристическое уравнение А(р)=0 имеет корень
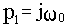
, то удовлетворяется равенство
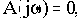
откуда получаем
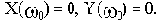
Графически это означает попадание одной точки годографа Михайлова в начало координат.
Таким образом. условием нахождения САУ на границе устойчивости является прохождение годографа Михайлова через начало координат (при какой-то частоте

. Физический смысл величины
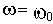
- частота колебаний системы на границе устойчивости).
Но для нахождения на границе устойчивости должен быть пропущен лишь один квадрант. Другими словами, очертание кривой Михайлова на границе устойчивости должно быть таким, чтобы малой деформацией ее в начале координат можно было удовлетворить критерию Михайлова. Так, график на рис.3.7, а соответствует нахождению САУ на границе устойчивости, а график на рис.3.7, б - неустойчивости.
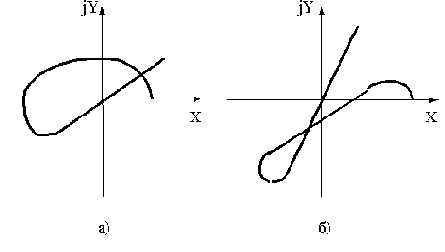
Рис.3.7
В качестве примера определим граничное значение коэффициента передачи kгр для рассмотренной выше САУ (см. рис.3.3).
Запишем функцию для построения годографа Михайлова, подставив в характеристический полином (3.4) вместо р мнимую переменную

:
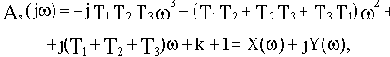
где
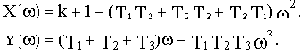
При нахождении САУ на колебательной границе устойчивости годограф Михайлова проходит через начало координат при частоте
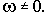
Поэтому при k=kгр:
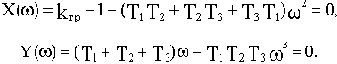
Из второго уравнения находим значение квадрата частоты, при котором годограф проходит через начало координат:
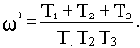
Подставив это значение в первое уравнение, получим
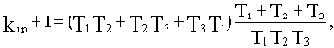
или окончательно
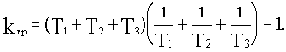
Получили, естественно, тот же результат, что и по критерию Гурвица.
Критерий Михайлова широко используется для построения областей устойчивости. Уравнения границы устойчивости в пространстве двух варьируемых параметров

и

, согласно этому критерию, имеют вид:
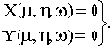
Исключив из этих уравнений параметр

, можно получить уравнение границы устойчивости, связывающее входящие в выражения
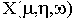
и
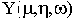
варьируемые параметры

и

. Для определенности такой метод определения границы устойчивости будем называть “по критерию Михайлова”.
Собственно, так мы и поступили в только что рассмотренном примере.
С другой стороны, можно построить границы устойчивости по приведенной системе уравнений, используя

как параметр, который изменяют от 0 до

. Каждому значению

при этом соответствует определенная точка границы устойчивости. Этот метод получения границы устойчивости принято называть методом D - разбиения.
Пусть характеристическое уравнение САУ в общем виде будет следующее:
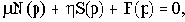
где N(p),S(p),F(p)- полиномы от р.
После подстановки
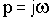
получим:
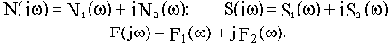
Исходное характеристическое уравнение распадается на два:
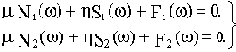
(3.6)
Решим эту систему уравнений:
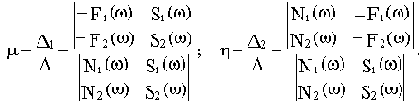
(3.7)
Построенный по выражениям (3.7) график называется кривой D - разбиения плоскости (

,

). При движении по кривой D - разбиения в сторону возрастания

штриховку наносят слева, если определитель

положителен, и справа - если отрицателен.
В результате получают область. которая может претендовать на область устойчивости. В заключение произвольную точку этой области проверяют любым из критериев устойчивости.
Пример 3.2.
Решить задачу примера 3.1 с использованием критерия Михайлова.
Подставим в выражение характеристического полинома вместо р комплексную переменную

:
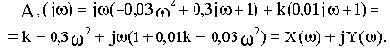
Для определения устойчивости не будем строить годограф Михайлова, а рассчитаем величину kгр, т.е. поступим аналогично примеру 3.1.
Условие нахождения САУ на границе устойчивости:
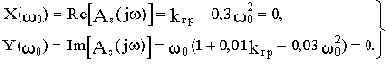
Корень второго уравнения
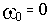
отбрасываем, т.к. для нахождения системы на границе устойчивости годограф Михайлова должен пройти через начало координат при
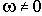
.
Тогда из второго уравнения определяем
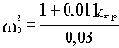
и подставляем в первое:
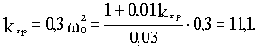
Получили тот же результат, что и в примере 3.1.
Пример 3.3.
По критерию устойчивости Михайлова определить устойчивость САУ по заданному характеристическому полиному:
A(p)=3*10-4p5+5*10-3p4+0,1p3+0,5p2+0,9p+1
Годограф Михайлова построим примерно, определив координаты пересечения его с осями координат.
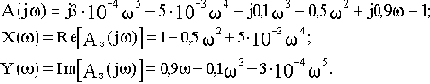
С учетом того, что годограф Михайлова строится при изменении

от 0 до +

, определим положительные корни уравнения X(

)=0:
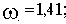
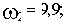
и неотрицательные корни уравнения Y(

)=0:
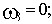
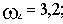
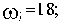
Координаты пересечения годографа Михайлова с осями координат (в порядке возрастания частоты):
1)
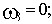
Y=0; X=1;
2)
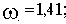
X=0; Y=0,9*1,41-0,1*1,413+0,0003*1,415=0,99;
3)
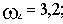
Y=0; X=1-0,5*3,22+0,005*3,24=3,6;
4)
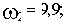
X=0; Y=0,9*9,9-0,1*9,93+0,0003*9,95=-59,59;
5)
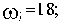
Y=0; X=1-0,5*182+0,005*184=364.
Примерный вид годографа Михайлова для полученных данных показан на рис.3.8. Исследуемая система устойчива.
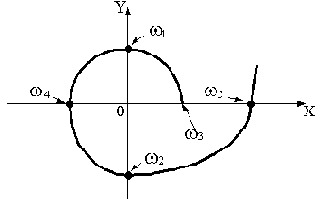
Рис.3.8
Пример 3.4.
Для САУ, структурная схема которой приведена на рис.3.3, определить область устойчивости методом D- разбиения. Варьируемые параметры T3 и k3. Значения неварьируемых параметров:
T1=0,1; T2=1; k1=2; k2=5.
Характеристический полином замкнутой САУ:
Aз(p)=(T1p+1)(T2p+1)(T3p+1)+k1k2k3=T1T2T3p3+
+(T1T2+T2T3+T3T1)p2+(T1+T2+T3)p+k1k2k3+1.
Представим последнее выражение в следующем виде:
Aз(p)=T3N(p)+k3S(p)+F(p).
Aз(p)=T3[T1T2p3+(T1+T2)p2+p]+k3(k1k2)+
+[T1T2p2+(T1+T2)p+1].
Сделаем подстановку
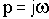
:
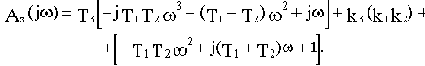
Выделим вещественную и мнимую части. представив их в следующем виде:

Рассчитаем для последней системы уравнений определители
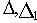
и
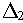
:
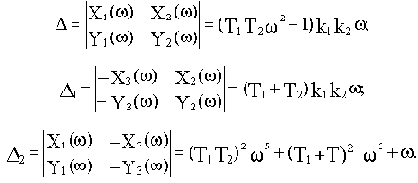
Найдем выражения для T3 и k3:
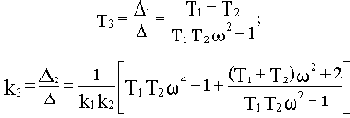
Подставляя численные значения, получим:
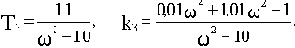
Результаты расчетов границы области устойчивости по последним выражениям сведены в таблицу. Еще две границы получаются в результате приравнивания нулю коэффициента характеристического полинома при p3 (T3=0) и свободного члена характеристического полинома:
k1k2k3+1=0,
k3=-1.
Область устойчивости построена на рис.3.9.
Таблица
|

|
0
|
1
|
2
|
3
|
4
|
5
|
7
|
10
|
15
|
20
|
Т3
|
-1,1
|
-1,2
|
-1,83
|
-11
|
1,83
|
0,73
|
0,28
|
0,12
|
0,051
|
0,028
|
k3
|
-0,1
|
-0,22
|
-0,86
|
-10,9
|
3,29
|
2,17
|
1,91
|
2,24
|
3,42
|
5,14
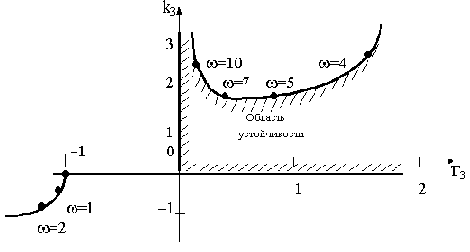
Рис.3.9
К содержанию
Критерий устойчивости найквиста
Предназначен для анализа устойчивости замкнутых систем.
Для случая, если разомкнутая цепь устойчива, условия устойчивости замкнутой САУ сводится к требованию, чтобы амплитудно-фазовая частотная характеристика (АФЧХ) разомкнутой цепи не охватывала точку (- 1, j0).
Если АФЧХ разомкнутой цепи Wрц( ) проходит через точку (- 1, j0) , то можно записать
) проходит через точку (- 1, j0) , то можно записать
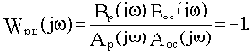
Но это возможно в том случае, если
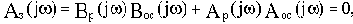
то есть годограф Михайлова замкнутой САУ проходит через начало координат.
Таким образом, если АФЧХ разомкнутой цепи проходит через точку (- 1, j0), то замкнутая САУ будет находится на границе устойчивости.
На рис.3.10 приведены две АФЧХ. Кривая 1 соответствует устойчивой САУ, кривая 2 - нахождению САУ на границе устойчивости.
Если, например, уменьшить коэффициент передачи в неустойчивой САУ, то ее АФЧХ будет сжиматься к началу координат, в результате чего система станет, наконец, устойчивой. Аналогично этому происходит и обратное.
Для САУ, имеющих неустойчивую разомкнутую цепь, условия устойчивости рассматривать не будем.
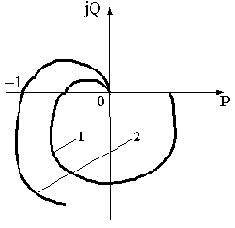
Рис.3.10
В соответствии с критерием Найквиста об устойчивости можно судить не только по АФЧХ, но и совместно по амплитудной и фазовой частотным характеристикам разомкнутой цепи. Обычно при этом пользуются логарифмическими характеристиками, что представляет большое удобство в силу простоты их построения. Но если ЛАЧХ используется асимптотическая, то расчеты будут достаточно грубыми.
Неохват АФЧХ точки (- 1, j0) имеет место, если при частоте, на которой A( )=1, абсолютное значение фазы меньше
)=1, абсолютное значение фазы меньше  .
.
Но значение А=1 соответствует G=20lgA=0.
Поэтому для устойчивости замкнутой САУ необходимо, чтобы ЛАЧХ разомкнутой цепи пересекла ось абсцисс раньше, чем фаза, спадая, окончательно перейдет за значение -  .
.
На рис.3.11 приведены ЛАЧХ и ЛФЧХ, соответствующие устойчивости некоторой САУ.
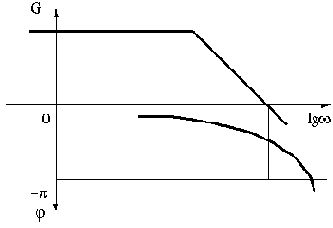
Рис.3.11
Критерий Найквиста позволяет оценить устойчивость САУ, содержащих звенья с запаздыванием.
Пусть звено с запаздыванием с передаточной функцией 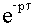 (при единичном коэффициенте передачи) включено последовательно с системой без запаздывания с передаточной функцией W0(p).
(при единичном коэффициенте передачи) включено последовательно с системой без запаздывания с передаточной функцией W0(p).
Результирующие передаточная и комплексная частотная функции разомкнутой цепи будут:
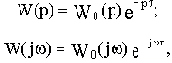
где 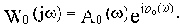
С учетом последнего
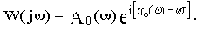
Видно, что звено с запаздыванием лишь вносит дополнительный сдвиг. При этом изменяется АФЧХ, т.е. меняются условия устойчивости (характеристика "закручивается" по часовой стрелке). При некотором  САУ станет неустойчивой.
САУ станет неустойчивой.
По АФЧХ системы без запаздывания можно определить критическое (предельное) значение запаздывания  , что поясняется построением на рис.3.12.
, что поясняется построением на рис.3.12.
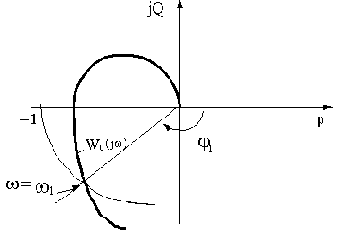
Рис.3.12
Определяется точка, для которой 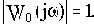 Частота, соответствующая этой точке -
Частота, соответствующая этой точке - 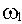 , а фаза -
, а фаза - 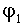 .
.
При введении запаздывания условие совпадения этой точки с точкой (- 1, j0) запишется
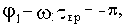
откуда
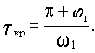
Физический смысл критерия Найквиста заключается в том, что при увеличении частоты входного воздействия сигнал, проходящий по цепи обратной связи, оказывается в противофазе с входным. А это равносильно замене отрицательной обратной связи на положительную. Если же при этой частоте разомкнутый контур обладает усилением (т.е. k>1), то замкнутая САУ становится неустойчивой (любое увеличение сигнала на выходе приводит к увеличению сигнала на входе по цепи обратной связи, что вызывает дальнейший рост выходного сигнала и т.д.).
Для аналитических расчетов с помощью критерия Найквиста условия нахождения системы на границе устойчивости можно записать в двух формах:
а) используя вещественную и мнимую частотные функции разомкнутой цепи
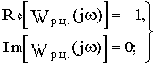 (3.8)
(3.8)
б) используя амплитудную и фазовую частотные характеристики разомкнутой цепи
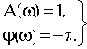 (3.9)
(3.9)
Аналитические расчеты существенно упрощаются в частном случае, когда в числителе Wр.ц.(p) присутствует только коэффициент передачи k, как, например, в структуре на рис.3.3. При этом комплексную частотную функцию можно записать
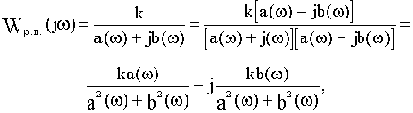
где 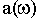 и
и 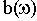 - соответственно действительная и мнимая части знаменателя
- соответственно действительная и мнимая части знаменателя 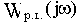 .
.
Но 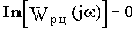 в том случае, если
в том случае, если 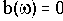 , значит
, значит

Тогда условия нахождения САУ на границе устойчивости (3.8) преобразуются к виду
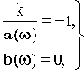 или
или 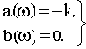 (3.10)
(3.10)
Определим, воспользовавшись условием (3.10), значение kгр для структуры на рис.3.3.
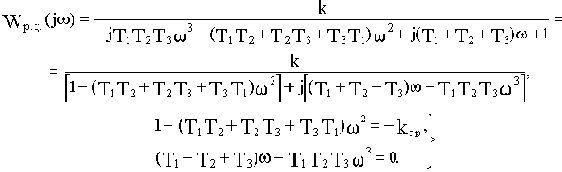
Из второго уравнения выразим 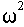 (корень
(корень  отбросим, т.к. по критерию Найквиста АФЧХ должна проходить через характерную точку при
отбросим, т.к. по критерию Найквиста АФЧХ должна проходить через характерную точку при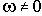 ) и подставим в первое уравнение:
) и подставим в первое уравнение:
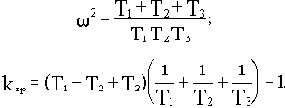
Такой же результат был получен ранее по критериям Гурвица и Михайлова.
Пример 3.5.
Решить задачу примера 3.1 с использованием критерия Найквиста.
Рассчитаем kгр, воспользовавшись условием (3.8).
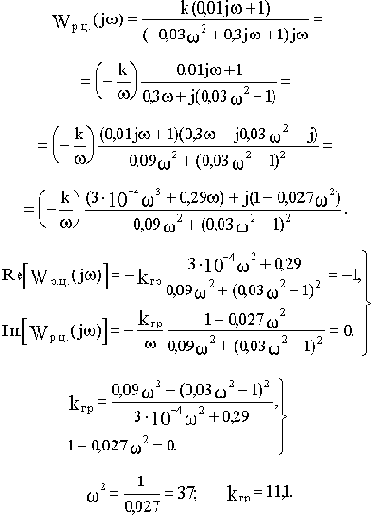
Ответ тот же, что и в примерах 3.1 и 3.2.
К содержанию
Минимально- и неминимально-фазовые звенья
Введем вначале понятия нулей и полюсов передаточной функции. Нулями передаточной функции 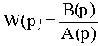 называют корни уравнения B(p)=0, т.е. такие значения р, при которых передаточная функция обращается в нуль, а полюсами - корни уравнения A(p)=0, т.е. такие значения р, при которых передаточная функция обращается в бесконечность.
называют корни уравнения B(p)=0, т.е. такие значения р, при которых передаточная функция обращается в нуль, а полюсами - корни уравнения A(p)=0, т.е. такие значения р, при которых передаточная функция обращается в бесконечность.
Звено называется минимально-фазовым, если все нули и полюса его передаточной функции имеют отрицательные или равные нулю вещественные части.
Звено называют неминимально-фазовым, если хотя бы один нуль или полюс его передаточной функции имеет положительную вещественную часть.
Все рассмотренные выше типовые звенья, кроме звена чистого запаздывания, являются минимально-фазовыми.
Возьмем в качестве примера неминимально-фазовое звено с передаточной функцией
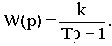
Такое звено можно получить, если охватить апериодическое звено с передаточной функцией W0(p)=k0/(T0p+1) положительной обратной связью с передаточной функцией W0c(p)=k0c Эквивалентная передаточная функция такого соединения будет
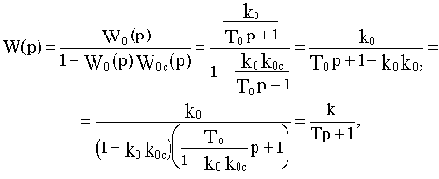
где 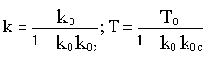
При k0k0c>1 параметры k и Т будут отрицательны, но если умножить и числитель, и знаменатель выведенной передаточной функции на минус единицу, то получим записанную выше передаточную функцию неминимально-фазового звена.
Эта передаточная функция имеет положительный полюс p1=1/T.
Частотные характеристики такого звена:
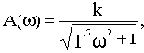
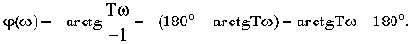
Но для обычного апериодического звена имеем:
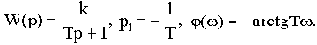
Разница между ними. как видим, в величине фазы. Амплитудные же характеристики одинаковы. Оказывается, что из всех возможных звеньев с одинаковыми амплитудными характеристиками обычные типовые звенья обладают наименьшими по абсолютному значению фазовыми характеристиками. В этом и состоит смысл введенных терминов.
Важным свойством минимально-фазовых звеньев является однозначное соответствие амплитудной и фазовой частотных характеристик. Другими словами, по заданной амплитудной характеристике можно определить фазовую и наоборот.
К содержанию
Параллельная коррекция
Параллельные корректирующие устройства реализуются в виде обратных связей. Корректирующие обратные связи (охватывающие отдельные звенья или участки цепи САУ) помимо классификации на отрицательные и положительные, делятся на жесткие и гибкие. Жесткие обратные связи осуществляются статическими звеньями 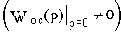 , гибкие - дифференцирующими
, гибкие - дифференцирующими 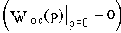 .
.
Рассмотрим действие идеальной жесткой обратной связи с передаточной функцией Woc(p)=koc
Пусть эта обратная связь охватывает апериодическое звено с передаточной функцией
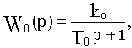
как показано на рис.4.13.
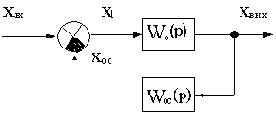
Рис.4.13
В результате охвата обратной связью получим
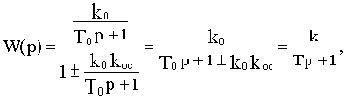
где 
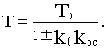
Постоянная времени и коэффициент передачи уменьшаются при отрицательной обратной связи и увеличиваются при положительной. На рис.4.14 иллюстрируется физическая суть механизма уменьшения инерционности при отрицательной обратной связи.
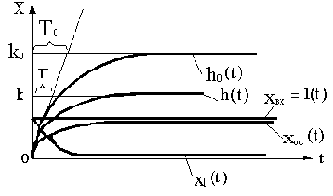
Рис.4.14
Переходная характеристика h0(t) соответствует апериодическому звену без обратной связи, а характеристика h(t)- с обратной связью.
Кривая сигнала x1(t)=1(t)-xoc(t) на входе звена имеет всплеск вначале. За счет его происходит форсировка на входе по сравнению с окончательным установившимся значением x1, которая и дает ускорение переходного процесса.
При инерционности обратной связи скорость роста xoc еще более замедлится, увеличится длительность форсировки на входе звена, в результате чего еще более повысится быстродействие.
В качестве жесткой корректирующей обратной связи применяется в основном отрицательная обратная связь для уменьшения инерционности.
Заметим попутно, что отрицательная обратная связь имеет и другие достоинства: она уменьшает остающуюся вне рассмотрения нелинейность статической характеристики звена, нестабильность его параметров во времени, а также при наличии шумов (помех) на входе или внутри звена уменьшает уровень шумов на выходе.
При охвате жесткой обратной связью интегрирующего звена с
W0(p)=k0/p имеем:
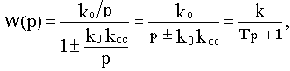
где
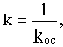
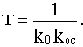
Таким образом интегрирующее звено превращается в статическое. Практический интерес при этом представляет лишь отрицательная связь (при положительной звено получается неустойчивым).
Рассмотрим далее влияние безинерционной гибкой обратной связи с Woc(p)=kocp, называемой еще гибкой обратной связью по скорости.
В общем случае для звена с передаточной функцией 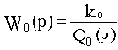 имеем:
имеем:
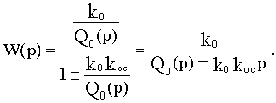
Таким образом гибкая обратная связь, не влияя на коэффициент передачи охватываемого звена, изменяет коэффициент при р в знаменателе передаточной функции.
В случае апериодического звена изменится постоянная времени (при положительной обратной связи уменьшится, а при отрицательной - возрастет), в случае колебательного - изменится коэффициент демпфирования.
К содержанию
Передаточная функция
Целью рассмотрения САУ может быть решение одной из двух задач: задачи анализа или задачи синтеза. Но в любом случае порядок исследования САУ включает в себя следующие этапы: математическое описание, исследование установившихся режимов, исследование переходных режимов.
Рассмотрим случай, когда в замкнутой системе можно выделить объект О и управляющее устройство УУ, как показано на рис.2.1.
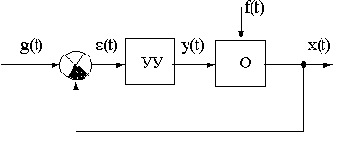
Рис.2.1
Общее уравнение САУ получается из системы уравнений объекта и управляющего устройства.
Состояние объекта характеризуется выходной величиной x(t), регулирующим воздействием y(t) и возмущением f(t). Тогда выходная величина может быть представлена функцией:
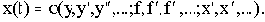
Состояние управляющего устройства характеризуется регулирующим воздействием y(t) и входным воздействием  . Процессы в УУ будут описываться двумя уравнениями:
. Процессы в УУ будут описываться двумя уравнениями:
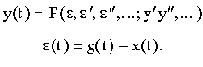
Три последних уравнения полностью описывают процессы в САУ. Если в этих уравнениях исключить переменные y(t) и  , то получим дифференциальное уравнение САУ:
, то получим дифференциальное уравнение САУ:
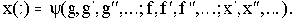
Это уравнение оценивает состояние системы во времени, определяет переходные процессы и обычно называется уравнением динамики.
Однако в форме дифференциальных уравнений математическое описание в теории автоматического управления обычно не применяется вследствие сложности решения таких уравнений.
Исследование САУ существенно упрощается при использовании прикладных математических методов операционного исчисления.
Возьмем некоторый элемент САУ, имеющий один вход и один выход. Дифференциальное уравнение элемента в общем случае имеет вид:
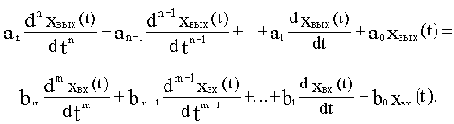
Если в уравнение (2.1) вместо функции времени xвых(t) и xвх(t) ввести функции Xвых(p) и Xвх(p) комплексного переменного р, поставив условием, что эти функции связаны зависимостями:
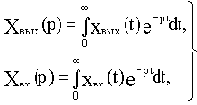 (2.2)
(2.2)
то оказывается, что дифференциальное уравнение, содержащее функции xвых(t) и xвх(t) при нулевых начальных условиях, равносильно линейному алгебраическому уравнению, содержащему функции Xвых(p) и Xвх(p):
anpnXвых(p)+an-1pn-1Xвых(p)+...+a1pXвых(p)+a0Xвых(p)=
=bmpmXвх(p)+bm-1pm-1Xвх(p)+...+b1pXвх(p)+b0Xвх(p).(2.3)
Такой переход от дифференциального уравнения к однозначно соответствующему ему алгебраическому уравнению называется преобразованием Лапласа.
Функция X(p) называется изображением функции x(t), функция x(t) называется оригиналом функции X(p).
Операция перехода от искомой функции x(t) к ее изображению X(p) (нахождение изображения от оригинала) называется прямым преобразованием Лапласа и записывается условно с помощью символа L как
L{x(t)}=X(p).
Операция перехода от изображения X(p) к искомой функции x(t) (нахождение оригинала по изображению) называется обратным преобразованием Лапласа и записывается условно с помощью символа L-1 как
L-1{X(p)}=x(t).
Формально переход от дифференциального уравнения к алгебраическому относительно изображения при нулевых начальных условиях получается путем замены символов дифференцирования оригиналов функций dn/dtn, dn-1/dtn-1...,d/dt соответственно на pn,pn-1,...p и функций x(t)- их изображениями X(p). С комплексной переменной p, как и с другими членами алгебраического уравнения, можно производить различные действия: умножение, деление, вынесение за скобки и т.д.
Так как возможность однозначного перехода от дифференциального уравнения к алгебраическому значительно упрощает расчеты, то важно убедиться в правомерности такого перехода.
Обозначим в исходном дифференциальном уравнении 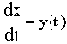 и согласно интегралу (2.2) найдем изображение:
и согласно интегралу (2.2) найдем изображение:
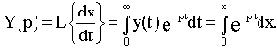
Согласно правилу интегрирования по частям
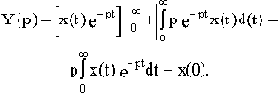
При нулевых начальных условиях x(0)=0 и с учетом (2.2) получим:
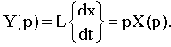
Таким образом, операция дифференцирования оригинала соответствует операции умножения изображения этого оригинала на комплексное число p.
Так как
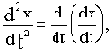 то
то 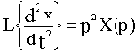 и т.д.
и т.д.
Каждый элемент САУ в общем случае описывается дифференциальным уравнением вида (2.1). Следовательно, при выводе дифференциального уравнения системы в целом необходимо совместно решить несколько дифференциальных уравнений высших порядков.
Преобразование дифференциальных уравнений по Лапласу позволяет свести эту задачу к решению системы алгебраических уравнений. Определив из алгебраических уравнений изображение X(p) искомой функции x(t), определяющей переходной процесс в системе, находят эту функцию, пользуясь таблицами оригиналов и изображений или по известным формулам обратного преобразования Лапласа.
Кроме того, преобразование дифференциального уравнения по Лапласу дает возможность ввести понятие передаточной функции.
Вынеся в уравнении (2.3) Xвых(p) и Xвх(p) за скобки, получим:
(anpn+an-1pn-1+...+a1p+a0)Xвых(p)=
=(bmpm+bm-1pm-1+...+b1p+b0)Xвх(p).
Определим из этого уравнения отношение изображения выходной величины к изображению входной:
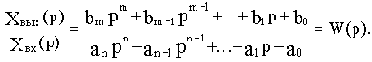 (2.4)
(2.4)
Отношение изображения выходной величины элемента (или системы) к изображению его входной величины при нулевых начальных условиях называется передаточной функцией элемента (или системы).
Передаточная функция W(p) является дробно-рациональной функцией комплексной переменной р:

где A(p)=anpn+an-1pn-1+...+a1p+a0- полином степени n,
B(p)=bmpm+bm-1pm-1+...+b1p+b0- полином степени m.
Из определения передаточной функции следует, что:
Xвых(p)=Xвх(p)W(p).
Передаточная функция является основной формой математического описания объектов в теории автоматического управления и так как она полностью определяет динамические свойства объекта, то первоначальная задача расчета САУ сводится к определению передаточной функции.
Рассмотрим примеры по определению передаточной функций некоторых простейших схем, характерных для электроники.
Пример 2.1.
Вывести передаточную функцию для схемы на рис.2.2, считая входным воздействием приложенное напряжение u, а выходным - ток в цепи i.
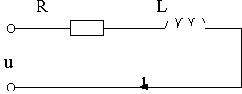
Рис.2.2
Процессы в схеме описываются уравнением:
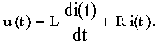
Перейдем к изображениям по Лапласу:
U(p)=LpI(p)+RI(p)=I(p)(Lp+1).
Составим передаточную функцию как отношение изображения выходной величины к изображению входной величины:
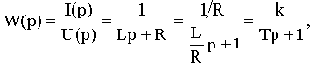
где k=1/R- коэффициент передачи,
T=L/R- постоянная времени.
Передаточные функции принято записывать в такой форме, чтобы свободные члены полиномов от р равнялись бы единице, что и сделано как в рассмотренном примере, так и в последующих.
Пример 2.2.
Вывести передаточную функцию схемы на рис.2.3, считая входной величиной напряжение u1, а выходной - u2.

Рис.2.3
При выводе передаточной функции будем считать, что цепочка не нагружена (никаких элементов к выходным зажимам не подключено, либо эти элементы имеют сопротивление, стремящееся к бесконечности) и сопротивление источника входного напряжения настолько велико, что его можно считать равным бесконечности.
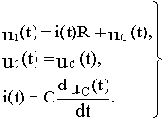
(а)
(б)
(в)
Подставим (в) в (а):
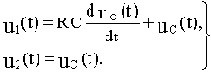
Перейдем к изображениям:
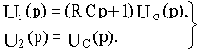
Передаточная функция
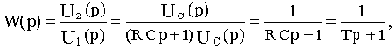
где T=RC- постоянная времени.
Пример 2.3.
Вывести передаточную функцию схемы на рис.2.4, считая входной величиной u1, выходной u2, при допущениях, сформулированных в примере 2.2. iC
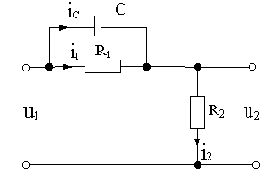
Рис.2.4
Составляем два уравнения по второму закону Кирхгофа, одно уравнение по первому закону Кирхгофа и расписываем выходную величину:
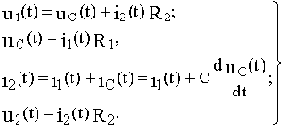
(а)
(б)
(в)
(г)
Из уравнений (б) и (в) соответственно получим:
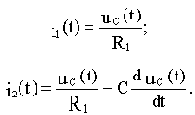
Подставим полученные выражения i1(t) и i2(t) в уравнения (а) и (г):
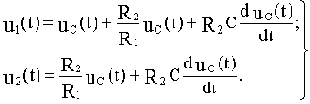
Перейдем к изображениям:
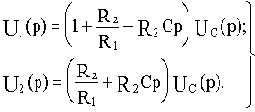
Передаточная функция:
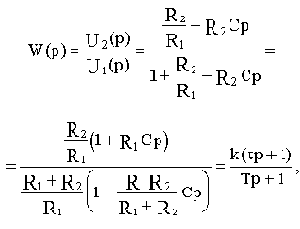
где 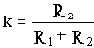 - коэффициент передачи,
- коэффициент передачи,
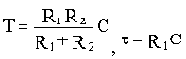 - постоянные времени.
- постоянные времени.
Пример 2.4.
Вывести передаточную функцию схемы на рис.2.5, считая входной величиной u1, выходной - u2, при допущениях, сформулированных в примере 2.2.
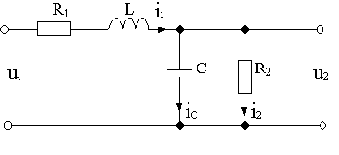
Рис.2.5
Система уравнений электрического равновесия схемы для мгновенных значений величин:
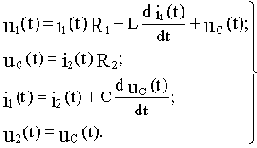
Последнее соотношение здесь, конечно, не уравнение, а обозначение выходной величины.
Уравнения в операторной форме:
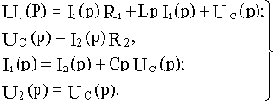
(а)
(б)
(в)
Из уравнения (б)
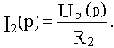
Подставим полученное значение I2(p) в (в):
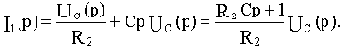
Последнее соотношение подставим в (а) и определим передаточную функцию:
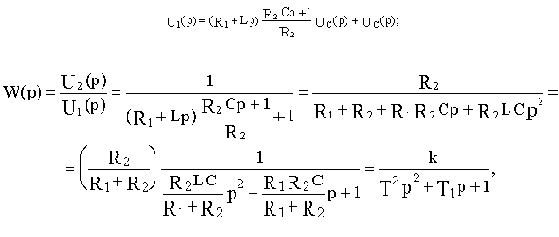
где 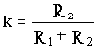 - коэффициент передачи,
- коэффициент передачи,
 - постоянные времени.
- постоянные времени.
Пример 2.5.
Вывести передаточную функцию схемы на рис.2.6, а , содержащей операционный усилитель.
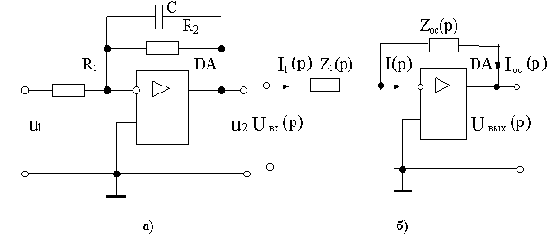
Рис.2.6
Операционными усилителями называются усилители постоянного тока малой мощности с большим коэффициентом усиления. В настоящее время они выполняются по интегральной технологии, т.е. в виде микросхем.
Выведем вначале передаточную функцию для типового включения операционного усилителя, показанного на рис.2.6, б, в общем виде.
Так как реальные микросхемы операционных усилителей имеют большой коэффициент усиления kоу и большое входное сопротивление rвх, то предположим, что 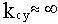 и
и 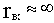 .
.
С учетом принятых допущений напряжение между инвертирующим и неинвертирующим входами операционного усилителя
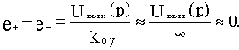
Отсюда следует, что напряжение на входе “-“ (инвертирующем)  и тогда
и тогда

Кроме того, учитывая, что 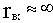 , можно считать
, можно считать 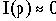 и, следовательно
и, следовательно
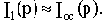
Выходное напряжение схемы тогда определяется следующим соотношением:
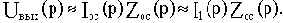
Теперь легко получить выражение для передаточной функции схемы (см.рис.2.6, б):
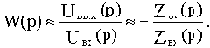 (2.5)
(2.5)
Знак “минус” в последнем выражении указывает на то, что полярность выходного напряжения схемы противоположна полярности входного напряжения.
Для определения передаточной функции схемы на рис.2.6, а вначале найдем сопротивление конденсатора ZC(p) в операторной форме.
Мгновенное значение тока через емкость равно:
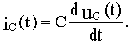
Переходя к изображениям по Лапласу:
IC(p)=CpUC(p).
Из последнего равенства
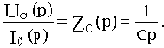
(Аналогично для индуктивности можно получить ZL(p)=Lp).
Используя выведенное значение ZC(p), для схемы на рис.2.6, а получим:
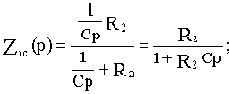 Z1(p)=R1;
Z1(p)=R1;
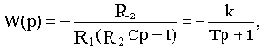
где k=R2/R1- коэффициент передачи,
T=R2C- постоянная времени.
К содержанию
Показатели качества
Как всякая динамическая система, САУ может находиться в одном из двух режимов - стационарном (установившемся) и переходном. Стационарный режим может быть двух типов: статический и динамический. Ограничимся здесь рассмотрением лишь статического режима.
В статическом режиме, при котором все внешние воздействия и параметры системы не меняются, качество управления характеризуется точностью.
Рассмотрим САУ с двумя воздействиями: задающим Xвх(p) и возмущающим F(p). Структурная схема такой САУ приведена на рис.4.1, где обозначено: 1 - участок системы от входа до точки приложения возмущения; 2 - участок системы от точки приложения возмущения до выхода с передаточной функцией WF(p); 3 - цепь обратной связи.
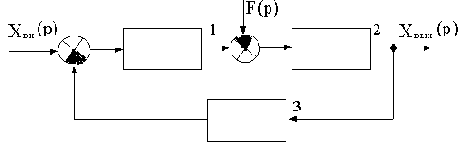
Рис.4.1
В операторной форме САУ описывается уравнением динамики:
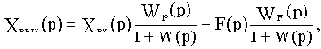
где Wp(p) - передаточная функция разомкнутой САУ,
W(p) - передаточная функция разомкнутой цепи.
Уравнение статики получается из уравнения динамики при подстановке в последнее р=0, что соответствует постоянству всех переменных, то есть равенству нулю их производных.
В рассматриваемом примере уравнение статики принимает вид:
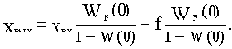
Вид W(0) и Wp(0) зависит от того, содержатся ли в системе интегрирующие звенья или нет. Рассмотрим вначале случай, когда интегрирующие звенья отсутствуют (такие САУ называются статическими).
В случае статической системы W(0)=k и WF(0)=kF так как знаменатели передаточных функций всех звеньев, входящих сомножителями в выражения W(p) и WF(p) при р=0 обращаются в единицу.
В результате получим:
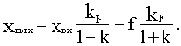 (4.1)
(4.1)
Статическая характеристика 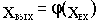 неоднозначна из-за наличия возмущения f. Статическая ошибка
неоднозначна из-за наличия возмущения f. Статическая ошибка 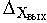 при неизменном задающем воздействии определяется выражением:
при неизменном задающем воздействии определяется выражением:
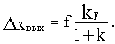
Для разомкнутой САУ уравнение статики будет иметь вид
xвых=xвхkp-fkF,
а статическая ошибка относительно замкнутой системы увеличивается в (1+k) раз:
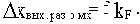
График зависимости выходной величины САУ от возмущения обычно называется внешней характеристикой, которая в общем виде представлена на рис.4.2.
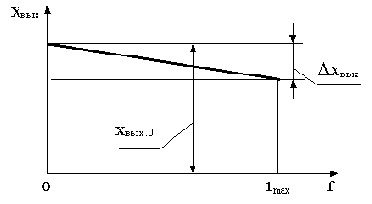
Рис.4.2
В различных областях техники точность в установившемся режиме принято характеризовать величиной отклонения выходной координаты в полном диапазоне изменения возмущающего воздействия в следующем виде:
1) абсолютной величиной отклонения. Например: 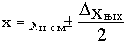 .
.
Под номинальным значением xном понимается усредненное значение выходной величины;
2) относительной величиной отклонения, выраженной в процентах. Например:
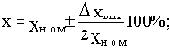 (4.2)
(4.2)
3) статизмом внешней характеристики S, определяемым выражением
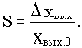
Наличие статической ошибки в общем случае является нежелательным, так как создается погрешность управления. Но для полного устранения статического отклонения требуется до бесконечности увеличивать коэффициент передачи k, что нереализуемо по ряду причин (например, по условию обеспечения устойчивости). Таким образом, в статической САУ принципиально нельзя полностью устранить статическую ошибку.
Но вместе с тем имеется путь устранения статической ошибки при конечной величине коэффициента передачи.
Введем в рассмотренную статическую САУ интегрирующее звено, причем так. чтобы оно находилось на участке 1 структурной схемы (см. рис.4.1), т.е. между точками приложения задающего и возмущающего воздействий. Теперь САУ будет описываться уравнением динамики
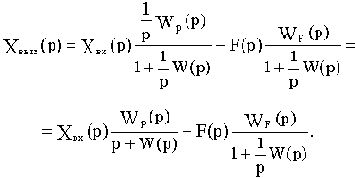
Подставив в это выражение значение р=0, получим уравнение статистики:
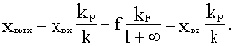
Отсюда следует, что при включении интегрирующего звена в оговоренный выше участок системы удалось полностью ликвидировать статическую ошибку, то есть получить S=0.
САУ, в которых при стремлении возмущающего воздействия к постоянной величине, отклонение выходной величины стремится к нулю и не зависит от величины приложенного воздействия, называются астатическими.
Если интегрирующее звено включить не в оговоренный выше участок структуры, а, например, в цепь обратной связи, то получим
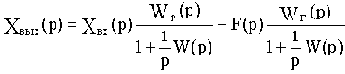
и уравнение статики
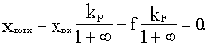
Практический смысл такая система потеряла.
В другом случае. если интегрирующее звено включить на участке 3 структуры (т.е. после точки приложения возмущения), действуя аналогично, выведем:
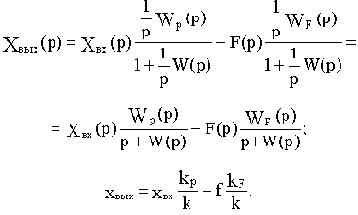
То есть система не является астатической.
Для характеристики переходного режима наибольшее распространение имеют следующие показатели качества: время переходного процесса, перерегулирование, колебательность.
Время переходного процесса
характеризует быстродействие системы. Определяется как интервал времени от начала переходного процесса до момента, когда отклонение выходной величины от ее нового установившегося значения становится меньше определенной достаточно малой величины. Обычно это пять процентов.
Перерегулированием
 называется максимальное отклонение выходной величины xmax на интервале переходного процесса от установившегося после окончания переходного процесса значения xуст, выраженное в процентах:
называется максимальное отклонение выходной величины xmax на интервале переходного процесса от установившегося после окончания переходного процесса значения xуст, выраженное в процентах:
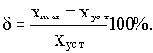
Колебательность
характеризуется обычно числом колебаний переходной характеристики за время переходного процесса. В зависимости от характера затухания различают следующие типы переходных характеристик: монотонная (нет ни одного колебания); апериодическая (не более одного колебания); колебательная (несколько колебаний).
Пример 4.1.
Рассчитать статическую точность системы стабилизации выходного напряжения генератора постоянного тока (см. рис.1.3) при следующих значениях параметров и воздействий: kу=0,5А/В; kп=10В/А; kд=0,1; rвн=0,1Ом; Uз=5В; Iн=(1...10)А.
Прежде всего необходимо составить уравнение статики рассматриваемой системы. Не зная передаточных функций отдельных элементов и системы в целом, составим математическое описание для установившегося режима на основе статических характеристик отдельных элементов (примем допущение, что все элементы имеют линейные статические характеристики).
В разомкнутой системе (см. рис.1.2), как было выведено в подразделе 1.2,
Uн=E-Iнrвн (а)
Э.д.с. генератора пропорциональна току возбуждения, т.е. Eг=Iвkп, где kп- коэффициент пропорциональности, зависящий от материала магнитопровода генератора, конструктивных особенностей генератора и т.д.
Ток возбуждения, в свою очередь, пропорционален входному сигналу усилителя У, т.е. Iв=Uзkу, где kу- коэффициент передачи функционального усилителя У.
С учетом этого соотношение (а) можно записать в следующем виде:
Uн=Uзkуkп-Iнrвн (б)
Уравнению (б) соответствует структурная схема, представленная на рис.4.3.
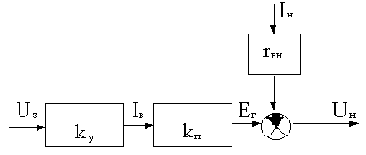
Рис.4.3
В замкнутой схеме (см. рис.1.3) часть выходного напряжения сравнивается с задающим и разность этих напряжений подается на вход усилителя У, в соответствии с чем можно записать
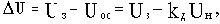 (в)
(в)
где kд=R3/(R2+R3) - коэффициент передачи делителя.
С учетом формулы (в) на основе структурной схемы разомкнутой системы составим структурную схему замкнутой системы, как показано на рис.4.4.
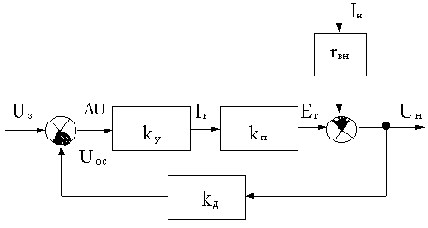
Рис.4.4
С учетом правил преобразования структурных схем для схемы на рис. 4.4 получим уравнение:
 (г)
(г)
Уравнение статики (г), как видим, полностью соответствует обобщенному уравнению (4.1), отличаясь лишь обозначениями.
Подставим в уравнение (г) заданные значения величин и определим максимальное UHmax и минимальное UHmin значение выходного напряжения, соответствующие соответственно минимальному (Iн=1 А) и максимальному (Iн=10 А) токам нагрузки:
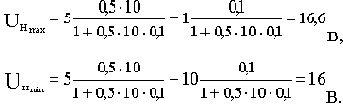
Представим выходное напряжение в форме (4.2):
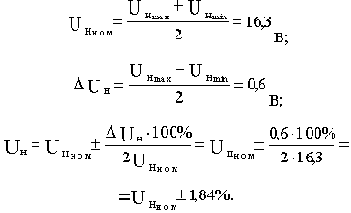
Таким образом, при изменении в оговоренномдиапазоне возмущающего воздействия (тока нагрузки) отклонение выходного напряжения не превысит величины  1,84% от номинального значения.
1,84% от номинального значения.
К содержанию
Понятие устойчивости линейных непрерывных сау
Система называется устойчивой, если:
1) после снятия воздействия по окончании переходного процесса система возвращается в исходное равновесное состояние;
2) после изменения воздействия на постоянную величину по окончании переходного процесса система приходит в новое равновестное состояние.
Определим условия устойчивости.
Выходная и входная величины в системе связаны с помощью дифференциального уравнения. Решение этого дифференциального уравнения при заданном значении входной величины представляет собой закон изменения выходной величины во времени. Но это решение состоит из двух составляющих:
x(t)=xв(t)+xсв(t),
где xв(t)- вынужденная составляющая, однозначно связанная с изменением входной величины. Она определяется как частное решение неоднородного дифференциального уравнения с правой частью;
xсв(t)- свободная составляющая, изменяющаяся во времени в течение переходного процесса.
Именно свободная составляющая и определяет переходной процесс в системе. Определяется она общим решением однородного дифференциального уравнения
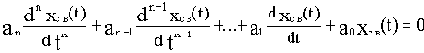
в виде суммы составляющих

где Ai- постоянные интегрирования, определяющиеся начальными условиями;
Pi- корни характеристического уравнения.
Характеристическое уравнение составляется на основании исходного дифференциального уравнения:
anpn+an-1pn-1+...+a1p+a0=0
В общем случае корни являются комплексными. При этом они образуют пары сопряженных корней:
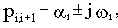
где  может быть положительной или отрицательной величиной.
может быть положительной или отрицательной величиной.
При этом, если 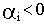 , эта составляющая будет затухать. Наоборот, при
, эта составляющая будет затухать. Наоборот, при 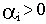 получатся расходящиеся колебания.
получатся расходящиеся колебания.
Отсюда следует, что общим условием затухания всех составляющих, а значит, и всего переходного процесса в целом является отрицательность действительных частей всех корней характеристического уравнения системы.
Если хотя бы один корень имеет положительную действительную часть, он даст расходящуюся составляющую переходного процесса и система будет неустойчивой.
Изображая корни характеристического уравнения системы точками на комплексной плоскости, как показано на рис.3.1, условие устойчивости можно сформулировать еще так: условием устойчивости САУ является расположение всех корней характеристического уравнения в левой комплексной полуплоскости.
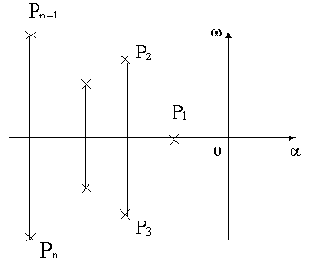
Рис.3.1
Мнимая ось  плоскости корней служит границей устойчивости. При этом можно выделить три случая выхода САУ на границу устойчивости, которые характеризуются соответственно:
плоскости корней служит границей устойчивости. При этом можно выделить три случая выхода САУ на границу устойчивости, которые характеризуются соответственно:
1) нулевым корнем p1=0;
2) парой чисто мнимых корней 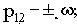
3) бесконечно удаленным корнем 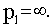
Бесконечность на комплексной плоскости рассматривается как бесконечно удаленная точка, противоположная нулевой. Поэтому она тоже является границей между правой и левой полуплоскостями.
Вычисление корней весьма просто лишь для характеристического уравнения первой и второй степени. Но ведь для определения устойчивости не нужно знать абсолютное значение корней, необходимо знать лишь, в какой полуплоскости они находятся. Поэтому важное значение приобретают правила, позволяющие определять устойчивость системы без вычисления корней. Эти правила называют критериями устойчивости.
К основным критериям устойчивости относятся алгебраический критерий Гурвица и частотные критерии Михайлова и Найквиста.
К содержанию
Понятие запаса устойчивости
При оценке устойчивости САУ одного факта устойчивости недостаточно. Необходимо еще оценить величину запаса устойчивости, т.е. степени удаленности системы от границы устойчивости.
Основное распространение в качестве меры запаса устойчивости получили вытекающие из критерия Найквиста две величины - запас устойчивости по фазе 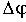 и запас устойчивости по амплитуде
и запас устойчивости по амплитуде 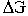 , которые показаны на рис.3.13.
, которые показаны на рис.3.13.
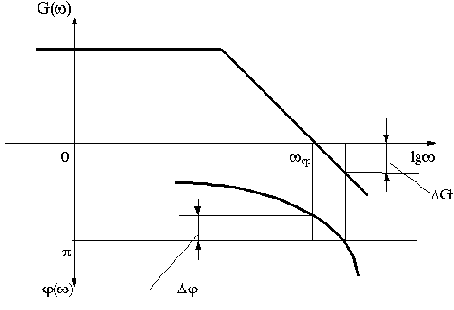
Рис.3.13
Запас устойчивости по фазе
определяется величиной 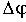 , на которую должно возрасти запаздывание по фазе в системе с частотой среза
, на которую должно возрасти запаздывание по фазе в системе с частотой среза , чтобы система оказалась на границе устойчивости.
, чтобы система оказалась на границе устойчивости.
Запас устойчивости по амплитуде
определяется величиной 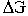 допустимого подъема ЛАЧХ, при котором система окажется на границе устойчивости. Таким образом, запас по амплитуде представляет собой запас по коэффициенту передачи разомкнутой цепи по отношению к его граничному по устойчивости значению:
допустимого подъема ЛАЧХ, при котором система окажется на границе устойчивости. Таким образом, запас по амплитуде представляет собой запас по коэффициенту передачи разомкнутой цепи по отношению к его граничному по устойчивости значению:
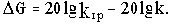 (3.11)
(3.11)
Для вычисления запаса устойчивости по амплитуде необходимо по любому из критериев устойчивости определить kгр и воспользоваться далее формулой (3.11).
При вычислении запаса устойчивости по фазе нужно вначале определить частоту среза из уравнения 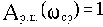 и затем найти
и затем найти 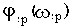 . Запас устойчивости по фазе будет равен
. Запас устойчивости по фазе будет равен
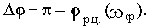 (3.12)
(3.12)
При наличии частотных характеристик запасы устойчивости отсчитываются прямо с графиков, например, как показано на рис. 3.13. Помими логарифмических характеристик, с этой же целью можно использовать и АФЧХ (разомкнутой цепи), что проиллюстрировано на рис.3.14.
Для определения запаса устойчивости по фазе нужно провести луч из начала координат через точку АФЧХ, для которой выполняется условие 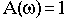 . Для нахождения этой точки графически следует из начала координат провести окружность радиусом R=1. Угол между этим лучем и отрицательной действительной полуосью и будет
. Для нахождения этой точки графически следует из начала координат провести окружность радиусом R=1. Угол между этим лучем и отрицательной действительной полуосью и будет 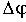 .
.
Запас устойчивости по амплитуде характеризует удаленность точки АФЧХ 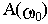 от границы устойчивости, т.е. от точки с координатами - 1, j0 (
от границы устойчивости, т.е. от точки с координатами - 1, j0 (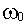 - это частота, при которой фаза составляет значение минус
- это частота, при которой фаза составляет значение минус  ), выражение в логарифмических единицах. Следовательно,
), выражение в логарифмических единицах. Следовательно, 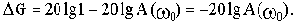
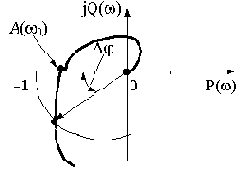
Рис.3.14
К содержанию
Последовательная коррекция динамических свойств
Коррекция динамических свойств осуществляется с целью выполнения требований по устойчивости и качеству переходного процесса.
Осуществляется коррекция с помощью введения в САУ специальных корректирующих звеньев. Эти звенья могут включаться либо последовательно с основными звеньями САУ, либо параллельно им. Соответственно они и называются: последовательные либо параллельные корректирующие звенья.
Последовательные корректирующие звенья можно разделить на три типа: пропорционально-дифференцирующие (ПД), пропорционально-интегрирующие (ПИ) и пропорционально-интегро-дифференцирующие (ПИД) звенья.
ПД-звено имеет передаточную функцию
WПД(p)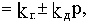
то есть выходная величина этого звена пропорциональна входной величине и ее первой производной.
Включение этого звена в САУ приводит к тому, что передаточная функция разомкнутого контура САУ
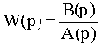
умножается на WПД(p), то есть принимает вид
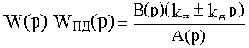
В результате характеристический полином замкнутой САУ D(р) будет следующий:
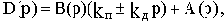
где A(p)=anpn+an-1pn-1+...+a1p+a0.
Положим, что В(р)=k (так как мы исследуем влияние ПД-звена, то логично предположить, что в исходной САУ такого звена не было, но тогда числитель передаточной функции исходной САУ содержит лишь величину k). Тогда можно видеть, что в характеристическом полиноме замкнутой САУ изменится коэффициент при р в первой степени. Включение двух ПД-звеньев приведет к изменению коэффициента и при p2 и т.д. Изменение же этих коэффициентов изменяет условия устойчивости и качество переходного процесса.
Рассмотрим в качестве примера применение данного звена для стабилизации, то есть обеспечения устойчивости САУ с астатизмом выше первого порядка (порядок астатизма - это число интегрирующих звеньев в приведенной одноконтурной САУ).
Передаточную функцию разомкнутой САУ с порядком астатизма, равным r, можно представить в виде:
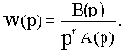
Соответственно характеристический полином замкнутой САУ будет:
D(р)=В(р)+prA(p).
Если В(р)=k, то из последнего выражения следует вывод о том, что САУ с порядком астатизма r>1 являются структурно неустойчивыми, поскольку в D(р) отсутствуют члены с р в степени от единицы до (r-1) (по критерию устойчивости Гурвица).
Введем теперь в систему (r-1) ПД-звеньев. При этом в харктеристическом полиноме появятся недостающие звенья:
D(p)=k(kп+kД1p+...+kД(r-1)pr-1)+prA(p).
Следовательно, САУ становится структурно устойчивой.
Влияние ПД-звена на качество переходного процесса продемонстрируем на примере последовательного соединения этого звена с апериодическим звеном с передаточной функцией

Передаточная функция последовательного соединения этих звеньев:

Соответственно переходная функция
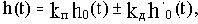
где h0(t)- переходная функция апериодического звена.
Из последнего выражения видно, что отрицательное дополнительное воздействие по производной снижает быстродействие, а положительное, наоборот, повышает его. Например, при kд/kп=T0 полностью компенсируется инерционность апериодического звена:
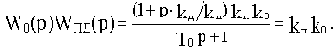
Реальные ПД-звенья обладают инерционностью, то есть имеют следующую передаточную функцию:

где 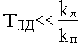
Все сказанное выше об идеальном ПД-звене справедливо и для реального с той только разницей, что реальное слабее влияет на быстродействие и на области устойчивости.
ЛАЧХ реального ПД-звена приведена на рис.4.10.
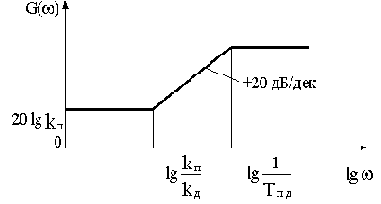
Рис.4.10
ПД-звено является фильтром верхних частот, так как его ЛАЧХ растет с увеличением частоты. Поэтому введение этого звена в САУ расширяет ее полосу пропускания, повышает быстродействие.
Практически наиболее просто ПД-звенья реализуются в электрических системах постоянного тока, где они представляют собой пассивные RC- и RL- цепочки. Один из возможных вариантов представлен на рис.2.4.
Пример реализации ПД-звена на операционном усилителе приведен на рис.4.11.
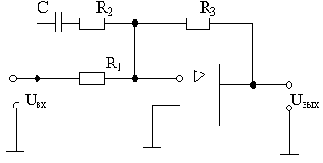
Рис.4.11

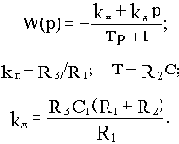
Пропорционально-интегрирующее (ПИ) звено имеет передаточную функцию
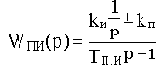
В случае ТПИ=0 получаем идеальное ПИ-звено.
Последнее выражение можно представить так:
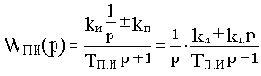
Таким образом, ПИ-звено эквивалентно последовательному соединению интегрирующего звена и ПД-звена. По своим частотным свойствам ПИ-звено противоположно ПД-звену, являясь фильтром нижних частот. ЛАЧХ ПИ-звена приведена на рис.4.12.
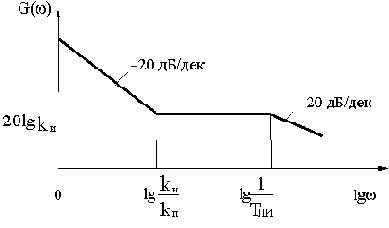
Рис. 4.12
Передаточная функция пропорционально-интегро-дифференциру-ющего (ПИД) звена
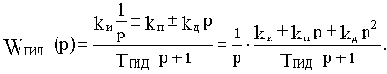
Это звено эквивалентно последовательному соединению интегрирующего звена и пропорционально-дифференцирующего с воздействием по двум производным или, что то же самое, последовательному соединению ПИ-звена и ПД-звена с одной производной. Таким образом, ПИД-звено повышает порядок астатизма, как и ПИ-звено, но при этом одновременно дает более сильную коррекцию динамических свойств САУ.
Такое звено подчеркивает как нижние, так и средние частоты, подавляя средние, как видно из приближенной ЛАЧХ ПИД-звена, приведенной на рис.4.12.
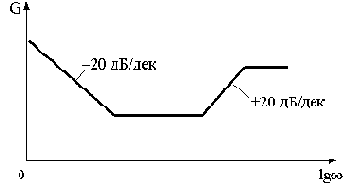
Рис.4.12
В связи с видом ЛАЧХ ПИД-звеньями называют не только звенья с указанной выше передаточной функцией Wпид(p), но и любые другие звенья, ЛАЧХ которых имеет минимум на средних частотах и растет в сторону как низких, так и высоких частот.
Вообще указанные выше наименования типов последовательных корректирующих звеньев в значительной степени условны прежде всего из-за инерционности реальных корректирующих звеньев.
Наиболее просто синтез последовательного корректирующего устройства можно произвести по ЛАЧХ. Для этого необходимо использовать ЛАЧХ нескорректированной САУ Gнескорр( ) и желаемую ЛАЧХ, Gскорр(
) и желаемую ЛАЧХ, Gскорр( ) соответствующую заданному переходному процессу. ЛАЧХ Gскорр(
) соответствующую заданному переходному процессу. ЛАЧХ Gскорр( ) получают с помощью частотного критерия качества, иллюстрированного приведенными выше графиками (см. рис.4.7, рис.4.8).
) получают с помощью частотного критерия качества, иллюстрированного приведенными выше графиками (см. рис.4.7, рис.4.8).
При последовательном соединении звеньев справедливо соотношение
Wскорр(р)= Wнескорр(р)Wку(р),
где Wку(р) - передаточная функция синтезируемого последовательного корректирующего устройства.
Следовательно
Wку(р)=Wскорр(р)/Wнескорр(р).
Перейдем к частотной форме записи, используя логарифмические единицы:
20lg |Wку(р)( )|=20lg |Wcкорр.(
)|=20lg |Wcкорр.( )|- 20lg |Wнескорр.(
)|- 20lg |Wнескорр.( )|;
)|;
Gку( )=Gскорр.(
)=Gскорр.( ) - Gнескорр.(
) - Gнескорр.( ).
).
Тип и параметры последовательного корректирующего устройства получают следующим образом:
1) графически вычитают из желаемой ЛАЧХ ординаты ЛАЧХ исходной системы;
2) упрощают ЛАЧХ корректирующего устройства, сравнивают с ЛАЧХ имеющихся в справочных данных типовых корректирующих звеньев и выбирают конкретную схему корректирующего звена;
3) находят по сопрягающим частотам параметры схемы корректирующего устройства.
К содержанию
Предмет дисциплины и историческая справка
Прежде всего, если речь идет об управлении, то имеется объект управления, т.е. некий механизм, агрегат или устройство, некий технологический, энергетический или транспортный процесс, желаемое поведение или протекание которого должно быть обеспечено.
Поведение объекта управления, результат его действия определяется некоторыми показателями. Чаще всего ими являются значения каких-то физических величин, которые называют выходными величинами или выходными координатами объекта управления.
В реальных условиях на каждое устройство или процесс многочисленные воздействия оказывает внешняя среда. Все воздействия, с точки зрения их влияния на действие объекта, на его выходные величины, разделяются на две принципиально отличительные группы. Некоторые из воздействий обеспечивают желаемое изменение поведения объекта, достижение поставленных целей. Такие воздействия называют управляющими, при их отсутствии задача управления вообще не имеет решения.
Другие воздействия, напротив, мешают достижению цели, и изменить их, как правило, невозможно. Такие воздействия называют возмущающими (или просто возмущениями).
Задача управления, по существу, заключается в формировании такого закона изменения управляющих воздействий, при котором достигается желаемое поведение объекта независимо от наличия возмущений.
Сложная и разностороння задача управления включает более узкую задачу регулирования, которую главным образом и будем рассматривать в дальнейшем. Задача регулирования заключается в поддержании выходных величин объекта равными (или пропорциональными) некоторым эталонным функциям времени - задающим воздействиям. Последние могут быть постоянными или изменяющимися как по заданному, так и по заранее неизвестному закону.
Объект управления может принадлежать как к неживой природе, в частности, быть техническим устройством, так и к живой природе (коллектив людей). В свою очередь, само управление также может осуществляться как человеком (пилот управляет самолетом), так и техническим устройством (самолетом управляет автопилот).
Первые публикации исследований в этой области начинаются с 30-х годов прошлого века (первая известная публикация Д.С. Чижова была в 1823 г.). Наиболее важными, признанными фундаментальными, явились три теоретические работы, содержащие основы новой науки. Это работы Д.К. Максвелла "О регуляторах" (1866) и работы И.А. Вышнеградского "Об общей теории регуляторов" (1876) и "О регуляторах прямого действия" (1877). Д.К. Максвелл и И.А. Вышнеградский рассмотрели машину (т.е. объект) и регулятор как единую динамическую систему, обосновали общий методологический подход к исследованию самых разнородных по физике и конструкции систем, заложили основы теории устойчивости, установили ряд важных общих закономерностей регулирования по принципу обратной связи.
Крупный вклад в теорию регулирования внесен Н.Е. Жуковским, автором труда "О прочности движения" и первого учебника "Теория регулирования хода машин" (1909).
В первые десятилетия XX в. теория автоматического управления, вышедшая из рамок прикладной механики, формируется как общетехническая дисциплина. В этот период появляется целый ряд работ, рассматривающих приложение теории и распространяющих ее выводы на самые разнообразные технические процессы: на регулирование электрических машин и систем; двигателей внутреннего сгорания; тепловых и паросиловых устройств; турбин; различных производственных процессов. В 1932 г. появляется работа Х. Найквиста, в которой предлагается критерий устойчивости радиотехнических усилителей с обратной связью.
Исключительно интенсивным и многогранным было развитие теории автоматического управления в послевоенный период. Это обусловлено в первую очередь развитием военной и космической техники, бурным прогрессом вычислительной техники и электроники.
В настоящее время буквально все окружающие нас технические устройства содержат в своем составе то или иное число автоматических регуляторов. Ограничиваясь для примера бытовой электроникой, перечислим лишь некоторые характерные термины: автоматическая регулировка усиления; автоподстройка частоты; стабилизация напряжения и т.д.
Системы автоматического управления (САУ) различной физической природы и совершенно различного функционального назначения могут иметь одинаковое математическое описание, то есть описываться одинаковыми уравнениями (отличаться будут лишь размерности величин). Но в САУ с одинаковым математическим описанием и процессы при управлении будут протекать одинаково, хотя действовать в них будут различные физические величины. Какие процессы могут происходить при управлении?
Во-первых, в результате приложения конечного по величине воздействия САУ должна перейти из одного равновесного состояния в другое (в противном случае она будет неустойчивой).
Во-вторых, переход из одного состояния в новое осуществляется за некоторое определенное время, на протяжении которого величина (или величины), характеризующая состояние САУ, изменяется по какому-либо закону.
В-третьих, переход САУ в новое равновесное состояние осуществляется с какой-либо точностью.
Эти вопросы, а также влияние на процесс управления отдельных параметров САУ и изучаются в настоящей дисциплине.
Причем необходимо отметить, что составление математического описания отдельных элементов или систем в целом может быть произведено лишь на основе четкого понимания физических процессов, протекающих в этих объектах и алгоритмах их функционирования. Поэтому задача получения исходного математического описания относится к предмету специальных дисциплин, в которых эти элементы изучаются.
В теории автоматического управления указанные выше вопросы изучения САУ решаются с помощью специальных методов с использованием математического описания. Отсюда следует, что возможность успешного освоения настоящей дисциплины основывается, в первую очередь, на знании высшей математики и, с учетом профиля специальности "Промышленная электроника", основ теории цепей.
К содержанию
Рекомендуемая литература
5.1. Попов Е.П. Теория линейных систем автоматического регулирования и управления. - М. Наука, 1989. - 304 с.
5.2. Теория автоматического управления. Ч.1. Теория линейных систем автоматического управления/ Н.А. Бабаков и др.; Под ред. А.А. Воронова. - М.: Высшая школа, 1986. - 367 с.
5.3. Бабаков Н.А. и др. Теория автоматического управления. Ч.1/Под ред. А.А. Воронова. - М.: Высшая школа, 1977. - 303 с.
5.4. Юревич Е.И. Теория автоматического управления. - М.: Энергия, 1975. - 416 с.
5.5. Бесекерский В.А. и др. Сборник задач по теории автоматического регулирования и управления. - М.: Наука, 1978. - 512 с.
К содержанию
Соединения некоторых типовых звеньев
Некоторые элементарные физически реализуемые объекты математически описываются как последовательное соединение нескольких типовых динамических звеньев, в том числе и идеальных.
Например, схема на рис.2.4 представляет из себя последовательное соединение идеального форсирующего и апериодического звеньев.
Построим асимптотическую ЛАЧХ для этой схемы при R1=R2=1 кОм, С=1 мкФ.
Параметры передаточной функции:
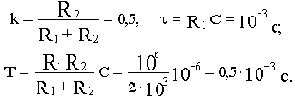
Параметры асимптотической ЛАЧХ:
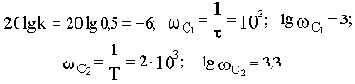
По рассчитанным параметрам строим ЛАЧХ, как показано на рис.2.20.
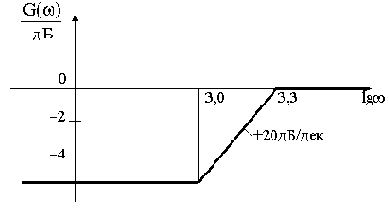
Рис.2.20
Другой аналогичный пример - схема на рис.2.21.
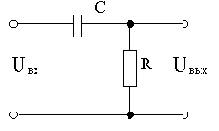
Рис.2.21
Выведем для приведенной схемы передаточную функцию:
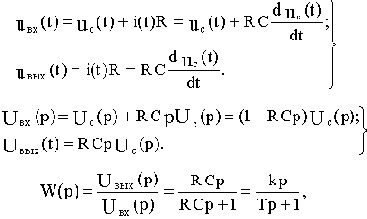
где k=T=RC.
Из полученной передаточной функции можно видеть, что рассматриваемая схема представляет из себя последовательное соединение идеального дифференцирующего и апериодического звеньев.
Построим асимптотическую ЛАЧХ для этой схемы при R=1 кОм, С=1 мкФ.
Параметры передаточной функции:
k=T=RC=10-3c.
Параметры асимптотической ЛАЧХ:
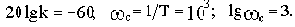
При построении ЛАЧХ откладываем точку с координатами  и проводим через нее прямую с наклоном плюс 20 дБ/дек до сопрягающей частоты. После сопрягающей частоты наклон ЛАЧХ изменяется на минус 20дБ/дек, т.е. вторая асимптота идет горизонтально. Характеристика представлена на рис.2.22.
и проводим через нее прямую с наклоном плюс 20 дБ/дек до сопрягающей частоты. После сопрягающей частоты наклон ЛАЧХ изменяется на минус 20дБ/дек, т.е. вторая асимптота идет горизонтально. Характеристика представлена на рис.2.22.
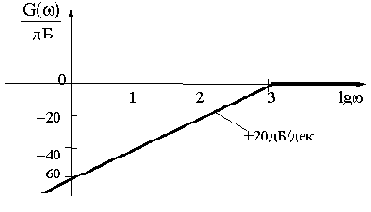
Рис.2.22
Рассмотренные здесь схемы зачастую называют инерционным форсирующим и инерционным дифференцирующим звеньями (или реальными форсирующим и дифференцирующим звеньями).
К содержанию
Структурные схемы и их преобразование
В теории автоматического управления под структурной схемой понимается графическое изображение математического описания. То есть для составления структурной схемы система дробится на элементы, каждый из которых описывается простейшим математическим выражением ( в виде передаточной функции). Структурные схемы содержат следующие четыре типа элементов: звенья направленного действия; устройства сравнения, или сумматоры; линии связи; точки разветвления (узлы).
Звенья направленного действия изображаются прямоугольниками, внутри которых записываются их передаточные функции.
Между собой звенья соединяются с помощью линий связи. На этих линиях стрелками указывается направление распространения сигналов. Следует подчеркнуть, что в направлениях, противоположных указанным стрелками, сигналы не распространяются. Сами линии связи, также как и сумматоры, считаются идеальными, то есть никакими параметрами не обладают.
Сумматоры предназначены для суммирования сигналов (с учетом знака сигнала), как и на функциональных схемах.
Для распределения сигналов по различным направлениям используются узлы, которые обозначаются точками в местах пересечения линий связи.
Для удобства расчетов бывает необходимо преобразовать исходную структурную схему системы к какому-либо желаемому виду, чаще всего - к цепи последовательно соединенных звеньев. В связи с этим рассмотрим основные правила преобразования структурных схем.
При последовательном соединении n звеньев с передаточными функциями Wi(p) эквивалентная передаточная функция Wэ(p) определяется их произведением:
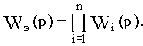
При параллельном соединении n звеньев эквивалентная передаточная функция определяется суммой передаточных функций Wi(p) отдельных звеньев:
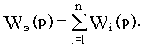
Для случая обратной связи при выводе эквивалентной передаточной функции замкнутого участка Wз(p) используем обозначения, приведенные на рис.2.8.
Схема замкнутого участка системы
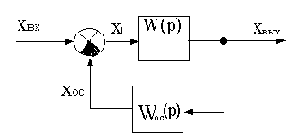
Рис.2.8
Обратная связь называется отрицательной, если
x1=xвх-xoc,
как показано на схеме, и положительно, если
x1=xвх+xoc.
В случае отрицательной обратной связи в изображениях по Лапласу с учетом указанных направлений распространения сигналов запишем:
Xвых(p)=X1(p)W1(p)=[Xвх(p)-Xoc(p)]W(p)=
[Xвх(p)-Xвых(p)Woc(p)]W(p).
Отсюда получаем передаточную функцию
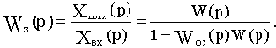
Для положительной обратной связи в знаменателе формулы знак "плюс" меняется на "минус".
Указанные три вида преобразования структурных схем являются наиболее часто встречающимися. Для остальных случаев сформулируем основной принцип преобразования и поясним несколькими примерами. При преобразовании структурной схемы передача сигнала по выбранному направлению не должна меняться.
Например, в структурной схеме на рис.2.9, а необходимо перенести узел через звено с передаточной функцией W2(p).
Преобразование структурной схемы
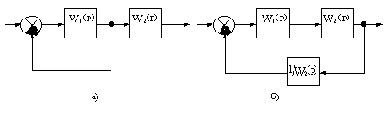
Рис.2.9
Чтобы передача сигнала по цепи обратной связи не изменилась, необходимо ввести фиктивное звено с передаточной функцией 1/W2(p), как показано на рис.2.9, б.
В более сложных случаях в процессе преобразования необходимо производить определенные расчеты.
Например, в схеме на рис.2.10, а узел 1 необходимо перенести на выход звена с передаточной функцией W2(p).
Преобразование структурной схемы
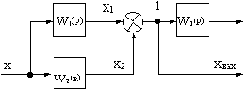
а)
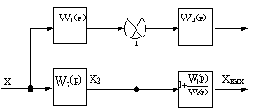
б)
Рис.2.10
Установим связь между величинами Xвых(p) и X2(p).
На входе звеньев с передаточными функциями W1(p) и W2(p) действует сигнал
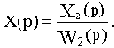
На выходе звена с передаточной функцией W1(p)
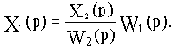
На выходе сумматора в узле 1
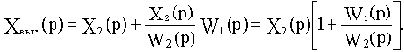
Отсюда видно, что в рассматриваемом примере при переносе узла необходимо ввести фиктивное звено с передаточной функцией 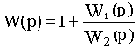 , как показано на рис. 2.10, б.
, как показано на рис. 2.10, б.
При переносе узла в схеме на рис.2.11, а с выхода сумматора на его положительный вход найдем передаточную функцию фиктивного звена без дополнительных пояснений.
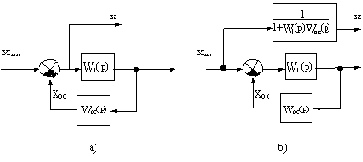
Рис.2.11
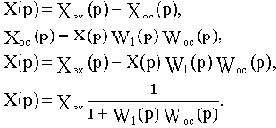
К содержанию
Типовые звенья и их характеристики
В общем случае какой-либо объект в теории автоматического управления описывается передаточной функцией, содержащей полиномы от р произвольного порядка в числителе и знаменателе. Но если передаточная функция объекта содержит только простой множитель в числителе (знаменатель при этом представляет собой действительное число) либо только простой множитель в знаменателе (числитель представляет собой действительное число), то объект называется типовым динамическим звеном (или просто типовым звеном).
Из курса алгебры известно, что полином любого порядка можно разложить на простые множители. То есть любую САУ можно представить в виде последовательного соединения типовых звеньев. С другой стороны, реальные звенья САУ могут иметь самую разнообразную физическую основу (электронные, механические, гидравлические, электромеханические и т.п.) и конструктивное выполнение, но иметь одинаковые передаточные функции и являться одинаковыми типовыми звеньями. Поэтому знание характеристик звеньев столь же необходимо для расчетов САУ, как знание таблицы умножения в арифметике.
Все линейные типовые звенья разделяют на три группы: позиционные звенья, интегрирующие и дифференцирующие. Позиционные звенья: апериодическое, пропорциональное, колебательное, консервативное и чистого запаздывания - характеризуется тем, что в каждом из них, кроме консервативного, при подаче на вход постоянной величины с течением времени устанавливается постоянное значение выходной величины.
В звеньях, относящихся к группе интегрирующих, при постоянном входном воздействии выходная величина неограниченно растет.
Дифференцирующие звенья характеризуются тем, что реагируют только на изменение входной величины.
Рассмотрим типовые звенья и их характеристики.
Пропорциональное (безинерционное) звено
. Описывается уравнением и имеет передаточную функцию:
xвых(t)=kxвх(t),W(p)=k.
Параметр k называется в общем случае коэффициентом передачи звена и может иметь любую размерность. В частных случаях, когда k является величиной безразмерной, принято пользоваться термином "коэффициент усиления".
Частные и временные функции звена:
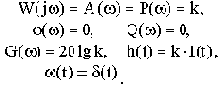
Примерами таких звеньев могут служить механические связи, электронные усилители сигналов на низких частотах и др.
Схема на рис.2.6, б, если Z1(p)=R1 и Zoc(p)=Roc, также будет являться пропорциональным звеном.
Интегрирующее (идеальное) звено.
Уравнение и передаточная функция звена:
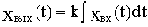 или
или 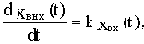
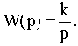
В случае интегрирующего звена параметр k является коэффициентом передачи звена по скорости, численно равным скорости изменения выходной величины при единичном значении входной величины.
Частотные и временные функции звена:
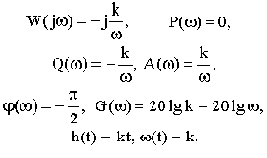
Построенные по указанным функциям характеристики звена представлены на рис.2.12.
При построении ЛАЧХ удобно отложить точку с координатами 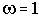 (при этом
(при этом 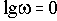 );
); 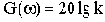 и провести прямую с наклоном минус 20 дБ/дек, так как с увеличением частоты на одну декаду ордината ЛАЧХ уменьшается на 20 дБ. (При каком-то значении
и провести прямую с наклоном минус 20 дБ/дек, так как с увеличением частоты на одну декаду ордината ЛАЧХ уменьшается на 20 дБ. (При каком-то значении 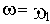 получаем
получаем 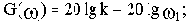 при увеличении частоты на одну декаду, т.е. при
при увеличении частоты на одну декаду, т.е. при 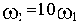 , соответственно
, соответственно 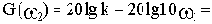
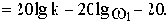 Разность этих ординат
Разность этих ординат 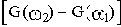 составляет минус 20 дБ).
составляет минус 20 дБ).
В качестве примера элемента, характеристики которого приближенно соответствуют характеристикам идеального интегрирующего звена, можно назвать двигатель постоянного тока с независимым возбуждением и малой электромеханической инерцией. Входной величиной для него является напряжение на зажимах якоря, а выходной - угол поворота вала.
Схема на рис.2.6, б будет являться интегрирующим звеном, если Z1(p)=R1, а цепь обратной связи организована конденсатором, т.е. 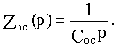
На самом деле, согласно формуле (2.5) передаточная функция схемы будет

где k=1/T=1/(R1Coc).
При использовании в рассматриваемой схеме реального операционного усилителя переходная характеристика не может иметь значения, превышающие напряжение питания . Но если предположить операционный усилитель идеальным, то и реализованное здесь интегрирующее звено будет идеальным.
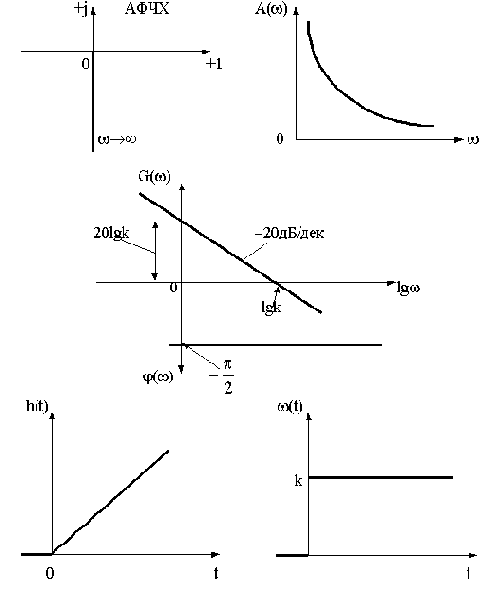
Рис.2.12
Дифференцирующее (идеальное) звено.
Уравнение и передаточная функции звена:
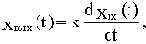 W(p)=kp.
W(p)=kp.
Выходная величина пропорциональна скорости изменения входной величины.
Если входная и выходная величины имеют одинаковую размерность, то коэффициент k измеряется в секундах. В этом случае его принято обозначать через Т и называть постоянной времени дифференцирующего звена.
Выражение для основных функций:
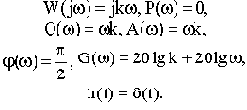
Как передаточная функция, так соответственно и частотные характеристики дифференцирующего звена обратны передаточной функции и соответствующим характеристикам интегрирующего звена.
О том, что звено с представленным математическим описанием является идеальным, говорит, к примеру, переходная функция. Ни в каком реальном устройстве невозможно получить скачек выходной величины бесконечной амплитуды.
Реальные дифференцирующие звенья обладают конечной инерционностью, вследствии чего осуществляемое ими дифференцирование не является точным. Примером может служить тахогенератор, если за его входную величину принять угол поворота его вала, а за выходную величину - выходное напряжение. Последнее пропорционально угловой скорости вращения вала, которая в свою очередь равна производной от угла поворота.
Логарифмические частотные характеристики рассматриваемого звена приведены на рис.2.13.
При построении ЛАЧХ удобно отложить точку с координатами 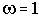 (при этом
(при этом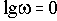 );
); 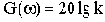 и провести через нее прямую с наклоном плюс 20 дБ/дек, так как с увеличением частоты на одну декаду ордината ЛАЧХ увеличивается на 20 дБ.
и провести через нее прямую с наклоном плюс 20 дБ/дек, так как с увеличением частоты на одну декаду ордината ЛАЧХ увеличивается на 20 дБ.
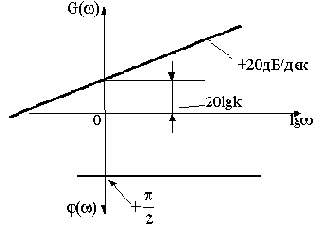
Рис.2.13
Апериодическое (первого порядка) звено.
Описывается дифференциальным уравнением
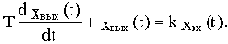
Перейдя к изображениям, получим:
TpXвых(p)+Xвых(p)=kXвх(p)
Передаточные и частотные функции:
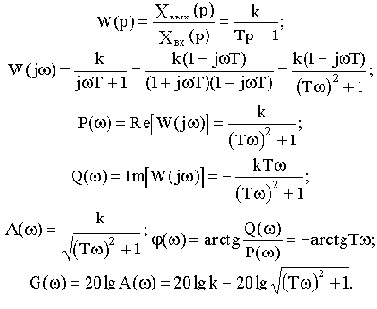
ЛАЧХ звена показана на рис.2.14. Но эта же характеристика может быть представлена приближенно ломаной линией, которая показана на том же рисунке. Эта приближенная характеристика называется асимптотической ЛАЧХ. Такое название связано с тем, что эта характеристика составлена из двух асимптот, к которым стремится ЛАЧХ при  и
и  .
.
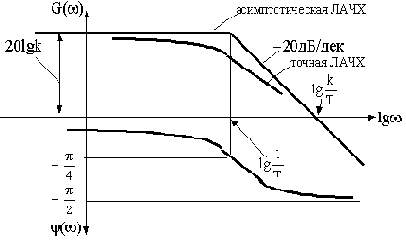
Рис.2.14
При малых значениях  можно считать
можно считать 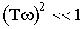 , то есть
, то есть  , следовательно
, следовательно 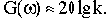
Соответственно характеристика представляет собой прямую, параллельную оси абсцисс и проходящую на уровне 20lgk. Это есть первая асимптота, к которой стремится ЛАЧХ при .
.
С другой стороны, на больших частотах
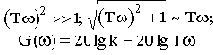
В этом случае характеристика представляет собой прямую, имеющую наклон минус 20 дБ/дек. Действительно, при увеличении  на декаду, т.е. в 10 раз,
на декаду, т.е. в 10 раз,
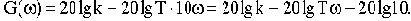
Таким образом, величина 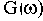 уменьшилась на 20lg10, т.е. на 20 дБ. Эта линия является асимптотой, к которой стремится ЛАЧХ при
уменьшилась на 20lg10, т.е. на 20 дБ. Эта линия является асимптотой, к которой стремится ЛАЧХ при  . Обе асимптоты пересекаются в точке, соответствующей частоте
. Обе асимптоты пересекаются в точке, соответствующей частоте 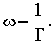 Поэтому эта частота называется сопрягающей частотой.
Поэтому эта частота называется сопрягающей частотой.
Максимальное расхождение между точной (GТ) и асимптотической (Ga) ЛАЧХ наблюдается при частоте, равной сопрягающей.
Вычислим это расхождение, подставив в соотношения для GT и Ga значения сопрягающей частоты 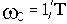 :
:
 дБ.
дБ.
От параметров звена рассматриваемая величина не зависит.
На этом же рисунке показана и ЛФЧХ: при  значение
значение  изменяется от 0 до минус
изменяется от 0 до минус  . При этом в точке
. При этом в точке 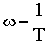 имеем
имеем 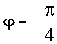 .
.
АФЧХ представляет собой полуокружность с радиусом  в четвертом квадранте комплексной плоскости и центром в точке (
в четвертом квадранте комплексной плоскости и центром в точке ( , j0) на действительной оси.
, j0) на действительной оси.
Переходная функция, согласно решению уравнения звена, при xвх=1(t) и нулевых начальных условиях имеет вид

а импульсная переходная функция
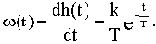
Переходная характеристика представлена на рис.2.15.
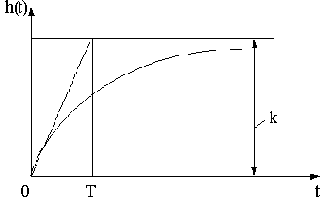
Рис.2.15
Динамические свойства звена характеризуются постоянной времени Т. Постоянная времени может быть определена как время, в течение которого выходная величина достигла бы своего нового установившегося значения, если бы она изменялась с постоянной скоростью, равной скорости изменения ее в начальный момент времени.
Коэффициент передачи k определяет свойства звена в установившемся режиме.
Очевидно, имея в распоряжении частотные либо переходные характеристики, полученные, например, экспериментально, можно восстановить передаточную функцию звена.
В рассмотренных выше примерах по определению передаточных функций схемы на рис.2.2; рис.2.3; рис.2.6, а являются апериодическими звеньями.
Пример 2.6.
Асимптотическая ЛАЧХ апериодического звена имеет частоту среза 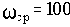 . Коэффициент передачи звена k=10. Требуется определить постоянную времени Т.
. Коэффициент передачи звена k=10. Требуется определить постоянную времени Т.
Нужно на графике или мысленно провести из точки на оси частот 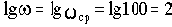 прямую с наклоном минус 20 дБ/дек до пересечения с горизонталью, проведенной на уровне
прямую с наклоном минус 20 дБ/дек до пересечения с горизонталью, проведенной на уровне 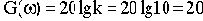 . Координата точки пересечения по оси частот даст логарифм сопрягающей частоты
. Координата точки пересечения по оси частот даст логарифм сопрягающей частоты 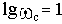 , отсюда
, отсюда 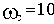 и
и 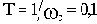 с.
с.
Звенья второго порядка.
В общем случае описываются уравнением
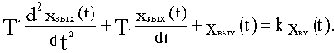
Перейдем к изображениям по Лапласу:
(T2p2+T1p+1)Xвых(p)=kXвх(p).
Отсюда определяем передаточную функцию:
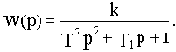
Однако общепринята запись передаточной функции звеньев второго порядка в другом виде:

где 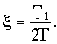
Звенья второго порядка, таким образом, характеризуются тремя параметрами. Это коэффициент передачи. постоянная времени и коэффициент демпфирования  . В зависимости от величины коэффициента демпфирования различают типы звеньев: колебательное (0<
. В зависимости от величины коэффициента демпфирования различают типы звеньев: колебательное (0< <1), консервативное (
<1), консервативное ( =0) и апериодическое второго порядка (
=0) и апериодическое второго порядка ( ).
).
Рассмотрим свойства колебательного звена. Выражения для его частотных функций имеют следующий вид:
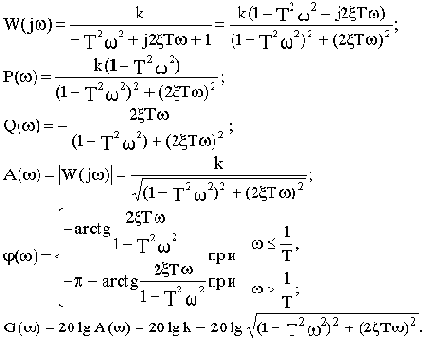
Асимптотическая ЛАЧХ строится тем же приемом, что и для апериодического звена. В области низких частот  <<1и в подкоренном выражении всеми членами. кроме 1, можно пренебречь. Тогда низкочастотная асимптота G(
<<1и в подкоренном выражении всеми членами. кроме 1, можно пренебречь. Тогда низкочастотная асимптота G( )нч принимает вид
)нч принимает вид
G( )нч 20lgk.
)нч 20lgk.
В области высоких частот 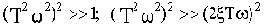 и в подкоренном выражении можно оставить лишь
и в подкоренном выражении можно оставить лишь  , пренебрегая остальными членами. Высокочастотная асимптота G(
, пренебрегая остальными членами. Высокочастотная асимптота G( )вч описывается формулой:
)вч описывается формулой:
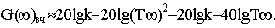
Эта асимптота имеет наклон минус 40 дБ/дек. Сопрягаются асимптоты на частоте 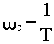 , как показано на рис.2.16.
, как показано на рис.2.16.
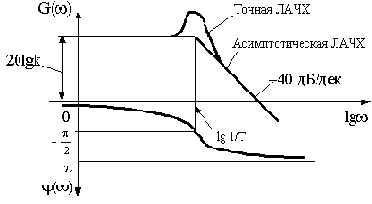
Рис.2.16
Точная ЛАЧХ GT несколько отличается от асимптотической Ga. Максимальная ошибка - в районе около сопрягающей частоты. Для упрощенных расчетов можно считать, что наибольшая ошибка будет при 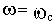 :
:
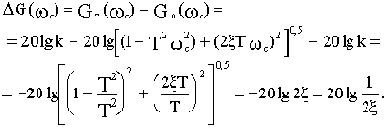
В районе  точная ЛАЧХ идет ниже асимптотической при
точная ЛАЧХ идет ниже асимптотической при 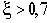 и выше - при
и выше - при 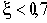 . При значениях
. При значениях  ошибка становится существенной (более трех децибел) и ее необходимо учитывать, используя приведенную выше формулу либо поправочные кривые из справочной литературы.
ошибка становится существенной (более трех децибел) и ее необходимо учитывать, используя приведенную выше формулу либо поправочные кривые из справочной литературы.
Представление о динамических свойствах звена можно получить из переходной характеристики, представленной на рис.2.17.

Рис.2.17
Примером звена второго порядка может служить колебательный контур (см. схему на рис.2.5 и вывод передаточной функции в примере 2.4).
Консервативное звено - частный случай колебательного звена, когда отсутствует демпфирование. Если обратиться к приведенному выше примеру (см. рис.2.5), то должны отсутствовать потери в контуре (выполняться условие R=0). В этом случае колебания стали бы незатухающими и переходная характеристика описывалась бы выражением:
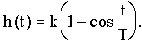
На сопрягающей частоте ЛАЧХ консервативного звена имеет всплеск бесконечной амплитуды, т.е. претерпевает разрыв, а ЛФЧХ из нулевого значения скачком достигает значения минус  .
.
При  передаточную функцию звена второго порядка можно преобразовать следующим образом:
передаточную функцию звена второго порядка можно преобразовать следующим образом:
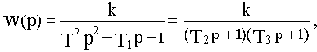
где 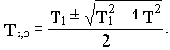
То есть апериодическое звено второго порядка не является типовым или элементарным, так как его можно представить двумя последовательно соединенными более простыми звеньями - апериодическими первого порядка.
Пример 2.7.
Определить, при каком соотношении параметров элементов схемы колебательный контур (см. рис.2.5) является колебательным звеном.
Запишем полученную в примере 2.4 передаточную функцию с использованием коэффициента демпфирования:
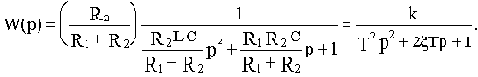
Отсюда выразим коэффициент демпфирования:
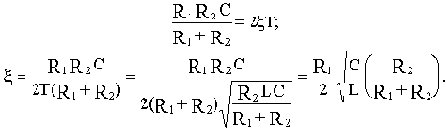
Звено будет колебательным, если  <1, т.е.
<1, т.е.
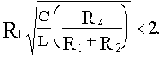
В противном случае, т.е. при
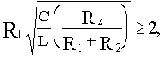
контур будет являться апериодическим звеном второго порядка. При этом следует обратить внимание на то, что лишь с позиций математического описания схему можно представить как последовательное соединение двух апериодических звеньев первого порядка. Расчленить же принципиальную схему на два участка, каждый из которых был бы соответствующим апериодическим звеном первого порядка, невозможно.
Звено чистого запаздывания.
Это звено без искажения воспроизводит на выходе входную величину, как идеальное пропорциональное звено, но с той разницей, что выходная величина запаздывает относительно входной на постоянное время. Уравнение такого звена имеет вид:
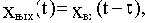
где  - время запаздывания.
- время запаздывания.
Очевидно, характеристики этого звена будут:
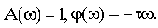
Отсюда АФЧХ:
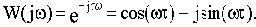
Передаточная функция:

В качестве примера звена можно назвать длинную электрическую линию без потерь, механический транспортер и т.д.
По существу это звено относится к нелинейным. Однако при расчетах САУ с такими звеньями можно применять методы теории линейных систем. Поэтому часто элементы, закон движения которых мало изучен или трудно представим в аналитической форме, после некоторой идеализации представляются в виде звеньев запаздывания.
К содержанию
Временные функции и характеристики
Под временными характеристиками в общем случае понимается графическое изображение процесса изменения выходной величины в функции времени при переходе системы из одного равновесного состояния в другое в результате поступления на вход системы некоторого типового воздействия.
Так как дифференциальное уравнение системы тоже определяет изменение выходной величины в функции времени при некоторых начальных условиях, то временная характеристика изображает собой решение дифференциального уравнения для принятого типового воздействия и, следовательно. полностью характеризует динамические свойства системы.
Так как временные характеристики могут быть получены не только путем решения дифференциального уравнения, но и экспериментально, то возможность определения динамических свойств системы по временной характеристике имеет исключительно важное практическое значение, поскольку в этом случае не требуется выводить и решать дифференциальное уравнение.
В качестве типовых воздействий наиболее широкое применение находят единичное ступенчатое и единичное импульсное воздействия.
Математическое выражение единичного ступенчатого воздействия может быть записано в виде

Под единичным импульсным воздействием понимается предельно короткий импульс
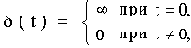
площадь которого равна единице, то есть

Выражение для единичного импульса  в математике принято называть дельта-функцией.
в математике принято называть дельта-функцией.
Графическое изображение реакции системы на единичное ступенчатое воздействие называется переходной характеристикой.
Аналитическое выражение переходной характеристики обозначается h(t) и называется переходной функцией.
Графическое изображение реакции системы на единичное импульсное воздействие называется импульсной переходной характеристикой.
Аналитическое выражение импульсной переходной характеристики обозначается  и называется импульсной переходной функцией или весовой функцией (функцией веса).
и называется импульсной переходной функцией или весовой функцией (функцией веса).
При практических расчетах наиболее широкое применение находит временная характеристика в виде переходной характеристики, так как ее достаточно просто получить экспериментально и, кроме того, определяемый ею переходный процесс часто возникает при включениях и изменениях задающего воздействия.
При поступлении на вход системы с передаточной функцией W(p) величины xвх(t)=1(t) на выходе получаем переходную характеристику xвых(t)=h(t).
В преобразованном по Лапласу виде входная и выходная величины запишутся
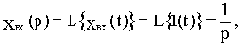
L{h(t)}=h(p)=xвых(p).
С учетом этих соотношений получим:
 (2.9)
(2.9)
Из последнего выражения следует, что по переходной функции можно получить передаточную функцию.
При поступлении на вход САР величины 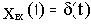 на выходе получаем импульсную переходную характеристику
на выходе получаем импульсную переходную характеристику  или в преобразованном по Лапласу виде:
или в преобразованном по Лапласу виде:
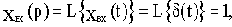
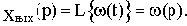
В результате определим:
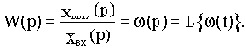 (2.10)
(2.10)
Установим связь между переходной и импульсной переходной функциями, приравняв правые части выражений (2.9) и (2.10):

Но так как р соответствует символу дифференцирования, то

Импульсная переходная функция является производной от переходной функции.
К содержанию
�
 Учет: Делопроизводство - Автоматизация - Софт
Учет: Делопроизводство - Автоматизация - Софт
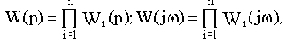
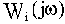 - передаточные и комплексные частотные функ-
- передаточные и комплексные частотные функ-
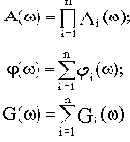
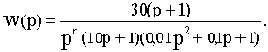
 , а в каждом простом множителе в числителе и знаменателе передаточной функции присутствует Tp):
, а в каждом простом множителе в числителе и знаменателе передаточной функции присутствует Tp):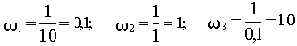
 - сопрягающая частота апериодического звена,
- сопрягающая частота апериодического звена, - сопрягающая частота форсирующего звена,
- сопрягающая частота форсирующего звена, - сопрягающая частота колебательного звена.
- сопрягающая частота колебательного звена.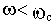 совпадают с осью частот.
совпадают с осью частот.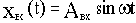 , то после затухания переходных процессов на выходе также возникают синусоидальные колебания
, то после затухания переходных процессов на выходе также возникают синусоидальные колебания 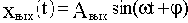 с той же частотой, но с другой амплитудой и сдвинутые по фазе относительно входных колебаний. Как известно из курса "Основы теории цепей, часть 1", синусоидально изменяющиеся величины удобно изображать с помощью комплексных амплитуд. Комплексные амплитуды рассматриваемых здесь входных и выходных колебаний можно записать как
с той же частотой, но с другой амплитудой и сдвинутые по фазе относительно входных колебаний. Как известно из курса "Основы теории цепей, часть 1", синусоидально изменяющиеся величины удобно изображать с помощью комплексных амплитуд. Комплексные амплитуды рассматриваемых здесь входных и выходных колебаний можно записать как 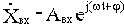 и
и 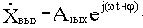
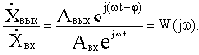 (2.6)
(2.6)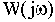 называется комплексной частотной и получается чисто формально, без каких-либо вычислений, путем замены в выражении передаточной функции переменной р на переменную
называется комплексной частотной и получается чисто формально, без каких-либо вычислений, путем замены в выражении передаточной функции переменной р на переменную  :
: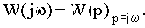 (2.7)
(2.7)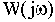 можно представить в следующем виде:
можно представить в следующем виде: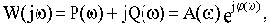 (2.8)
(2.8)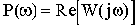 и
и 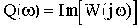 - действительная и мнимая части комплексной частотной функции,
- действительная и мнимая части комплексной частотной функции, и
и  - модуль и аргумент комплексной частотной функции.
- модуль и аргумент комплексной частотной функции. комплексную частотную функцию можно изобразить вектором на комплексной плоскости, как показано на рис.2.7.
комплексную частотную функцию можно изобразить вектором на комплексной плоскости, как показано на рис.2.7.
 называется вещественной частотной, а
называется вещественной частотной, а  - мнимой частотной характеристикой.
- мнимой частотной характеристикой. показывает отношение амплитуд выходного и входного гармонических сигналов при изменении частоты и называется амплитудной частотной характеристикой.
показывает отношение амплитуд выходного и входного гармонических сигналов при изменении частоты и называется амплитудной частотной характеристикой. показывает сдвиг фазы выходного гармонического сигнала относительно входного при изменении частоты и называется фазовой частотной характеристикой.
показывает сдвиг фазы выходного гармонического сигнала относительно входного при изменении частоты и называется фазовой частотной характеристикой.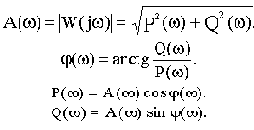
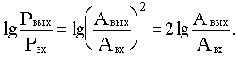
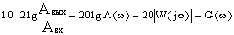
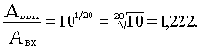
 , построенная в полулогарифмическом масштабе (в координатах: угол
, построенная в полулогарифмическом масштабе (в координатах: угол  в градусах или радианах и
в градусах или радианах и  ), называется логарифмической фазовой частотной характеристикой (ЛФЧХ).
), называется логарифмической фазовой частотной характеристикой (ЛФЧХ).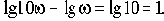
 , так как
, так как  . Поэтому начало координат можно брать в любой удобной точке в зависимости от интересующего диапазона частот.
. Поэтому начало координат можно брать в любой удобной точке в зависимости от интересующего диапазона частот. . Ось абсцисс соответствует значению
. Ось абсцисс соответствует значению 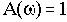 , то есть прохождению амплитуды сигнала в натуральную величину (поэтому еще говорят, что на частоте среза система теряет усилительные свойства).
, то есть прохождению амплитуды сигнала в натуральную величину (поэтому еще говорят, что на частоте среза система теряет усилительные свойства). и фазовую Woc(p). Из этих двух экспериментальных остальные частотные характеристики могут быть рассчитаны по соответствующим формулам, например
и фазовую Woc(p). Из этих двух экспериментальных остальные частотные характеристики могут быть рассчитаны по соответствующим формулам, например 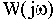 - по формуле (2.8). Кроме того, рассчитав по экспериментальным данным
- по формуле (2.8). Кроме того, рассчитав по экспериментальным данным 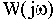 , по (2.7) путем обратной подстановки (заменив
, по (2.7) путем обратной подстановки (заменив  на р) можно получить передаточную функцию, по (2.4) - из передаточной функции дифференциальное уравнение в операторной форме и далее, применив обратное преобразование Лапласа - дифференциальное уравнение (уравнение динамики системы).
на р) можно получить передаточную функцию, по (2.4) - из передаточной функции дифференциальное уравнение в операторной форме и далее, применив обратное преобразование Лапласа - дифференциальное уравнение (уравнение динамики системы).
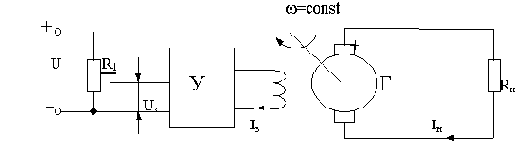
 , генератор работает на линейном участке кривой намагничивания, функциональный усилитель У обеспечивает линейную зависимость тока возбуждения Iв от задающего напряжения Uз.
, генератор работает на линейном участке кривой намагничивания, функциональный усилитель У обеспечивает линейную зависимость тока возбуждения Iв от задающего напряжения Uз. , то изменение выходного напряжения
, то изменение выходного напряжения  при этом составит величину (при условии, что Uз=const)
при этом составит величину (при условии, что Uз=const) 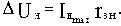
 относительно Е является величиной существенной, т.е. изменение нагрузки при неизменном задающем воздействии значительно влияет на выходное напряжение.
относительно Е является величиной существенной, т.е. изменение нагрузки при неизменном задающем воздействии значительно влияет на выходное напряжение.
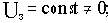
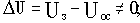 Rн=const; Iн=const; Uн=const.
Rн=const; Iн=const; Uн=const. (Uз осталось неизменным), пропорционально уменьшится Iв, уменьшится Е, уменьшится и выходное напряжение Uн. Указанные процессы будут происходить не мгновенно, а за какое-то конечное время, по истечении которого выходное напряжение с какой-то точностью вернется к исходному значению. Если бы произошло не уменьшение, а увеличение тока нагрузки, то все величины изменялись бы в противоположную сторону.
(Uз осталось неизменным), пропорционально уменьшится Iв, уменьшится Е, уменьшится и выходное напряжение Uн. Указанные процессы будут происходить не мгновенно, а за какое-то конечное время, по истечении которого выходное напряжение с какой-то точностью вернется к исходному значению. Если бы произошло не уменьшение, а увеличение тока нагрузки, то все величины изменялись бы в противоположную сторону.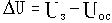 , таким образом увеличится
, таким образом увеличится , увеличатся Iв и Е, следовательно еще больше увеличится Uн. Таким образом, вызванное на начальном этапе после возмущения увеличение Uн приводит к увеличению
, увеличатся Iв и Е, следовательно еще больше увеличится Uн. Таким образом, вызванное на начальном этапе после возмущения увеличение Uн приводит к увеличению , которое в свою очередь увеличивает Uн и т.д. Схема стала неработоспособной (в первом случае обратная связь была отрицательной, во втором - положительной).
, которое в свою очередь увеличивает Uн и т.д. Схема стала неработоспособной (в первом случае обратная связь была отрицательной, во втором - положительной).
 ).
).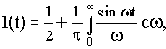
 и амплитудой
и амплитудой  при изменении
при изменении  от 0 до
от 0 до  .
.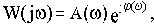
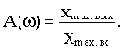
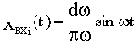 будет соответствовать колебание на выходе [с амплитудой
будет соответствовать колебание на выходе [с амплитудой 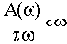 , сдвинутое по фазе относительно входного колебания на угол
, сдвинутое по фазе относительно входного колебания на угол  (
( ) ]
) ]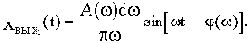
 на входе будет соответствовать постоянная составляющая
на входе будет соответствовать постоянная составляющая 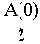 на выходе.
на выходе.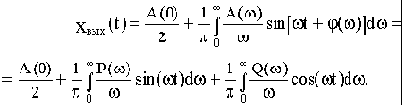 (4.3)
(4.3)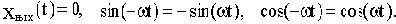
 (4.4)
(4.4)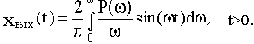 (4.5)
(4.5)
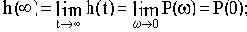

 18%;
18%;
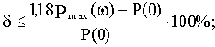
 cщ (в этом интервале Р(
cщ (в этом интервале Р( )
)  0,05 Р(0), причем
0,05 Р(0), причем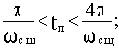
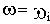 свидетельствует о медленно затухающих колебаниях с чатотой, близкой к
свидетельствует о медленно затухающих колебаниях с чатотой, близкой к 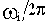 ;
; ), примерный вид которой представлен на рис.4.6.
), примерный вид которой представлен на рис.4.6.
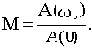
 - незатухающие колебания. Оптимальным обычно считается М=1,3-1,5. При этом переходная характеристика имеет слабую колебательность с частотой, близкой к
- незатухающие колебания. Оптимальным обычно считается М=1,3-1,5. При этом переходная характеристика имеет слабую колебательность с частотой, близкой к  .
. наклон ЛАЧХ должен составлять минус 20 дБ/дек, а значение
наклон ЛАЧХ должен составлять минус 20 дБ/дек, а значение  определяется временем переходного процесса tп и перерегулированием
определяется временем переходного процесса tп и перерегулированием  :
:
 .
. , как показано на рис.4.8, рассчитываются по выражениям:
, как показано на рис.4.8, рассчитываются по выражениям:

 и справа от
и справа от  на качество переходного процесса почти не влияют.
на качество переходного процесса почти не влияют.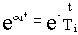 ,
,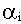 - действительная часть i-го корня характеристического уравне-
- действительная часть i-го корня характеристического уравне-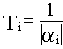 - постоянная времени затухания.
- постоянная времени затухания.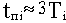 , то есть длительность составляющих переходного процесса обратно пропорциональна абсолютному значению действительной части корней характеристического уравнения.
, то есть длительность составляющих переходного процесса обратно пропорциональна абсолютному значению действительной части корней характеристического уравнения.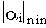 называется степенью устойчивости и обозначается
называется степенью устойчивости и обозначается 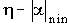 .
.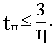
 - есть расстояние от мнимой оси, являющейся границей устойчивости, до ближайшего корня (см. рис.3.1).
- есть расстояние от мнимой оси, являющейся границей устойчивости, до ближайшего корня (см. рис.3.1).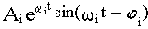 определяется отношением соседних максимумов:
определяется отношением соседних максимумов: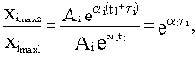
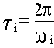 - период колебаний данной составляющей.
- период колебаний данной составляющей.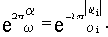
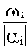 : чем оно больше, тем больше колебательность составляющей. Наиболее колебательной является составляющая, у которой это отношение максимально. Соответствующая величина обозначается
: чем оно больше, тем больше колебательность составляющей. Наиболее колебательной является составляющая, у которой это отношение максимально. Соответствующая величина обозначается 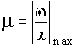 и называется степенью колебательности.
и называется степенью колебательности.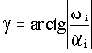 между лучом, направленным через корень из начала координат, и действительной отрицательной полуосью.
между лучом, направленным через корень из начала координат, и действительной отрицательной полуосью.
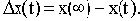
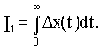
 ), будут иметь разные знаки. Поэтому по минимуму величины I1 наилучшим оказался бы процесс с незатухающими колебаниями.
), будут иметь разные знаки. Поэтому по минимуму величины I1 наилучшим оказался бы процесс с незатухающими колебаниями.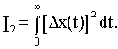

 систем третьего и четвертого порядка.
систем третьего и четвертого порядка.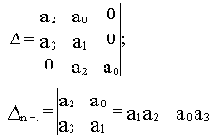 (3.1)
(3.1) (3.2)
(3.2)
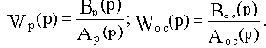
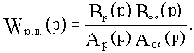
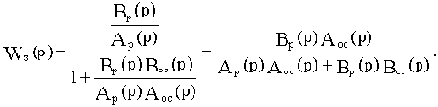

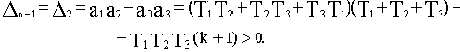
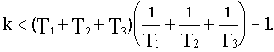
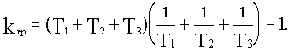 (3.5)
(3.5)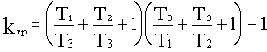
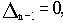 an=0, a0=0
an=0, a0=0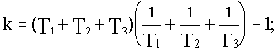


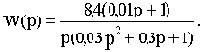
 . Получим комплексную функцию
. Получим комплексную функцию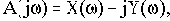
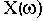 - действительная часть, полученная из членов А(р), содержащих четные степени р;
- действительная часть, полученная из членов А(р), содержащих четные степени р; - мнимая часть, полученная из членов А(р) с нечетными степенями р.
- мнимая часть, полученная из членов А(р) с нечетными степенями р. ) в виде графика в комплексной плоскости, как показано на рис.3.6.
) в виде графика в комплексной плоскости, как показано на рис.3.6.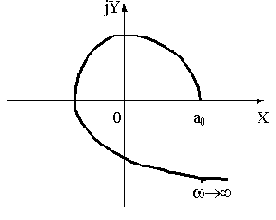
 соответствуют определенные значения Х(
соответствуют определенные значения Х( ) и Y(
) и Y( ) и определенная точка на плоскости. При
) и определенная точка на плоскости. При  =0 функция А(
=0 функция А( )=а0, т.е. годограф начинается на действительной оси. При
)=а0, т.е. годограф начинается на действительной оси. При  функция А(
функция А( ) тоже неограниченно возрастает.
) тоже неограниченно возрастает. ), начинаясь на действительной положительной полуоси, огибает против часовой стрелки начало координат, проходя последовательно n квадрантов, где n - порядок системы.
), начинаясь на действительной положительной полуоси, огибает против часовой стрелки начало координат, проходя последовательно n квадрантов, где n - порядок системы. ).
). )=0 значения частот, соответствующих точкам пересечения годографа А(
)=0 значения частот, соответствующих точкам пересечения годографа А( ) с мнимой осью, подставляют их в выражение Y(
) с мнимой осью, подставляют их в выражение Y( ). В результате получают соответствующие координаты. Аналогично находят точки пресечения А(
). В результате получают соответствующие координаты. Аналогично находят точки пресечения А( ) с действительной осью, приравнивая нулю мнимую часть Y(
) с действительной осью, приравнивая нулю мнимую часть Y( ).
). , при которых годограф А(
, при которых годограф А( ) пересекает оси координат, то есть нули Х(
) пересекает оси координат, то есть нули Х( ) и Y(
) и Y( ), нет необходимости строить сам годограф.
), нет необходимости строить сам годограф. ) и Y(
) и Y( ) чередуются с ростом
) чередуются с ростом  , начиная с
, начиная с  =0, когда Y(
=0, когда Y( )=0, а Х(
)=0, а Х( )>0.
)>0.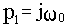 , то удовлетворяется равенство
, то удовлетворяется равенство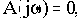
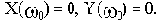
 . Физический смысл величины
. Физический смысл величины 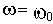 - частота колебаний системы на границе устойчивости).
- частота колебаний системы на границе устойчивости).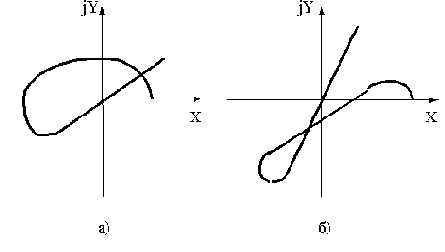
 :
: 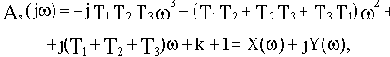
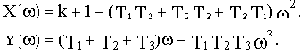
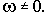 Поэтому при k=kгр:
Поэтому при k=kгр: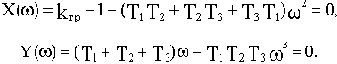
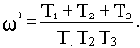
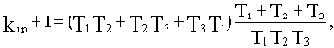
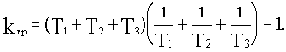
 и
и  , согласно этому критерию, имеют вид:
, согласно этому критерию, имеют вид: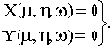
 , можно получить уравнение границы устойчивости, связывающее входящие в выражения
, можно получить уравнение границы устойчивости, связывающее входящие в выражения 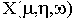 и
и 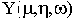 варьируемые параметры
варьируемые параметры  и
и  . Для определенности такой метод определения границы устойчивости будем называть “по критерию Михайлова”.
. Для определенности такой метод определения границы устойчивости будем называть “по критерию Михайлова”. как параметр, который изменяют от 0 до
как параметр, который изменяют от 0 до  . Каждому значению
. Каждому значению  при этом соответствует определенная точка границы устойчивости. Этот метод получения границы устойчивости принято называть методом D - разбиения.
при этом соответствует определенная точка границы устойчивости. Этот метод получения границы устойчивости принято называть методом D - разбиения.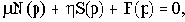
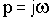 получим:
получим: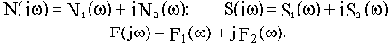
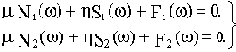 (3.6)
(3.6)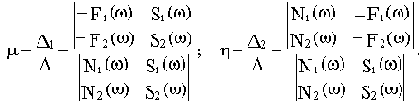 (3.7)
(3.7) ,
, ). При движении по кривой D - разбиения в сторону возрастания
). При движении по кривой D - разбиения в сторону возрастания  штриховку наносят слева, если определитель
штриховку наносят слева, если определитель  положителен, и справа - если отрицателен.
положителен, и справа - если отрицателен. :
: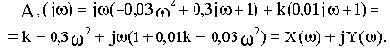
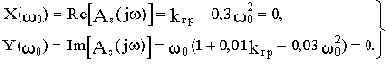
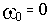 отбрасываем, т.к. для нахождения системы на границе устойчивости годограф Михайлова должен пройти через начало координат при
отбрасываем, т.к. для нахождения системы на границе устойчивости годограф Михайлова должен пройти через начало координат при 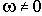 .
.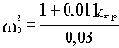
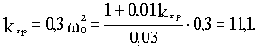
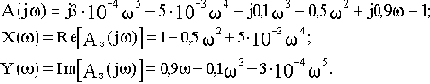
 от 0 до +
от 0 до +  , определим положительные корни уравнения X(
, определим положительные корни уравнения X( )=0:
)=0: 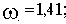
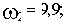 и неотрицательные корни уравнения Y(
и неотрицательные корни уравнения Y( )=0:
)=0: 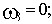
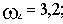
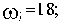
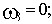 Y=0; X=1;
Y=0; X=1;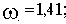 X=0; Y=0,9*1,41-0,1*1,413+0,0003*1,415=0,99;
X=0; Y=0,9*1,41-0,1*1,413+0,0003*1,415=0,99;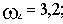 Y=0; X=1-0,5*3,22+0,005*3,24=3,6;
Y=0; X=1-0,5*3,22+0,005*3,24=3,6;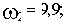 X=0; Y=0,9*9,9-0,1*9,93+0,0003*9,95=-59,59;
X=0; Y=0,9*9,9-0,1*9,93+0,0003*9,95=-59,59;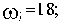 Y=0; X=1-0,5*182+0,005*184=364.
Y=0; X=1-0,5*182+0,005*184=364.
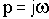 :
: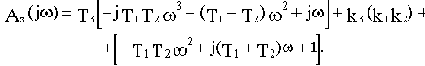

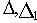 и
и 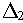 :
: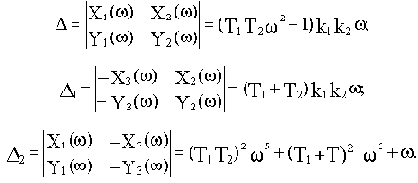
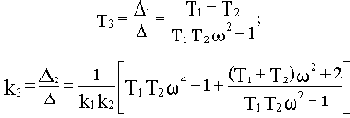
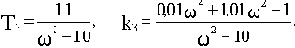

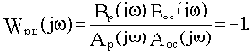
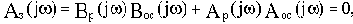
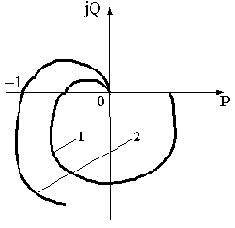
 .
.
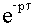 (при единичном коэффициенте передачи) включено последовательно с системой без запаздывания с передаточной функцией W0(p).
(при единичном коэффициенте передачи) включено последовательно с системой без запаздывания с передаточной функцией W0(p).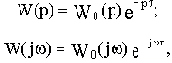
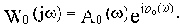
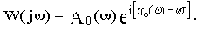
 САУ станет неустойчивой.
САУ станет неустойчивой. , что поясняется построением на рис.3.12.
, что поясняется построением на рис.3.12.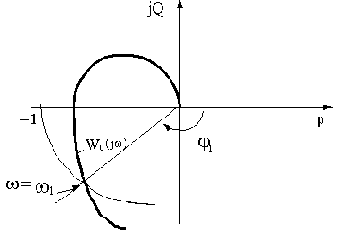
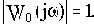 Частота, соответствующая этой точке -
Частота, соответствующая этой точке - 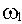 , а фаза -
, а фаза - 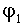 .
.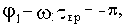
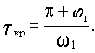
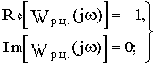 (3.8)
(3.8)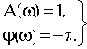 (3.9)
(3.9)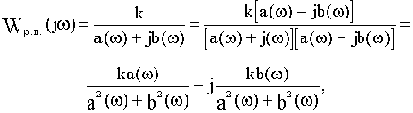
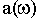 и
и 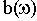 - соответственно действительная и мнимая части знаменателя
- соответственно действительная и мнимая части знаменателя 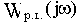 .
.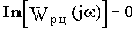 в том случае, если
в том случае, если 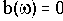 , значит
, значит
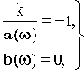 или
или 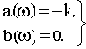 (3.10)
(3.10)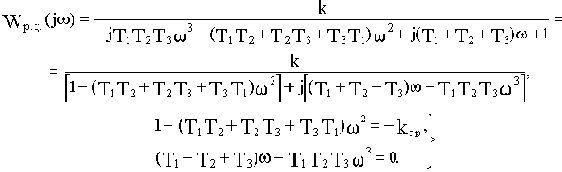
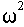 (корень
(корень  отбросим, т.к. по критерию Найквиста АФЧХ должна проходить через характерную точку при
отбросим, т.к. по критерию Найквиста АФЧХ должна проходить через характерную точку при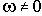 ) и подставим в первое уравнение:
) и подставим в первое уравнение:
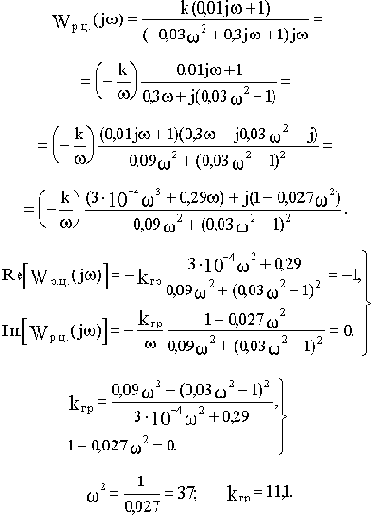
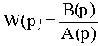 называют корни уравнения B(p)=0, т.е. такие значения р, при которых передаточная функция обращается в нуль, а полюсами - корни уравнения A(p)=0, т.е. такие значения р, при которых передаточная функция обращается в бесконечность.
называют корни уравнения B(p)=0, т.е. такие значения р, при которых передаточная функция обращается в нуль, а полюсами - корни уравнения A(p)=0, т.е. такие значения р, при которых передаточная функция обращается в бесконечность.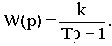
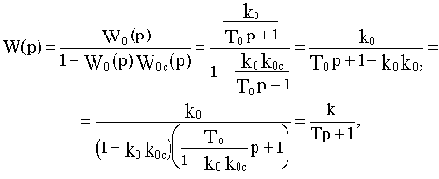
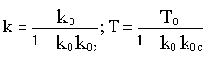
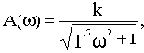
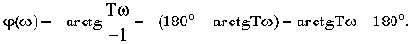
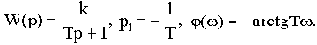
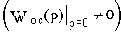 , гибкие - дифференцирующими
, гибкие - дифференцирующими 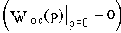 .
.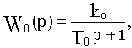

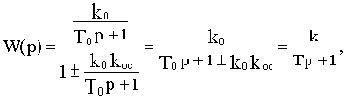

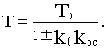

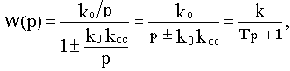
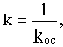
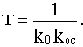
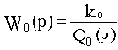 имеем:
имеем: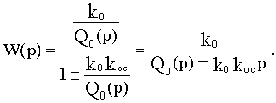

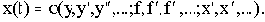
 . Процессы в УУ будут описываться двумя уравнениями:
. Процессы в УУ будут описываться двумя уравнениями: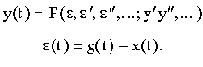
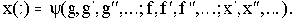
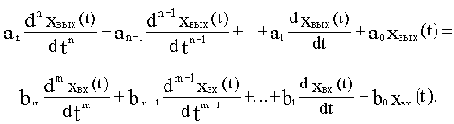
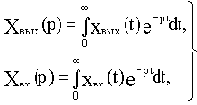 (2.2)
(2.2)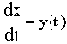 и согласно интегралу (2.2) найдем изображение:
и согласно интегралу (2.2) найдем изображение: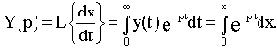
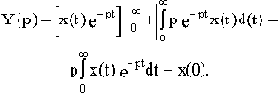
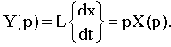
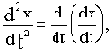 то
то 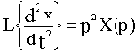 и т.д.
и т.д.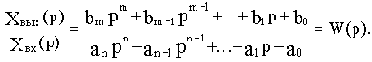 (2.4)
(2.4)

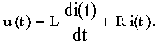
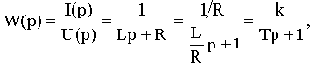

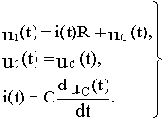
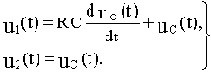
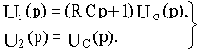
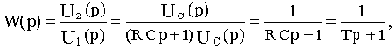

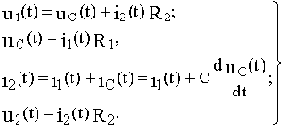
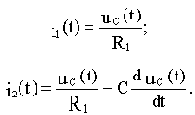
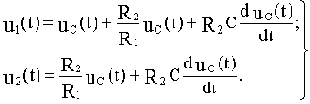
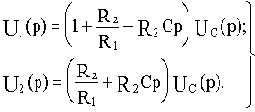
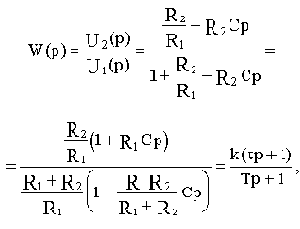
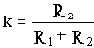 - коэффициент передачи,
- коэффициент передачи,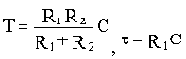 - постоянные времени.
- постоянные времени.
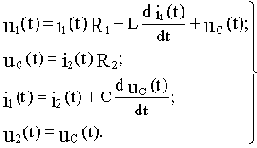
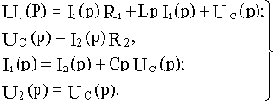
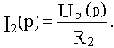
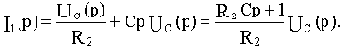
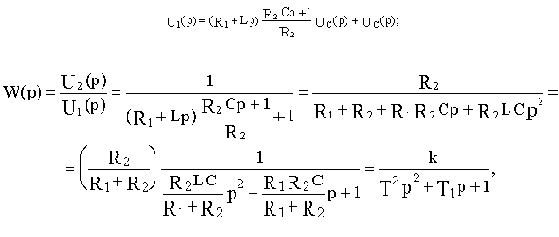
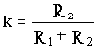 - коэффициент передачи,
- коэффициент передачи, - постоянные времени.
- постоянные времени.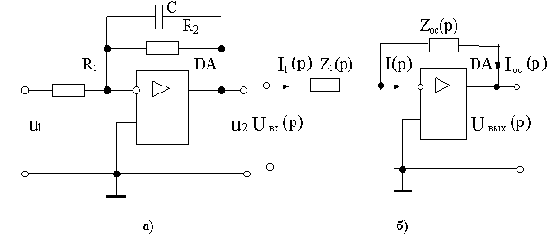
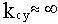 и
и 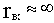 .
.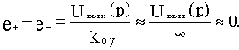
 и тогда
и тогда
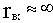 , можно считать
, можно считать 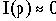 и, следовательно
и, следовательно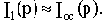
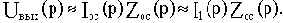
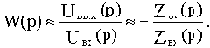 (2.5)
(2.5)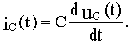
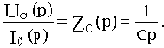
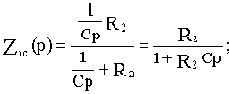 Z1(p)=R1;
Z1(p)=R1;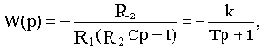

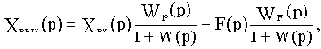
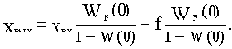
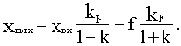 (4.1)
(4.1)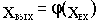 неоднозначна из-за наличия возмущения f. Статическая ошибка
неоднозначна из-за наличия возмущения f. Статическая ошибка 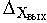 при неизменном задающем воздействии определяется выражением:
при неизменном задающем воздействии определяется выражением: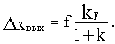
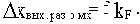

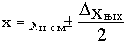 .
.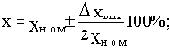 (4.2)
(4.2)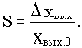
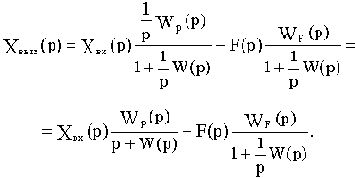
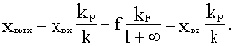
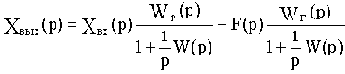
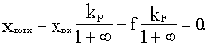
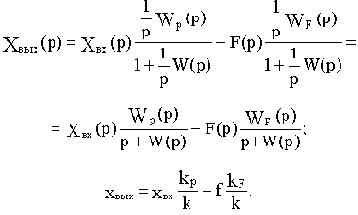
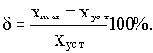

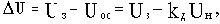 (в)
(в)
 (г)
(г)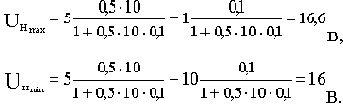
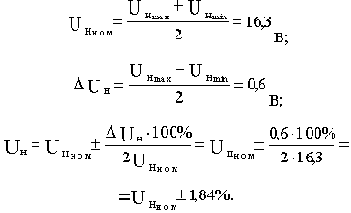
 1,84% от номинального значения.
1,84% от номинального значения.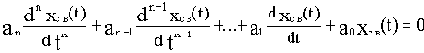

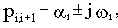
 может быть положительной или отрицательной величиной.
может быть положительной или отрицательной величиной.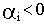 , эта составляющая будет затухать. Наоборот, при
, эта составляющая будет затухать. Наоборот, при 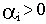 получатся расходящиеся колебания.
получатся расходящиеся колебания.
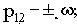
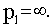
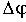 и запас устойчивости по амплитуде
и запас устойчивости по амплитуде 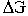 , которые показаны на рис.3.13.
, которые показаны на рис.3.13.
 , чтобы система оказалась на границе устойчивости.
, чтобы система оказалась на границе устойчивости.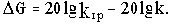 (3.11)
(3.11)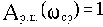 и затем найти
и затем найти 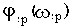 . Запас устойчивости по фазе будет равен
. Запас устойчивости по фазе будет равен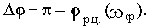 (3.12)
(3.12)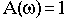 . Для нахождения этой точки графически следует из начала координат провести окружность радиусом R=1. Угол между этим лучем и отрицательной действительной полуосью и будет
. Для нахождения этой точки графически следует из начала координат провести окружность радиусом R=1. Угол между этим лучем и отрицательной действительной полуосью и будет 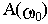 от границы устойчивости, т.е. от точки с координатами - 1, j0 (
от границы устойчивости, т.е. от точки с координатами - 1, j0 (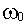 - это частота, при которой фаза составляет значение минус
- это частота, при которой фаза составляет значение минус 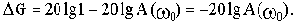

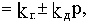
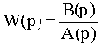
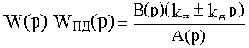
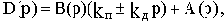
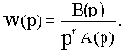


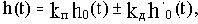
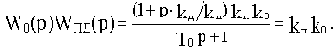

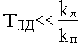



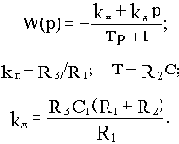
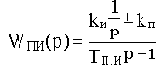
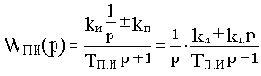

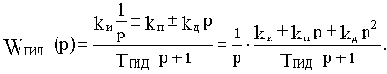

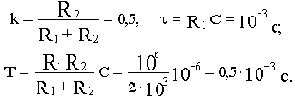
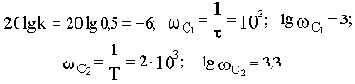


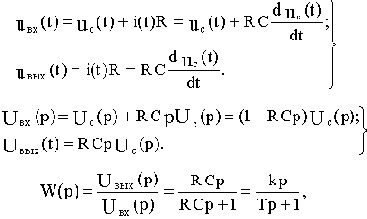
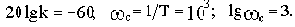
 и проводим через нее прямую с наклоном плюс 20 дБ/дек до сопрягающей частоты. После сопрягающей частоты наклон ЛАЧХ изменяется на минус 20дБ/дек, т.е. вторая асимптота идет горизонтально. Характеристика представлена на рис.2.22.
и проводим через нее прямую с наклоном плюс 20 дБ/дек до сопрягающей частоты. После сопрягающей частоты наклон ЛАЧХ изменяется на минус 20дБ/дек, т.е. вторая асимптота идет горизонтально. Характеристика представлена на рис.2.22.
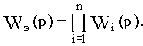
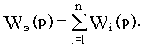

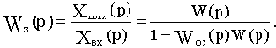



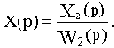
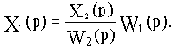
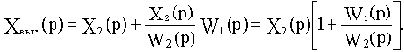
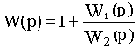 , как показано на рис. 2.10, б.
, как показано на рис. 2.10, б.
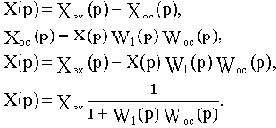
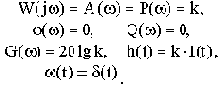
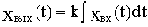 или
или 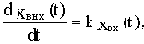
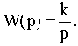
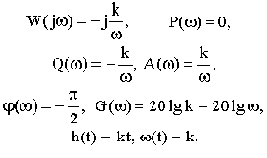
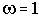 (при этом
(при этом 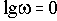 );
); 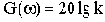 и провести прямую с наклоном минус 20 дБ/дек, так как с увеличением частоты на одну декаду ордината ЛАЧХ уменьшается на 20 дБ. (При каком-то значении
и провести прямую с наклоном минус 20 дБ/дек, так как с увеличением частоты на одну декаду ордината ЛАЧХ уменьшается на 20 дБ. (При каком-то значении 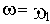 получаем
получаем 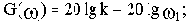 при увеличении частоты на одну декаду, т.е. при
при увеличении частоты на одну декаду, т.е. при 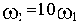 , соответственно
, соответственно 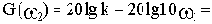
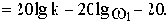 Разность этих ординат
Разность этих ординат 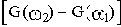 составляет минус 20 дБ).
составляет минус 20 дБ).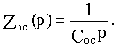


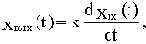 W(p)=kp.
W(p)=kp.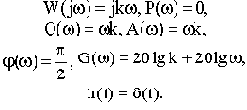

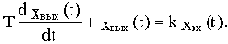
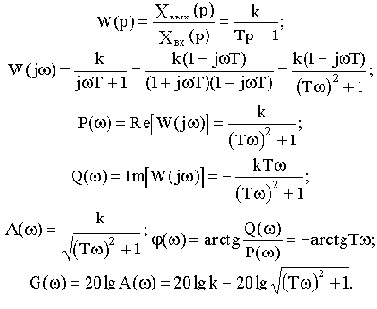
 и
и 
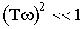 , то есть
, то есть  , следовательно
, следовательно 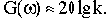
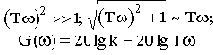
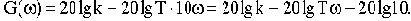
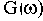 уменьшилась на 20lg10, т.е. на 20 дБ. Эта линия является асимптотой, к которой стремится ЛАЧХ при
уменьшилась на 20lg10, т.е. на 20 дБ. Эта линия является асимптотой, к которой стремится ЛАЧХ при 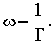 Поэтому эта частота называется сопрягающей частотой.
Поэтому эта частота называется сопрягающей частотой.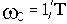 :
: дБ.
дБ. . При этом в точке
. При этом в точке 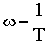 имеем
имеем 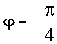 .
. в четвертом квадранте комплексной плоскости и центром в точке (
в четвертом квадранте комплексной плоскости и центром в точке (
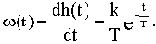

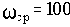 . Коэффициент передачи звена k=10. Требуется определить постоянную времени Т.
. Коэффициент передачи звена k=10. Требуется определить постоянную времени Т.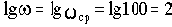 прямую с наклоном минус 20 дБ/дек до пересечения с горизонталью, проведенной на уровне
прямую с наклоном минус 20 дБ/дек до пересечения с горизонталью, проведенной на уровне 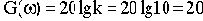 . Координата точки пересечения по оси частот даст логарифм сопрягающей частоты
. Координата точки пересечения по оси частот даст логарифм сопрягающей частоты 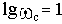 , отсюда
, отсюда 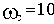 и
и 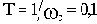 с.
с.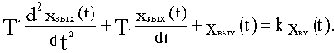
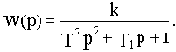

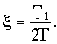
 . В зависимости от величины коэффициента демпфирования различают типы звеньев: колебательное (0<
. В зависимости от величины коэффициента демпфирования различают типы звеньев: колебательное (0< ).
).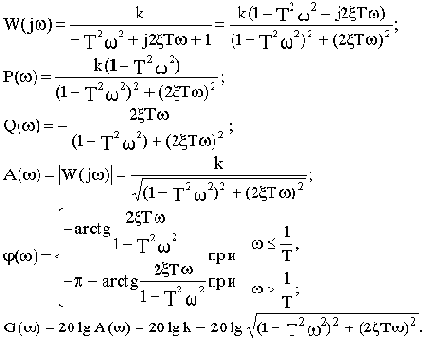
 <<1и в подкоренном выражении всеми членами. кроме 1, можно пренебречь. Тогда низкочастотная асимптота G(
<<1и в подкоренном выражении всеми членами. кроме 1, можно пренебречь. Тогда низкочастотная асимптота G(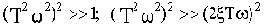 и в подкоренном выражении можно оставить лишь
и в подкоренном выражении можно оставить лишь  , пренебрегая остальными членами. Высокочастотная асимптота G(
, пренебрегая остальными членами. Высокочастотная асимптота G(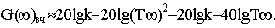
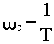 , как показано на рис.2.16.
, как показано на рис.2.16.
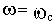 :
: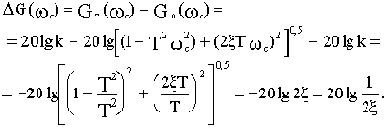
 точная ЛАЧХ идет ниже асимптотической при
точная ЛАЧХ идет ниже асимптотической при 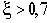 и выше - при
и выше - при 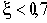 . При значениях
. При значениях  ошибка становится существенной (более трех децибел) и ее необходимо учитывать, используя приведенную выше формулу либо поправочные кривые из справочной литературы.
ошибка становится существенной (более трех децибел) и ее необходимо учитывать, используя приведенную выше формулу либо поправочные кривые из справочной литературы.
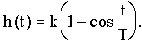
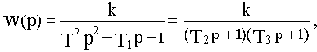
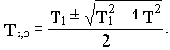
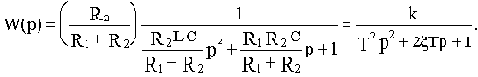
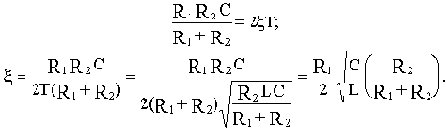
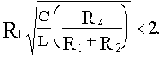
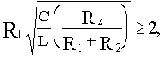
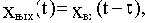
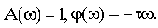
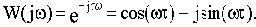


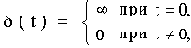

 в математике принято называть дельта-функцией.
в математике принято называть дельта-функцией. и называется импульсной переходной функцией или весовой функцией (функцией веса).
и называется импульсной переходной функцией или весовой функцией (функцией веса).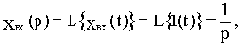
 (2.9)
(2.9)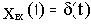 на выходе получаем импульсную переходную характеристику
на выходе получаем импульсную переходную характеристику  или в преобразованном по Лапласу виде:
или в преобразованном по Лапласу виде: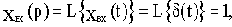
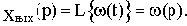
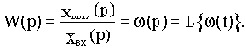 (2.10)
(2.10)

 Учет: Делопроизводство - Автоматизация - Софт
Учет: Делопроизводство - Автоматизация - Софт