Параллельное программирование

Нахождение последнего элемента списка

Одним из наиболее часто используемых способов организации информации в памяти ЭВМ является ее представление в виде списков, которые позволяют оперировать не с самими величинами, а с их адресами, что облегчает программирование, экономит память и сокращает затраты на пересылку информации. С помощью списков удобно отображать данные самой разнообразной структуры: множества, деревья, графы, строки и т.д.
Основными операциями над списками являются: получение доступа к произвольному элементу списка; включение нового элемента в заданное место списка и исключение его оттуда; сортировка элементов списка; поиск элемента с заданными свойствами и другие. Простота их реализации является одним из наиболее привлекательных свойств списковой организации данных. Однако традиционное представление списков на основе ссылок предполагает последовательную обработку их элементов. Все известные алгоритмы, реализующие операции над списками, являются последовательными и ориентированы на однопроцессорные ЭВМ фон-неймановской архитектуры.
Эффективная реализация операций над списками для параллельных вычислительных систем представляет непростую (а для некоторых архитектур — например, векторно-конвейерной — и неразрешимую) задачу. Особый интерес представляла бы разработка таких алгоритмов для ВС с большим числом процессорных элементов.
Под списком L будем понимать совокупность объектов вида In =(V, C), где V — ссылка на данные, C — ссылка на некоторый (следующий) элемент этого же списка. Последний элемент списка имеет своим значением nil, т.е. пустую ссылку.
Пусть элементы каждой двойки (V, C) расположены в памяти так, что их адреса определяются сложением фиксированного смещения с некоторым базовым адресом. Тогда совокупность всех двоек можно рассматривать как массив R — образ списка, в котором места расположения каждого элемента могут быть рассчитаны.
Интуиция подсказывает, что параллельная обработка списка невозможна, поскольку в общем случае необходимо вычислить адреса k предыдущих элементов списка, прежде чем станет доступен (k+1)-й элемент.
Однако, она становится возможной, если использовать образ списка.

Модифицируем представление каждого элемента массива R, введя дополнительное поле D, в которое заносится ссылка на соответствующее поле того элемента списка, ссылка на который содержится в поле C. Строить образ списка целесообразно одновременно с формированием и изменением самого списка. Таким образом, элемент образа списка превращается в тройку (F, C, D). На рис. 1.1

структура элемента образа списка представлена в графической форме.


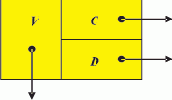
Рис. 1.1.  Элемент образа списка

На рис. 1.2,а изображен список, соответствующий записи L = (A B E F G H Г) (для простоты считаем, что он не содержит подсписков).


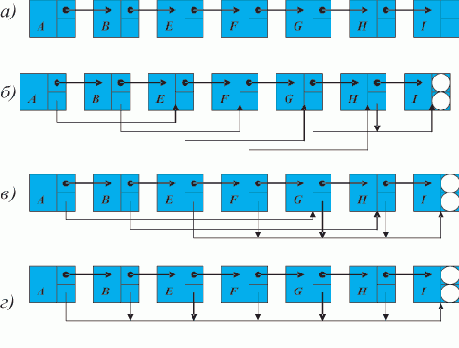
Рис. 1.2.  Пошаговое нахождение последнего элемента списка (последовательное расположение элементов в памяти)

Пусть над всеми его элементами последовательно, начиная с головы, производится следующее действие: поле D текущего элемента принимает значение того поля D, на которое указывает содержащаяся в нем ссылка (если в поле D содержится ссылка на пустой элемент, то его значение не изменяется). В результате список L примет вид, показанный на рис. 1.2,б. Вид списка L после второго прохода показан на рис. 1.2,в. И, наконец, после третьего прохода поле D головы списка будет содержать ссылку на последний элемент списка L, на чем выполнение алгоритма заканчивается (рис. 1.2,г).

Предположим теперь ситуацию, когда элементы списка расположены в памяти в произвольном порядке, например, так, как показано на рис. 1.3,а.


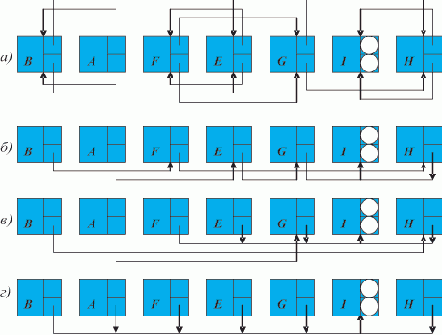
Рис. 1.3.  Пошаговое нахождение последнего элемента списка (произвольное расположение элементов в памяти)

Важно, что преобразования не изменяют структуру списка, поскольку действия производятся над "избыточной" информацией; при этом на правильность выполнения алгоритма не влияет порядок расположения элементов в памяти.

Заметим теперь, что все операции над образом списка R, производимые во время одного прохода, могут быть выполнены параллельно и независимо друг от друга, то есть, при наличии достаточного вычислительного ресурса, за один временной шаг.


Таким образом, мы получаем доступ к последнему элементу списка за log2N шагов. Аналогичные алгоритмы, также использующие информационную избыточность, могут быть построены и для других операций над списками.

Реализация операций над списками для локально-асинхронной ВС, каковой является ВС SPMD-архитектуры, допускает использование принципа монопрограммирования, т.е. составления единственной программы, запускаемой на всех процессорах одновременно. Здесь мы приведем монопрограмму нахождения последнего элемента списка и проследим процесс ее выполнения. Она выбрана потому, что нахождение последнего элемента является частью многих операций над списками. Например, для объединения списков L1 и L2 достаточно найти последний элемент списка L1 и заменить в его поле C пустую ссылку ссылкой на первый элемент списка L2.

Как говорилось выше, для организации параллельной обработки целесообразно использовать образ R списка — массив информации об элементах списка, содержащий сведения о его структуре и преемственности элементов. Отметим, что упорядоченность элементов массива R в памяти в общем случае может не совпадать с логической упорядоченностью элементов списка, задаваемой ссылками. Это позволяет достаточно просто интерпретировать выполнение операций над списками. Например, при добавлении новых элементов в список L нет необходимости вставлять новый элемент массива R в какую-либо конкретную позицию - можно просто добавить его в конец массива. Аналогично, при исключении элемента из L вместо уплотнения массива R на освободившееся место можно записать его последний элемент.

Обработку списка, таким образом, мы сводим к обработке массива, представляющего его образ. Этот массив, в свою очередь, может описываться дескриптором.

Дескриптор DR массива R={V,C,D}1^N в полной комплектации, как рассматривалось ранее, состоит из восьми элементов: DR={DRO , ..., DR7}. Дескрипторный элемент DRO содержит адрес a0 первого элемента массива, DR1 — шаг h = 3 переадресации, DR2 — количество N элементов массива, в DR3 находится адрес последнего элемента массива.


Элемент DR4 служит для переадресации при последовательном обращении к данному массиву. В нем хранится адрес aQ+jh для выработки элемента массива при j-м (j = 0,1 , ..., n-1) обращении к массиву. При каждом обращении к массиву по некоторым командам этот адрес увеличивается на шаг h (т.е. выполняется операция j := h+!). Остальные дескрипторы предназначены для организации распределения элементов массива между процессорами. DR5

содержит значение адреса aQ+ih, i = 0,1 , ..., n-1, т.е. каждый процессор Пi формирует и использует свое значение (DR5), располагая адресом регистра, содержащего значение номера i процессора, для начального обращения к "своему" элементу массива. DR6 содержит значение nh, используемое для переадресации к следующему "своему" элементу массива с учетом числа процессоров в ВС. В DR7 содержится значение адреса aQ+ih+jnh=(DR5)+j(DR6), используемое для возможности переадресации при последовательном (j = 0,1,...) обращении к массиву. Если нет необходимости, могут формироваться не все дескрипторные элементы.

Предположим, как и ранее, что в ВС реализована трехадресная система команд вида: ? I1 A1 12 A2 I3 A3, где ? — код операции, I1, I2, I3 — адреса модификаторов, дескрипторных элементов или дескрипторов, A1, A2, A3 — смещения. При выполнении команд формируются исполнительные адреса: A'r =(Ir)+ Ar, r = 1,2,3.

Для упрощения операций над дескрипторами в систему команд введены специальные команды, обеспечивающие переадресацию для различных дисциплин выбора "своих" элементов обрабатывающим процессором, анализ выхода за пределы массива, инвариантность программы относительно размера массива.

Монопрограмма нахождения последнего элемента списка представлена в табл. 1.2.

Таблица 1.2. №kКОПI1A1I2A2I3A30123456789101112

СИНХ
ЗАГ	K
ПРАД	DR7					012
УП0	K					012
ЗАПК	DR7	0003				M
УП=0		M				011
ЗАПК		M			DR7	0003
ИЗМАД	DR7					009
БП		003
ЗАГ	DR7	DR5
БП		0003
ЗАП	DR7	0003				K
В

Команда O (СИНХ) синхронизирует процессоры для одновременного начала выполнения программы (это не влияет на правильность работы ВС, а лишь упрощает контроль выполнения).


Каждый процессор посылает сигнал на устройство СИНХ; после поступления сигналов от всех процессоров выдается обратный сигнал, по которому процессоры приступают к выполнению следующей команды.

Команда 1 (ЗАГрузка модификатора) обнуляет модификатор K, в который впоследствии одним из процессоров будет записан адрес последнего элемента списка.

Команда 2 (ПРоверка АДреса) сравнивает значение дескрипторного элемента DR1, первоначально равное a0+3i, с адресом последнего элемента массива, записанным в дескрипторном элементе DR3. Этим устанавливается возможность загрузки i-го процессора (возможен случай i>N). Если процессор не будет занят обработкой списка, то управление передается команде 12 на Выход из процедуры. В противном случае с команды 3 начинается цикл обработки элементов списка, а точнее — его последовательности ссылок. Команда 3 осуществляет Условный Переход на выход из процедуры по отличному от нуля значению K.

Команда 4 выполняется при нулевом значении K, она осуществляет ЗАПись по Косвенному адресу. При этом производится косвенное считывание по первому адресу (DR7) + 0003, т.е. по адресу ((DR7)+0003), и запись по адресу модификатора M.

Команда 5 проверяет, пуста ли выбранная ссылка. Если пуста, то анализируемый элемент списка - последний; управление передается команде 11, записывающей адрес этой ссылки в K. Если не пуста, т.е. (M)\neq 0, то выполняется команда 6 и ее значение записывается вместо значения текущей ссылки.

Команда 7 ИЗМенение АДреса задает операцию (DR7):=(DR7)+(DR6) и если полученное значение превышает (DR3), передает управление команде 9. Таким образом, каждый процессор осуществляет переадресацию для последующей выборки "своего" адреса ссылки из массива таких адресов. Если при этом массив не исчерпан, то команда 8 (Быстрый Переход) передает управление на команду 3 — продолжение цикла подстановки ссылок. Если переадресация выводит из массива, то команда 9 восстанавливает дескрипторный элемент DR7 , т.е. выполняется операция (DR7):= (DR5) = a0+3i.


По команде 10 управление передается на следующий цикл подстановки ссылок.

Команда 11 выполняется, если при выполнении команды 5 обнаружилось, что найдена пустая ссылка, адрес которой записывается в K. После выполнения в последующем команды 3 всеми процессорами закончится и выполнение программы.

Рассмотрим процесс счета программы нахождения последнего элемента списка L, содержащего семь элементов, на ВС, имеющей в составе три процессора — П0, П1 и П2.

Каждый процессор выполняет свою копию программы, обладая при этом собственным набором дескрипторов, отличающихся друг от друга только значениями дескрипторных элементов DR5 и DR7. Согласно принятому нами представлению образа списка и порядку его обработки, процессор П0 будет обрабатывать элементы списка A, F и I, процессор П1 — B и G, и процессор П2 — элементы E и H. Пусть каждая команда программы выполняется за одинаковое время — условный такт, и при обращении к памяти не возникает конфликтов (все элементы образа списка расположены в разных блоках памяти).

На рис. 1.4 показана диаграмма потактового выполнения программы на каждом из процессоров, полученная при справедливости этих предположений. Некоторое время все процессоры работают синхронно: такты 1—3 — начальные действия; такты 4—9 — первый цикл подстановки ссылок, во время которого изменяются поля D элементов A, B и E; такты 10—12 — начало второго цикла подстановки ссылок.


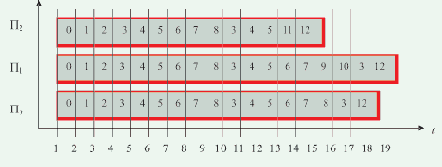
Рис. 1.4.  Временная диаграмма выполнения программы нахождения последнего элемента списка

Во время второго цикла подстановки ссылок процессор П2 обнаруживает пустую ссылку (т.е. последний элемент списка) в такте 12 и, записав его адрес в модификатор K (такт 13), заканчивает свою работу в следующем такте командой Возврат.

Процессор П0 заканчивает второй цикл подстановки ссылок (такты 13—15), не обнаружив пустой ссылки, но завершает свою работу в тактах 16 и 17, поскольку модификатор K получил уже к этому времени ненулевое значение.

Процессор П1 в такте 14 изменяет значение дескрипторного элемента DR7 и, так как оно выводит за границы обрабатываемого массива, в такте 15 восстанавливает его исходное значение.


Далее следует переход на начало третьего цикла обработки ссылок (такт 16), но, обнаружив ненулевое значение модификатора K (такт 17), в следующем такте процессор П1 также завершает свою работу. Результатом совместной работы трех процессоров является адрес ссылки на последний элемент списка, записанный в модификаторе K.

Заметим, что детерминированный — при синхронной работе процессорных элементов — процесс выполнения алгоритма при реализации на локально-асинхронной ВС приобретает некоторую неопределенность. Дело в том, что мы не можем быть уверены в порядке выполнения процессорами операций замены значений ссылок (команда 6), поскольку в принципе не исключены обращения к одним и тем же модулям общей памяти. В результате какой-либо процессор может "подхватить" уже обновленную ссылку. Однако очевидно, что это только приблизит окончание работы алгоритма, который в таком случае как бы "перескакивает" через некоторые шаги. Например, элемент A, обрабатываемый процессором П0, после первого выполнения процессором команды 6 должен содержать ссылку на элемент E. Но если процессор П1 успел по какой-либо причине выполнить свою аналогичную операцию раньше, элемент A будет содержать ссылку на более "удаленный" от него элемент F. Поэтому появляется возможность более раннего достижения условия окончания работы программы.

Здесь иллюстрируется не всегда ясно сознаваемый факт, что принципы параллельной обработки информации могут быть использованы для нахождения самого общего решения задач, по своей природе, казалось бы, не распараллеливаемых. Эффективность параллельной обработки списков в данном случае достигается двумя встречными путями: дополнением традиционного подхода концепцией обработки массивов и использованием архитектурных особенностей ВС, реализующей SPMD-технологию.

Поиск и исключение элемента списка

Пусть задано имя S некоторого элемента списка, являющееся первым словом в массиве его данных, на которое указывает одна из ссылок C в массиве R троек (V, C, D). Необходимо по заданному S найти соответствующий ему элемент списка, т.е. такой, данные которого начинаются с S, и исключить его из списка. Для этого достаточно заменить значение ссылки C в одной из троек в массиве R, указывающей на исключаемый элемент, на значение ссылки, указанное в тройке, которая соответствует исключаемому элементу. При этом тройка, соответствующая исключаемому элементу, в свою очередь должна быть исключена из массива R.
Совместные действия процессоров можно организовать следующим образом.
Пусть все процессоры "смотрят" на соответствующие им по номеру (а затем — кратные им по номеру) элементы массива R. Какой-то из них найдет элемент, ссылка в котором указывает на элемент списка, где первое слово совпадает с S. Эта ссылка заменяется тем же процессором на ссылку, указанную в исключаемом элементе, а сам элемент массива R, соответствующий исключенному элементу, исключается из R. После этого корректируется дескриптор, соответствующий массиву R.
Проанализируем работу программы, представленной в табл. 1.3.

Таблица 1.3. №kКОПI1A1I2A2I3A3012345678910111213

СИНХ
						003
ЗАГ	K
ПРАД	DR7					010
ЗАП	DR7	0002				M1
ЗАПК	M1	0001				M2
		M2		S		011
ЗАГ	K	0001
ЗАП	M1	0002			DR7	0002
ИСКЛ	DR		M1
В
	K					010
ИЗМАД	DR7					010
БП		004

По команде 0 производится синхронизация процессоров ВС.
По командам 1 и 2 модификатору K присваивается нулевое значение. Эту операцию выполняет процессор 0. Другие процессоры по команде 1, в которой номер i процессора сравнивается с нулем и выполняется условный переход по неравенству, перейдут к выполнению команды 3. (Иллюстрируется возможность параллельной работы процессоров по разным ветвям монопрограммы.)
По команде 3 осуществляется выход из программы, если значение текущего адреса в дескрипторном элементе DR7 превосходит значение текущего адреса последнего элемента массива R, записанное в DR3. Если DR7 DR3, по команде 4 в регистр M заносится ссылка анализируемого элемента списка, записанная по адресу (DR7) + 2, т.е. в поле C.
Пусть ссылка, записанная в поле C, указывает на первый адрес в тройке, составляющей некоторый элемент R. Тогда по адресу (M1) + 1 находится адрес начала "тела" соответствующего элемента списка. Команда 5 выполняет запись по косвенному адресу этого начала в регистр M2.
По команде 6 начало тела анализируемого элемента списка сравнивается с исключаемым элементом, указанным в S.
При положительном результате сравнения по команде 7 модификатору K присваивается отличное от нуля значение, служащее индикатором того, что исключаемый элемент списка некоторым процессором найден. Если (M2) S, управление передается команде 11.
По команде 8 ссылка, записанная в элементе массива R и соответствующая исключаемому из списка элементу, присваивается тому элементу, который ранее указывал на исключаемый, т.е. значение ((M1) + 2) присваивается элементу (DR7) + 2.
Команда 9 — ИСКЛючение из массива, описываемого дескриптором DR, элемента, расположенного по адресу (M1). В результате выполнения команды 4 по данному адресу находится элемент массива R, соответствующий исключаемому из списка элементу.
По команде 10 производится выход из подпрограммы.
Команда 11 получает управление в случае, если ссылка в анализируемом элементе массива R не указывает на исключаемый из списка элемент. В этом случае проверяется наличие признака того, что некоторый процессор обнаружил искомый элемент и готов исключить его из списка, т.е. если (K) 0, осуществляется выход из подпрограммы по команде 10. Если (K) = 0, необходимо перейти к анализу следующего элемента массива R, предопределенного i-му процессору.
По команде 12 выполняется переадресация (DR7) := (DR7) + (DR6), где (DR6) = Nh. Если такая переадресация приводит к выходу за пределы массива, т.е. новое значение DR7 превышает значение последнего адреса массива R, указанное в DR3, производится выход из подпрограммы по команде 10.
В противном случае по команде 13 процессор приступает к анализу очередного элемента R.
В данном случае нам не пришлось в полной мере использовать существующие в системе средства синхронизации. Легко усложнить пример, рассмотрев случай, когда одновременно заданы несколько исключаемых элементов. Их исключение должно производиться последовательно, т.к. процессор, обнаруживший исключаемый элемент, должен располагать вполне определенной информацией о текущем состоянии списка, изменяемом в процессе исключения из него элементов. Ведь после каждого исключения может измениться и порядок последующего назначения элементов массива R на обработку процессорами.
Это приводит к необходимости выделения одной или группы команд исключения из списка (см. команду 9 данной монопрограммы) в критический блок, не допускающий одновременного обращения к нему более одного процессора. Формирование критического блока достигается выполнением в его начале команды ЗАКРыть Семафор с указанием адреса некоторого семафора C. Если при выполнении этой команды данный семафор уже закрыт другим процессором при выполнении этого же фрагмента программы, то процессор переходит в режим ожидания, "жужжания", т.е. повторного выполнения этой команды до открытия семафора.
Критический блок заканчивается командой ОТКРыть Семафор с указанием адреса того же семафора.

Реализация языка логического программирования ПРОЛОГ на ВС SPMD-архитектуры

Рассмотрим упрощенную задачу в виде ПРОЛОГ-программы, содержащую все характерные элементы решения задачи удовлетворения (сложной) цели на основе базы знаний.
Задан фрагмент БЗ, содержащий факты и правила.
(Факты-клозы (отдельные предикаты-высказывания принято называть клозами), которые не содержат правых частей, правила-клозы, которые содержат правые части; одноименные факты и правила объединяются в процедуры.) Для единообразия и в соответствии с исключением факта из цели при связывании переменных обозначим факты так же, как и правила, но с "пустыми" правыми частями.
База знаний
Процедура "мужчина": мужчина (иван):- мужчина (василий):- мужчина (петр):- мужчина (федор):- мужчина (юрий):-
Процедура "женщина": женщина (марья):- женщина (ирина):- женщина (ольга):- женщина (елена):-
Процедура "родитель": родитель (марья, иван):- (Читать: "Марья — родитель Ивана") родитель (иван, елена):- родитель (марья, василий):- родитель (федор, марья):- родитель (петр, ирина):- родитель (петр, иван):- родитель (федор, юрий):-
Процедура "мать": мать (X, Y):-женщина (X), родитель (Y)
Процедура "отец": отец (X, Y):-мужчина (X), родитель (Y)
Процедура "брат": брат (X, Y):-мужчина (X), родитель (P,X), родитель(P,Y), X <> Y
Процедура "сестра": сестра (X, Y):-женщина (X), родитель (P,X), родитель(P,Y), X <> Y
Процедура "дядя": дядя(X,Y):-брат(X,P), родитель(P,Y)
Пусть задана некоторая сложная (т.е. опирающаяся не на факт, а требующая вывода) цель, с которой мы обратились в эту БЗ, например
дядя (X, Y) (запись цели образует фрейм
решение которой (вывод) заключается в нахождении всех пар переменных (имен объектов) X и Y, для которых справедливо утверждение
"X является дядей Y".
Для решения такой задачи используется прием трансформации цели, который заключается в рекурсивном переборе различных вариантов подстановки вместо предикатов, составляющих сложную цель, правых частей клозов соответствующей процедуры.
Производится фиксация варианта связывания переменных и унификация, при которой отбрасываются несовместимые варианты связывания, т.е. противоречащие фактам и правилам. Варианты связывания всех переменных, прошедшие все этапы унификации, являются решением.

Т.е. для решения данной задачи необходимо действовать следующим образом.

Находим первый (и единственный) предикат цели дядя (X, Y). Находим в БЗ процедуру с этим именем и заменяем найденный предикат правой частью этой процедуры. Получим трансформируемую цель — фрейм

брат (X, P), родитель (P, Y).

К первому предикату этого фрейма применяем аналогичные действия, получаем фрейм

мужчина (X), родитель (Q, X), родитель (Q, P), X <> P, родитель (P,Y)

(Во избежание коллизии, развивая фрейм цели, вводим новые переменные, отличные от тех, которые до этого уже были использованы.)

Вновь входим в процедуру с именем первого предиката цели. Начинаем первый уровень ветвления. А именно, первый клоз там — факт мужчина (иван). С его помощью производим первое связывание переменных, т.е. подстановку конкретного значения. Предикат цели, породивший факт, т.е. это связывание, может быть из трансформируемой цели исключен, т.е. заменен своей "пустой" правой частью:

родитель (Q, иван), родитель (Q, P), иван <> P, родитель(P,Y)

Обращаемся к процедуре "родитель", начиная второй уровень ветвления. Первый клоз этой процедуры родитель (марья, иван) определяет дальнейшее связывание переменных:

родитель (марья, Р), иван <> P, родитель (P, Y).

Вновь входим в процедуру "родитель"(третий уровень ветвления), находим клоз shape родитель (марья, иван). Трансформируем цель — получаем новый фрейм:

иван <> иван, родитель (иван, Y).

Имеем противоречие, т.е. не проходит унификация.

Ищем на данном шаге ветвления другой вариант связывания, находим следующий клоз

родитель (марья, василий)

Трансформируем цель:

иван <> василий, родитель (василий, Y) родитель (василий, Y).

Вновь входим в процедуру "родитель", но не находим там клоза, в котором василий указан как чей-либо родитель.


Т.е. вновь не проходит унификация — установление совместимости варианта связывания переменных.

Возвращаемся на шаг ветвления назад. (Реализуем стратегию поиска с ветвлением и возвращением назад — backtraking) На втором уровне ветвления пробуем клоз, в котором иван указан как сын: родитель (петр, иван). Цель трансформируется в следующий фрейм

родитель (петр, Р), иван <> P, родитель (P, Y).

Вновь (на третьем уровне ветвления) обращаемся к процедуре "родитель" и выбираем первый клоз, в котором петр указан как отец — родитель (петр, ирина). Цель трансформируется:

иван <> ирина, родитель (ирина, Y) родитель (ирина, Y)

Входим в процедуру "родитель", но не находим там клоза, в котором ирина указана как родитель. (Не проходит унификация.)

Возвращаемся на второй уровень ветвления и не находим там больше клозов, где иван указан как сын. Возвращаемся на первый уровень ветвления и в процедуре "мужчина" выбираем для последующего испытания следующий клоз мужчина (василий). Цель принимает вид (фрейм)

родитель (Q, василий), родитель (Q, P), василий <> Р, родитель (P, Y).

Теперь на втором уровне ветвления находим первый (и единственный) клоз, в котором василий указан как сын. Цель трансформируется в соответствии с новым связыванием переменных, обусловленным найденным клозом родитель (марья, василий):

родитель (марья, Р), василий <> P, родитель (P, Y).

На третьем уровне ветвления находим первый клоз, где марья — родитель: родитель (марья, иван). Связываем тем самым переменные, цель трансформируется

василий иван, родитель (иван, Y) родитель (иван, Y).

Находим в процедуре "родитель" первый клоз, в котором иван указан как родитель - родитель (иван, елена). Цель выродилась, значит

дядя (X, Y) = дядя (василий, елена) — одно из решений задачи.

Продолжив перебор так, словно на данном шаге унификация не прошла, можно найти остальные решения : дядя (юрий, иван), дядя (юрий, василий).

В основе распараллеливания решения этой задачи лежит способ размножения вариантов на основе трансформации цели.


Способ обеспечивает: отсутствие "backtracing'а" (ветвление есть, а возврата назад нет); простоту самой процедуры вывода; возможность неограниченного использования ИЛИ-параллелизма (одновременной независимой обработки многих вариантов связывания переменных); конвейерную реализацию И-параллелизма (распараллеливания обработки одного варианта связывания переменных на конвейере, т.к. каждый раз обрабатывается лишь первый предикат каждого фрейма). Поясним это подробнее.

Пусть в общей памяти ВС размещен пул фреймов - промежуточных результатов трансформации цели, т.е. варианты связывания переменных. Отсюда уже видно, что в системе формируется не один очередной, а сразу несколько вариантов преобразования цели, а затем — и преобразования образующихся фреймов.

Первоначально этот пул образует единственный фрейм — цель. Все процессоры "смотрят" на пул фреймов, и каждый процессор выбирает для обработки тот из них, первый предикат в котором допускает замену его правой частью в процедуре с именем этого предиката.

Произведя преобразование этого предиката, процессор производит унификацию (т.е. анализ на непротиворечивость варианта связывания переменных) и при ее успешном выполнении дополняет сформированным фреймом пул фреймов, отдельно размещая соответствующий этому фрейму вариант связывания переменных.

Допустимо согласование работы процессоров, такое, при котором два процессора, выбрав один и тот же фрейм, произведут разную замену исходя из количества клозов в соответствующей процедуре. Для этого при каждом фрейме указывается информация о количестве процессоров (формируется счетчик), которые могут одновременно (условно, т.к. с участием этого счетчика начала обращений процессоров к одной процедуре образуют последовательность) приступить к обработке этого фрейма.

Ясно, что таким образом легко и естественно реализуется так называемый ИЛИ-параллелизм на основе размножения и одновременной обработки вариантов трансформации цели. При этом явная реализация "backtraking'а" не нужна: она сдерживала бы возможности распараллеливания.


В то же время обработка каждого фрейма одним процессором заключается в преобразовании единственного — первого предиката. Таким образом, в целом каждый фрейм подвергается конвейерной обработке — реализуется конвейерный способ И-параллелизма.

Процесс размножения вариантов не может привести к беспредельной загрузке памяти, т.к., во-первых, многие варианты отсекаются процедурой унификации; во-вторых, фреймы, в которых первые предикаты обработаны, могут быть исключены из пула: они породили все возможные новые фреймы; в-третьих, на основе некоторых фреймов, в частности, при их вырождении, выдается заключение о решении.

Таким образом, возможен динамический возврат памяти в систему.

Пусть ВС содержит 8 процессоров (0—7). Тогда процесс параллельной обработки цели в нашем примере можно представить табл. 1.1.

Таблица 1.1. № полученного фрейма№ обработанного фреймаОбрабатывающие процессыПул фреймовСчетчикСвязывание переменных

0			дядя(X,Y) (ЦЕЛЬ)	1	X=?, Y=?
1	0	0	брат(X,P), родитель(P,Y)	1
2	1	1	мужчина(X), родитель(Q,X), родитель(Q,P), X <> P,родитель(P,Y)	5
3	2	0	родитель(Q,иван), родитель(Q,P), иван <> P, родитель(P,Y)	7	X=иван, Y=?
4	2	2	родитель(Q,василий), родитель(Q,P), василий <> P, родитель(P,Y)	7	X=василий, Y=?
5	2	3	родитель(Q,петр), родитель(Q,P), петр <> P, родитель(P,Y)	7	X=петр, Y=?
6	2	4	родитель(Q,федор), родитель(Q,P), федор <> P, родитель(P,Y)	7	X=федор, Y=?
7	2	5	родитель(Q,юрий), родитель(Q,P), юрий <> P, родитель(P,Y)		X=юрий, Y=?
8	3	6	родитель(марья,P), иван <> P, родитель(P,Y)	7	X=иван, Q=марья, Y=?
	3	7,0,1,2	не проходит унификация
9	3	3	родитель(петр,P), иван <> P, родитель(P,Y)	7	X=иван, Q=петр, Y=?
	3	4	не проходит унификация
	4	5,7	не проходит унификация
10	4	0	родитель(марья,P), василий <> P, родитель(P,Y)	7	X=василий, Q=марья, Y=?
	4	1,2,4,6	не проходит унификация
	5	3,5,7,1,2,4,6	не проходит унификация (у петра нет родителей)
	6	0,1,2,3,4,5,6	не проходит унификация
	7	7,0,1,2,3,4	не проходит унификация
11	7	5	родитель(федор,P), юрий <> P, родитель(P,Y)	7	X=юрий, Q=федор, Y=?
	8	6	не проходит унификация
	8	7	не проходит унификация
12	8	0	родитель(василий,Y)	7	X=иван, Q=марья, P=василий
	8	1,2,3,4	не проходит унификация
	9	5,7,1,2	не проходит унификация
13	9	3	родитель(ирина,Y)	7	X=иван, Q=петр, P=ирина
	9	4,6	не проходит унификация
14	10	0	родитель(иван,Y)	7	X=василий, Q=марья, P=иван
	10	1,2,5,6,7,3	не проходит унификация
	11	4,1,3	не проходит унификация
15	11	5	родитель(марья,Y)	7	X=юрий, Q=федор, P=марья
	11	6,7,0	не проходит унификация
	12	2,5,6,7,3,1,4	не проходит унификация
	13	0,1,2,3,4,5,6	не проходит унификация
	14	0	не проходит унификация
	14	1	цель исчерпана, решение:		X=василий,Y=елена
	14	2,3,4,5,6	не проходит унификация
	15	0	цель исчерпана, решение:		X=юрий,Y=иван
	15	1	не проходит унификация
	15	2	цель исчерпана, решение:		X=юрий,Y=василий
	15	3,4,5,6	не проходит унификация

Здесь порядок загрузки процессоров обусловлен немедленной выборкой фрейма, как только он получен. Выбрать другой процессор может раньше, чем тот процессор, который его получил, т.к. ему еще надо закончить программный цикл после записи в БЗ.

Параллельное программирование

Архитектуры ротационных БД

Сервер отсутствует. На рис. 2.1 представлена временная диаграмма работы (в начальный момент) ротационной базы данных в ЛВС, в составе которой отсутствует сервер. Сеть содержит n рабочих станций, по числу которых БД разбита на n сегментов.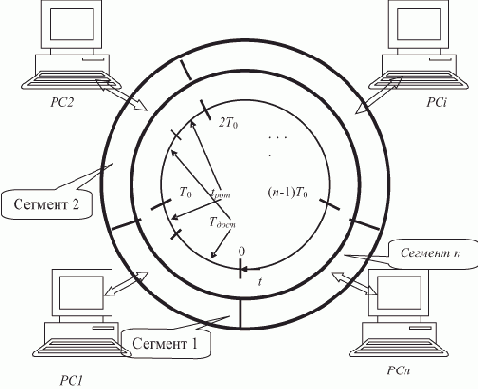

Рис. 2.1.  Ротация сегментов БД
Круговая шкала времени отображает один цикл полной ротации сегментов, т.е. суммарное время однократного пребывания всей БД на одной рабочей станции. Цикл разбит на n равных отрезков времени длительностью T0. Это — такт системы, в течение которого каждая РС связана с одним сегментом БД. Время длительности такта T0 состоит из собственно времени Tдост
активного доступа к сегменту БД, пребывающему в данный момент в памяти РС, и времени ротации tрот, в течение которого производится смена сегмента в памяти РС с помощью сетевой ОС при невозможности доступа пользователя, T0 = Tдост + tрот. Таким образом, можно говорить о коэффициенте kдост доступности сегмента БД, определяющего долю времени длительности такта T0, в течение которого пользователь имеет доступ к сегменту, пребывающему в памяти РС, . То есть если наступает время ротации, а на обслуживании находился запрос, то обслуживание прерывается. Запрос ожидает следующего появления необходимого сегмента в памяти РС. Однако это может касаться лишь той стадии обслуживания запроса, при которой происходит непосредственное обращение к памяти, занимаемой сегментом, так как обработка запроса после такого обращения к памяти может быть продолжена и закончена одновременно с ротацией.
Рассмотренная схема в наибольшей степени соответствует ЛВС с организованным круговым одновременным обменом между рабочими станциями по принципу "соседу слева (справа)".
Заметим, что передача по принципу общей шины приводит к разделению времени обмена. Однако и в этом случае есть простой выход — в асинхронном пребывании сегментов в памяти РС. В этом случае ротация сегментов производится последовательно между парами РС по кругу, а каждый вновь поступивший на РС сегмент до удаления прежнего сегмента находится в специальном буфере.
Такая, с учетом работы общей шины, ротация представлена на рис. 2.2.


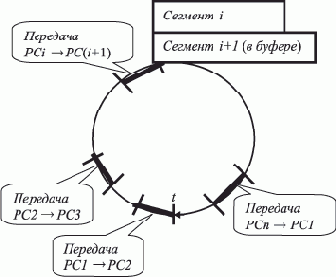
Рис. 2.2.  Ротация сегментов по общей шине

При этом необходим компромисс между временем последовательного обмена внутри каждой пары РС и длительностью T0 пребывания сегмента на отдельной РС. Так как T0 в ЛВС с "шинной архитектурой" может существенно возрасти, это, как будет видно далее, приведет к увеличению среднего времени ожидания сегментов на РС в случае поступления к ним запросов.

Обращаем внимание на то, что рассмотренные схемы ротации с последовательным доступом к каждому сегменту предполагают возможность выполнения таких запросов, по которым вносятся изменения в БД. Дополнительная синхронизация доступа к БД в этом случае не требуется.

Кольцевая схема ротации с сервером. Наличие сервера (рис. 2.3) в ЛВС при той же кольцевой схеме ротации, благодаря существенно большему объему памяти, позволяет значительно увеличить количество сегментов, "блуждающих" в сети, сделав их число независящим от числа рабочих станций.


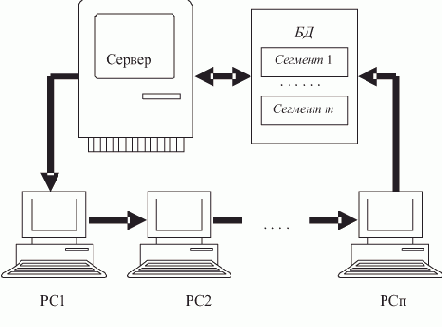
Рис. 2.3.  Ротационная БД с сервером

Кроме того, сервер позволяет разнообразить дисциплины ротации. Он допускает такое решение, при котором цикл ротации отдельных сегментов может изменяться, быть разным для разных сегментов, исключать сегменты из ротации вообще, организовывать архивы и т.д.

Ротационная БД в ЛВС типа "звезда". Работа БД представлена на рис. 2.4.


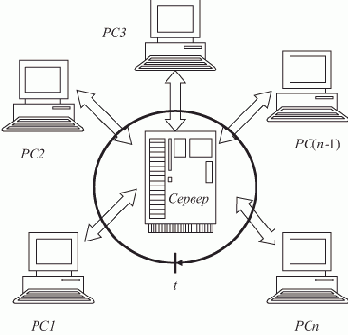
Рис. 2.4.  БД в ЛВС типа "звезда"

ЛВС типа "звезда" реализует все достоинства ранее рассмотренной ЛВС с сервером и позволяет их развить. Это развитие заключается в следующем.

Оперативно реализуется переменная структура ЛВС, так как рабочие станции легко могут исключаться "из обращения", а также могут включаться дополнительные станции.

ЛВС становится в большей степени управляемой. В частности, в процессе работы пользователя некоторые запросы могут приводить к длительному времени отсутствия новых запросов. Например, при работе с затребованной литературой, архивными материалами и т.д.На это время целесообразно исключить РС из процесса ротации, ускорив работу других РС. Такая возможность может быть учтена либо сервером, либо самим пользователем. В последнем случае он получает возможность "включаться" в БД, если ему это необходимо, либо "выключаться" из нее. Тем самым он увеличивает производительность своего компьютера.

Временной режим работы обусловлен периодическим обменом сегментами БД "сервер РС". А именно, сервер в интервале обмена забирает возможно измененный сегмент БД и сообщает ему новый. При этом для реализации последовательного доступа в случае изменения (записи новых) данных один сегмент БД в каждый момент времени может находиться не более чем на одной РС.

Эффективность и технические требования

В общем случае, при вхождении сервера в состав ЛВС и при разбиении БД на m сегментов, при котором m > n (n — число рабочих станций), вероятность нахождения сегмента на одной из РС в процессе ротации равна . Вероятность нахождения сегмента на конкретной РС равна .
Схема на рис. 2.3 соответствует случаю m = n.
Тогда среднее время Tож ожидания нужного сегмента, то есть возможного начала обращения к нужному сегменту на той РС, которая выработала запрос, находится на основе вероятности того, что он поступит через один такт, через два такта и т.д. Максимальное число учитываемых тактов равно m - 1:

(2.1)

Тогда полное время обслуживания запроса в ротационной БД находится следующим образом:

(2.2)

где tобсл — время выполнения запроса с помощью СУБД.
Сравним это полное время обслуживания со средним временем обслуживания T*обсл "традиционной" БД, реализованной на сервере. Напомним, что при обслуживании такой БД многоканальная система массового обслуживания, где множество рабочих станций обеспечивают массовый доступ, реально, с помощью одноканальной СУБД, на этапе обслуживания потока заявок преобразуется в одноканальную систему массового обслуживания с неограниченной очередью.
Допустив, что время выполнения запроса с помощью СУБД в данном случае совпадает с тем же временем в ротационной БД (ротация не предполагает каких-либо принципиальных изменений "традиционных", известных, широко применяемых СУБД), получим:

(2.3)

где ? — известное отношение , а ?* — суммарная интенсивность потока запросов со всех рабочих станций ЛВС, ? — интенсивность обслуживания, .
Уточним, что ?* = n?польз, где ?польз — интенсивность потока запросов с одной РС при данной организации БД. Однако здесь мы пренебрегли временем передачи сообщений в ЛВС, учитывая существенный характер ограничений другого рода. А именно, суммарная интенсивность ?* потока запросов в системе должна быть ограничена значением, обеспечивая соотношение ? < 1. Полное время обслуживания T*обсл значительно возрастает при значениях ?, близких единице:

T*обсл ?,

? 1.

В ротационной базе данных каждая РС независимо от других реализует одноканальную систему массового обслуживания с неограниченной очередью, где, несомненно, тоже должно выполняться соответствующее ограничение ?польз < ?польз, где ?польз — интенсивность запросов пользователя с одной РС, ?польз

— интенсивность обслуживания запросов пользователя с одной РС, Однако пользователь полностью управляет своими запросами, и случайный характер их поступления изучать нецелесообразно. Дисциплинированный пользователь формирует свои запросы последовательно, в диалоговом режиме, и не формирует новых запросов, не дождавшись ответа на предыдущие. Тогда приблизительно можно считать, что интенсивность потока запросов пользователя ограничена некоторыми возможностями системы, а именно

(2.4)

где ?max — некоторая максимально возможная интенсивность потока запросов, последовательно (по мере выполнения) формируемых пользователем в том случае, если доступ к сегментам базы данных, находящимся в памяти его РС, не ограничен ротацией, т.е. tрот = 0.

Таким образом, исследуя вопрос о целесообразности построения ротационной БД, необходимо изучить практические возможности обеспечения таких характеристик ЛВС, их аппаратных и программных средств, при которых выполняется соотношение

или

(2.5)

где



Напоминаем, что здесь

T0 — время (длина) такта системы,

m — число сегментов БД,

n — число рабочих станций ЛВС,

tобсл — время выполнения одного запроса СУБД (характеристика используемой системы управления базой данных),

?польз — интенсивность потока запросов одного пользователя,

? — интенсивность обслуживания запросов данной СУБД.

Однако выражение (2.5) получено в предположении, что заявка на обслуживание, поступившая от конкретной РС к некоторому сегменту si, не претерпевает какого-либо влияния возможных, в достаточно близкое время, заявок, пришедших к этому же сегменту от других РС "на пути следования" сегмента к данной РС. А именно, за предполагаемое среднее время Tож требуемый сегмент может быть "перехвачен" другой РС, "предшествующей" ожидающей.


При значительной интенсивности ? заявок такой возможностью нельзя пренебречь.

Предположим не более чем однократную возможность такого "перехвата".

Тогда, считая, что поток заявок к БД простейший (пуассоновский, экспоненциальный), вероятность Pi того, что сегмент si без дополнительных помех на пути следования дойдет до данной РС, находится как

(2.6)

Здесь ?i — суммарная интенсивность запросов к сегменту si за время Tож от среднего числа других пользователей, находящихся "на пути следования" этого сегмента.

Если запросы ко всем сегментам равновероятны, то

(2.7)

Тогда

(2.8)

При однократном "перехвате" его вероятность считаем равной 1-P.

"Перехват" дополняет общее время выполнения заявки составляющей (1-P)tобсл. Тогда окончательно среднее время обслуживания заявок в ротационной БД в рассматриваемом случае определяется как

(2.9)

Вместо выражения (2.5), с учетом (2.1), (2.8), (2.9), для обоснования ротации информации мы должны так подобрать параметры сети, сегментацию БД и временные параметры ротации, чтобы выполнялось (причем существенно!) соотношение

(2.10)

Многосерверные сетевые БД с циркулирующей информацией

Рассмотрим локальную вычислительную сеть, которая работает по принципу "клиент-сервер" при удовлетворении запросов от рабочих станций к сегментированной базе данных, находящейся на сервере.
Пусть ? — интенсивность интегрированного потока запросов, поступающего от всех РС, ? — интенсивность потока обслуживания.
Пусть, далее, в силу специфики применения все запросы — простые, т.е. реализуют обращение не более чем к одному сегменту БД каждый и при обслуживании одного запроса не возникает обращений к другим сегментам (что характерно для сложных запросов).
Данную схему функционирования БД можно интерпретировать одноканальной системой массового обслуживания (сервер выполняет функции СУБД) с бесконечной очередью.
Тогда среднее время T*обсл обслуживания одной заявки вычисляется следующим образом:

(2.19)

где tобсл = 1 / ? — "чистое" время выполнения работ по обслуживанию одной заявки с помощью СУБД, ? - ? / ?.
Разработчики сетевых БД традиционно не учитывают те параметры комплексирования сети, при которых дальнейшая нагрузка на БД (подключение новых РС) становится недопустимой. Ведь T*обсл ? при ? 1!
Выход из критического положения заключается в использовании не одного, а нескольких серверов, т.е. в переходе к модели многоканальной системы массового обслуживания.
Возможны различные схемы разделения нагрузки между серверами. Это — разделение сегментов БД между серверами при обеспечении связей всех РС с каждым сервером.
Другая схема может предполагать подключение групп РС к одному серверу при возможности использования одним сервером сегментов, расположенных на другом сервере. Такая схема приводит к появлению новых запросов в сети.
Возможна схема, при которой БД дублируется на каждом сервере. Тогда запросы, изменяющие состояние БД, должны "отслеживаться" на каждом сервере.
Все такие схемы затрудняют синхронизацию использования общих данных, усложняют работу СУБД.
Простой выход представляет организация движения, циркуляции сегментов БД между n серверами при подключении каждой РС к одному, "своему" серверу.
Время выполнения заявки при этом увеличивается лишь за счет времени ожидания прихода нужного сегмента на сервер.

Такая схема организации сетевой БД показана на рис. 2.7.


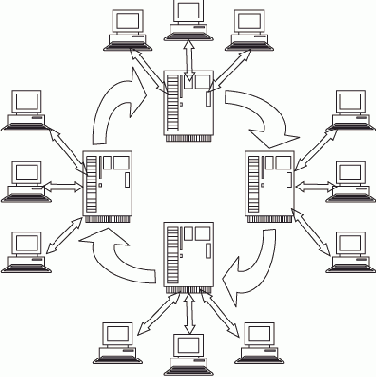
Рис. 2.7.  Многосерверная БД с циркулирующими сегментами

Если к каждому серверу подключено примерно одинаковое число k РС, то интегрированный поток запросов делится поровну между серверами, и интенсивность ?серв потока запросов к одному серверу можно считать равной ?/n.

Тогда время обслуживания одного запроса РС вычисляется следующим образом:

(2.20)

где t*обсл — "чистое" выполнение работ по обслуживанию, заключающее в себе издержки на организацию этого обслуживания, причем



Очевидно, что t*обсл = tобсл + tож. Значение tож обусловлено циркуляцией сегментов БД между серверами и без учета "перехвата" другими серверами на пути следования может быть оценено (см. (2.2)):

(2.21)

С учетом возможности единственного "перехвата" сегмента на пути его следования по (2.9) находим

(2.22)

где P отыскивается (см. (2.6)—(2.10)) как:

(2.23)

Здесь n — количество серверов, m — количество сегментов БД, интенсивность запросов пользователя ?польз = ?серв/k, T0 — длительность такта системы.

Тогда очевидно, что рассматриваемая организация сетевой базы данных имеет смысл, если Tобсл << T*обсл.

Отметим, что предлагаемые выше механизмы перемещения информации в сетевой БД, т.е. механизмы активизации ее совокупной памяти, отражают технический уровень построения БД, структуру, способ организации и способ использования памяти ЛВС. Над этим уровнем строится логическая и функциональная сущность БД, которая "не знает", как он устроен. В аналогичной ситуации разработчик программной системы (или транслятор) "не знает" (ибо не опирается на это), как реализуется идея виртуальной памяти компьютера, то есть, каковы механизмы замещения страниц, какова дисциплина замещения и т.д. Это — не его уровень.

В то же время, сегодня мы не можем с уверенностью опровергнуть сомнения в том, что применительно к БД удастся достичь полной независимости таких уровней. Громоздкость выкладок на основе вероятностных оценок, заведомо неполный учет всех факторов говорят, что в целом мы имеем дело с задачей детерминированного имитационного моделирования. Процесс должен быть воспроизведен как можно ближе к реальному, определяя натурный эксперимент. Это позволит оценить действительные возможности сетевого программного обеспечения и технические характеристики ЛВС.

Вместе с тем, здесь не предлагается новый, абсолютный способ организации хранения и использования информации в базах данных, отвергающий все то, что было разработано ранее. Цель настоящей публикации — показать, что существует способ сокращения времени обработки запросов к БД, основанный на организации "встречного" движения информации в ней. Этим способом можно пользоваться частично и весьма обоснованно, для чего предлагаются некоторые соотношения — критерии. Представленные же здесь схемы "рафинированно", по максимуму отражают предложения, но не навязывают каких-либо типовых структур данных.

В этом смысле арсенал средств повышения эффективности базы данных, которым располагает конструктор — разработчик БД, расширяется еще одним средством — средством активизации памяти для "встречного" предложения информации в сетевой базе данных, которым он может воспользоваться после тщательного обоснования. Можно предположить, что различные, прежде всего, по функциональному назначению, БД в разной степени допускают применение предложенного принципа. Например, можно надеяться на то, что встречное движение информации в вычислительной сети способно сократить длину очереди к билетным кассам на поезда дальнего следования.

Принцип работы БД с циркулирующей информацией

Рекомендации по организации вычислений неотделимы от модификации самих методов вычислений, традиционно продолжающих линию минимизации количества операций (привлекательной на уровне счетчиков—вычислителей, работающих с арифмометром или, в лучшем случае, с однопроцессорной ЭВМ 60-х годов). Распараллеливание выдвигает другой критерий эффективности: минимизация длины критического пути в информационно-логическом графе решаемой задачи или максимизация коэффициента загрузки исполнительных устройств системы.
Желание уйти от рекомендаций общего характера приводит к рассмотрению классов задач или отдельных "представительных" задач и к демонстрации их возможностей параллельного решения по SPMD-технологии, привлекающей все большее внимание как разработчиков ВС, так и математиков-программистов. По этой технологии вычислительный процесс организуется так, что единственная программа одновременно запускается на всех исполнительных устройствах — на процессорах ВС, на ЭВМ вычислительного комплекса, на рабочих станциях (РС) ЛВС. В этой программе — монопрограмме — "упрятаны" не только сама конфигурация алгоритма обработки, но и механизмы распределения данных, обрабатываемых по одному и тому же алгоритму, синхронизация исполнителей при обработке общих данных, возможность обработки данных по разным ветвям алгоритма (не путать с векторным способом обработки массивов!), универсальность монопрограммы, инвариантной относительно количества участвующих исполнителей и объемов обрабатываемой информации. При этом важно, что при организации совместных действий исполнительных устройств отсутствуют обращения к операционной системе.
Исследование возможностей применения SPMD-технологии к решению задач обработки баз данных приводит к необходимости превращения ее в систему с многоканальным доступом пользователей - в многоканальную систему массового обслуживания. Программно это выражается в том, что система управления базой данных (СУБД), как монопрограмма, должна быть "размножена" для независимого запуска на каждом исполнительном устройстве, непосредственно связанном с пользователем или участвующем в обработке интегрированного потока запросов пользователей (например, в многопроцессорном сервере).
Однако мы сталкиваемся с рядом трудностей, связанных с существованием "узкого горла", так характерного для обработки БД. Не говоря о технических возможностях носителей информации, во многих случаях допускающих последовательный доступ, следует учесть ряд функциональных особенностей БД, требующих оперативного изменения данных, синхронизации обращения к общим данным или к одним и тем же сегментам БД, а также обработки сложных запросов, динамически формирующих многократное обращение к БД. И все же, как максимально "расширить" это "узкое горло", снизив накладные расходы на доступ к информации и на синхронизацию обращений?

Предлагается способ преобразования централизованной сетевой базы данных из традиционно одноканальной в многоканальную систему массового обслуживания на основе применения SPMD-технологии. Способ заключается в организации встречного движения информации к пользователям, рабочие станции которых располагают копией системы управления базой данных. Целью рассматриваемых построений является минимизация времени обслуживания.

Очевидно, если мы хотим снабдить каждого пользователя своей СУБД, то необходимо обеспечить ему доступ на равных правах с другими пользователями. Это требование касается и БД, в силу своих функциональных особенностей допускающих лишь последовательный доступ. Например, доступ к БД — электронной исторической библиотеке, где информация при обращении не изменяется, является параллельным и независимым. Однако доступ к БД транспортного обслуживания является строго последовательным.

Следовательно, многоканальный доступ может быть реализован лишь тогда, когда организовано последовательное встречное предложение базы данных каждому пользователю. БД должна работать в режиме разделения времени.

Здесь мы реально наталкиваемся на "однобокость" развития методов обработки больших массивов информации. Совершенствуя алгоритмы обработки, мы предполагаем "статичность", "пассивность" системы памяти. Память (совокупная память всей системы) должна стать активной, способствовать процессу хотя бы на основе вероятностных предположений, должна реализовать встречные предложения, способные обеспечить снижение среднего времени выполнения запросов пользователей.


Такой способ активизации памяти, основанный не на покое БД, а на ее движении хотя бы внутри ЛВС, рассмотрим далее.

Мы отдаем предпочтение ЛВС и не исключаем другие применения, так как линии передачи данных, используемые в этих сетях, обладают наибольшим темпом развития, совершенствования, ростом пропускной способности. Именно их современные возможности в первую очередь вселяют надежду на реальность идеи активизации памяти, основанной на оперативном обмене данными.

Традиционно, базы данных, реализованные в ЛВС, делятся на централизованные и распределенные.

В централизованных БД вся информация размещается в памяти сервера. Запрос от каждой рабочей станции поступает на сервер и обрабатывается в порядке общей очереди поступивших заявок от всех РС. СУБД в этом случае является прибором обслуживания в одноканальной системе массового обслуживания с ограниченной или бесконечной очередью. Из практических соображений удобно считать очередь бесконечной.

Распределенная БД, при отсутствии сервера, предполагает разбиение информации на сегменты и их жесткое распределение между рабочими станциями. Такая БД воплощает идею многоканальной системы массового обслуживания, так как СУБД реализована на каждой РС и обслуживает запросы только с данной рабочей станции. Подобное воплощение, на практике обусловленное отсутствием возможностей использования мощного сервера, приводит к уверенности, что реализация многоканального доступа способна не только компенсировать этот недостаток, но и достичь большей пропускной способности БД.

Однако ряд сложностей затрудняет реализацию указанных БД, существенно увеличивая время обслуживания запроса. Эти сложности обусловлены:

необходимостью определения места расположения требуемого сегмента БД;

организацией его пересылки в память данной РС (один вариант обслуживания);

организацией переадресации запроса к СУБД той рабочей станции, на которой находится требуемый сегмент (другой вариант обслуживания);

организацией выдачи результата выполнения запроса на ту РС, где этот запрос был сформирован;

синхронизацией множественных обращений к одним и тем же сегментам в случае изменения информации в результате выполнения запросов (например, в системах транспортного обслуживания).

Синхронизация множественных обращений к сегментам БД в случае изменения информации требует применения аналога механизма семафоров с его весьма сложными процедурами, обеспечивающими, например, решение таких типовых задач синхронизации, как задача "взаимного исключения" или "читатели — писатели".

Развитие сетевых технологий и, в частности, рост характеристик средств обмена информацией, на новом уровне выдвигают задачи поиска компромиссных, промежуточных архитектур сетевых БД, воплощающих в себе как идею многоканального доступа, так и синхронизацию производимых изменений информации. Такие БД должны обладать высокой оперативностью, где под этим понимается минимизация среднего времени обслуживания запроса.

Основная идея, предлагаемая в настоящей работе, заключается в активизации совокупной памяти ЛВС, в которой располагается БД. Разбитая на сегменты БД предлагает встречный обмен, встречное предложение своих сегментов рабочим станциям, реализуя различные дисциплины таких предложений. Таким образом, сегменты БД циркулируют среди рабочих станций ЛВС. Такие сетевые БД, в которых производится ротация сегментов, находящихся в памяти каждой РС, назовем ротационными.

В этом случае запрос, сформированный пользователем на рабочей станции, ожидает момента поступления необходимого сегмента в память данной рабочей станции. СУБД данной станции, работая в "традиционном" одноканальном режиме обслуживания, выполняет запрос, вводя, если необходимо, изменения в сегмент. Далее, измененный уже сегмент продолжает маршрут своего перемещения. Развивая этот принцип, следует согласиться с тем, что дисциплина перемещения сегментов должна существенно зависеть от интенсивности обращений к конкретным сегментам. Например, некоторые сегменты, относящиеся к архивным, могут не участвовать в циркуляции. В циркуляции сегментов могут временно не участвовать и некоторые рабочие станции, если интенсивность запросов с этих станций резко снижается. Например, студент затребовал учебное пособие, с которым проработает несколько часов.На это время он вправе отключить себя от системы циркуляции БД, дополнительно загружающей ("тормозящей") компьютер. При необходимости он сможет подключиться вновь.

Сетевые базы данных с циркулирующими запросами-предложениями

Рассматриваемым ниже базам данных соответствует архитектура ЛВС с сервером типа "звезда" (рис. 2.5).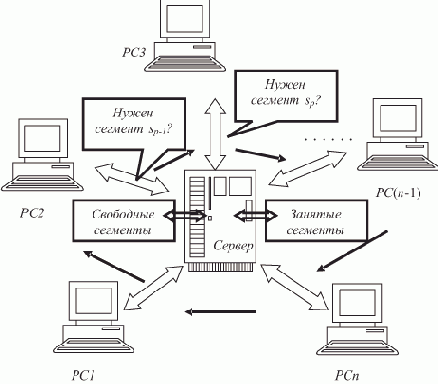

Рис. 2.5.  База данных с циркуляцией запросов-предложений
Пусть централизованная БД, расположенная на сервере, содержит список свободных сегментов, которые не обрабатываются в данный момент ни одной РС, а также список занятых сегментов, т.е. обрабатываемых рабочими станциями. Не рассматривая сложные запросы либо предполагая их структурирование, требующее последовательного обращения к разным сегментам, допустим, что одна РС может обрабатывать одновременно лишь один сегмент. Таким образом, количество занятых сегментов совпадает с количеством РС, занятых их обработкой.
Располагая списком свободных сегментов, сервер последовательно и циклически опрашивает свободные, т.е. не обрабатывающие ни один сегмент, РС с запросом- предложением: нужен ли ей очередной сегмент из этого списка? Подготавливая запрос, сервер максимально обеспечивает связь с РС для передачи сегмента в случае его необходимости, т.е. производит маршрутизацию.
Если пользователь сформировал запрос к БД со своей РС, то запрос (а по нему определяется необходимый сегмент БД) ожидает прихода запроса-предложения сервера относительно нужного сегмента. Тогда сервер направляет сегмент (точнее, его копию) на РС и этот сегмент переходит в список занятых.
Рабочая станция, закончившая обработку запроса к БД, возвращает в общем случае измененный сегмент серверу. Сегмент переходит в список свободных и впредь участвует в циклическом предложении свободным РС.
Таким образом, время выполнения каждого запроса к БД зависит от состояния сегмента (свободен — занят), от среднего времени обработки сегмента используемой СУБД, от времени одного цикла циркуляции запросов-предложений, от организации и подготовки обмена информацией (маршрутизации) в сети и т.д.
Отметим важность средств обеспечения надежности, защиты данных, отображения и др.
Рассчитаем среднее время обслуживания запроса при рассматриваемой организации его обработки.

Пусть, как и прежде, m — количество сегментов БД, n — количество РС в ЛВС. Для поиска вероятности того, свободен ли требуемый сегмент или взят на обработку (занят), необходимо определить в стационарном режиме среднее число занятых сегментов БД.

Считая поток запросов простейшим, построим цепь Маркова (рис. 2.6), соответствующую многоканальной системе массового обслуживания с количеством n каналов [17].


Рис. 2.6.  Цепь Маркова для нахождения предельных вероятностей состояния сегментов БД

Состояние S0 соответствует отсутствию занятых сегментов, поток запросов при этом реализуется полностью, т.е. ?0 = n ?польз. На обратный переход в это состояние влияет поток обслуживания с интенсивностью ?, формируемый копией СУБД единственной РС. Состояние S1 соответствует наличию одного занятого сегмента. Так как одна РС оказывается занятой обработкой сегмента, то поток запросов к БД реализуется n - 1 свободными. Кроме того, из этого потока исключаются запросы к занятому сегменту. Тогда . Поток обслуживания, приводящий в это состояние из состояния S2, характеризующегося двумя занятыми сегментами, определяется двумя копиями СУБД. Интенсивность этого потока обслуживания равна 2? и т.д.

Таким образом, для состояния Si, i = 0 , ..., n, когда занято i сегментов,

(2.11)

а интенсивность потока обслуживания (для i < n), приводящего в это состояние, равна (i + 1)?.

Уравнения Колмогорова имеют вид

(2.12)

Решая [17] эту систему, находим:

(2.13)

Определим среднее число q занятых сегментов:

(2.14)

Тогда вероятность обращения к занятому сегменту

(2.15)

Пусть tпредл — цикл времени предъявления очередной заявки-предложения рабочей станции. Тогда среднее время ожидания свободного сегмента вычисляется следующим образом:

tожид своб. = 0,5 (m - q) tпредл. (2.16)

Если сегмент, к которому произведен запрос, занят, то время tожид. зан. его ожидания зависит от времени окончания его обработки, от времени tвозвр возврата серверу, от времени tосвоб включения в число свободных и от времени его ожидания как свободного сегмента:

tожид.зан. = 0,5 tобсл. + tвозвр. + tосвоб. + tожид своб. (2.17)

Тогда полное время обслуживания запроса с РС вычисляется:

Tобсл = Pзанят tожид.зан + (1 - Pзанят)tожид своб + tобсл. (2.18)

Полученная оценка, аналогично (2.5) и (2.10), является основой критерия эффективности данного способа организации сетевой БД.

Параллельное программирование

Анализ сетевых топологий и обоснование

В связи с распространением персональных компьютеров и созданием на их основе автоматизированных рабочих мест (АРМ) возросло значение локальных вычислительных сетей (ЛВС). Правильно организованная и умело эксплуатируемая сеть обеспечивает целый ряд преимуществ по сравнению с отдельным компьютером.

Распределение данных (Data Sharing). Данные в сети хранятся на центральном РС и могут быть доступны для любого РС, подключенного к сети, поэтому не надо на каждом рабочем месте хранить одну и ту же информацию.

Распределение ресурсов (Resource Sharing). Периферийные устройства могут быть доступны для всех пользователей сети, например: принтер, факс-модем, сканер, диски, выход в глобальную сеть.

Распределение программ (Software Sharing). Все пользователи сети могут иметь доступ к программам, которые были один раз централизованно установлены.

Электронная почта (Electronic Mail). Все пользователи сети могут передавать и принимать сообщения.

Обеспечение широкого диапазона решаемых задач, предъявляющих повышенные требования к производительности и объему памяти.

Локальные сети имеют некоторые особенности.
Главная из них — это связь. Она должна быть быстрой, надежной и удобной. Обычно, локальные сети не выходят за пределы нескольких комнат или одного здания, поэтому длина линии связи обычно не превышает нескольких сотен метров. Они связывают между собой ограниченное количество РС. Все это позволяет обеспечить качественную связь. Поэтому скорость передачи данных обычно составляет от 10 Мбит/с и выше. К тому же, требуется надежная связь, иначе при исправлении ошибок теряется выигрыш в скорости. Также необходимо небольшое время ожидания установления связи, так как оно включено в общее время передачи информации. При таких высоких требованиях в локальных сетях используются специальные технические средства.
При построении сетей ЭВМ, в т.ч. локальных, говорят о их топологии.
Топология — описание способа, при помощи которого рабочие станции и серверы физически соединяются между собой. Топологии различаются требуемой длиной соединительного кабеля, удобством соединения, возможностями подключения дополнительных абонентов, отказоустойчивостью, возможностями управления обменом. Топологическая структура влияет на пропускную способность и стоимость локальной сети. Каждая топология сети налагает ряд условий. Например, она может диктовать не только тип кабеля, но и способ его прокладки. Отличительной особенностью ЛВС является наличие моноканала, т.е. единственного маршрута, связывающего любые две станции. В связи с этим при подключении устройств к сети используются три топологии.

Кольцевая сеть FDDI, IBM Token Ring)

"Кольцо" — последовательное соединение абонентов в замкнутое кольцо (рис. 3.2), что и определяет его особенности. Во-первых, вся передаваемая информация проходит через всех абонентов. Поэтому выход из строя любого из них нарушает работу всей сети в целом. Во-вторых, разрыв кабеля в любой точке нарушает целостность кольца и выводит из строя всю сеть. Для этого применяют дублирование кабеля. Управление может быть как централизованным, так и децентрализованным, оно не так жестко зависит от топологии, как в случае "звезды". Все адаптеры должны быть одинаковы, но иногда один из них выполняет функции диспетчера сети, тогда он значительно сложнее.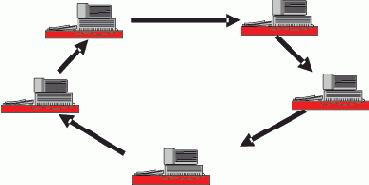

Рис. 3.2.  "Кольцевая" сеть
Эта топология допускает большое число абонентов, причем возможно изменение их количества. В кольце происходит автоматическое усиление передаваемого сигнала каждым абонентом, поэтому его размеры могут быть очень большими, и ограничены они только временем прохождения сигнала по всему кольцу.

Концепция построения вычислительных комплексов на базе локальной вычислительной сети

Технический прогресс, несомненно, сказывается на увеличении частоты работы элементной базы, на повышении степени интеграции, но технический же прогресс приводит к появлению все новых задач, требующих еще более значительного роста производительности вычислительных средств. Это можно считать законом, приводящим к новым уловкам при совмещении работы устройств ВС, при увеличении их количества в системе, при увеличении их эффективности в процессе решения задач.
Под эффективностью работы устройства в составе ВС или компьютера в составе ВК понимают степень его участия в общей работе ВС или ВК при решении конкретной задачи — коэффициент загрузки устройства (компьютера). Распараллеливание работ оправдано, если приводит к существенному росту усредненного по всем устройствам (компьютерам) коэффициента загрузки оборудования при решении задач. Это непосредственно сказывается на времени решения. Сегодня говорят не о специальном классе задач, а о задачах, ориентирующих ВС и ВК на универсальность, что обусловлено современными областями применения.
Важным революционизирующим моментом стал переход на микропроцессорную элементную базу, обусловившую построение мультимикропроцессорных ВС для параллельной обработки информации или компьютерных сетей для распределенной обработки информации.
Основная сложность распараллеливания заключается в соблюдении частичной упорядоченности распределяемых работ. Поэтому решение задач синхронизации параллельного вычислительного процесса в ВС или распределенного вычислительного процесса в ВК сопровождает все усилия по организации совместной работы устройств. Организация распределенного вычислительного процесса предъявляет повышенные требования к скорости синхронизирующего взаимного обмена данными, что и послужило сдерживающим фактором применения ВК.
Необходимость оперативного решения сложных задач стимулирует усилия по разработке дорогих и уникальных супер-ЭВМ. Однако на новом витке развития все более привлекательной становится идея возврата к использованию коллектива компьютеров, совместно решающих общую задачу, — идея построения ВК для распределенной обработки информации.
Эта идея связана с развитием сетевых технологий, достигших такого уровня, когда оперативность взаимодействия компьютеров в сети позволяет расширить применение сетей. Построение ВК на основе компьютерной сети (в пространстве компьютерной сети) должно привлечь своей естественностью, достаточностью аппаратных и программных средств, не требующих дополнительных разработок, непреложным развитием сетей вне зависимости от данного применения.

Сетью ЭВМ называется комплекс территориально рассредоточенных ЭВМ и терминальных устройств, связанных каналами передачи данных.

Сейчас сложилась такая практика, что с сетями ЭВМ связывают более общее понятие — информационная система. Однако изначально целью создания сетей ЭВМ было:

Совместное использование суммарных вычислительных ресурсов. (Данная цель характерна на ранней стадии распространения сетей. Когда-то восторг вызывало то, что задача, введенная в Нью-Йорке, в действительности решалась в Париже — в соответствии с наличием вычислительных ресурсов.)

Обеспечение широкого диапазона решаемых задач, предъявляющих повышенные требования к производительности и объему памяти. (На возможность распараллеливания возлагались также надежды на этапе разработки первых сетей ЭВМ. Однако возврат к этой идее наблюдается сейчас: в распределенных вычислительных комплексах, используемых в системах управления, в том числе — бортовых, все настойчивее изыскиваются возможности применения сетевых технологий, весьма продвинутых в направлении стандартизованного оперативного обмена.)

Обеспечение высокой надежности систем обработки информации (за счет возможности перераспределения выделяемых ресурсов).

Совместное и взаимное информационное обслуживание, расширение сети пользователей ЭВМ, развитие качественно новых средств коммуникаций. (Обмен данными и совместное использование централизованных или распределенных банков данных.)

Социальный прогресс, обусловленный культурным, научным, деловым обменом, общедоступностью информации наряду с возможностями адресной передачи. (Качественно новый уровень достигнут в культурном обмене, в дистанционном обучении, в проведении научных конференций, в демонстрационном показе и рекламе, в деловых контактах, в оперативности передачи значительных объемов данных по Еmail электронной почте и т.д.)

Таким образом, все большую актуальность обретает задача расширения возможностей сетей ЭВМ за счет возложения на них функций распределенных вычислительных комплексов для решения задач высокой сложности. На первом этапе речь может идти о локальных сетях (ЛВС), обладающих наиболее оперативным обменом. По-видимому, рано говорить о массовом применении сетей для решения задач управления в реальном масштабе времени, здесь требуемая оперативность обмена может быть не достигнута на уровне современных сетевых технологий. Однако в рамках современных представлений о сложности алгоритмов (например, о NP-сложных задачах) накладные расходы на обмен информацией в сети могут быть ничтожны по сравнению с общим временем решения задачи, обусловленным, в частности, применением методов перебора.

Чтобы избежать здесь голословных лозунгов, необходимо создавать и накапливать опыт решения сложных задач в компьютерных сетях. Такой подход позволит выявить и сформировать технологию подготовки и программирования подобных задач, поможет сформулировать требования к развитию аппаратных, программных и языковых средств, покажет область эффективного применения сетевых технологий решения задач.

Сказанное выше тем более важно сейчас, когда умы охватывает идея Grid-технологий — технологий предоставления сетью (включая Интернет) виртуальных ресурсов по запросам на решение сложных вычислительных задач.

Локальная сеть Ethernet

В настоящее время разными фирмами разработаны стандарты ЛВС, поддержанные аппаратно и программно. Наиболее распространенным стандартом, соответствующим требованиям режима вычислительного комплекса, является локальная сеть ETHERNET. (Спецификацию разработали компании Xerox Corporation, Digital Equipment Cjrporation (DEC), Intel Corporation.)
На базе Ethernet разработан стандарт IEEE 802.3. Сеть предполагает несколько конфигураций. Использует коаксиальный или оптоволоконный кабель.
Применяется топология "шина", т.е.:

все устройства, подключенные к сети, равноправны, т.е. любая станция может начать передачу в любой момент времени, если передающая среда свободна;

данные, передаваемые одной станцией, доступны всем станциям сети.

Для организации взаимодействия станций в сети используется метод Множественного Доступа с Контролем Несущей и Обнаружением Столкновений (МДКН/ОС) — Carrier Sense Multiple Access / Collision Detection (CSMA/CD).
Контроль Несущей: во время работы станция постоянно проверяет среду передачи. Передающая среда может быть

свободна, т.е. ни одна другая станция не передает данные;

занята, т.е. идет передача данных другой станцией.

Множественный Доступ: при использовании метода любая станция, обнаружив, что среда свободна, может начать передачу своих данных. Поэтому возможна ситуация, когда одновременно несколько станций начнут передавать данные.
Обнаружение Столкновений (Коллизий): станция, обнаружившая коллизию, выдает другим станциям специальный сигнал, по которому переданная информация считается недостоверной. После этого каждая станция делает повторную попытку передачи через специально найденное ею случайное время. Разное для всех станций случайное смещение времени повторной передачи служит высокой вероятности избежания коллизии. (Оригинальный способ избежать централизованного управления!) Если за 16 попыток станция не смогла передать пакет, считается, что среда неисправна. В локальную сеть всегда входит несколько абонентов, и каждый из них в любой момент времени может обратиться к сети. Поэтому требуется управление обменом с целью упорядочения использования сети различными абонентами, предотвращение или разрешение конфликтов между ними. В противном случае возможно искажение передаваемой информации. Для управления обменом (или управлением доступом к сети, или арбитража сети) используются различные методы, особенности которых определяются выбранной топологией сети.

Организация параллельного решения задачи в локальной сети

Распараллеливание метода "сеток" с очевидностью адекватно второму способу распараллеливания, что и должно определить направление поиска. То есть можно с уверенностью заявить, что распределение узлов сетки между процессорами ВС (распараллеливание по информации), ЭВМ вычислительного комплекса или рабочих станций сети является эффективным способом параллельного решения системы дифференциальных уравнений в конечных разностях.
В лекции 1 рассматривался пример решения уравнения в частных производных. Далее на этом примере будут показаны схемы возможной реализации метода сеток в ЛВС.
По рис. 1.12 из курса "Архитектура параллельных вычислительных систем" мы можем полностью представить различные планы параллельного решения рассмотренной задачи.
Метод матричных вычислений характерен для матричных вычислительных систем. В таких системах организуются "быстрые" связи между процессорами в соответствии с преимущественными направлениями обменов информацией. Обычно это связи по строке и по столбцу с соединением "последнего с первым". Матрица процессоров "накладывается" на множество узлов сетки, воспроизводящее такую же матрицу, и узлы обрабатываются. Матрица процессоров циклически обходит матрицы узлов сетки.
Другая стратегия распределения узлов между процессорами может быть основана на делении области задания функции между процессорами. Т.е. вся область D на рис. 1.12 из курса "Архитектура параллельных вычислительных систем" может быть разделена поровну между процессорами ВС или станциями сети.
Третья стратегия может предусматривать нумерацию процессоров, превращение многомерного (в примере — двумерного) массива узлов сетки в одномерный линейный и назначение каждого узла на процессор с номером, равным остатку от деления его номера на число используемых процессоров. Эта стратегия, в наибольшей степени обеспечивающая инвариантность программы счета относительно числа узлов и числа используемых процессоров, соответствует рассмотренной ранее SPMD-технологии.
Равноправие процессоров (симметричность) делают целесообразным использование шинной архитектуры ЛВС. (Отметим, что на ранней стадии построения вычислительных комплексов применялась именно шинная архитектура, как наиболее простая и естественная. То же можно отметить и относительно многих современных и перспективных мультимикропроцессорных систем.) Распространенным стандартом такой архитектуры, обусловившим разработку широкой номенклатуры аппаратных средств, является сеть ETHERNET. Параллельный вычислительный процесс должен воспроизводить технологию SPMD, основанную на применении способа распараллеливания по информации.
Тогда организация параллельной обработки информации и схема вычислений должна быть следующей.

Исследуется задача и выделяется основной массив данных (одномерный или многомерный), обработку которого целесообразно распределить между станциями ЛВС, — опорный массив.

Формируется план распределения элементов опорного массива для обработки станциями сети. Разнообразие таких планов порождает и разнообразие возможных способов переадресации. Например, весь опорный массив может быть поровну (со следующими подряд элементами) поделен между станциями. Такой способ может применяться в случае, если длина массива не изменяется динамически. Более универсален способ распределения элементов опорного массива, когда после "расчета по n" каждый из них оказывается закрепленным за станцией с тем же номером. Это в точности соответствует технологии SPMD и поддержано системой команд. Такое распределение допускает динамическое изменение длин массивов (поддерживает динамический тип данных), что крайне важно при обработке баз знаний.

Составляется единственная для всех станций (предполагается их программная совместимость), универсальная программа циклической обработки элементов опорного массива, закрепленных за одной станцией. Программа должна содержать критический интервал обмена данными между станциями в необходимых (по алгоритму) направлениях. При этом запрос с последующим ожиданием данных (принцип редукционных вычислительных систем) должен отсутствовать, данные должны только отправляться. Это значит, что программы должны "уметь" ждать необходимые для себя данные. Поэтому становится целесообразным воспроизведение принципа data flow с помощью "почтовых ящиков".

Составляется программа ввода, визуализации и управления вычислительным процессом для станции (персонального компьютера), который назначается мониторным.

Задача решается в диалоговом режиме. Дело в том, что при большом времени собственно решения вмешательство пользователя (оператора) может быть не только неизбежным, но и желательным. Например, нахождение всех экстремумов функции можно автоматизировать следующим образом: разделить область задания функции между компьютерами и поручить им полностью исследовать свои подобласти; затем заставить их совместно исследовать полученные результаты и выделить глобальные экстремумы и др. Вторая задача может оказаться существенно сложнее. В то же время оператором она может быть решена значительно проще при достаточной визуализации. Принятое им решение может быть немедленно использовано при последующем автоматическом решении этой или другой задачи.

Рассмотрим конкретный возможный план решения рассмотренной выше задачи методом "сеток". Для простоты положим число используемых процессоров равным 2. В основу плана положим способ разделения области D между процессорами поровну. Зафиксируем hx = hy = h, определив тем самым количество узлов сетки в каждой строке и в каждом столбце. На рисунке 3.6 отражены выбранные количества узлов в строках и столбцах. Первая и последняя строка, как и первый и последний столбец, соответствуют узлам, в которых заданы граничные значения функции-решения.

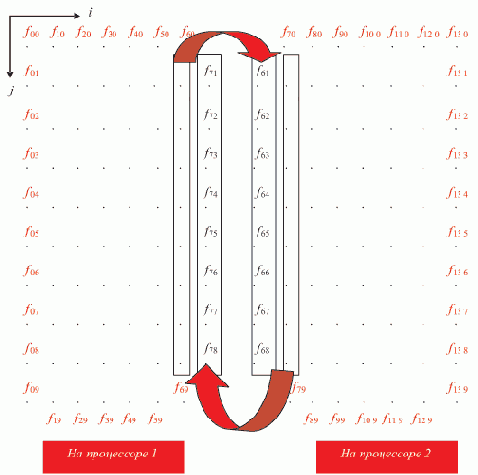
Рис. 3.6.  Распределение данных между двумя процессорами для решения задачи методом "сеток"
Область D1, обрабатываемая процессором 1, определяется границами индекса i и координаты x:
Область D2, обрабатываемая процессором 2, определяется границами индекса i и координаты x:
По второй координате 0 y t (m - 1)h = B.
На рисунке показана передача промежуточных значений узлов процессором процессору для счета узлов, использующих эти значения. Такая передача может осуществляться либо непосредственно после нахождения очередного приближения значения функции в узле, либо после очередной итерации — для всех необходимых значений сразу. Второй способ может значительно сократить время выполнения обмена, хотя задерживает использование узлов.
Важен выбор способа нахождения начального значения функции — решения в узлах. Этот выбор влияет на скорость сходимости решения.
В соответствии с граничными условиями
fi0 = f1(ih,0) i = 0, ..., n - 1,
fi,m-1 = f2(ih,(m-1)h=B) i = 0, ..., n - 1,
f0j = f3(0,jh) j = 0, ..., m - 1,
fn-1,j = f4((n-1)h=A,j) j = 0, ..., m - 1.
Нулевое приближение значений fij может быть рассчитано по формулам интерполяции с усреднением:
для всех 0 < i < A, 0 < j < B.
Итерационная формула имеет общий вид fij = F(fi-1,j, fi+1,j, fi,j-1, fi,j+1).

Шинная организация (Ethernet, ARCnet)

"Шина" — ориентирована на полное равноправие всех абонентов и идентичность их адаптеров (рис. 3.3). Это не означает, что управление обменом не может быть централизованным. Однако центр будет заниматься только управлением обменом, а не перераспределением информации. "Шина" может логически работать как "звезда" или "кольцо". "Шина", в отличие от других топологий, сильно зависит от электрического согласования используемых линий связи, потому что при любом повреждении кабеля возникают отражения и наложения сигналов. В таком случае нарушается работа всей сети. Однако, к выходу из строя компьютеров данная топология не чувствительна, нарушается обмен только с поврежденным компьютером, а вся остальная сеть остается в рабочем состоянии. Максимально допустимое количество абонентов в "шине" такое же, как и в "кольце". В "шине" легко менять количество подключенных абонентов, иногда даже в процессе работы. В связи со сложностью децентрализованного обмена, сложность аппаратуры в адаптерах выше, чем в других топологиях. Однако децентрализованное управление гораздо надежнее централизованного и лучше приспосабливается к изменяющимся внешним условиям.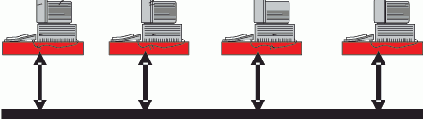

Рис. 3.3.  Сеть с общей шиной
Существуют также смешанные топологии, такие как "звезда-шина", "звезда-кольцо", которые имеют свои преимущества.

Таблица 3.2. Сравнение топологий сетейПараметрыЗвездаКольцоШина1. Отказоустойчивость2. Количество абонентов3. Изменение количества абонентов4. Влияние на общую стоимость сети5. Возможность управления обменом6. Особенности7. Протяженность8. Применение

Выход из строя одного PC не влияет на работоспособность сети	Выход из строя одного PC может вывести из строя всю сеть	Выход из строя кабеля останавливает работу многих пользователей
16	1024 и выше	1024 и выше
Возможно	Требует остановки всей сети	Легко изменяется
Дополнительные затраты на центральный компьютер	Дополнительные затраты на адаптер, выполняющий функции диспетчера сети	Дешевая среда передачи
Централизованное	Централизованное и децентрализованное	Децентрализованное
Мощность всей сети зависит от сервера	Количество пользователей не оказывает сильного влияния на производительность. Трудно локализовать проблемы	Оптоволоконные кабели не применяются. При значительных объёмах трафика уменьшается пропускная способность. Трудно локализовать проблемы.
	До нескольких десятков километров
В зависимости от предъявляемых требований

Для организации распределенных вычислений необходимо выбрать такую топологию сети, которая поддерживает равноправную, "симметричную" связь "каждый с каждым". Среди рассмотренных топологий таким требованиям в максимальной степени соответствует шинная архитектура. Преимущества этой архитектуры отображены исторически при практическом объединении ЭВМ в распределенные вычислительные комплексы для совместного решения сложных задач.

Сложность алгоритма и проблема распараллеливания

Ранее уже использовалось понятие сложности. Рассмотрим его полнее.
Пусть задан некоторый алгоритм A. Почти всегда существует параметр n, характеризующий объем его данных. Пусть функция T(n) — время выполнения A, а f — некоторая функция от n. Говорят, что алгоритм A имеет теоретическую (асимптотическую) сложность O(f(n)), если
,
где k — действительное.
Если алгоритм выполняется за фиксированное время, не зависящее от размера задачи, говорят, что его сложность равна O(1).
Это определение обобщается в случае, если время выполнения существенно зависит от нескольких параметров. Например, алгоритм, определяющий, входит ли множество m элементов в множество n элементов, может иметь, в зависимости от используемых структур данных, сложность O (m n) или O (m+n).
Практически время выполнения алгоритма может зависеть от значений данных. Так, время выполнения некоторых алгоритмов сортировки существенно сокращается, если первоначально эти данные были частично упорядочены. Чтобы учитывать это, сохраняя возможность анализировать алгоритм независимо от их данных, различают:

максимальную сложность, определяемую значением Tmax(n) — время выполнения алгоритма, когда выбранный набор n данных порождает наиболее долгое время выполнения алгоритма;

среднюю сложность, определяемую значением Tср(n) — средним временем выполнения алгоритма, примененного к n произвольным данным.

Эти понятия без труда распространяются на измерение сложности в единицах объема памяти: можно говорить о средней и максимальной пространственной сложности.
Самыми лучшими являются линейные алгоритмы, имеющие сложность порядка an=b. Они называются также алгоритмами порядка O(n) где n — размерность входных данных. Такие алгоритмы действительно существуют. Например, сложение двух чисел столбиком в случае, если одно из них состоит из n, а другое — из m цифр, требует не более max(n, m) сложений и не более max(n, m) запоминаний. Т.е. данный алгоритм имеет сложность порядка O(n+m). Разумеется, это выражение показывает только порядок величины — постоянные факторы в нем не учитываются.

Обобщение линейности дает нам первый большой класс алгоритмов — полиномиальных.

Полиномиальным (или алгоритмом полиномиальной временной сложности) называется алгоритм, у которого временная сложность есть O(p(n)), где p(n) — полином от n. Задачи, где для решения известен алгоритм, сложность которого составляет полином заданной, постоянной и не зависящей от размерности входной величины n степени, называют "хорошими" и относят их к классу P.

Экспоненциальной по природе считается задача сложностью не менее порядка xn, где x — константа или полином от n. Например, это задачи, в которых возможное число ответов уже экспоненциально. В частности, к ним относятся задачи, где требуется построить все подмножества заданного множества или все поддеревья заданного графа. Экспоненциальные задачи относят к классу E.

Соответственно, и алгоритмы, в оценку сложности которых n входит в показатель степени, относятся к экспоненциальным.

Необходимо отметить, что при небольших значениях n экспоненциальный алгоритм может быть даже менее сложным, чем полиномиальный. Тем не менее, различие между этими типами алгоритмов весьма велико и проявляется при больших значениях n.

Особую группу по значениям сложности, близким к полиномиальным, составляют алгоритмы, сложность которых является полиномиальной функцией от log n (поскольку log n растет медленнее, чем n).

Для большей убедительности и сравнения полиномиальных и экспоненциальных алгоритмов приведем таблицу, где единица времени — 1 мкс, а сложность совпадает с необходимым количеством единиц времени для обработки набора n данных:

Таблица 3.1. Сложность и время выполненияСложностьРазмер задачи — n102030405060nn?n?n52n3n

0.00001 с	0.00002 с	0.00003 с	0.00004 с	0.00005 с	0.00006 с
0.0001 с	0.0004 с	0.0009 с	0.0016 с	0.0025 с	0.0036 с
0.001 с	0.008 с	0.027 с	0.064 с	0.125 с	0.216 с
0.1 с	3.2 с	24.3 с	1.7 мин	5.2 мин	13.0 мин
0.01 с	1.0 с	17.9 мин	12.7 дней	35.7 лет	366 веков
0.59 с	58 мин	6.5 лет	3855 веков	2·108 веков	1.3·1013 веков

Приведенная таблица иллюстрирует причины, по которым полиномиальные алгоритмы считаются более предпочтительными, чем экспоненциальные.

Уточним понятие сложности для итеративных и рекурсивных алгоритмов.

Отнесем к итеративным алгоритмам и те, к которым сводятся рекурсивные алгоритмы (например, вычисление факториала n!). Тогда время их выполнения (в случае сходящегося процесса) зависит от главного условия повторения итерации, например, от требуемой точности. Если мы установим время или сложность одной итерации, то сможем умножением на число итераций установить максимальную или среднюю сложность. Число итераций устанавливается теоретически или экспериментально. Например, так можно сделать при расчете значений функций по их разложению в ряд.

Однако иногда приходится решать оптимизационную задачу, выбирая между сложностью одной итерации и количеством итераций.

Для большинства конечно-разностных схем решения дифференциальных уравнений методом сеток можно считать, что сложность одной итерации составляет O(n2) или O(n ? m), где n2 — количество узлов при равном разбиении по x и по y, а n? m — то же количество при различающемся разбиении по осям. Увеличение количества узлов, покрывающих ту же область, т.е. уменьшение hx и hy, увеличивает скорость сходимости - и, соответственно, уменьшает число итераций, но сложность каждой итерации растет квадратично. Значит, необходим компромисс, который достигается посредством изучения поведения процесса, как на теоретическом, так и на экспериментальном уровне, вплоть до автоматической коррекции шагов в процессе вычислений в зависимости от локального поведения аппроксимаций производных. Т.е. шаги становятся непостоянными во всей области.

Однако по своей природе действительно рекурсивные алгоритмы по сложности относятся к классу экспоненциальных алгоритмов. Как правило, это задачи оптимизации, основанные на переборе (алгоритмы с возвратом, метод "ветвей и границ").

Имеется широко распространенное соглашение, по которому задача не считается "хорошо решаемой", пока для нее не получен полиномиальный алгоритм.


Задача называется труднорешаемой, если для ее решения не существует полиномиального алгоритма.

Эта градация относительна, ибо сложность определяется по наихудшему варианту. Хотя реализация метода "ветвей и границ" — труднорешаемая задача (при теоретической оценке по максимальной сложности), сейчас для многих задач известны такие алгоритмы, которые практически очень быстро находят решение именно методом ветвей и границ.

Однако есть понятие гарантированных и негарантированных оценок. Если сложность задачи полиномиальная, мы можем уверенно предсказать оценку времени решения. При решении задачи методом "ветвей и границ" незначительное изменение начальных данных даже без изменения размерности задачи может непредсказуемо привести к резкому скачку в увеличении времени решения. Т.е. существует большой разрыв между значениями теоретической максимальной сложности и практической средней сложности экспоненциальных алгоритмов. Постоянно ведутся поиски более эффективных экспоненциальных алгоритмов.

Полиномиальные по сложности алгоритмы относят к классу P-сложных. Среди экспоненциальных выделяют алгоритмы, основанные на переборе, и их относят в класс NP-сложных. Т.е. формально возможно существование экспоненциальных алгоритмов, основанных не на переборе. Например, n!, растущий быстрее, чем 2n. К NP-сложным относятся, например, задачи линейного целочисленного программирования, составление расписания, поиск кратчайшего пути в лабиринте и т.д. Обратим внимание, что все это так называемые дискретные задачи — на основе "неделимых" объектов.

В данном контексте мы и будем понимать термин "задача высокой сложности", представляя важность применения методов распараллеливания.

Управление обменом в сети типа "шина"

В этой топологии (рис. 3.4) возможно такое же централизованное управление, как и в "звезде" (т.е. физически сеть — "шина", но логически — "звезда"). При этом один из абонентов ("центральный") посылает всем остальным ("периферийным") запросы, выясняя, кто хочет передать, и затем разрешает передать одному из них. После окончания передачи абонент сообщает "центру", что он закончил, и "центр" снова начинает опрос. Все преимущества и недостатки такого управления - те же, что и в случае "звезды". Единственное отличие в том, что центр не перекачивает информацию от одного абонента другому, а только управляет доступом.

Рис. 3.4.  Сеть с общей шиной — логическая "звезда"
Однако чаще в "шине" реализуется децентрализованное управление, так как аппаратные средства абонентов одинаковые. При этом все абоненты также имеют равный доступ к сети, и решение, когда можно передавать, принимается каждым абонентом на месте, исходя из анализа состояния сети. Возникает конкуренция между абонентами за захват сети, и, следовательно, возможны конфликты между ними и искажения передаваемых данных из-за наложения пакетов.
Существует множество алгоритмов (сценариев) доступа, часто очень сложных. Их выбор зависит от скорости передачи в сети, от длины шины, загруженности сети (интенсивности обмена или трафика сети). Иногда для управления доступом к шине используется дополнительная линия связи. Это упрощает аппаратуру контроллеров и методы доступа, но заметно увеличивает стоимость сети в целом за счет удвоения длины кабеля и количества приемопередатчиков. Поэтому данное решение не получило широкого распространения.
Можно отметить ряд существующих методов обмена в сетях шинной архитектуры.

Простейший метод, используемый при выбранном коде обмена NRZ в сравнительно медленных сетях, — децентрализованный кодовый приоритетный арбитраж. Данный метод арбитража был предложен Институтом Проблем Управления (ИПУ) еще в начале 1970-х годов.
Он характеризуется низкой скоростью передачи, но высокой надежностью. Все абоненты имеют собственные приоритеты, которые могут динамически изменяться в зависимости от важности информации. При малой интенсивности обмена все абоненты равноправны (вероятность столкновений очень мала). Величина времени доступа к сети здесь не может быть гарантирована, так как абоненты с высокими приоритетами могут надолго занять сеть, не позволяя начать передачу абонентам с низкими приоритетами.

Второй метод, используемый в шине, — децентрализованный временной приоритетный арбитраж или метод доступа (рис. 3.5). Этот метод управления обменом обеспечивает более высокую скорость обмена, чем предыдущий (поскольку здесь нет ограничения на длительность каждого бита). Практически реализовать его так же сложно, как и предыдущий (каждый абонент должен отсчитывать свой временной интервал). Недостаток метода состоит также в том, что в случае большой длины сети и большого количества абонентов задержки становятся очень большими. Пример: при длине сети 1км, задержке сигнала в кабеле 4 нс/м и количестве абонентов 256 двойное время прохождения сигнала в сети 2L/V (L — полная длина сети, V — скорость распространения сигнала в используемом кабеле), или минимальная задержка составит 8 мкс. Следовательно, для абонента с сетевым адресом 255 задержка будет уже равна 255*8мкс=2040 мкс, т.е. около 2 мс, что уже довольно существенно. Для сравнения: если пакет имеет размер 1 Кбайт, то при скорости передачи 10 Мбит/с его длительность будет всего 0,8 мс. Данный метод не имеет жесткой привязки к коду передачи информации (в предыдущем методе можно было использовать NRZ). Код может быть практически любым, главное — выбрать его таким, чтобы можно было определять занятость сети.


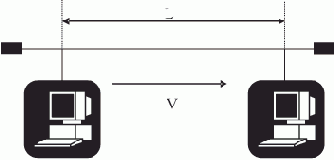
Рис. 3.5.  Обмен методом доступа

Третий метод, получивший довольно широкое распространение, можно считать развитием второго. Называется он CSMA/CD (Carrier-Sense Multiple Access/Collision Detection) или по-русски МДКН/ОК — метод доступа с контролем несущей и обнаружением коллизий (столкновений).


Идея метода состоит в том, чтобы уравнять в правах всех абонентов в любой возможной ситуации, то есть добиться, чтобы не было больших и малых фиксированных приоритетов (как в случае второго метода). Для этого используются времена задержки, вычисляемые каждым абонентом по определенному алгоритму.

К достоинствам метода CSMA/CD можно отнести полное равноправие всех абонентов, то есть ни один из них не может надолго захватить сеть. Метод достаточно надежен: ведь в течение всего времени передачи пакета идет контроль столкновений. К недостаткам метода относится то, что он не исключает повторения столкновений, а также плохо держит высокую нагрузку в сети. Обычно считается, что он хорош только до тех пор, пока нагрузка не превышает 30 \%, то есть только 30 \% времени сеть занята, а 70\% времени — свободна. Для сети Ethernet в среднем считается предельно допустимым 50\ldots100 абонентов, иначе возможны существенные нарушения обмена. Основной недостаток метода — негарантированное время доступа: нельзя сказать наверняка, через сколько времени пакет точно дойдет до приемника. В этом отношении он хуже, чем методы централизованного управления (методы опроса).

Звездообразная сеть IBM Token Ring, ARCnet)

"Звезда" — принципиально централизованная топология (рис. 3.1), в которой всегда есть четко выделенный центральный абонент, осуществляющий все управление обменом в сети, и через который идет вся информация в сети. В этом есть свои плюсы и минусы. Любое жестко централизованное управление по своей сути бесконфликтно, но такая сеть не будет работать при любой неисправности центрального абонента. Поэтому центральный компьютер должен отличаться от остальных высокой надежностью, а, следовательно, и более высокой стоимостью. К тому же, выполнять другие задачи на центральном компьютере станет невозможно, так как он будет загружен работой с сетью. К недостаткам топологии относится также ограниченное число абонентов, которое обычно в локальных сетях не превышает 16 пользователей. Затруднительно соединение звезд между собой. К плюсам данной конфигурации можно отнести ее малую чувствительность к выходу из строя соединительного кабеля. Разрыв кабеля в любом месте всегда нарушает связь только с одним абонентом.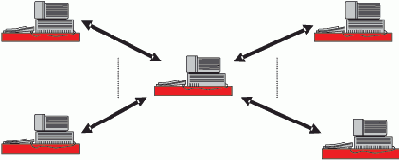

Рис. 3.1.  Сеть типа "звезда"

Параллельное программирование

Графический метод решения и его обобщение

Рассмотрим пример
z=c1x1+c2x2=2x1+5x2 max    (4.1)
при ограничениях
q1=x1 40
q2=x2 30
q3=x1+x2 50
и условиях x1 0, x2 0.
Каждое ограничение в двухмерном пространстве, n=2, определяет полуплоскость. Их пересечение образует многоугольник R (рис. 4.1). Его грани — прямые, получены на основе ограничений, в которых неравенства заменены равенствами.
q1 = 40
q2 = 30 (4.2)
q3 = 50
Эти равенства образуют уравнения границ или просто границы R.

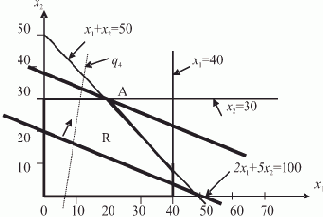
Рис. 4.1.  Графический метод решения задачи линейного программирования
Этот многоугольник (выпуклый многогранник; выпуклый, — ибо он остается по одну сторону от любой прямой, проходящей через его ребро) представляет собой допустимое множество решений R задачи ЛП.
Выберем произвольное значение, например, z=100 целевой функции. Прямая 2x1+5x2=100 показана на рисунке. Она пересекает ось x1 в точке x1=50 и ось x2 в точке x2=20.
Отметим, что для .
Т.к. dx1 и dx2 принадлежат прямой z, то скалярное произведение двух векторов, которое здесь изображено, равно нулю в том случае, если вектор (c1, c2) =(2, 5) перпендикулярен прямой z.
Увеличиваем значение z, передвигая (с помощью линейки) прямую — целевую — функцию параллельно самой себе в сторону ее возрастания вдоль вектора (2, 5) до тех пор, пока линейка не коснется последней возможной точки многогранника. R. Это значение z и будет максимальным. В данном случае — это точка A = (x1=20, x2=30).
Сделаем важное замечание относительно многогранника R.

То, что он выпуклый, мы заметили ранее.

Нам были заданы три ограничения, отсекающие полуплоскости, но определившие не все границы многогранника R. С "не закрытой" ими стороны область R оказалась закрытой условиями неотрицательного решения задачи: x1 0, x2 0. Значит, эти выражения пришлось из ранга условий перевести в ранг ограничений.
При этом не все условия могут быть переведены в ограничения. В нашей задаче могло существовать некоторое ограничение q4 (на рисунке пунктиром), которое бы определяло границу R слева, исключая границу x1 = 0.
При этом граница x2 = 0 внизу осталась бы.

Другое важное замечание: решение задачи мы нашли на границе многогранника R.

При этом возможны варианты:

Единственному конечному решению соответствует вершина R, как в нашем примере.

Решением может являться бесконечное множество точек на грани R, например, если бы ограничение q3 определяло бы прямую, параллельную z (уравнения q3 и z были бы линейно зависимыми).

Система ограничений может определять "открытый" многогранник R, включающий бесконечно удаленные точки, в которых достигается max z, т.е. max z = ?. Например, та же задача ЛП могла быть поставлена при отсутствии ограничений q2 и q3 (

рис. 4.2). Перемещение z в сторону ее увеличения может быть бесконечным, т.е. max z = ?. Но если бы была поставлена задача z min, то она бы при этих ограничениях имела конечное и единственное решение, в данном случае x1=x2=0.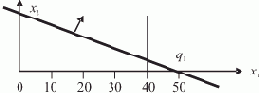

Рис. 4.2.  Случай отсутствия решения

Значит, имеет значение, с какой стороны многогранник R открыт: либо он позволяет поиск решения вдоль "закрытых" стенок, либо допускает возможность "выпасть" за его пределы, искать решение в бесконечности.

Тогда, как бы мы могли искать решение нашей первоначально поставленной задачи ЛП?

Учитывая, что решение задачи — в одной из вершин R, мы сначала выпишем уравнения всех прямых, ограничивающих R, т.е. уравнения всех его границ:

x1 = 40

x2 = 30

x1 + x2 = 50

x1 = 0

x2 = 0

Для нахождения координат каждой вершины R решаем совместно пару уравнений прямых, образующих эту вершину, и находим значение z в найденной вершине:



Действительно, max z = 190 достигается в точке A.

Отметим возможноcть распараллеливания решения задачи на многопроцессорной ВС, точнее, ВС SPMD-технологии.

В трехмерном пространстве ограничения и условия образуют пространственный многогранник R, охваченный плоскостями-границами, записанными на основе ограничений и условий, где неравенства заменены равенствами, а каждая плоскость z = const, среди которых мы ищем решение, пересекает, "прорезает" его, деля на две части (


рис. 4.3).


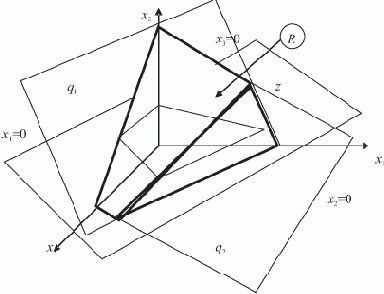
Рис. 4.3.  Задача линейного программирования в трёхмерной области

На рисунке иллюстрируется задача ЛП:

z=c1x1+c2x2+c3x3 max

при ограничениях

q1=a11x1+a12x2+a13x3 b1

q2=a21x1+a22x2+a23x3 b2

и при условии

x1 0, x2 0, x3 0.

Две грани q1=b1 и q2=b2, ограничивают многогранник R — область возможных значений переменных сверху (спереди) и справа. Слева, внизу и сзади пространственный многогранник R ограничен условиями неотрицательности решения, ставшими ограничениями x1 = 0, x2 = 0, x3 = 0. Плоскость z=const пересекает многогранник R. Перемещая плоскость z параллельно себе, т.е. вдоль вектора (c1, c2, c3), в сторону возрастания значений линейной формы z, мы находим решение. Здесь наглядно показана очевидность того, что решение следует искать в вершинах R.

Однако графическое представление уже в трехмерном пространстве затруднительно, в n-мерном пространстве нам необходимо действовать формально. Здесь существует ряд проблем.

Во-первых, мы не представляем пространственной картины и не знаем, охватывают ли заданные ограничения область R со всех сторон и какими условиями эти ограничения должны быть дополнены без противоречий.

Во-вторых, мы не знаем, какие n ограничений, дополненных условиями, соответствуют каждой конкретной вершине многогранника R, чтобы найти координаты этой вершины и найти в ней значение целевой функции z. Значит, мы должны испытать все возможные комбинации по n (в данном случае — тройки) ограничений и условий, т.е. все возможные комбинации по три, составленные на основе всех потенциальных границ- ограничений и условий.

Тогда при построении (параллельной!) вычислительной процедуры мы должны опираться на то, что любая противоречивость в системе ограничений (в их состав мы включили теперь и условия) выразится в неразрешимости системы трех уравнений, составленной для нахождения координат очередной испытываемой вершины R. Т.е. в этом случае вершина находится в бесконечности или содержит отрицательные значения координат. Эта неразрешимость находится в процессе счета.


Оставаясь в области практических решений задач ЛП, т.е. в области инженерии и экономики, примем предположение, что задача сформулирована корректно. Под этим будем предполагать, что ограничения выбраны так, что она не имеет неограниченного решения z = ?.

Например, ставя задачу о максимизации прибыли от перевозки, не надо забывать о том, что объем перевозок ограничен ресурсами страны, сообщества и т.д. В противном случае мы получим тривиальное решение: чем больше, тем лучше.

Значит, мы будем предполагать, что в многограннике R обязательно есть вершины (их координаты не отрицательны), в целом ограничивающие области изменения переменных, и хотя бы в одной из этих вершин целевая функция — линейная форма z принимает максимальное значение.

В свете сказанного будем также считать, что ограничения не противоречивы. Противоречивые ограничения приводят к случаю R = .

Например, ограничения

x + y 5

x + y 2

противоречивы.

Тогда, развивая на n-мерное пространство, мы можем реализовать следующую стратегию поиска решения задачи ЛП.

Общий алгоритм перебора

На основе ограничений задачи q1 b1, ... qm bm строим систему граней (гиперплоскостей) q1 = b1, ... qm = bm. Дополним эту систему граней всеми потенциальными гранями на основе условий: x1
= 0, ... , xn = 0. Получим систему m+n линейных уравнений, в общем случае избыточную и, возможно, противоречивую.

Выбираем из этой системы очередную подсистему n линейных уравнений (всего таких подсистем Cnm + n) и решаем ее.
Как известно, система n линейных уравнений имеет единственное решение в том и только в том случае, если ранг r матрицы системы равен рангу расширенной матрицы системы и равен n.
Можно в вычислительную процедуру включить анализ соответствующих матриц. Можно ограничиться анализом только определителя системы, его отличием от нуля, т.к. нас интересует лишь единственное решение. Однако ориентация на современные вычислительные средства и их операционные системы позволяет этого не делать.
Дело в том, что любой метод решения системы линейных уравнений в случае неразрешимости системы или неоднозначности решения столкнется с операцией деления на нуль — т.е. возникнет прерывание. Этим целесообразно активно пользоваться для упрощения вычислительной процедуры.
После обработки прерывания необходимо предусмотреть переход к решению следующей, очередной подсистемы линейных уравнений, если такие еще не исчерпаны.
Однако традиционно при решении систем линейных уравнений в подобных задачах используют метод Гаусса как обобщение метода последовательного исключения. Метод Гаусса позволяет получать значения переменных последовательно. Значит, их контроль на отрицательность производится немедленно и останавливает дальнейший счет. Кроме того, попутные преобразования системы уравнений позволяют динамически выявить тот случай, когда матрица — алгебраическое дополнение диагонального элемента содержит нулевую строку, т.е. определитель системы равен нулю. Это также останавливает дальнейший анализ системы уравнений.
Если же получено единственное решение и все его компоненты x1, ... , xn не отрицательны, то они могут определять вершину многогранника R.
Могут, ибо если среди уравнений подсистемы есть уравнения вида xj = 0, введенные в состав граней на основе условий неотрицательности решений, и не вошли все уравнения граней, обусловленные ограничениями задачи, то полученное решение может противоречить некоторым "законным" ограничениям задачи. А именно — не представленным в составе решенной подсистемы.

Поэтому в таком случае необходимо дополнительно проверить, принадлежит ли действительно точка (x1, ... , xn) многограннику R, т.е. выполняются ли для нее все не отображенные в подсистеме ограничения вида qj bj, первоначально указанные при постановке задачи ЛП.

Если найденная точка (x1, ... , xn) действительно является вершиной многогранника R, определяемого ограничениями и условиями при постановке задачи, отыскивается значение z(x1, ... , xn) = c1x1+c2x2+ ... +cnxn. Если это значение превосходит ранее полученные при уже проведенном анализе других вершин, оно запоминается вместе со значениями x1, ... , xn — для продолжения поиска и анализа других вершин R или окончания решения задачи.

Перебор всех подсистем n линейных уравнений на основе m+n ограничений (исходных и дополнительных), их число Cnm+n, полученные при их решении координаты вершин многогранника R, обусловленного числом m основных ограничений, позволяет выбрать ту вершину, которая порождает максимальное (минимальное) значение целевой функции — линейной формы z.

Данная вычислительная процедура хорошо реализуется на многопроцессорных ВС. Различные варианты подсистем линейных уравнений следует динамически распределять между процессорами. А это, в свою очередь, полностью соответствует SPMD-технологии "одна программа — много потоков данных".

О единственности решения. Мы видели по рисункам, что z = zmax может выполняться на ребрах и гранях многогранника R. Если на ребре, то в двух сопряженных вершинах z принимает одинаковое значение zmax. Если на гранях, то более чем в двух вершинах z = zmax . Это легко переносится в n-мерное пространство.

Итак, указанная вычислительная процедура может привести к получению единственной вершины X = (x1, ... , xn) многогранника R, в которой z(X) = zmax.

Пусть в r вершинах X1, ... , Xr многогранника R выполняются равенства z(Xj) = zmax, j = 1, ... ,r. Построим выпуклую комбинацию векторов:

X = k1 X1 + k2 X2 + ... + kr Xr , k1 + k2 + ... + kr = 1, kj 0. (4.3)

Множество значений X, удовлетворяющих этому условию, определяет бесконечное множество решений данной задачи ЛП.

Легко видеть, что данная вычислительная процедура предполагает любое соотношение n m.

Общий алгоритм

Формируем систему m + n уравнений

(4.13)

действительных и возможных границ многогранника R допустимых решений. Эта система уравнений отображает m заданных ограничений и n условий неотрицательности решения.

Решая совместно подмножество n уравнений этой системы, находим одну из вершин X0 многогранника R. Находим значение z0
целевой функции в точке X0.

Дополним систему n уравнений, первоначально породившую вершину X0, теми уравнениями, которым X0 также удовлетворяет. Получим систему p n уравнений, порождающих вершину X0.

(4.14)

Примечание 1. Теперь наша задача — переместиться вдоль одного из ребер, исходящих из вершины X0, в смежную вершину X1, такую, что Z(X1) > Z(X0). При этом, желая ускорить процесс (хотя выбор стратегии нуждается в обосновании), будем среди всех смежных вершин искать ту вершину X1, в которой достигается максимальное увеличение значения целевой функции. Каждое ребро описывается системой n - 1 уравнений из состава p уравнений, породивших испытываемую вершину X0. Введем переменную p, первоначально приняв p = n

Выбирая из (4.14) по n - 1 уравнений, будем получать систему, которая определяет некоторое ребро, исходящее из X0. Всего таких подсистем может быть Cpn - 1.

Последовательно испытываем данное ребро на его пересечение с теми из m гранями из (4.13), которые не вошли в состав (4.14). Т.е. дополняем нашу систему n - 1 уравнений очередной испытываемой гранью. Получаем систему n уравнений и решаем ее. Возможны следующие варианты.

Система не имеет решения, имеет не единственное решение или решение содержит отрицательные компоненты. Переходим к испытанию следующей грани.

Система имеет неотрицательное решение, но это решение не удовлетворяет всем m ограничениям задачи, т.е. находится вне R. Переходим к испытанию следующей грани.

Система имеет неотрицательное решение X1 X0, удовлетворяющее всем m ограничениям задачи. Значит, найдена смежная вершина. Если Z(X1) < Z(X0), переходим к испытанию следующего ребра — к выполнению шага 6.
Если Z(X1) = Z(X0), запоминаем вершину X1. Это для случая, если в результате проводимых испытаний оказалось, что точка X0 — решение задачи. Тогда необходимо знать все вершины, образующие решение, чтобы построить общее параметрическое выражение. Переходим к испытанию следующего ребра. Если Z(X1) > Z(X0), запоминаем точку X1 в данном качестве и переходим к испытанию следующего ребра.

Примечание 2. Возможна стратегия, при которой смещение производится в первую же найденную вершину с превышающим значением целевой функции. Есть вариант, что это — более правильная стратегия, т.к. значительное увеличение значения целевой функции на данном шаге может привести в дальнейшем к увеличению числа шагов: мы ничего не знаем о особенностях многогранника решений. Мы же здесь рассматриваем стратегию, при которой отыскивается смежная вершина с максимальным превышением целевой функции.

Перебрав все грани для одной подсистемы n - 1 линейных уравнений (для одного ребра), формируем другую подсистему таких уравнений на основе (4.14). Анализируем ее совместно со всеми m + n - p уравнениями из (4.13).

Таким образом, исследовав все ребра, исходящие из X0, мы можем найти ту смежную вершину X1, где целевая функция максимально превышает ее значение в исходной вершине. Перемещаемся в эту вершину, полагая X0 = X1. Система (4.14) теперь — та система n уравнений, решение которой породило X1. Дополняем ее уравнениями других граней, проходящих через X1. Получаем p n. Начинаем весь процесс перемещения сначала. Однако первое ребро, определяемое первыми n - 1 уравнениями (4.14), это ребро, которое ведет в вершину, из которой мы вышли. Т.е. первую комбинацию n - 1 граней следует пропустить.

Если не удается найти вершину, в которой значение целевой функции превышает ранее найденное, то мы нашли решение. Одновременно мы нашли и сохранили те смежные (проанализированной вершине!) вершины, в которых значения целевой функции равны. Однако мы могли найти не все вершины, обладающие одним, максимальным, значением Z.


Ведь мы двигались только по ребрам, исходящим из предыдущей анализируемой вершины. "Напротив" этой вершины могут быть другие вершины с тем же значением целевой функции, и в эти вершины не ведут ребра из данной. Однако на основе свойств выпуклого многогранника можно заключить, что отношение взаимной смежности связывает все вершины, образующие решение задачи ЛП. Т.е. вершины-решения, не смежные друг другу, являются смежными другим вершинам-решениям. Существует путь вдоль ребер, связывающий вершины-решения. Тогда можно построить алгоритм выявления всех вершин R — решений задачи ЛП.

Пусть найденные уже вершины-решения образуют множество A. Дополним его последней найденной вершиной. Выбираем первую из ранее запомнившихся вершин из A с равным, максимальным, значением целевой функции и делаем ее опорной, X0.

Выполняем шаги 4-8 для поиска вершины многогранника R с более высоким значением Z, чем значение Z(X0). Конечно, мы такой вершины найти не можем. Но мы можем найти новую вершину X, не входящую в множество A, такую, что Z(X) = Z(X0). Включаем вершину X в A, полагаем X0 := X. Продолжаем выполнение данного пункта до тех пор, пока множество A не перестанет пополняться новыми вершинами. Производим параметрическую запись (4.4) общего решения задачи.

Параллельное решение задачи целочисленного линейного программирования

Методы параллельного решения задачи ЛП, основанные на непосредственном перемещении по ребрам многогранника решений, не привлекая дополнительных переменных, способствуют построению наглядного метода решения соответствующей задачи линейного программирования (задачи ЦЛП). Под соответствием мы понимаем добавление условия целочисленности решения при той же формальной постановке задачи ЛП.
Такой метод основан на захвате в "вилку" некоторой целой точки внутри многогранника решений, вблизи точки решения задачи ЛП.
Рассмотрим пример.
Решим задачу ЦЛП:
Z = x - 3y + 3z max
при ограничениях
2x + y - z 4
4x - 3y 2
-3x + 2y + z 6
и при условиях x, y, z 0, целые.
Решение задачи ЛП достигается (рис. 4.5) в точке (0,5, 0, 7,5), которая является результатом решения системы уравнений — граней
q2 = 4x - 3y - 2 = 0
q3 = -3x + 2y + z - 6 = 0
q5 = y = 0
Значение целевой функции Z(0,5, 0, 7,5) = 23.

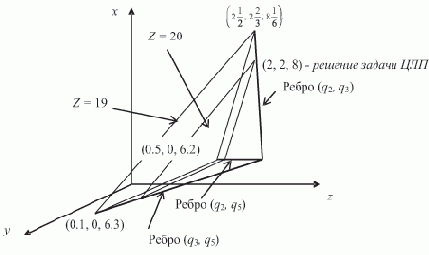
Рис. 4.5.  Решение задачи целочисленного линейного программирования
Положим ? Z = 4, и найдем все точки пересечения образовавшейся "целевой плоскости" с ребрами, исходящими из вершины-решения. Для ребра (q2, q3)
Все координаты при переходе из вершины-решения в найденную точку превысили некоторые целые значения. Причем, одна из координат "преодолела" именно ближайшее целое, заставив другие координаты "преодолеть" большее число единиц.
Для ребра (q2, q5)
Не все координаты "преодолели" ближайшее целое значение: x остался внутри интервала (0, 1).
Для ребра (q3, q5)
Опять не все координаты "преодолели" ближайшее целое: x остался внутри интервала (0, 1).
Значит, только в точке
наблюдается "преодоление" целых значений по сравнению с точкой (0,5, 0, 7,5), представляющей точное решение задачи ЛП. Т.е. нам удалось захватить решение задачи ЦЛП в "вилку". При этом точка (2, 2, 8), "преодоление" которой произошло, — возможное решение задачи ЦЛП.
Однако для того, чтобы координате z преодолеть ближайшее целое значение, координатам x и y пришлось преодолеть по два целых значения. Поэтому закономерен вопрос о том, нет ли внутри отсеченной с помощью ? Z области целых точек, где z преодолевает ближайшее целое с меньшей ценой для других координат. Ведь значение целевой функции в таких точках было бы больше.
Половиним "вилку". Положим ? Z = 2 и найдем точки пересечения "целевой плоскости" Z = 21 c ребрами, исходящими из вершины-решения задачи ЛП:
Видим, что есть координата, , которая не "преодолела" ближайшее целое, определяемое решением задачи ЛП. Там z =7,5. Очевидно, что на других двух ребрах ситуация тем более останется прежней.
Вновь половиним "вилку" в сторону увеличения значения ? Z, пытаясь вплотную подойти к возможной целой точке, где значение Z максимально. Положим ? Z = 3. Найдем точки пересечения "целевой плоскости" Z = 20 с ребрами, исходящими из вершины-решения задачи ЛП.
Решаем первую систему.
Решение "преодолело" целые значения по всем координатам. Не менее чем по одной координате произошло округление до ближайшего целого. Более того, по всем координатам получены целые значения. Дальнейший поиск прекращается, решение задачи ЦЛП найдено.
Если бы решение не совпало с целым, мы проверили бы точки пересечения "целевой плоскости" с другими ребрами. Вместе с тем, это можно и не делать, т.к. для меньшего значения Z = 19 уже установлен факт "непреодоления" там целых значений. Так что нам осталось бы только выполнить округление.
Рассмотренные в лекции методы решения задач линейного программирования имеют важную методологическую направленность, обусловленную наглядностью, ощутимостью, чувством "физического смысла" задач. Их роль не осмысленна до конца, но они позволяют эффективно распараллеливать вычисления. В этом смысле такие методы, как симплекс-метод, венгерский метод ориентированы исключительно на последовательные вычисления, но зато полностью исключают перебор. Для большой размерности задачи введение дополнительных переменных, что предполагается в симплекс-методе, может показаться нежелательным.
Предложен вполне практический метод (хотя и не описан алгоритмически) решения задачи ЦЛП, опирающийся на нахождение хотя бы одного решения соответствующей задачи ЛП. Мы не затронули вопроса о единственности решения — как задачи ЛП, так и задачи ЦЛП, о произвольном числе ребер, образующих вершину-решение задачи ЛП. Метод, несомненно, подлежит развитию. Его достоинство заключается в том, что он, по сравнению с методом "ветвей и границ", не требует многократного решения задачи ЛП с динамически уточняющимися и размножающимися ограничениями.
Можно указать на осуществляемое практическое применение предлагаемых методов в качестве тестовых задач для оценки эффективности многопроцессорных ВС, использующих принципы SPMD-технологии ("единственная программа — много потоков данных"). Эти же методы используются при разработке сетевых технологий решения сложных задач.

План параллельных вычислений

Воспользуемся в основном той же схемой вычислений, что и в разделе 4.1.
Пусть все процессоры ВС или используемые станции локальной сети обладают своим номером и знают количество используемых средств. Как показывалось ранее, они все начинают решать "свои" системы линейных уравнений. Здесь уже можно применить различные стратегии. Одна из них: пусть хотя бы один процессор нашел вершину многогранника R. Ее можно взять за вершину X0.
Другая стратегия заключается в том, чтобы дать возможность всем участвующим процессорам найти по одной вершине R. Вершину с максимальным значением целевой функции Z можно взять за X0.
Выбрав вершину X0, все процессоры начинают решать "свои" варианты систем линейных уравнений в поисках смежных вершин с превышающим значением целевой функции. Согласовав действия при нахождении вершины X1 и приняв X0 := X1, они продолжают процесс движения по ребрам R.

Предпосылки методов

Задачи линейной и нелинейной оптимизации, сетевые транспортные задачи — задачи высокой сложности, подверженные "проклятию размерности". Ориентация на применение многопроцессорных симметричных вычислительных систем в составе персональных компьютеров или рабочих станций (параллельные вычисления) и на применение сетевых технологий (распределенные вычисления) требует разработки новых параллельных методов их решения. Эти методы должны быть лишены недостатков "традиционных" методов: последовательного характера вычислений и введения дополнительных переменных (для задач линейного программирования). Анализ способов распараллеливания показывает эффективность распараллеливания "по информации". Весьма перспективной поэтому становится SPMD-технология программирования (Single Program — Multiple Data). При этой технологии вычислительный процесс строится на основе единственной программы, запускаемой на всех процессорах вычислительной системы или на многих станциях локальной сети. Копии программы могут выполняться по разным ветвям алгоритма, обрабатывая подмножества данных. Неизбежна синхронизация во времени и при обработке общих данных.
Такая технология параллельного программирования и обусловила разработку рассмотренных ниже методов. В то же время не отрицаются известные традиционные методы, сокращающие общее число операций и исключающие перебор. Иной методологический подход открывает дорогу решению задач большой размерности и эффективной параллельной работе многих процессоров. Для ряда задач этот подход еще нуждается в исследовании, уточнении области применения и развитии — проведении тщательной математической экспертизы. Поэтому мы посчитали необходимым осветить его подробно — для лучшего представления "физического смысла", ощутимости пространственной модели задач и следующих из этого планов их параллельного решения.

Пример применения параллельной процедуры прямого перебора

Решим ту же задачу (2), подойдя формально, по правилу, пригодному для любой размерности пространства.
Исходная система уравнений действительных или потенциальных плоскостей — граней R имеет вид

(4.4)

Т.к. C23+2=10, исследование десяти комбинаций (подсистем уравнений) по два уравнения из (9.4) выглядит следующим образом.

Подставляем это уже готовое решение в третье ограничение задачи, x1+ x2 50, и отвергаем его, т.к. ограничение не выполняется.

Решение удовлетворяет третьему ограничению x2 30.
Находим и запоминаем z(40, 10) = 130.

Система не имеет решения.

Решение удовлетворяет ограничениям
Находим z(40, 0) = 80. Если мы решаем задачу не на параллельном компьютере, то сразу же видим, что новое значение z не превосходит уже найденное. Поэтому и это решение отвергаем.

Решение x1 = 20, x2 = 30 удовлетворяет и третьему "основному" ограничению задачи x1 40. Находим z(20, 30) = 190. Запоминаем его вместе с решением, т.к. оно превосходит ранее полученное.

Решение удовлетворяет всем ограничениям задачи. z(0, 30) = 150, что не превосходит уже найденное значение. Решение отвергаем.

Не имеет решения.

Решение x1 = 0, x2 = 50 противоречит "основному" ограничению x2 30. Отвергаем его.

Решение x1 = 50, x2 = 0 противоречит "основному" ограничению x1 40. Отвергаем его.

Решение не противоречит "основным" ограничениям задачи. Однако z(0, 0) = 0, что не превосходит уже найденное значение. (Кстати, оно обеспечивает решение задачи z min.)

Итак, x1 = 20, x2 =30 обеспечивает zmax =190, т.е. является решением задачи ЛП.

допустимых решений, представленный на рис.

Рассмотрим задачу линейного программирования
Z = 26x + 20y + 21z max (4.6)
при ограничениях
q1 = 2x + 7y - 76z + 222 0
q2 = - 8x +9y - 8z + 64 0
q3 = - 8x + 13y -24z + 96 0 (4.7)
q4 = - x - 6y - z + 70 0
q5 = - 2x - 7y - 2z + 90 0
q6 = 33x + 3y +22z - 165 0
и при условии x 0, y 0, z
0.
Ограничения и условия образуют многогранник R(ABCDEFGHKL) допустимых решений, представленный на рис. 4.4.

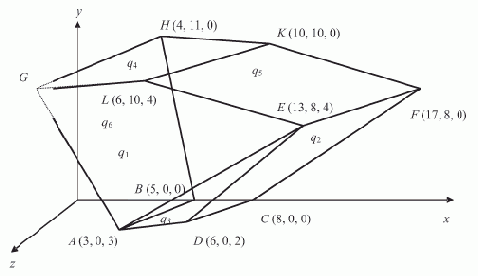
Рис. 4.4.  Многогранник допустимых решений
Формально мы не знаем R, и множество граней — действительных и возможных — этого многогранника представлено системой уравнений:
q1 = 2x + 7y - 76z + 222 = 0
q2 = - 8x +9y - 8z + 64 = 0
q3 = - 8x + 13y -24z + 96 = 0
q4 = - x - 6y - z + 70 = 0
q5 = - 2x - 7y - 2z + 90 = 0 (4.8)
q6 = 33x + 3y +22z - 165 = 0
q7 = x = 0
q8 = y = 0
q9 = z = 0
В результате решения первой же подсистемы трех уравнений (n = 3) системы (4.8) получаем координаты вершины E многогранника R

(4.9)

Постараемся "сместиться" в ту вершину, смежную вершине E, т.е. соединенную с ней ребром (в одну из вершин A, D, L, F), в которой целевая функция Z имеет максимальное значение, превышающее Z(E).
Ребра, исходящие из вершины, определяются подсистемами n-1 плоскостей, пересекающихся в этой вершине, т.е. образующими ее.
В данном случае подсистема определяет несуществующее ребро. Пока мы знаем это только по рисунку. Подсистема
определяет ребро EA, подсистема

определяет ребро ED. А вот ребра EL и EF мы пока не знаем, т.к. не знаем (формально, а не по рисунку!) все плоскости (плоскость q5), пересекающиеся в E. Это значит, что из каждой вершины в общем случае исходят не менее n ребер, а сколько в действительности — предстоит уточнить. (Представьте себе R — бриллиант классической огранки.)
Значит, q1, q2, q3 — это лишь наше начальное представление о множестве плоскостей — граней, пересекающихся в вершине E. Нам необходимо развить это представление до полного.
Тогда выясним все множество граней, образующих вершину E, подстановкой ее координат во все другие уравнения (9.8) и испытанием на получение тождества.
Находим q5(13, 8, 4) 0. Добавляем q5 в (4.9), полагаем полностью известным число p = 4 ребер, образующих вершину E. Т.е. вместо (4.9) получаем

(4.10)

Каждую возможную грань, определяемую двумя (n-1) уравнениями плоскостей из (4.10), будем решать совместно со всеми плоскостями из (4.8), не вошедшими в (4.10), — с гранями q4, q6, q7, q8, q9.
Первая такая система имеет вид

(4.11)

Ее решение (535, 8,7, -517,2) содержит отрицательную составляющую. Т.е. эта точка не принадлежит R. Если бы решение было не отрицательным, мы должны были бы проверить выполнение всех ограничений (4.7), не представленных в (4.11).
Можно показать, что в выпуклом многограннике несуществующее ребро не вызовет появления "ложной" вершины, и достаточно проверить (4.7).
Системы
имеют не положительное решение.
Следующая испытываемая система линейных уравнений на основе двух уравнений из (4.10) и не входящих в (4.10) уравнений из (4.8), имеет вид
Ее решение — приблизительно точка (5,2, 9,4, 4) не является вершиной R, т.к. не удовлетворяет всем ограничениям (9.7), q5(5,2, 9,4, 4) < 0.
Следующая испытываемая система имеет вид
Ее решением является вершина A (3, 0, 3), Z(A) = 141 < 592.
Т.к. мы нашли вершину на "другом конце" ребра, анализ данного ребра прекращаем.
Следующее исследуемое ребро, исходящее из вершины E, определяется подсистемой
которая должна решаться совместно с уравнениями q4 = 0, q6 = 0, q7
= 0, q8 = 0, q9 = 0.
Первая же система определяет вершину L (6, 10, 4). Однако Z(L) = 440 < 592.
Следующее возможное ребро, исходящее из вершины E, определяется комбинацией
Решая ее совместно с другими гранями R, - q4 = 0, q6 = 0, q7
= 0, q8 = 0, q9 = 0, пытаемся найти другую вершину в R, смежную E.
Очередная решаемая система уравнений
имеет не отрицательное решение (13,625, 8,7, 4,175). Проверяем выполнение ограничений (9.7), не представленных в решенной системе. Находим, что q1(13,625, 8,7, 4,195) < 0. Этой проверки достаточно для вывода о том, что найденная точка не является вершиной многогранника R.

Системы
и
имеют решение в отрицательной области.
Система
определяет вершину D (6, 0, 2), для которой Z(D) = 198 < 592.
Следующее возможное ребро по (4.10) определяется парой граней
Решаем совместно с остальными гранями, не входящими в (10): q4 = 0, q6 = 0, q7 = 0, q8 = 0, q9 = 0.
Система
не имеет решения, ранг матрицы системы не равен рангу расширенной матрицы.
Система
имеет отрицательное решение.
Система
имеет неотрицательное решение, при котором q1 < 0. Найденная точка не является вершиной R.
Система
не имеет решения.
Система
имеет неотрицательное решение — точку F (17, 8, 0), удовлетворяющую всем ограничениям: q1(17, 8, 0) > 0, q3 (17, 8, 0) > 0, q4(17, 8, 0) > 0, q6(17, 8, 0) > 0. Точка F — вершина многогранника R. Z(F) = 602 > 592.
Таким образом, мы нашли вершину F, смежную вершине E, с превышающим значением целевой функции. Однако поиск всех вершин на основе (4.10), смежных вершин E, следует продолжить. Ведь формально возможна и другая вершина, с еще большим значением целевой функции.
Перебор продолжаем на основе ребра
хотя мы видим по рисунку, что такого ребра нет.
Ищем точки пересечения этого ребра со всеми гранями R, не вошедшими в (4.10).
Система уравнений
имеет решение (0,875, 10, 9,125).
При проверке выполнения первого же ограничения оказывается, что q1(0,875, 10, 9,125) < 0. Найденная точка действительно не является вершиной R.
Система
имеет отрицательное решение.
Система
имеет решение (0, 10,144, 9,5), не удовлетворяющее первому же ограничению.
Система
имеет отрицательное решение.
Система
имеет не отрицательное решение (22,96, 6,44, 0), не удовлетворяющее ограничениям.
Таким образом, анализ всех возможных вершин, смежных вершине E, закончен. Мы нашли единственную вершину F(17, 8, 0), где значение целевой функции Z(17, 8, 0) = 602 превышает ее значение в точке E. Система уравнений, определившая эту вершину, имеет вид

(4.12)

Если бы мы нашли несколько вершин с одинаковым значением целевой функции, то были бы возможны различные стратегии дальнейших действий.


Мы здесь рассматриваем случай, когда для дальнейшего поиска фиксируется одна из таких вершин. Других граней, которым принадлежит точка F, нет. Смещаемся в эту вершину, полагаем p = 3.
Начинаем весь процесс поиска смежной вершины с максимальным (среди смежных вершин) значением целевой функции Z, обязательно превышающим значение Z(F).
Первое возможное ребро, исходящее из F, определяется уравнениями
Однако эта комбинация возвращает нас в ту вершину, которую мы уже исследовали. Поэтому сразу же переходим к следующему возможному ребру

решая его совместно с гранями q1, q3, q4, q6, q7, q8.
Система
решалась ранее. Ее решение неположительно. (Если мы переупорядочим уравнения системы по индексам, то получим индексный код, по которому будем входить в таблицу с информацией о решенной ранее системе. Так мы реализуем самообучение в процессе решения.)
Система
решалась ранее. Ее решение также содержит отрицательный компонент.
Система
решается впервые. Ее не отрицательное решение не удовлетворяет всем ограничениям, q3(17,8, 8,7, 0) < 0.
Системы
и
имеют решения, содержащие отрицательные компоненты.
Система
определяет вершину C, Z(8, 0, 0) = 208 < 602.
Следующее исследуемое ребро определяется системой уравнений
Система
исследовалась раньше. Она не имеет решения.
Система
решалась ранее. Она определяет точку, не являющуюся вершиной R.
Система
решается впервые. Она определяет точку K. Однако Z(10, 10, 0) = 460 < 602.
Таким образом, нам не удалось сместиться из вершины F в вершину с большим значением Z. Значит, найденная точка F определяет решение задачи ЛП.

Сложность алгоритма прямого перебора

Основным элементом решаемой задачи является решение системы n линейных уравнений. Сложность решения такой системы можно считать полиномиальной O(n3). Число решений определяется как Cnm+n. Чтобы найти зависимость сложности от основных параметров n и m, определим, во сколько раз увеличивается сложность при увеличении размерности n на единицу:

(4.5)

Если считать, что m соразмерно с n, т.е. m n, то увеличение размерности n на единицу при больших n примерно в два раза увеличивает сложность задачи, т.е. ее сложность определяется как O(2nn3). Это экспоненциальная сложность, практически сильно ограничивающая размерность решаемых задач.
Простота параллельного алгоритма прямого перебора делает его привлекательным для значений n порядка двух-трех десятков. Для большей размерности необходимо искать алгоритмы полиномиальной сложности.

Сложность алгоритма

Если считать, что чаще всего из одной вершины исходят n граней, то число решаемых систем n линейных уравнений при поиске смежных вершин определяется как
r = n ? (m + n - n) = n ? m.
Число вершин k, по которым производится перемещение в поисках решения, предсказать трудно. Однако очевидно, что k << Cnm + n, т.к. лишь локально затрагивается некоторый "бок" многогранника R. Считая, как и раньше, m n, можно оценить сложность решения данным методом, как O(kn5). Эта сложность является полиномиальной.

Параллельное программирование

Алгоритм

Пусть стек составляют нуль-единичные строки длины n (число каналов сети). Для каждой строки известно упорядоченное по номерам множество M каналов, логическая сумма строк которых в матрице S определила данную строку. Номер k последнего канала в этом множестве известно. Для каждой строки известен последний испытанный нулевой элемент.

Загружаем очередную i -ю, i = 1, ... ,n-1, строку в стек. Полагаем M ={i}, k = i.

В строке-вершине стека находим очередной нуль, занимающий позицию j > i. Переходим к выполнению шага 4.

Если такого нуля нет, или все они испытаны, строку исключаем из стека. Если после этого стек исчерпан, выполняем шаг 1. В противном случае выполняем шаг 2.

Складываем логически строку из вершины стека со строкой j — формируем новую вершину стека. Номером канала j дополняем множество каналов M, участвующих в формировании новой строки. Полагаем k = j.

Если в строке-вершине стека все нули соответствуют только всем каналам в M, то M — очередное найденное ПМВНК. Фиксируем это множество. В любом случае исключаем строку-вершину стека из стека. Выполняем шаг 2.

Исходные построения

Исследование потоков в сети — важная, всегда актуальная задача исследования операций. Она лежит в основе моделирования при проектировании как транспортных сетей, так и сетей водоснабжения и канализации. Известен ряд классических моделей (приводимых, например, в [15]) в этой области. Важнейшую роль играют модели, позволяющие определить "узкие" мести сети. Они определяют ее максимальную пропускную способность между выделенными пунктами, или, иначе говоря, ее минимальное сечение. Это задача дискретного программирования, широко использующая перебор и относящаяся к задачам высокой сложности.
При аналитическом моделировании сети используется известный [15] алгоритм Форда-Фалкерсона.
Теория параллельного программирования способна предложить более простой алгоритм перебора. Его достоинством является параллелизм, который позволяет эффективно использовать многопроцессорные ВС и вычислительные комплексы на основе рабочих станций локальной сети. Возможен наиболее простой способ распараллеливания на основе применения SPMD-технологии.
Пусть задана сеть (рис. 5.1). Дуги ее назовем каналами. Каналы пронумерованы. Направление потоков показано стрелками. Вершины — точки сопряжения каналов, вершина A — исток, вершина B — сток. Каждая дуга i сопровождается информацией об интересующих нас характеристиках потока, например, о пропускной способности di канала. В этом случае правомерен вопрос о максимальной пропускной способности сети, обусловленной минимальным сечением.

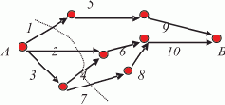
Рис. 5.1.  Сеть для оценки пропускной способности
В терминах теории параллельного программирования (лекция 7) каждое сечение сети (например, сечение, пересекающее каналы 1, 2, 4, 7) является полным множеством взаимно независимых работ — каналов (ПМВНК). Перебрав все такие множества и рассчитав для каждого суммарную пропускную способность, мы можем найти минимальное значение. Оно характеризует минимальное сечение, а следовательно, максимальный возможный поток в сети.
В [3] приводится алгоритм перебора всех полных множеств взаимно независимых работ.
Усовершенствуем его, получая такие множества, упорядоченные по номерам каналов, и исключая повторное нахождение одних и тех же полных множеств. (В лекции 7 изложенные ниже преобразования будут рассмотрены глубже.)

Построим треугольную матрицу следования S, отражающую граф сети (рис. 5.2а). Сложив каждую последующую строку с теми предыдущими, которые соответствуют единичным элементам этой строки, получим матрицу следования S с транзитивными связями (рис. 5.2б). Транспонируем матрицу S и объединим с ее начальным видом (рис. 5.2в). Иначе, отобразим S симметрично относительно главной диагонали. Получим матрицу S, отображающую как порядок следования, так и порядок предшествования каналов.


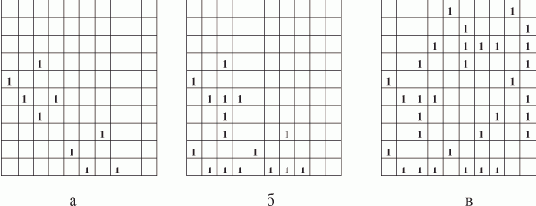
Рис. 5.2.  Полная матрица следования каналов:а — начальный вид, б — дополнение транзитивными связями, в — конечный вид

Теперь матрица S полностью отражает взаимную независимость каналов. Например, если сложить логически строки 1, 2, 3, то получим строку, содержащую нули только в позициях 1, 2, 3. Тем самым мы получим ПМВНК {1, 2, 3}. Множество полное, т.к. дополнительное сложение с любой другой строкой изменит состав нулей.

Таким образом, наша задача заключается в том, чтобы испытать все варианты сложения групп строк так, чтобы нули в строке-результате оказывались в тех и только в тех позициях, которые соответствуют строкам- слагаемым. Тогда эти строки определят очередное ПМВНК. Упорядочение по номерам строк поможет нам избежать повторного получения ПМВНК с другим порядком следования номеров каналов.

О применении схемы Гаусса решения систем линейных уравнений в транспортной задаче

Остался неясным вопрос: приходится ли в общем случае при решении систем линейных уравнений для данной задачи пользоваться схемой Гаусса, или достаточно последовательно пользоваться простыми подстановками?
Подстановки мы легко выполняли в том случае, если в результате введения нулевых комбинаций у нас получались уравнения, содержащие в левой части единственную переменную. Если таких уравнений нет, то очевидна целесообразность применения схемы Гаусса.
Тогда выясним, существует ли комбинация нулей, такая, при которой в каждой строке A, с учетом неисключенной строки, остается не менее двух единиц.
Рассмотрим только n = 4 последних уравнений из (5.6): три последних уравнения из (5.7) и уравнение y4 + y8 + y12 = 7. Их матрица имеет вид
Т.е. она состоит из m матриц с единицами по главной диагонали. Чтобы в одной строке такой матрицы остались хотя бы две единицы, необходимо оставить невычеркнутыми хотя бы два столбца. В другой строке должны быть не вычеркнуты хотя бы два обязательно других столбца. Итого, для четырех строк примера должны остаться невычеркнутыми восемь различных столбцов. Значит, вычеркнуть мы можем только четыре столбца (например, как выделено на изображении матрицы), а нам надо положить равными нулю шесть переменных! Тем самым, на базе лишь этих "нижних" уравнений образуются не менее двух уравнений с единственной переменной в левой части.
Т.к. произведение m ? n растет значительно быстрее суммы m + n, то с ростом параметров задачи указанное свойство усугубляется. Следовательно, мы с полным основанием может рассчитывать на принцип подстановки, как мы и делали в примере.
Однако программирование схемы Гаусса может оказаться не только менее трудоемко. Не следует забывать, что в процессе преобразования системы уравнений и последовательного получения значений переменных оперативно устанавливается как неразрешимость или неоднозначность, так и отрицательное решение.
Например, система (5.17) при реализации схемы Гаусса проходит следующие стадии преобразования.

Вычитание первой строки из последней и формирование разности на месте второй строки:

Вычитание пятой строки из третьей и размещение разности на месте четвертой строки:

Сложение шестой строки с пятой и расположение разности на месте пятой строки:

Получение нулевой строки в матрице достаточно для заключения о непригодности решения (в данном случае оно не существует).

Рассмотренная транспортная задача, без ограничения пропускной способности транспортных потоков, демонстрирует параллельный алгоритм ее решения. Программа, одинаковая для всех процессоров многопроцессорной ВС или станций локальной вычислительной сети, в основной своей части реализует выборку очередного ребра, исходящего из первоначально найденной вершины многогранника решений. Вдоль него ищется смежная вершина с меньшим значением целевой функции. Процессор, нашедший такую вершину, производит замену ранее исследовавшейся вершины и вынуждает все процессоры приступить к анализу ребер, исходящих из новой вершины. Так — до неудачного поиска вершины с меньшим значением целевой функции.

Использование в качестве источника загрузки процессоров общей уточняемой базы данных, в которой хранятся исследованные варианты поиска, позволяет выявлять еще не исследованные варианты и равномерно распределять нагрузку между процессорами.

Параллельное выполнение алгоритма

Предпочтительным способом распараллеливания здесь является распараллеливание по информации. Наиболее простая реализация его может быть основана на распределении между процессорами или станциями локальной сети строк матрицы S. И здесь самую простую реализацию предлагает принцип SPMD — "одна программа -- много потоков данных". Однако, как видно из примера, объем работ, связанных с разными строками, может быть весьма различным. Например, мы долго обрабатывали первую строку и быстро справились с такими строками, как 7, 8, 9. Значит, жесткое априорное распределение строк нежелательно. Оно обеспечивает неравномерную загрузку процессоров. Необходимо производить загрузку процессоров динамически, по мере их освобождения.
Здесь может быть эффективен тот же принцип, который используется при обработке баз данных, баз знаний и списковых структур.
Его реализация может быть следующей.
В соответствии с SPMD-технологией каждый процессор (станция локальной сети), участвующий в счете, обладает своим номером и знает количество процессоров. Множество строк матрицы S также упорядочено. Первоначально первый процессор выбирает для обработки и метит первую строку, второй — вторую и т.д.
По мере освобождения каждый процессор обращается к матрице S и выбирает первую из неотмеченных строк. Для согласованного обращения к S организуется синхронизация с помощью семафора методом взаимного исключения.
Сеть, в т.ч. транспортная, представляет собой параллельную структуру. Методы параллельного программирования предлагают эффективные средства для исследования сетей. Достоинством их является то, что сами эти методы допускают весьма простые способы распараллеливания. Это очень важно при обработке сетей большой размерности. Использование SPMD- технологии способствует эффективному применению многопроцессорных систем — внешних устройств персонального компьютера или множества станций локальной сети для решения задач высокой сложности.
Рассмотренные параллельные методы решения некоторых задач на транспортных сетях ориентированы на "прорыв в размерности", на выход на большие размерности задач, на задачи высокой, даже — экспоненциальной сложности. Только параллельные вычислительные системы могут решать такие задачи. Здесь очень важна концепция перспективных вычислительных средств: только ли разработка супер-ЭВМ призвана удовлетворить высокие требования по производительности? Не находятся ли на наших столах распределенные вычислительные комплексы РС, объединенные в локальные сети на основе современных, уже достаточно оперативных сетевых технологий? Именно для ответа на эти вопросы и должны критически перерабатываться и вновь создаваться параллельные алгоритмы решения сложных задач.

Параллельный алгоритм решения

Исследование плана параллельного решения и формирование алгоритма будем сопровождать примером, для проверки правильности заимствованным в [15]. Для краткости условия (5.3) и (5.4) опущены.
Пример.
Z=7x11+8x12+5x13+3x14+2x21+4x22+5x23+ +9x24+6x31+3x32+1x33+2x34 min (5.5)
при ограничениях
x11 + x12 + x13 + x14 = 11
x21 + x22 + x23 + x24 = 11
x31 + x32 + x33 + x34 = 8
x11 + x21 + x31 = 5 (5.6)
x12 + x22 + x32 = 9
x13 + x23 + x33 = 9
x14 + x24 + x34 = 7
Введем линейный массив переменных xij = yk, где k = (i - 1)n + j.
Исключим из рассмотрения последнее уравнение. Система уравнений граней (действительных и возможных) многогранника решений примет вид
y1 + y2 + y3 + y4 = 11
y5 + y6 + y7 + y8 = 11
y9 + y10 + y11 + y12 = 8 (5.7)
y1+y5+ y9=5
y2+y6+y10 = 9
y3+ y7+ y11 = 9
yk = 0, k = 1, 2, ... , 12.
Итак, на первом этапе задача свелась к выбору и анализу комбинаций по 12 - 6 = 6нулевых значений координат искомой вершины многогранника решений. Выполняя подстановку выбранной комбинации в (5.7), мы можем решить образовавшуюся систему шести уравнений с шестью неизвестными. Таким образом, мы сможем найти координаты некоторой вершины.
Комбинации по шесть нулевых значений координат ("комбинации нулей") следует выбирать так, чтобы не обратилась в нуль левая часть хотя бы одного уравнения (5.7), включая исключенное уравнение. Например, комбинация, где y1 = y2 = y3 = y4 = 0, недопустима.
Найдем дополнительные контрольные ограничения: чтобы решение было не отрицательным, необходимо, чтобы любое значение yk, k = 1, ... , m ? n, не превышало значение yk — величины правой части того уравнения, в котором оно участвует.
Тогда в нашем примере y1 min(11, 5) =y1 = 5, аналогично y2 y2 = 9, y3 y3 = 9, y4 y4 = 7, y5 y5 = 5, y6 y6 = 9, y7 y7 = 9, y8 y8 =7, y9 y9 = 5, y10 y10 = 8, y11 y11 = 8, y12
y12 = 7. Здесь при оценке y4, y8, y12учтено последнее уравнение в (5.6).
Воспользуемся векторной формой представления, чтобы подготовить удобные, нетрудоемкие матричные преобразования. А именно, наша система m + n - 1линейных уравнений-ограничений имеет вид

AY = B,

где A— нуль- единичная матрица, Y— столбец переменных, B— столбец свободных членов:

(5.8)

Тогда для нахождения хотя бы одного допустимого решения выберем допустимую комбинацию нулей по следующему алгоритму:

Положим l = 0.

Положим l := l + 1, yl = 0. Исключим из матрицы A столбец, соответствующий этой переменной.

Проверяем, появилась ли в A строка, содержащая только нулевые элементы, или обратилась ли в нуль левая часть исключенного уравнения. (Предполагаем, что все свободные члены уравнений больше нуля.) При положительном результате анализа выполняем шаг 5. В противном случае — следующий шаг.

Для каждой s-й строки A выделяем множество {ys}переменных, соответствующих единичным элементам. Проверяем:При отрицательном результате анализа (свободный член превышает сумму верхних оценок переменных) выполняем шаг 5. В случае успешной проверки 3 и 4 выполняем шаг 6.

Данный шаг выполняется, если испытываемое значение yl = 0 выбрано неудачно. Отменяем исключение столбца, соответствующего переменной yl, и выполняем шаг 2.

Фиксируем yl = 0, и если комбинация нулей сформирована не полностью, выполняем шаг 2.

Продолжим рассмотрение примера.

Полагаем y1 = 0. Это не приводит к нарушению оценок, указанных в алгоритме.

Полагаем y2 = 0. Это также не приводит к нарушению оценок.

Полагаем y3 = 0. Нулевые строки не появились. Однако в первой строке осталась единственная единица, соответствующая переменной y4. Т.к. y4= 7 < 11, отвергаем нулевое значение переменной.

Полагаем y4 = 0. Нулевые строки не появились, однако в первой же строке осталась единственная единица, соответствующая переменной y3. Т.к. y3 = 9 < 11, отвергаем и это значение.

Полагаем y5 = 0. Это не приводит к нарушению оценок.

Полагаем y6 = 0. В пятой строке остается единственная единица, соответствующая y10. Т.к. y10 = 8 < 9, отвергаем нулевое значение переменной.

Полагаем y7 = 0, что не приводит к нарушению оценок.

Значение y8 = 0 приводит к нарушению оценки во втором уравнении.

Значение y9 = 0 приводит к появлению нулевой строки.


Значение y10 = 0 не приводит к нарушению оценок.

Значение y11 = 0 также не приводит к нарушению оценок.

Итак, комбинация нулей найдена. Это отмеченные в (5.8) значения

y1 = 0, y2 = 0, y5 = 0, y7 = 0, y10 = 0, y11 = 0. (5.9)

Для нахождения других значений переменных необходимо решить систему уравнений на основе (5.8), после исключения нулевых столбцов



Найдем все строки матрицы A, содержащие не более одного единичного элемента. Это строки, определяющие компоненты решения y3

= 9, y6 = 9, y9 = 5.

Выполним подстановку, последовательно находя в столбцах найденных переменных единицы (не более одной) и корректируя правые части вычитанием найденных значений. Строки и столбцы, соответствующие найденным значениям переменных, исключаем из матрицы A.

Такой прием подстановки можно повторять до исчерпания уравнений, содержащих в левой части единственную переменную.

В нашем примере после подстановки найденных значений в уравнения 1, 2 и 3 получаем систему

В ней все уравнения имеют единственную переменную. Они определяют решение y4 = 2, y8 = 2, y12 = 3.

Таким образом, нам не пришлось пока воспользоваться методом Гаусса, но мы нашли допустимое решение Y0 = (0, 0, 9, 2, 0, 9, 0, 2, 5, 0, 0, 3), для которого выполняются ограничения задачи. Вектор Y0 определяет некоторую вершину многогранника допустимых решений, со значением целевой функции Z(Y0) = 141.

Примем следующий план решения, соответствующий рассмотренному ранее плану параллельного решения задач линейного программирования.

Для перебора всех смежных вершин необходимо в комбинации нулей, определивших вершину Y0, поочередно исключать одно значение yr = 0 (это определит одно из исходящих ребер) и оставшуюся систему решать совместно поочередно со всеми другими уравнениями вида ys = 0, не входящими в комбинацию нулей. Этим мы будем совершать перемещение в смежные вершины. Находя значение Z для каждого такого решения Y1 там, где оно существует, можно найти вершину с меньшим значением целевой функции. "Перебравшись" в эту вершину (приняв ее за Y0 ), мы можем продолжить анализ смежных ей вершин и т.д.


Решение задачи найдено в том случае, если после перебора всех смежных вершин не отыскивается вершина с меньшим значением целевой функции.

Продолжим рассмотрение примера.

Итак, (5.8) — исходный вид системы уравнений, (5.9) — комбинация нулей ("отсутствующие" столбцы в (5.7) выделены), (5.8) и (5.9) определяют вершину Y0.

Исключим из (5.9) уравнение y1 = 0, а оставшуюся систему, с учетом остальных нулей из комбинации (5.9), будем решать совместно с уравнениями

y3 = 0, y4 = 0, y6 = 0, y8 = 0, y9 = 0, y12 = 0. (5.10)

Значит, в (5.8) положим первоначально y3 = 0 вместо y1 = 0. Левая часть шестого уравнения (последняя строка матрицы А) обратилась в нуль.

Положим y4 = 0 вместо y1 = 0. Получим систему

Из нее, как и ранее, за два шага подстановки находим y3 = 9, y6 = 9, y9 = 5, а затем — y1 = 2, y8 = 2, y12 = 3.

Таким образом, найдено новое допустимое решение Y1 = (2, 0, 9, 0, 0, 9, 0, 2, 5, 0, 0, 3). Однако Z(Y1) =149 > 141. Найденную вершину отвергаем. Вместе с тем, т.к. мы нашли вершину "на другом конце" анализируемого ребра, то и анализ этого ребра прекращаем.

Приступаем к анализу следующего ребра, исключив из (5.9) уравнение y2 = 0. Оставшуюся систему, с учетом остальных нулей из (5.9), будем решать совместно с теми же уравнениями (5.10).

Положим в (5.8) y3 = 0 вместо y2 = 0. Последняя строка матрицы A стала нулевой.

Замена y4 = 0 вместо y2 = 0 приводит к системе

На ее основе находим новый вектор — допустимое решение Y1 = (0, 2, 9, 0, 0, 9, 0, 2, 5, 0, 0, 3). Однако Z(Y1) = 151 > 141. Найденную вершину также отвергаем. Ребро исследовано полностью.

Исключим из (5.9) уравнение y5 = 0, а оставшуюся систему, с учетом остальных нулей из (5.9), будем решать совместно с теми же уравнениями (5.10).

Положим в (5.8) y3 = 0 вместо y5 = 0. Последняя строка матрицы A обратится в нуль.

Положим y4 = 0 вместо y5 = 0. В первом уравнении не выполняется ограничение по y3 (y3 = 9).

Положим y6 = 0 вместо y5 = 0. Пятая строка A обратилась в нулевую.

Положим y8 = 0 вместо y5 = 0.


Получим систему уравнений

Находим y3 = 9, y6 = 9 и после подстановки — y4 = 2, y5 = 2. Вновь выполняем подстановку, находим y9 = 3, и после следующей подстановки y12 = 5.

Итак, получена вершина Y1 = (0, 0, 9, 2, 2, 9, 0, 0, 3, 0, 0, 5). Т.к. Z(Y1) = 119 < 141, полагаем Y0 := Y1 и начинаем пробу возможных перемещений вдоль ребер из найденной вершины многогранника решений в вершину с меньшим значением целевой функции:

Запишем вновь аналогично (5.8) и (5.9) систему уравнений, решением которой является вершина Y0, отметив в ней "отсутствующие" столбцы:

(5.11)

Находим

y1 = 0, y2 = 0, y7 = 0, y8 = 0, y10 = 0, y11 = 0. (5.12)

Начнем движение по ребрам из данной вершины. Для этого будем исключать из (5.12) одно из уравнений, а оставшуюся систему будем решать совместно с не вошедшими в (5.12) уравнениями:

y3 = 0, y4 = 0, y5 = 0, y6 = 0, y9 = 0, y12 = 0. (5.13)

При этом надо учесть, что могут формироваться ранее исследованные комбинации нулей. (Комбинации нулей удобно метить индексным кодом, который следует запоминать для исключения повторного анализа.)

Положим в (5.13) y3 = 0 вместо y1 = 0. Последняя строка матрицы A станет нулевой.

Замена y1 = 0 уравнением y4 = 0 приводит к системе

Решаем с помощью подстановок, находим Y1 = (2, 0, 9, 0, 2, 9, 0, 0, 3, 0, 0, 5). Т.к. Z(Y1) = 127 > 119, найденную вершину отвергаем.

Примечание. Нам вновь не пришлось воспользоваться схемой Гаусса. По-видимому, вид уравнений и вхождение каждой переменной не более чем в два уравнения позволяют довольствоваться простой подстановкой. Ниже мы исследуем это подробнее.

Переходим к другому ребру, заменяя в (5.12) уравнение y2 = 0 уравнениями из (5.13).

Замена y3 = 0 вместо y2 = 0 приводит к тому, что последняя строка матрицы A становится нулевой.

Замена y4 = 0 вместо y2 = 0 приводит к системе уравнений

Находим с помощью подстановок Y1 = (0, 2, 9, 0, 4, 7, 0, 0, 1, 0, 0, 7). Т.к. Z(Y1) = 127 > 119, найденную вершину отвергаем и переходим к анализу следующего ребра.

Замена y3 = 0 вместо y7 = 0 приводит к тому, что в первом уравнении (9.25) не выполняется условие по ограничению y4 (y4 = 7).


Замена y4 = 0 вместо y7 = 0 приводит к тому, что в первом же уравнении (9.25) не выполняется условие по ограничению y3 (y3 = 9).

Замена y5 = 0 вместо y7 = 0 приводит к системе

Находим Y1 = (0, 0, 7, 4, 0, 9, 2, 0, 5, 0, 0, 3). Однако Z(Y1) = 129 > 119.

Переходим к анализу следующего ребра, поочередно заменяя уравнениями из (5.13) уравнение y8 = 0 из (5.11).

Замена y3 = 0 вместо y8 = 0 приводит к образованию последней нулевой строки матрицы A.

Замена y4 = 0 вместо y8 = 0 приводит к тому, что в первом уравнении не выполняется условие по ограничению y3 (y3 = 9).

Замена y5 = 0 вместо y8 = 0 приводит к системе

Находим Y1 = (0, 0, 9, 2, 0, 9, 0, 2, 5, 0, 0, 3). Т.к. Z(Y1) = 141 > 119, найденную вершину отвергаем.

Переходим к анализу следующего ребра, поочередно заменяя уравнениями из (5.13) уравнение y10 = 0 из (5.11).

Замена y3 = 0 вместо y10 = 0 приводит к тому, что в первом уравнении (5.11) не выполняется условие по ограничению y4 (y4 = 7).

Замена y4 = 0 вместо y10 = 0 приводит к тому, в первом же уравнении (5.11) не выполняется условие по ограничению y3 (y3 = 9).

Замена y5 = 0 вместо y10 = 0 приводит к тому, что во втором уравнении (5.11) не выполняется условие по ограничению y6 (y6= 9).

Замена y6 = 0 вместо y10 = 0 приводит к тому, что во втором же уравнении (5.11) не выполняется условие по ограничению y5 (y5 = 5).

Замена y9 = 0 вместо y10 = 0 приводит к системе

Находим Y1 = (0, 0, 9, 2, 5, 6, 0, 0, 0, 3, 0, 5). Т.к. Z(Y1) = 104 < 119, "перемещаемся" в найденную вершину с меньшим значением целевой функции.

Новая вершина характеризуется системой уравнений

y1 = 0, y2 = 0, y7 = 0, y8 = 0, y9 = 0, y11 = 0. (5.14)

Перепишем систему (5.11), выделив "отсутствующие" столбцы, вследствие (5.14):

(5.15)

После исключения одного из уравнений (5.14) оставшаяся система (5.15), (5.14) будет решаться совместно с одним из уравнений

y3 = 0, y4 = 0, y5 = 0, y6 = 0, y10 = 0, y12 = 0 (5.16)

Замена y1 = 0 на y3 = 0 приводит к появлению (последней) нулевой строки матрицы A.


Замена y4 = 0 вместо y1 = 0 приводит к системе



Отсюда Y1 = (2, 0, 9, 0, 3, 8, 0, 0, 0, 1, 0, 7). Т.к. Z(Y1) = 114 > 104, исследуем следующее ребро, исключив в системе (5.14) уравнение y2 = 0 и заменяя его последовательно уравнениями из (5.16).

Замена y4 = 0 вместо y2 = 0 приводит к системе

Находим Y1 = (0, 2, 9, 0, 5, 6, 0, 0, 0, 1, 0, 7). Т.к. Z(Y1) = 114 > 104, исследуем следующее ребро, исключив в системе (5.14) уравнение y7 = 0 и заменяя его последовательно уравнениями из (5.16).

Замена y3 = 0 вместо y7 = 0 приводит к тому, что в первом уравнении (9.29) не выполняется условие по ограничению y4 (y4 = 7).

Замена y4 = 0 вместо y7 = 0 приводит к тому, что в первом же уравнении (9.29) не выполняется условие по ограничению y3 (y3= 9).

Замена y5 = 0 вместо y7 = 0 приводит к формированию нулевой (четвертой) строки матрицы A.

Замена y6 = 0 вместо y7 = 0 приводит к формированию нулевой (пятой) строки матрицы A.

Замена y10 = 0 вместо y7 = 0 приводит к тому, что в третьем уравнении (5.15) не выполняется условие по ограничению y12

(y12 = 7).

Замена y12 = 0 вместо y7 = 0 приводит к системе

Находим Y1 = (0, 0, 4, 7, 5, 1, 5, 0, 0, 8, 0, 0). Т.к. Z(Y1) = 104 и это не меньше уже полученной оценки, исследуем следующее ребро, исключив в системе (5.14) уравнение y8 = 0 и заменяя его последовательно уравнениями из (5.16).

Замена y3 = 0 вместо y8 = 0 приводит к образованию нулевой (шестой) строки матрицы A.

Замена y4 = 0 вместо y8 = 0 приводит к тому, что в первом уравнении (5.15) не выполняется условие по ограничению y3 (y3 = 9).

Замена y5 = 0 вместо y8 = 0 приводит к образованию нулевой (четвертой) строки матрицы A.

Замена y6 = 0 вместо y8 = 0 приводит к тому, что в пятом уравнении (5.15) не выполняется условие по ограничению y10 (y10= 8).

Замена y10 = 0 вместо y8 = 0 приводит к тому, что в третьем уравнении (5.15) не выполняется условие по ограничению y12 (y12 = 7).

Замена y12 = 0 вместо y8 = 0 приводит к системе

Ее решение Y1 = (0, 0, 9, 2, 5, 1, 0, 5, 0, 8, 0, 0) определяет значение Z(Y1) = 134 > 104.


Продолжаем перебор по следующему ребру.

Замена y3 = 0 вместо y9 = 0 приводит к образованию нулевой (шестой) строки матрицы A.

Замена y4 = 0 вместо y9 = 0 приводит к тому, что в первом уравнении (5.15) не выполняется условие по ограничению y3 (y3 = 9).

Замена y5 = 0 вместо y9 = 0 приводит к тому, что во втором уравнении (5.15) не выполняется условие по ограничению y6 (y6= 9).

Замена y6 = 0 вместо y9 = 0 приводит к тому, что во втором же уравнении (5.15) не выполняется условие по ограничению y5 (y5 = 5).

Замена y10 = 0 вместо y9 = 0 приводит к системе



Ее решение Y1 = (0, 0, 9, 2, 2, 9, 0, 0, 3, 0, 0, 5) определяет значение Z(Y1) = 119 > 104.

Приступаем к анализу следующего ребра, исключая в (5.14) уравнение y11 = 0 и заменяя его последовательно уравнениями из (5.16).

Замена y3 = 0 вместо y11 = 0 приводит к тому, что в первом уравнении (5.15) не выполняется условие по ограничению y4 (y4 = 7).

Замена y4 = 0 вместо y11 = 0 приводит к тому, что в первом уравнении (5.15) не выполняется условие по ограничению y3 (y3 = 9).

Замена y5 = 0 вместо y11 = 0 приводит к тому, что во втором уравнении (5.15) не выполняется условие по ограничению y6 (y6 = 9).

Замена y6 = 0 вместо y11 = 0 приводит к тому, что во втором же уравнении (5.15) не выполняется условие по ограничению y5 (y5 = 5).

Замена y10 = 0 вместо y11 = 0 приводит к системе

(5.17)

Система не имеет решения, т.к. ранг матрицы системы не равен рангу расширенной матрицы.

Примечание. В несложном примере это легко обнаружить: вторая строка матрицы равна сумме четвертой и пятой строк, что противоречит соотношению между соответствующими свободными членами, 9 + 5

11. По-видимому, это говорит в пользу применения схемы Гаусса. В противном случае мы должны контролировать последовательно получаемые решения на удовлетворение тем соотношениям, которые в его получении не участвовали. Так, из четвертого и пятого уравнений имеем y5 = 5, y6 = 9. Но в соответствии со вторым уравнением y5 + y6 = 11. В то же время, совершая подстановку во второе уравнение, мы получаем нулевую левую часть, т.е.


нулевую строку матрицы A, что опять говорит в пользу подстановок!

Замена y12 = 0 вместо y11 = 0 приводит к системе

Ее решение Y1 = (0, 0, 4, 7, 5, 6, 0, 0, 0, 3, 5, 0) определяет значение целевой функции Z(Y1) = 89 < 104.

Полагаем Y0 := Y1. Теперь мы должны перемещаться по ребрам из вновь найденной вершины в поисках вершины с еще меньшим значением целевой функции. Придется перебрать до 6 ? 6 = 36 вариантов такого перемещения. Однако, достигнув ответа задачи в [15], положимся на его правильность и прекратим рассмотрение примера.

Постановка задачи и планы решения

Пусть [15] в пунктах A1, A2, ... ,Am производят некоторый однородный продукт в объеме ai (i=1, 2, ... , m) единиц. В пунктах B1, B2, ... ,Bn этот продукт потребляется в объеме bj
( j=1, 2, ... , n) единиц. Из каждого пункта производства {Ai} возможна транспортировка в любой пункт потребления Bj. Транспортные издержки} по перевозке из пункта Aiв пункт Bjединицы продукции равны cij (i=1, ... , m; j=1, ... , n).
Необходимо найти такой план перевозок, при котором запросы всех потребителей полностью удовлетворены, весь продукт из пунктов производства вывезен и суммарные транспортные издержки минимальны.
Пусть xij— количество продукта, перевозимого из пункта Aiв пункт Bj. Требуется найти значение переменных (перевозок) xij 0 (i = 1, 2, ... , m; j = 1, 2, ... , n), удовлетворяющих

(5.1)

при ограничениях

(5.2)

при условии неотрицательности
xij 0 (5.3)
и баланса

(5.4)

Как известно, условие баланса приводит к линейной зависимости уравнений в системе (5.2), ранг ее матрицы равен m+n-1.
Сформулируем задачу линейного программирования в канонической постановке, исключив из (5.2) одно уравнение. При этом мы считаем, что условие баланса (5.4) оказывает влияние на корректность постановки задачи и учтено при этой постановке. Исключенное уравнение будем использовать также для контроля получаемого решения.
Следуя плану параллельного решения задачи линейного программирования и учитывая, что оптимальное решение находится хотя бы в одной из вершин многогранника допустимых решений, образуемого ограничениями и условиями, сформируем это множество граней. В его состав войдут m+n-1 выделенных уравнений-ограничений и m ? n равенств нулю переменных на основе неотрицательности решения. Выбирая из этой системы по m ? n уравнений с обязательным участием всех выделенных уравнений-ограничений и решая их совместно, мы можем находить вершины многогранника решений.
Так мы можем реализовать метод прямого перебора. Количество вариантов составляет Cm ? nm ? n - (m + n - 1) . Это — количество различных способов приравнивания нулю m ? n-(m+n-1) переменных из их общего числа m ? n.
Мы можем реализовать и аналог симплекс-метода, найдя первоначально некоторую вершину, а затем перемещаясь по ребрам в одну из смежных вершин с большим значением целевой функции, пока это возможно.

Пусть dij — пропускная способность коммуникации (i, j), что порождает ограничение
xij dij
(5.18)
для всех i, j.
Тогда важная в практическом отношении задача заключается в минимизации (5.1) — целевой функции Z при ограничениях (5.2), (5.3), (5.4) и (5.18). Очевидно, что для разрешимости T -задачи должны выполняться условия

(5.19)

(5.20)

Как видим, данную задачу тоже можно решать прямым перебором вершин R с учетом резко увеличившегося числа уравнений его границ: их число, с учетом линейной зависимости, составляет теперь n+m-1+2(m? n). С учетом границ на основе условий неотрицательности решения, общее число испытываемых систем линейных уравнений составит C2(m ? n)m ? n - (m + n - 1).
Однако при этом переборе мы будем исследовать явно несовместимые варианты компоновки систем — а именно, варианты, включающие пары уравнений вида xij=0 и xij=dij. Тогда поступим иначе.
Сначала будем выбирать комбинации переменных, участвующих в формировании указанных систем линейных уравнений. Всех таких комбинаций будет Cm ? nm ? n - (m + n - 1). После выбора очередной комбинации переменных определим комбинацию их значений — 0 или значение пропускной способности. Таких комбинаций для выбранного набора m ? n - (m + n) - 1 переменных будет 2m ? n - (m + n - 1) .
Таким образом, общее число испытываемых систем линейных уравнений составит Cm ? nm ? n - (m + n - 1) ? 2m ? n - (m + n - 1) .
Воспользуемся и здесь параллельным аналогом симплекс-метода, найдя первоначально некоторую вершину многогранника решений, а затем пытаясь "переместиться" в смежную вершину с меньшим значением целевой функции.
Сделаем важное замечание. Будем считать, что если вдоль прямой, отрезком которой является исходящее из вершины L ребро, найдена смежная вершина M, то на этой же прямой, "в другую сторону" от L, нет смежных вершин. Т.е. одна прямая может связывать не более двух вершин многогранника решений. Предположим, что три вершины M, L, N лежат на одной прямой. Т.к. L — вершина, то существует хотя бы еще одно исходящее из нее ребро. Пусть оно соединяет L с вершиной K. Тогда построим плоскость, проходящую через три точки M, N, K, т.е. через точку K и прямую MN, которой принадлежит точка L. Плоскость поглотила как точку L, так и новое ребро, существование которого мы предположили.
Это означает, что если мы нашли смежную вершину "с одной стороны" по прямой, отрезком которой является исходящее ребро, то искать смежную вершину "с другой стороны" по этой же прямой не следует.
Этим предположением мы пользовались в предыдущем разделе, прекращая дальнейший поиск других смежных вершин вдоль прямой в случае, если одна такая вершина оказывается найденной. Здесь же это замечание, в частности, означает, что если мы нашли смежную данной вершину со значением xij = 0 ( xij = dk ), то испытывать значение xij = dk ( xij = 0 ) не следует. Т.е., как и ранее, мы вдоль каждого исходящего ребра будем искать единственную смежную вершину.

и ранее, линейное множество переменных

Введем, как и ранее, линейное множество переменных и сформулируем задачу:
Z = 2y1 + 3y2 + 3y3 + 2y4 + 2y5 + y6 min
при ограничениях
y1 + y2 + y3 = 12
y4 + y5 + y6 =10 (5.21)
y1+ y4 =7
y2 + y5 =7
y3 + y6 = 8
и при условии
0 y1 4, 0 y2 4, 0 y3 5, 0 y4 4, 0 y5
4, 0 y6 3. (5.22)
Сформируем ограничения каждой переменной: y1 = min{12, 7, 4} = 4, аналогично y2 = 4, y3 = 5, y4 = 4, y5 = 4, y6 = 3. Исключим из рассмотрения последнее уравнение (5.21) и запишем уравнения всех потенциальных граней на основе (5.22):
y1 + y2 + y3 = 12
y4 + y5 + y6 = 10(5.23)
y1 + y4 = 7
y2 + y5 = 7
y1 = 0; y1 = 4
y2 = 0; y2 = 4
y3= 0; y3 = 5 (5.24)
y4 = 0; y4 = 4
y5 = 0; y5 = 4
y6 = 0; y6 = 3
Начнем перебор систем по шесть граней в поисках координат одной из вершин многогранника решений. В каждой такой системе должны присутствовать все уравнения (5.23) и два уравнения с разными переменными из (5.24).
Для формирования первой системы уравнений пробуем добавить к (5.23) уравнение y1 = 0. В результате в третьем уравнении не выполняется ограничение по y4 (y4 = 4).
Пробуем вариант y1 = 4. Совершив подстановку, убеждаемся, что он не приводит к подобному противоречию.
Полагаем y2 = 0. В первом уравнении не выполняется ограничение по y3 (y3 = 5).
Полагаем y2 = 4. Получаем и решаем систему уравнений
y1 + y2 + y3 = 12
y4 + y5 + y6 = 10
y1 + y4 = 7
y2 + y5 = 7
y1= 4
y2 = 4.
Находим Y = (4, 4, 4, 3, 3, 4). Однако данная точка не является вершиной многогранника решений, т.к. y6 = 4 противоречит условию (5.22).
Испытываем уравнение y3 = 0. В первом уравнении нарушается ограничение по y1 + y2 (y1 + y2 = 8 < 12).
Испытываем уравнение y3 = 5. Решаем систему уравнений
y1 + y2 + y3 = 12
y4 + y5 + y6 = 10
y1 + y4 = 7
y2 + y5 = 7
y1 = 4
y3 = 5.
Находим Y0 = (4, 3, 5, 3, 4, 3). Решение удовлетворяет условиям задачи, следовательно, найденная точка — вершина многогранника решений. Находим значение целевой функции Z(Y0) = 49.
На основе (5.23) и (5.24) выпишем уравнения всех граней, которым удовлетворяет вершина Y0, т.е.

в стек первую строку матрицы

Продолжим исследование приведенной выше сети.

Заносим в стек первую строку матрицы S. Находим первый нуль после обязательного нуля в первой позиции. Этот нуль указывает, что каналы 1 и 2 взаимно независимы (параллельны). Складываем логически строки, соответствующие каналам 1 и 2. Получаем новую строку s1 в вершине стека
Она содержит нули правее позиции 2. Это говорит о том, что 1 и 2 не исчерпывают ПМВНК.

Находим первый нуль правее позиции 2 — нуль в позиции 3. Складываем логически s2 = s1 "3". Получаем новую строку в вершине стека и весь стек в виде
Строка в вершине стека содержит нули только в тех позициях, которые соответствуют образующим ее каналам 1, 2, 3. Это означает, что мы нашли ПМВНК {1, 2, 3}, т.е. некоторый разрез сети. Минимальный поток, проходящий через него, составляет d1 + d2 + d3.

Исключаем из стека строку s2 и в строке s1 испытываем следующий нуль правее позиции 2. Это нуль в позиции 4. Формируем новую вершину стека s3 = s1 "4".
Строка s3 содержит нули не только в позициях 1, 2, 4. Первый такой нуль правее позиции 4 — в позиции 7.
Формируем новую вершину стека s4 = s3 "7". Стек принимает вид
Строка s4 содержит нули только в позициях, соответствующих каналам, "участвующим" в ее формировании. Значит, найдено еще одно ПМВНК {1, 2, 4, 7}. Оно определяет разрез сети с пропускной способностью d1 + d2 + d4 + d7.

Исключаем s4 из стека. Следующий испытываемый нуль в строке s3 занимает позицию 8. Формируем новую вершину стека s5 = s3 "8".
Строка s5 содержит нули только в позициях 1, 2, 4, 8. Следовательно, найдено ПМВНК {1, 2, 4, 8} с пропускной способностью d1 + d2 + d4 + d8.

Исключаем s5 из стека. Находим, что в s3 все нули исследованы. Исключаем s3 из стека. В s1 следующий нуль, подлежащий испытанию, занимает позицию 7. Формируем новую вершину стека — строку s6 = s1 "7".
Строка s6 не содержит нулей правее позиции 7. Исключаем s6 из стека.

Следующий испытываемый нуль в s1 занимает позицию 8.

Параллельное программирование

Алгоритм. Пример

Выше фактически уже описан алгоритм нахождения хотя бы одной вершины многогранника допустимых решений. Сведем вместе все необходимые построения.
Алгоритм.

Определим направление возрастания целевой функции и выделим грани многогранника допустимых решений, образующие верхнюю (нижнюю) его поверхность. Дополним ее возможными гранями — координатными плоскостями.

Составим матрицу S косинусов углов между всеми нормалями к действительным и возможным граням сформированной поверхности многогранника допустимых решений.

Если число r действительных граней верхней (нижней) поверхности не меньше n — размерности задачи, выполняем первый этап алгоритма, исключив из рассмотрения строки и столбцы матрицы S, соответствующие координатным плоскостям.

Этот пункт является общим для первого и второго этапов. Выбрав произвольно грань или организовав перебор всех граней, или организовав параллельный анализ всех граней, выберем в соответствующей этой грани строке матрицы S n максимальных косинусов. В этой последовательности косинусов, кроме максимального косинуса угла между нормалью выбранной грани и ею же самой, не должно быть косинусов, равных 1 или -1. Таким образом, окажутся выделенными n возможных образующих некоторой вершины многогранника допустимых решений.

Решаем совместно уравнения выделенных граней.

Если решение существует и оно неотрицательно, произведем анализ: удовлетворяет ли найденная точка всем ограничениям задачи? Если удовлетворяет, точка действительно является вершиной многогранника. В противном случае необходимо продолжить анализ граней, то есть строк матрицы S.

Если перебор всех строк матрицы S не привел к успеху на первом этапе выполнения алгоритма, переходим ко второму этапу, введя в рассмотрение координатные плоскости, т.е. начинаем анализ матрицы в полном объеме. Если успех не был достигнут на втором этапе, то, как указано ниже, можно испытать удачу на другой — нижней (верхней) поверхности многогранника допустимых решений. Ведь важно найти хоть какую-то вершину, пусть не столь близкую к вершине-решению.
Если мы и теперь не достигли успеха…

В рассматриваемом примере верхнюю поверхность (где следует искать решение) образуют грани (6.6). Поскольку переименование малого количества граней в соответствии с (6.7) не имеет смысла, составим для этих граней и их нормалей таблицу, включающую матрицу косинусов углов между нормалями. Соответствующие косинусы считаем по (6.9) и (6.10), таблицу строим по образу таблицы 6.1. Матрица S в таблице выделена.

Реализуем первый этап алгоритма поиска вершины, исключив из рассмотрения три последние строки и столбцы.

Выберем грань q1. Максимальные косинусы соответствующей (первой) строки матрицы S указывают на систему граней {q1, q2, q3}. Решаем уравнения граней совместно и проверяем решение на выполнение всех неиспользованных ограничений задачи. Получаем вершину E(13, 8, 4).

Таблица 6.4. ГраньНормальN1 N2N3N4 N5 N7 N8 N9

q1	N1	l	0,59	0,59	0,067	0,171	0,026	0,09	-0,99
q2	N2	0,59	1	0,9	-0,43	-0,29	-0,56	0,625	-0,56
q3	N3	0,59	0,9	1	-0,25	-0,125	-0,28	0,46	-0,84
q4	N4	0,067	-0,43	-0,25	1	0,99	-0,16	-0,975	-0,16
q5	N5	0,171	-0,29	-0,125	0,99	1	-0,27	-0,92	-0,27
q7	N7	0,026	-0,56	-0,28	-0,16	-0,27	1	0	0
q8	N8	0,09	0,625	0,46	-0,975	-0,92	0	1	0
q9	N9	-0,99	-0,56	-0,84	-0,16	-0,27	0	0	1

Выберем грань q2. Максимальные косинусы второй строки матрицы указывают на систему граней {q2, q3, q1}, что соответствует уже найденной вершине.

Для грани q3 получаем ту же систему образующих граней, т.е. ту же вершину E.

По строке табл. 6.4 (матрицы S), соответствующей q4, находим систему {q1, q4, q5}, решением которой является вершина L{6, 10, 4}.

Анализируя строку грани q5, вновь получаем ту же вершину.

Таким образом, мы добились успеха без рассмотрения координатных плоскостей. Однако для полноты анализа исследуем матрицу S полностью.

Анализ строк 1, 3, 4, 5 порождает те же результаты. Максимальные косинусы второй строки, соответствующей грани q2, указывают на систему {q2, q3, q8}. Решаем уравнения совместно и проверяем выполнение всех неиспользованных ограничений.


Получаем вершину D(6, 0, 2).

Со строкой, соответствующей q7, начинаются трудности, обусловленные следующими факторами:

Координатная плоскость — возможная, но не действительная грань.

Именно нормали к координатным плоскостям образуют угол . Нулевое значение этого косинуса неоднозначно соответствует углам и . Поэтому невозможно правильно упорядочить углы по неубыванию, используя отрицательные и нулевые значения косинусов.

Если, не зная, что делать с нулями, упорядочить только косинусы углов между нормалью к q7 (x = 0) и нормалями к граням-границам, то первые три косинуса невозрастающей последовательности укажут на грани {q1, q4, q7}. Однако точка (0, 11, 4) — решение этой системы — не является вершиной многогранника R, так как не удовлетворяет ограничению q6.

Для возможной грани q8, также не обращая внимание на нули, находим систему {q2, q3, q8}, решением которой является вершина D(6, 0, 2). (По-видимому, углы между нормалями не вышли из диапазона [0, ]).

По последней строке, соответствующей возможной грани q9, находим систему {q4, q5, q9}, решением которой является вершина K(10, 10, 0).

(Неслучайность успеха в последних трех случаях нуждается в обосновании.)

Отметим, что нет гарантии получения всех вершин поверхности. Ведь группируя вместе грани, мы отдаем предпочтение вершинам с "пологими" склонами, выбирая максимальные значения косинусов. В частности, мы ни разу здесь не получили вершину F(17, 8, 0), в которой целевая функция принимает максимальное значение. Так что второй этап решения задачи ЛП неизбежен. Более того, необходимо не качественное, а аналитическое доказательство того, что рассмотренным путем при выполнении определенных условий будет получена хотя бы одна вершина многогранника R допустимых решений задачи. То есть необходимо доказать теорему существования.

Оценка сложности

Алгоритм поиска вершины многогранника допустимых решений предполагает ряд этапов.

Определение верхней (нижней) поверхности многогранника. Он заключается в проверке выполнения всех ограничений для точки начала координат. Сложность этого этапа можно оценить как O(nm). Число r граней-границ, образующих одну поверхность, не превышает m - 1,
r m - 1 (6.12)

Нахождение матрицы S косинусов углов между нормалями к действительным и возможным граням поверхности. Число таких косинусов для симметричной матрицы с учетом известных углов между осями координат составляет

(6.13)

Каждый косинус отыскивается в результате скалярного произведения единичных векторов нормалей, имеющего сложность O(6n). С учетом (6.12) можно оценить сложность алгоритма нахождения матрицы S как
O(3m2n + mn2). (6.14)

Выделение n максимальных косинусов в каждой строке матрицы S. Сложность этой операции упорядочения по одной строке можно оценить как
O((m + n)2) (6.15)

Наконец, для выделенных граней необходимо решить систему n линейных уравнений, соответствующих этим граням. Сложность алгоритма такого решения составляет O(n3). Общая сложность выполнения этого этапа для всех строк составляет
O(mn3 + n4). (6.16)

Как видим, сложность нахождения вершины (точнее, всех возможных вершин) полиномиальная. Сумма степеней основных параметров n и m в составе членов полинома не превышает четырех.
В заключение отметим, что наметился общий прием распараллеливания решения задач оптимизации. Это не просто прием распараллеливания вычислений. Он определяет стратегию коллективного поведения компьютеров вычислительной системы или вычислительной сети при совместном решении задачи.
Алгоритм решения задачи предполагает, на разных этапах или глобально, варианты поиска промежуточных или окончательных решений. Компьютеры "расходятся" по отдельным вариантам поиска. Отдельный компьютер может достичь или не достичь успеха, реализуя стратегию "проб и ошибок". Тот компьютер, что достиг успеха, оперативно извещает другие компьютеры, которые прерывают свои действия. Все компьютеры используют успех одного для продолжения выполнения задачи.
Такой прием используется для поиска смежной вершины (по разным ребрам) с "лучшим" значением целевой функции при решении задачи ЛП. Такой же прием может применяться и для нахождения опорного плана решения этой же задачи. Ведь грани верхней (нижней) поверхности многогранника допустимых решений могут распределяться между компьютерами. Компьютер может для взятой на обработку грани найти все косинусы между ее нормалью и нормалями с другими гранями, и здесь не следует бояться повторения счета отдельных косинусов на разных компьютерах. Затем компьютер может выбрать n максимальных косинусов и проверить выделенную таким образом точку. Как только вершина найдена, работа других компьютеров по аналогичному поиску может быть прервана.
Однако возможно, и это должно быть исследовано статистически, что себя оправдает такая стратегия, когда в результате нахождения нескольких вершин в качестве опорного плана будет взято решение, обеспечивающее "лучшее" значение целевой функции.
Все сказанное наилучшим образом согласуется с SPMD-технологией "одна программа — много потоков данных ".
Вместе с тем, отметим, что здесь предлагается "инженерное" решение задачи на основе ее "физического смысла". Работа по обоснованию и строгому доказательству основных положений должна быть продолжена. Скорее всего, мы наблюдаем интересные свойства выпуклого многогранника допустимых решений задачи ЛП, не всегда умея их строго доказать.

Основные предположения

Определение. Назовем плоскость в n-мерном пространстве образующей вершины A выпуклого многогранника R допустимых решений задачи ЛП, если ее уравнение входит в состав системы n линейных уравнений границ многогранника R, решением которой является точка A.
В общем случае каждая вершина многогранника R имеет не менее n образующих плоскостей. Часть из них может совпадать с координатными плоскостями.
Изменим обозначение плоскостей-граней, образующих исследуемую далее верхнюю (нижнюю) поверхность многогранника R:
Qверхн (Qнижн) ={p1, p2,... , pr, pr+1, ... ,pr+n}. (6.7)
Здесь , j = 1, ... , r, — действительные плоскости грани, pr+k = qm+k, k = 1, ... , n, — координатные плоскости.
Сменим обозначение и коэффициентов уравнений плоскостей, выделив совокупность всех граней многогранника R — действительных и возможных, образующих исследуемую (верхнюю или нижнюю) поверхность:
p1 = d11 x1 + d12 x2 +... + d1n xn = 0
p2 = d21 x1 + d22 x2 +... + d2n xn = 0
...
pr = dr1 x1 + dr2 x2 +... + dr n xn = 0 (6.8)
pr+1 = x1 = 0
...
pr+n = xn = 0.
Найдем координаты единичных векторов нормалей Nj, j = 1,... , n+r, к плоскостям (6.8):

(6.9)

где

(6.10)

Тогда косинус угла между нормалями к двум граням верхней (нижней) поверхности R вычисляется как результат скалярного произведения единичных векторов нормалей:

(6.11)

Выскажем гипотезу, которая является основой теоремы существования:
Если плоскости pj и pq совместно не являются образующими какой-либо вершины верхней (нижней) поверхности выпуклого многогранника R допустимых решений задачи ЛП, а их нормали Nj и Nq образуют "угол" , то существует плоскость pl с нормалью Nl, совместно с pj являющаяся образующей некоторой вершины этой же поверхности и такая, что "угол" ? между нормалями Nj и Nl меньше угла . (? < ).
Слово "угол" берем в кавычки в связи с тем, что любой угол измеряется в плоскости и видеть его мы можем в двух- и трехмерном пространстве.
В общем случае n-мерного пространства мы можем судить о величине угла по его косинусу, который отыскивается как результат скалярного произведения единичных векторов.
Отсюда следует, что геометрически мы можем продемонстрировать верность гипотезы в двух- и трехмерном пространстве. В общем же случае доказательство ее справедливости должно быть аналитическим.

Итак, поясним высказанное предположение "плоским" рис. 6.4.


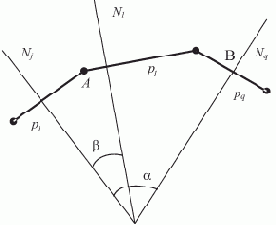
Рис. 6.4.  Соотношение углов между нормалями смежных граней

Выделим произвольную вершину A многогранника R. Она "окружена" образующими ее гранями (на плоскости — ребрами). Пусть pj — одна из них. Любая грань, не являющаяся образующей вершины A, например — грань (ребро) pq, добавляет угол излома поверхности в угол наклона ? ее нормали Nq. Точка пересечения pj и pq находится вне R. Тогда должна существовать образующая эту же вершину грань (ребро) pl, нормаль к которой Nl имеет меньший угол наклона, ? < .

Представим (рис. 6.5) аналогичную картину в трехмерном пространстве.


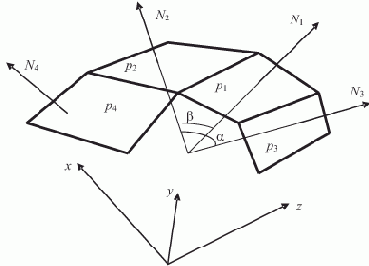
Рис. 6.5.  Соотношение углов между нормалями в трёхмерном пространстве

Пусть p2 и p3 не являются смежными на данной поверхности многогранника R, то есть не имеют общего ребра и, следовательно, совместно не являются образующими какой-либо вершины. Тогда существует одна или более разделяющих их граней, здесь, например — грань p1, нормаль к которой N1 образует с нормалью N2 угол ? меньший угла — угла между нормалями N2 и N3.

Минуя формальное и строгое доказательство, продолжим пояснение гипотезы на качественном уровне.

Грани p1 и p2 являются образующими двух вершин A и B. Для гарантии смежности этих граней, то есть того, что они совместно являются образующими какой-то вершины, можно в основу выбора такой вершины положить минимальный угол между нормалями к ним. То есть будем считать, что если для фиксированной грани pj найден минимальный из углов между нормалью Nj к этой грани и нормалями ко всем другим граням этой же поверхности, — угол между нормалью Nj и нормалью Nl, то две грани pj и pl совместно являются образующими хотя бы одной вершины этой поверхности.

Чтобы найти третью грань — третье уравнение для нахождения точки в трехмерном пространстве, следует искать такую грань (например, p4 на рис. 6.5), между нормалью к которой и нормалями N1 и N2 углы также меньше тех углов, которые N1 и N2 образуют с нормалями несмежных граней.Такая грань будет смежной и p1, и p2.

Теорема. Пусть p — произвольная грань верхней (нижней) поверхности многогранника R допустимых решений задачи ЛП. Составим неубывающую последовательность углов между нормалью к этой грани и нормалями всех граней этой же поверхности (включая нормаль к этой же грани; этот угол равен нулю). Первые n минимальных отличных от нуля углов этой последовательности указывают на n граней, являющихся образующими некоторой вершины многогранника R.

Доказательство. Пусть среди выделенных таким образом граней есть грань, не являющаяся совместно с другими образующей одной вершины. Тогда, по теореме-гипотезе, существует образующая ту же вершину грань, не параллельная первой и такая, нормаль к которой составляет с нормалью к p угол, меньший, чем выделенный по указанной последовательности. Это противоречит правилу выбора n минимальных углов.

Особенности применения косинуса как функции меры угла

О величине угла в n-мерном пространстве мы можем судить только по его косинусу. Однако косинус не является монотонной функцией и в общем случае может служить мерой угла, если диапазон изменения этого угла не превышает .
Составим по (6.11) симметричную матрицу S, включенную в табл. 6.1
косинусов углов между всеми нормалями к граням верхней (нижней) поверхности выпуклого многогранника R.

Таблица 6.1. ГраньНормальN1 N2... Nr+n

p1	N1	1	cos(N1,N2)	...	cos(N1,Nr+n)
p2	N2	cos (N2,N1)	1	...	cos(N2,Nr+n)
...	...	...	...	...	...
pr	Nr	cos(Nr,N1)	cos(Nr,N2)	...	cos(Nr,Nr+n)
pr+1	Nr+1	cos(Nr+1,N1)	cos(Nr+1,N2)	...	cos(Nr+1,Nr+n)
...	...	...	...	...	...
pr+n	Nr+n	cos(Nr+n, N1)	cos(Nr+n,N2)	...	1

Выберем строку, соответствующую некоторой грани. Для комплектации граней, совместно с выбранной образующих общую вершину, выделим в этой строке n минимальных отличных от 0 и углов, то есть n максимальных косинусов, отличных от 1 и -1. Тем самым мы отдаем предпочтение вершинам с наиболее "пологими" склонами. При корректно сформулированной задаче такие грани "вокруг" некоторых вершин должны найтись. При этом углы между нормалями к граням, образующим общую вершину, не превышают . Следовательно, косинус может служить функцией меры углов в диапазоне их изменения.
Поясним выбор последовательности n косинусов.
Выбранная грань может быть параллельна некоторой другой грани или координатной плоскости, т.е. угол между их нормалями может быть равен либо нулю, либо . Очевидно, такие грани не могут быть образующими одной вершины.
На рис. 6.6 Qнижн={p1, p2, p3, p4}.

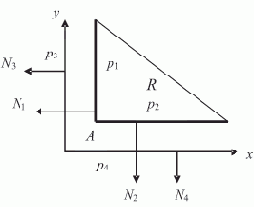
Рис. 6.6.  Пример, показывающий, когда грани не могут быть образующими одной вершины
Таблица косинусов углов имеет вид

Таблица 6.2. ГраньНормальN1 N2N3 N4

p1	N1	1	0	1	0
p2	N2	0	1	0	1
p3	N3	1	0	1	0
p4	N4	0	1		0

Из первой строки, допуская лишь одну единицу cos(N1,N1)=1), находим возможные образующие {p1, p2}. При этом поиск элементов последовательности ведем слева направо. Проверка подтверждает правильность выбора вершины A.
Аналогично, из второй строки находим {p2, p1}, что определяет ту же вершину. Третья строка определяет возможное множество образующих {p3, p2}, что не подтверждается проверкой. Четвертая строка также не определяет правильный выбор образующих {p4, p1}.

Обратим внимание на то, что все вышесказанные предположения и теоремы касаются граней, о которых доподлинно известно, что они входят в состав поверхности многогранника допустимых решений. Важным источником неприятностей являются координатные плоскости. Ведь мы не знаем, являются ли они действительными гранями, и вынуждены относить их к возможным. Отсюда и возможная ошибочность выводов.

На рис. 6.7 Qнижн={p1, p2, p3, p4, p5}.


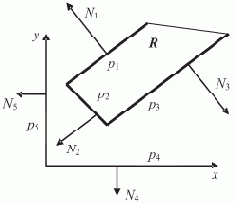
Рис. 6.7.  "Критические" случаи

Таблица косинусов углов имеет вид

Таблица 6.3. ГраньНормальN1 N2N3 N4 N5

p1	N1	1	0	-1	-v2/2	v2/2
p2	N2	0	1	0	v2/2	v2/2
p3	N3	-1	0	1	v2/2	-v2/2
p4	N4	-v2/2	v2/2	v2/2	1	0
p5	N5	v2/2	v2/2	-v2/2	0	1

Легко видеть, что анализ любой строки не позволит обнаружить вершину многогранника R.

Действительно, по первой строке формируется предполагаемое множество образующих {p1, p4}. Однако пересечение этих прямых не дает искомую вершину. И так — по всем строкам. Если бы было установлено, что ось y не входит в состав поверхности R, то соответствующий косинус можно бы было игнорировать, что привело бы к правильному выбору множества образующих {p1, p2}.

Анализ этого примера наводит на мысль: обязательно ли формировать верхнюю (нижнюю) поверхность до конца, присоединяя координатные плоскости? Ведь количество действительных граней, составляющих ее, достаточно для осуществления поиска вершины. А именно, если в выражении (6.7) r n, то на первом этапе поиска исключим из рассмотрения координатные плоскости. Это приведет к исключению из табл. 6.3

двух последних строк и столбцов. Легко видеть, что поиск вершины осуществляется успешно.

На рис. 6.8 демонстрируется случай, когда, несмотря на выполнение указанного выше неравенства, к поиску вершины необходимо подключать координатные плоскости.



Рис. 6.8.  Необходимость анализа координатных плоскостей

Три плоскости p1, p2, p3 совместно не являются образующими одной вершины. Только включение в рассмотрение плоскостей z = 0 или y = 0 позволяет найти вершины многогранника допустимых решений.

Грань может иметь нормаль, угол которой с нормалями некоторых "далеких" граней превышает . Например, углы между нормалями к координатным плоскостям составляют . Здесь использование косинуса может привести к неоднозначности при упорядочении углов.

Тогда воспользуемся следующим предположением:

На верхней (нижней) поверхности выпуклого многогранника R существует грань, нормаль к которой составляет с нормалями ко всем другим граням этой поверхности углы, не превышающие .

Это — предположение об обязательном существовании некоторых "срединных" граней, нормали к которым близки к середине диапазона изменения таких нормалей, — диапазона .

На рис. 6.9 отражена попытка представления некоторых крайних случаев, иллюстрирующих на плоскости существование "срединных" граней для разных выпуклых многогранников.


Рис. 6.9.  К существованию углов, не превышающих pi

Так, в многограннике R1 (треугольник) угол между нормалью N1

и другими нормалями не превышает . В прямоугольнике R2

максимальный угол, например, между нормалью N2 и другими нормалями, составляет . В многоугольнике R3, к примеру, нормаль N3

составляет со всеми нормалями угол, меньше .

Таким образом, мы предположили существование хотя бы одной грани, при анализе которой с помощью косинусов удается избежать искажений в определении того, в каком отношении находятся углы, которые нормаль к этой грани образует с нормалями к другим граням поверхности. Исключается случай, когда большему углу соответствует и больший косинус. Это приводит к необходимости одновременного параллельного анализа многих граней поверхности в качестве начальных, так как успех может быть достигнут не всегда.

Параллельное решение "плоской" задачи НП

Постановка задачи:
f(x,y) max
при ограничениях
g1(x,y) 0
... gm(x,y) 0
Могут быть условия x,y 0. Но они могут и отсутствовать, допуская поиск решения также в области отрицательных значений переменных.
Предположим:

Все ограничения разрешимы относительно всех переменных.

Ограничения и, возможно, условия неотрицательности решения образуют область R, ограниченную со всех сторон (рис. 6.2).

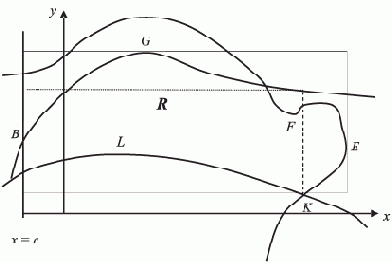
Рис. 6.2.  "Плоская" нелинейная задача оптимизации с нелинейными ограничениями

Предположим, как на рисунке, m = 4. (Одно ограничение, x-c 0, линейно.)
Решая попарно все равенства (границы R), полученные по ограничениям, и проверяя точки пересечения на удовлетворение остальным неравенствам-ограничениям, найдём все вершины, в нашем примере — {A, B, C, K}.
Координаты найденных вершин дают начальную информацию (прямоугольник показан пунктиром) о "минимальном" прямоугольнике D, включающем в себя область R. Однако некоторые кривые, ограничивающие R, сопряженные с двумя вершинами, могут, имея экстремум по некоторым координатам между ними, "выходить" из этого прямоугольника. Точки такого выхода надо найти, проверить на принадлежность R, если они существуют, и расширить D.
Для каждого i = 1, ... , m, разрешим gi
относительно x. Получим (возможно, неоднозначную) функцию
x = i (y).
Найдем множество экстремумов этой функции, решив уравнение
x' = '(y) = 0.
Для каждой точки экстремума проверяем, принадлежит ли она области R, т.е. выполняются ли для нее все ограничения. Такой точкой на рисунке является точка E.
Теперь то же самое надо проделать, разрешив все функции gi
относительно y,
y = ? i (x)
Найдем множество экстремумов этой функции, удовлетворяющих всем ограничениям. На рисунке это точки G, F, M, L.
Теперь мы нашли все точки, которые помогут нам очертить прямоугольник D, полностью вмещающий область R — область возможных решений задачи. Границы этого прямоугольника определяются минимальными и максимальными значениями координат всех найденных точек — точек пересечения кривых ограничений и точек экстремумов этих кривых, удовлетворяющих всем ограничениям задачи.
В нашем примере пусть A = (xA, yA), B = (xB, yB) и т.д. Тогда
xD1 = min{xA, xB, xG, xC, xF, xE, xM, xK, xL } = xA = xB,
xD2 = max{xA, xB, xG, xC, xF, xE, xM, xK, xL} = xE ,
yD1 = min{yA, yB, yG, yC, yF, yM, yE, yK, yL} = yK,
yD2 = max{yA, yB, yG, yC, yF, yM, yE, yK, yL} = yG.
Воспользуемся методом "сеток". Покроем область D сеткой с шагом ? x по x и ? y по y. Испытывая каждый узел на принадлежность R, и находя в нем значение f(x, y), выберем максимальное.
Допускается обобщение метода решения для произвольной размерности.

Параллельное решение задач НП при линейных ограничениях

Пусть решается задача
f(x1, ... ,xn) max
при ограничениях
g1(x1, ... ,xn) 0
g2(x1, ... ,xn) 0
...
gm(x1, ... ,xn) 0
и при условиях: gi — линейны, xi 0, i = 1, ... ,m.
Предположим, что гиперплоскости gi, i = 1, ... ,m, возможно, совместно с координатными плоскостями, образуют в n-мерном пространстве выпуклый многогранник R допустимых решений, т.е. область задания функции f.
Определим, как и ранее, все вершины {X1, ... ,Xn}, Xl
=(x1(l) , ... ,xn(l) ), l = 1, ... ,N, этого многогранника в результате решения Cm + nn систем n линейных уравнений на основе всех заданных и возможных его граней
Тогда множество точек X = (x1,x2, ... ,xn) этого многогранника описывается как , где 0 kl 1, . Или:

а целевая функция на многограннике R становится функцией параметров f(x1, ... ,x_n) = f*(k1, ... ,k_{N-1}).
Т.е., задавая разные значения k1, k2, ... ,k_{N-1} так, чтобы выполнялось условие 0 kl 1, так же как и для
мы можем организовать перебор всех точек R с некоторым шагом h по всем параметрам. Этим мы накладываем N-мерную "сетку" на многогранник R. В каждой точке-узле этой сетки мы будем находить значение функции f* и выберем максимальное. Шаг h должен быть выбран так, чтобы обеспечить необходимую точность решения задачи.
Распараллеливание возможно на двух этапах решения:

Распределение систем линейных уравнений между процессорами для нахождения всех вершин многогранника допустимых решений. (Эквивалентно прямому перебору при решении задачи линейного программирования.)

Распределение между процессорами узлов сетки — точек многогранника допустимых решений для нахождения и анализа в них значений целевой функции.

Метод допускает развитие и совершенствование.
Например, движение в сторону возрастания функции f может быть направленным, определяемым с помощью конечно-разностных значений частных производных по параметрам kl в точке текущего анализа
функции f. Это вариант так называемого градиентного метода. Эти же значения частных производных могут определять переменный шаг h.

Пример (рис. 6.1)

f(x,y)=x2+y max

при ограничениях

-x-2y+12 0

-3x-y+21 0

и при условии x,y 0.


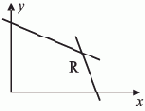
Рис. 6.1.  Нелинейная задача с линейными ограничениями

Решая попарно уравнения границ, находим

Xl=(0,0), X2=(0,6), X3=(6,3), X4=(7,0).

Уравнение многогранника R:

Пусть h — шаг изменения каждого ki для получения испытываемой точки X многогранника R. Будем перебирать точки

k1 = 0, k2 = 0, k3 = 0 (тем самым k4 = 1);

k1 = h, k2 = 0, k3 = 0 (k4 = 1-h);

k1 = h, k2 = h, k3 = 0 (k4 = 1-2h);

k1 = h, k2 = h, k3 = h (k4 = 1-3h);

k1 = 2h, k2 = h, k3 = h (k4 = 1-4h);

...

Однако нам надо следить, чтобы величина k4 = 1 - k1 - k2 - k3

оставалась неотрицательной.

Выполнив такой перебор, например, для h = 0,1, получим max f(x,y) = f*(k1 = 0, k2 = 0, k3 = 0, k4 = 1) = f(7,0) = 49.

Предпосылки метода

Ниже предлагается метод нахождения вершины многогранника допустимых решений задачи линейного программирования для начала процесса параллельного поиска оптимального решения. В основе метода лежит предположение, что для некоторых вершин образующие их грани имеют нормали, которые составляют с каждой из этих нормалей минимальные углы. При обобщении на произвольное пространство обсуждается возможность использования косинусов углов между нормалями в качестве функции меры.
Параллельный алгоритм решения задачи линейного программирования (ЛП) ориентирован на применение SPMD-технологии ("одна программа — много потоков данных"), наиболее эффективной при организации распределенных (в локальной вычислительной сети) и параллельных (в многопроцессорной вычислительной системе) вычислений. Метод базируется на отказе от традиционного ввода свободных переменных. Поиск решения производится непосредственно в n-мерном пространстве, что сохраняет наглядность "физического смысла" задачи.
Суть метода в следующем. Первоначально должна быть известна некоторая вершина многогранника допустимых решений вместе с системой уравнений границ на основе ограничений и возможных границ — координатных плоскостей, которым эта вершина удовлетворяет. Эта вершина определяет начальный или опорный план. Далее с помощью множества процессоров вычислительной системы или рабочих станций вычислительной сети производится одновременное и независимое смещение вдоль ребер, исходящих из вершины, для поиска одной или более вершин с "лучшим" (большим или меньшим, в зависимости от поставленной задачи) значением целевой функции. Процессоры переключаются на новую вершину, и процесс продолжается до решения задачи.
Нетрадиционность этого подхода обусловлена высокой размерностью задачи и необходимостью распараллеливания. Распараллеливание требует, в свою очередь, пересмотра алгоритмов, ранее ориентированных только на сокращение количества операций и не обеспечивающих эффективную, одновременную загрузку оборудования, тем более — локальной вычислительной сети.
В лекции 4 курса "Архитектура параллельных вычислительных систем" даются рекомендации по параллельному нахождению опорного плана на основе прямого перебора. На задачах малой размерности, рассматриваемых в качестве примеров, это вполне допустимо, однако практическая задача размерности n = 36 и с числом ограничений m = 18 привела к недопустимому времени счета. Компьютеры стали бы искать опорный план не один месяц, что связано с экспоненциальной сложностью такого перебора.
Таким образом, необходимо найти "быстрый" параллельный алгоритм нахождения опорного плана.
Здесь можно было бы воспользоваться одним из известных "традиционных" методов. Однако желание максимально использовать "физический смысл" задачи и потому остаться в n-мерном пространстве сулит выявление замечательных свойств выпуклого многогранника допустимых решений, которые скрыты при традиционном абстрагировании.

Принцип внешней точки

Итак, поставлена задача ЛП
Z = c1x1 + c2x2 + ... + cnxn max
при ограничениях
q1 = a11x1 + ... + a1nxn b1 (6.1)
... qm = am1x1 + ... + amnxn bm
и при условии
x1 0, ... ,xn 0.
Если в ограничениях заменить знак "" на "=", получим множество действительных (т.е. действительно являющихся) границ выпуклого многогранника R допустимых решений. Однако в общем случае часть его границ определяется условиями, также записанными в виде равенств. Это — возможные границы многогранника.
Таким образом, грани многогранника R формируются на основе множества m действительных и n возможных границ:
q1 & = a11x1 + ... + a1n xn - b1 = 0
...
qm = am1x1 + ... + amnxn - bm = 0 (6.2)
qm+1 = x1 = 0
...
qm+n = xn = 0.
Здесь обозначение qi используется для названия соответствующих плоскостей и ограничений.
Тогда принципиально возможен выбор комбинаций по n уравнений из (6.2) и их совместное решение. Если решение существует, оно не отрицательно и удовлетворяет всем не использованным при этом ограничениям (6.1), то это решение определяет координаты одной из вершин многогранника R. Однако, как говорилось выше, нет гарантированных оценок времени получения первой вершины, а полный перебор Cnm + n систем n уравнений обладает экспоненциальной сложностью.
Локализуем поиск вершины многогранника R, освободившись от некоторых "лишних" уравнений из (6.2).
Установим направление роста целевой функции, записав ее дифференциал:
dZ = c1dx1 + c2dx2 + ... + cndxn.
Сообщив одинаковое положительное приращение dx всем переменным, получим
dZ = (c1 + c2 + ... + cn )dx.
Следовательно, сумма коэффициентов целевой функции (в отличие от более точной оценки с помощью градиента) определяет направление ее роста: если

(6.3)

Z растет, удаляясь от начала координат, если

(6.4)

Z растет, приближаясь к началу координат.
Случай может быть причислен как к (6.3), так и к (6.4).
Выберем точку начала координат O (0, 0, ... , 0). Если все ограничения (6.1) в ней выполняются, эта точка является вершиной многогранника R, и наш поиск хотя бы одной вершины может быть успешно закончен.
В противном случае будем считать эту точку внешней точкой, удобной для рассмотрения многогранника R "со стороны".

А именно, выделим множество тех плоскостей в (6.2), которые являются действительными гранями многогранника R и для которых в точке O выполняются ограничения задачи (6.1). Дополним это множество плоскостей n координатными плоскостями. Назовем образованную поверхность верхней поверхностью Qверхн

выпуклого многогранника R допустимых решений задачи ЛП. Координатные плоскости включаются в рассмотрение, для того чтобы можно было исследовать вершины R, принадлежащие этим плоскостям.

Аналогично, остальные плоскости (грани), для которых в точке O не выполняются ограничения (6.1), дополненные координатными плоскостями, образуют нижнюю поверхность Qнижн многогранника R.

Очевидно, если сумма коэффициентов целевой функции положительна, то есть Z растет, удаляясь от точки O, то решение задачи ЛП следует искать среди вершин многогранника R на его верхней поверхности. В противном случае — на нижней поверхности.

Проследим на приведенном в лекции 4 курса "Архитектура параллельных вычислительных систем" примере рассматриваемые здесь построения. Для этого повторим постановку и дополним графическую интерпретацию представленной там задачи.

Задача формулировалась следующим образом:

Z = 26x + 20y + 21z max

при ограничениях

q1 = 2x + 7y - 76z + 222 0

q2 = -8x + 9y - 8z + 64 0

q3 = -8x + 13y - 24z +96 0 (6.5)

q4 = -x - 6y - z + 70 0

q5 = -2x - 7y - 2z + 90 0

q6 = 33x + 3y + 22z - 165 0

и при условии неотрицательности переменных, о чем в дальнейшем можно не упоминать.

Так как сумма коэффициентов целевой функции положительна, то нас будет интересовать верхняя поверхность многогранника R допустимых решений. При x = y = z = 0 справедливы неравенства для q1

,... , q5. Следовательно,

Qверхн = {q1, q2, q3, q4, q5, q7, q8, q9}. (6.6)

На рис. 6.3 3 ребра верхней поверхности выделены. Координаты точек выбраны при построении примера и приведены для контроля. Считаем их неизвестными; их необходимо получить.


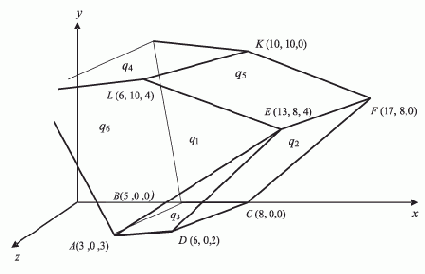
Рис. 6.3.  Многогранник допустимых решений с выделенными рёбрами

В данном случае мы получили малый выигрыш, исключив из рассмотрения единственную грань с образуемыми ею вершинами. Однако в произвольном случае форма R может быть разнообразной, и подобное сокращение рассматриваемых ограничений, то есть связанных с ними граней, может быть существенным. Да и сейчас мы видим, что число вершин, среди которых необходим поиск, весьма сократилось — до шести отмеченных на рисунке.

Развитие стратегии решения задачи ЛП

Выделяя на многограннике R допустимых решений верхнюю и нижнюю поверхности, мы на деле не столько стремимся "подобраться" поближе к вершине-решению, сколько стремимся расчленить задачу, локализовать поиск опорного плана. Если мы с помощью указанных косинусов начнем исследовать совместно всю совокупность граней многогранника, то окажемся во власти неразрешимых коллизий. Ни о каком упорядочении углов в этом случае не может быть речи, так как во всем диапазоне [0, 2] изменения углов между нормалями к граням косинус никогда не даст однозначного ответа об отношении между этими углами.

Многогранник R может иметь столь причудливую форму, что знание значения целевой функции в некоторой его вершине нисколько не определяет того, за сколько шагов будет найдена вершина-решение. Например, двигаясь из вершины, в которой значение целевой функции меньше, можно за один шаг второго этапа алгоритма достичь, как смежную, вершину-решение. В то же время, стремясь найти вершину с большим значением целевой функции, можно оказаться в ситуации, когда для достижения вершины-решения потребуется несколько шагов. Это говорит о том, что анализ суммы коэффициентов целевой функции для выбора верхней или нижней поверхности многогранника R не столь важен.

Более того, выбранная таким образом поверхность не всегда может привести к успеху.
Например, на рис. 6.6 верхнюю поверхность образуют грань (ребро), противоположная вершине A, и, возможно, координатные плоскости (оси).
Поскольку при анализе этой поверхности другие грани исключены из рассмотрения, то нет системы двух уравнений, результатом решения которой стали бы вершины, образуемые этой гранью. Мы зашли бы в тупик, если бы не позволили себе рассмотреть и другую, нижнюю, поверхность.
Кстати, в нашем примере нижняя поверхность определяется следующим образом:
Qнижн = {q6, q7, q8, q9}.
Составим для нее матрицу S косинусов в составе табл. 6.5.

Таблица 6.5. ГраньНормаль N6 N7 N8 N9

q6	N6	1	0,83	0,23	0,56
q7	N7	0,83	1	0	0
q8	N8	0,23	0	1	0
q9	N9	0,56	0	0	1

В результате анализа первой строки, соответствующей грани q6, находим грани {q6, q7, q9}, возможно, образующие некоторую вершину. В результате решения выделенной системы уравнений получаем точку (0, 55, 0). Эта точка не удовлетворяет ограничениям q4 0 и q5 0. Мы видим по рисунку 6.3, что ошибки бы не произошло, если бы из рассмотрения не была исключена грань q4. Мы делаем вывод о том, что "на стыке" поверхностей, где частично отсутствует информация об образующих некоторых вершин многогранника R, возможны ошибки. Нормаль к q4 составила бы с нормалью к q6 меньший угол, который был бы включен в формируемую комбинацию трех углов.

В результате анализа строки, соответствующей грани q7

(игнорируя нули), находим только грани q6 и q7. Однако для нахождения третьей грани придется все же организовать перебор (именно перебор) нулей. Проверим комбинацию граней {q6, q7, q8}. Их совместное решение определяет точку (0, 75, 0), не удовлетворяющую тем же ограничениям. Комбинация {q6, q7, q9} уже рассматривалась.

Анализ следующей строки приводит к необходимости проверки комбинаций {q6, q7, q8} и {q6, q8, q9}. Первая комбинация уже исследовалась, а вторая приводит к получению точки (5, 0, 0), удовлетворяющей всем ограничениям (точка B на рис. 6.3).

Анализ последней строки приводит к необходимости проверки комбинаций {q6, q7, q9} и {q6, q8, q9}. Обе комбинации уже рассматривались: первая — как неудачная, вторая — повторно образующая вершину.

Легко видеть, что если бы мы не выполняли перебор комбинаций нулей, то так и не получили бы вершину, так как при первой возможной комбинации, обусловленной алгоритмом, она ни разу не обнаружилась.

Отсюда вывод: в общем случае необходимо избегать анализа строк матрицы S, соответствующих координатным плоскостям. Помимо того, что это — лишь возможные, но не действительные грани, углы, образуемые нормалями к ним и нормалями к другим граням, могут превышать . Это с большой вероятностью приводит к ошибкам в определении соотношения углов.


Так, в рассмотренном примере анализа верхней поверхности многогранника R достаточно было исследовать первые пять строк матрицы S ( табл. 6.1), опираясь на предположение о наличии "срединных" граней. Ведь в результате этого анализа вершины были найдены.

Напомним, что, выделяя верхнюю и нижнюю поверхности, мы некоторые вершины делаем недоступными для предлагаемого метода. Это — вершины "на стыке" поверхностей. В данном случае это, например, вершины, образуемые комбинациями {q1, q6, q8}, {q4, q6, q9} и др.

Рассмотренный пример анализа нижней поверхности многогранника R приводит к уточнению алгоритма нахождения опорного плана.

Нули — косинусы углов между осями координат — не всегда удается игнорировать. Это характерно для того случая, когда действительных граней, образующих рассматриваемую поверхность, недостаточно (r < n) или анализ соответствующих им строк матрицы S не приводит к успеху. Тогда приходится анализировать строки, соответствующие координатным плоскостям, "добирая" нулевые значения косинусов до общего количества n таких косинусов. При этом неизбежен перебор всех возможных комбинаций таких нулей.

Можно было бы сделать здесь вывод о том, что при подозрении о таких трудностях немедленно следует приступить к поиску опорного плана на другой поверхности. Однако мы не доказали, что хотя бы одна вершина обязательно будет найдена. Это приводит к необходимой готовности воспользоваться, в случае неудачи, одним из проверенных, традиционных методов нахождения опорного плана решения задачи ЛП, — более сложного и практически не распараллеливаемого.

Параллельное программирование

Граф-схемы параллельных алгоритмов

Представим себе программу решения задачи, которая отображает последовательное изложение алгоритма на машинном языке, ассемблере или ЯВУ. Предположим, что, анализируя эту программу, нам удалось разбить её на отдельные модули и выделить для каждого из них множества входных и выходных данных так, чтобы установить взаимодействие модулей по информации.
Например, программа F представляется как
F = F1(X1 , X2 ; X3 , X4 ) F2 (X2 ; X5 ) F3 (X3 ; X6 ) F4 (X1 , X4 ; X7 ) F5 (X3 , X4 , X5 ; X8 ) F6 (X3 , X4 , X7 ; X9 ) F7 (X5 , X7 ; X10) F8 (X6 , X8 , X9 , X10 ; Y), где точкой с запятой отделены входные данные от выходных, X = {X1, X2} — исходные данные задачи, Y — выходные данные или результат.
Итак, мы разбили заданный алгоритм решения задачи на ряд модулей, операторов, работ и установили информационную взаимосвязь этих работ. Чтобы подчеркнуть общность задач и методов распараллеливания, не ограничивающуюся применением только для ВС, будем пользоваться термином работа.
Для решения задач оптимального выполнения работ многими исполнителями (т.е. процессорами ВС) нам понадобятся временные оценки выполнения как программы в целом, так и каждого выделенного модуля, т.е. каждой работы. Эти оценки могут быть выполнены как экспериментально, так и на основе количества операций и производительности процессоров, предполагаемых к использованию.
Пусть относительно данного алгоритма и предполагаемой ВС нам известны следующие оценки T = {t1, t2, ... , t8}.
Тогда, чтобы отразить прохождение обрабатываемой информации и выявить возможности распараллеливания, представим информационную граф-схему алгоритма или информационный граф G (рис. 7.1). Вершины соответствуют работам. Дуги отражают частичную упорядоченность работ.

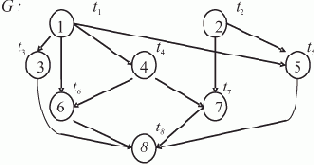
Рис. 7.1.  Информационный граф алгоритма
А именно, если работа ? использует в качестве входной информации результат выполнения работы , то её выполнение не может быть начато до того, как закончится выполнение работы . Такая преемственность информации и отражена в графе.
Граф G — взвешенный, ориентированный и не содержит контуров. (Т.к. время выполнения алгоритма конечно, то программные циклы либо погружены внутрь работ, либо развёрнуты.)

Например, представим себе информационный граф, соответствующий скалярному умножению векторов заданной длины: A = B ? C способом "пирамиды", В = {b1 , ... , b8}, C = {c1 , ... , c8}. Схема счёта показана на рис. 7.2.


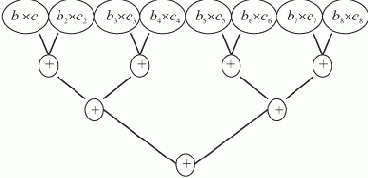
Рис. 7.2.  Схема счёта "пирамидой"

Примем время сложения равным единице. Время умножения пусть превышает время сложения в четыре раза. Информационный граф G, соответствующий счёту способом "пирамиды", представлен на рис. 7.3.


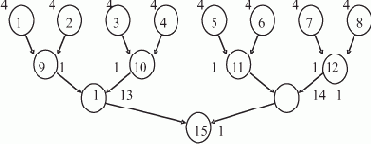
Рис. 7.3.  Информационный граф — "пирамида"

Мы рассмотрели составление информационных графов. Можно рассматривать информационно-логические графы, если учитывать альтернативные ветви алгоритмов.

Например, может быть целесообразным следующее разбиение программы (алгоритма) на модули (работы):

F = F1(X1; X2) if A then F2(X2; X3) else F3(X1;X4) F4(X1, X3, X4; Y).

Информационно-логический граф G — на рис. 7.4.


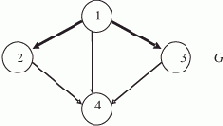
Рис. 7.4.  Информационно-логический граф

Преемственность информации (1 2), а также (1 3), при наличии "жирной" стрелки "по управлению" можно не указывать, так как частичная упорядоченность работ в таком случае полностью определена.

Рассмотрение информационно-логических графов сильно усложняет решение задач оптимизации параллельных вычислений. Практически ограничиваются планированием выполнения самой сложной, трудоемкой ветви алгоритма или решают её для разных ветвей отдельно, — т.е. сводят оптимизацию к рассмотрению только информационных графов.

Для формальных исследований информационный граф G представляется матрицей следования S, или, с добавлением столбцов весов, — расширенной матрицей следования S*. При этом, т.к. граф G не содержит контуров (циклов), то S может быть сведена к треугольной "правильным" выбором нумерации вершин. Ниже (рис. 7.5) приведены матрицы S и S* для графа, представленного на рис. 7.1, и для некоторых известных значений весов.



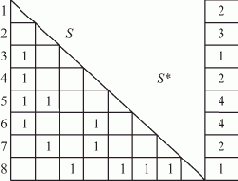
Рис. 7.5.  Матрица следования с задающими связями

Определение 1. Назовём все связи по информации, обусловленные исходным видом графа G, задающими связями.

Определение 2.

Путями в графе G будем называть последовательности вершин вида a1, a2 , ... , as такие, что для любой пары соседних вершин ai и ai+1 существует дуга, исходящая из вершины ai и входящая в вершину ai+1.

Будем считать все пути в графе G допустимыми, т.е. реально существующими ветвями отображаемой программы.

Определение 3. Длиной пути в информационном графе G назовём сумму весов вершин, составляющих этот путь.

Определение 4. Путь максимальной длины Tкр в информационном графе G назовём критическим.

В одном графе может быть несколько путей равной длины, являющихся критическими.

Если в графе G есть дуга, исходящая из вершины a и входящая в вершину b, т.е. существует задающая связь a b, а также есть дуга, исходящая из вершины b и входящая в вершину c, т.е. существует задающая связь b c, но нет задающей связи a c, очевидно, что последовательный порядок выполнения работ a и c определяется двумя указанными задающими связями. Т.е. граф G можно дополнить дугой, соответствующей связи a c, что только подтвердит заданную частичную упорядоченность работ.

Определение 5. Множество связей, которые введены направленно внутри всех пар работ, принадлежащих одному пути в графе G и не связанных задающими связями, назовём множеством транзитивных связей.

Транзитивные связи полностью определяются задающими связями.

Алгоритм 1 дополнения треугольной матрицы S транзитивными связями.

Организуем просмотр сверху вниз строк матрицы следования S.

В очередной i-й строке организуем просмотр элементов в порядке увеличения j номеров столбцов.

Если (i, j)=1, складываем строки i и j по операции дизъюнкции.

Если исходная матрица следования S нетреугольная, последовательный просмотр её строк производится неоднократно до установления факта неизменности окончательно полученной матрицы.)

Конец алгоритма.


В представленном выше примере после введения всех транзитивных связей матрица следования S примет вид, представленный на рисунке 7.6)рисунке 7.6 (введённые транзитивные связи выделены курсивом).


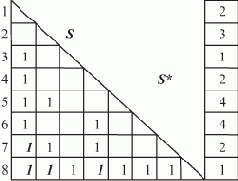
Рис. 7.6.  Матрица следования с транзитивными связями

С помощью введения транзитивных связей в нетреугольной матрице следования устанавливается наличие контуров в графе G. О наличии контуров свидетельствуют появившиеся ненулевые диагональные элементы, указывающие на связь вида a a.

Например, пусть задан граф G на рис. 7.7.


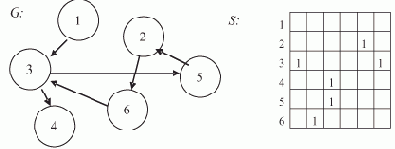
Рис. 7.7.  Граф алгоритма и матрица следования

После первого шага преобразования S принимает вид, показанный на рис. 7.8.


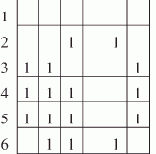
Рис. 7.8.  Первый шаг обнаружения контура

После второго шага преобразования S принимает вид, показанный на рис. 7.9.


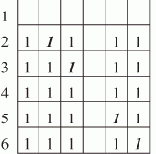
Рис. 7.9.  Обнаружение контура

Т.к. на главной диагонали матрицы появились единицы, то граф G содержит циклы (контуры). Из рисунка графа виден цикл 2 6 3 5 . "Участники" цикла отмечены единицами на главной диагонали.

Определение 6. Работы a и b будем называть взаимно независимыми, если в матрице следования S выполняется условие (a, b) = (b, a) = 0.

Определение 7. Работы {ai}, i = 1, ... , s, образуют полное множество взаимно независимых работ (ПМВНР), если для любой работы j {ai} существует задающая или транзитивная связь (a? , j) = 1 или {(j , a?) =1} (?,? {1 , ... , s}).

Например, для графа G, представленного на рис. 7.1, после введения транзитивных связей, что учтено в матрице следования на рис. 7.6, можно установить следующие ПМВНР: {1,2}, {2,3,4}, {3,4,5}, {2,3,6}, {3,5,6,7}, {8}.

Неформальная постановка задач параллельного программирования ВС

Высокая производительность ВС достигается структурными методами, основанными на параллельной обработке информации. ВС содержит несколько процессоров или операционных устройств, способных одновременно, но с необходимой синхронизацией, выполнять доли возлагаемых на них работ по реализации алгоритма решения задачи.
Проблема её программирования — это проблема планирования распараллеливания. Это требует разбиения алгоритма на, в общем случае, частично упорядоченное множество работ, назначения этих работ на процессоры с учетом синхронизации их выполнения в соответствии с обязательным порядком следования.
С ориентацией на достижение максимальной производительности ВС, а также на специальное применение в составе конкретных систем, например, в составе сложных систем управления, различают две взаимно-обратные задачи параллельного программирования.
Задача 1. Для заданного комплекса информационно и по управлению взаимосвязанных задач (частично упорядоченного множества задач), для заданной архитектуры ВС (наличие многих процессоров в однородной ВС, наличие процессоров разной специализации или производительности в неоднородной ВС, наличие или отсутствие ООП и т.д.), а также для заданного ограничения на допустимое время вычислительного процесса, выбрать комплектацию ВС минимальной стоимости.
Под стоимостью понимают вес каждого типа процессоров, который необходимо учитывать при выборе оптимальной комплектации. В частности, это стоимость разработки или цена одного процессора.
В однородной ВС задача 1 вырождается в задачу нахождения минимального числа процессоров, необходимого для решения данного комплекса взаимосвязанных задач за время, не превышающее заданное.
Задача 2. Найти план решения за минимальное время данного комплекса информационно и по управлению взаимосвязанных задач на данной ВС.

Нижняя оценка минимального числа

Алгоритм 5.

Первоначально полагаем n = 0.

Организуем перебор всех отрезков [?1, ?2]
[0, T] в порядке
Всего таких отрезков T(T+1)/2.

Для очередного анализируемого отрезка времени [?1, ?2] находим значение

Если n' > n, выполняем операцию n := n'. После перебора всех отрезков окажется найденным значение n, которое равно максимальному из значений, удовлетворяющих (7.2).

Пример. Нахождение оценки n.
Нахождение (4)(?1,?2) будем иллюстрировать графически, возможными временными диаграммами (рис. 7.19).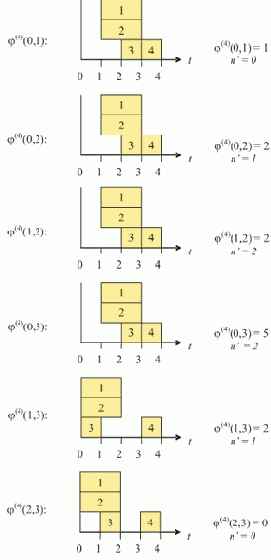

увеличить изображение
Рис. 7.19.  Нахождение нижней оценки числа исполнителей

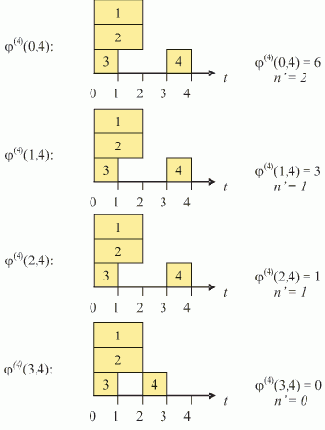
Рис. 7.19.  Окончание

В результате анализа всех отрезков находим n = max n' = 2.

Нижняя оценка минимального времени выполнения данного алгоритма на ВС

Алгоритм 6.

Первоначально полагаем

Организуем перебор всех отрезков [?1, ?2]
[0, T] в той же последовательности, что и в предыдущем алгоритме. (В процессе выполнения данного алгоритма значение T может увеличиваться, что при данном порядке перебора не приведёт к усложнению алгоритма.)

Для очередного анализируемого отрезка времени [?1, ?2] находим значение
d = (T)(?1,?2) - n(?2 - ?1)

Если d > 0, выполняем операцию T := T + ] d/n [.

Полагаем ?2j(T) := ?2j(T) + ] d/n [ , j = 1 , ... , m.

После перебора всех отрезков [?1, ?2] окажется найденным окончательное значение T — нижняя оценка минимального времени выполнения данного алгоритма на данной ВС.
Пример.
Произведём оценку T для графа G, рассмотренного в предыдущем примере, и ВС, состоящей из двух процессоров, n = 2 (рис. 7.20).

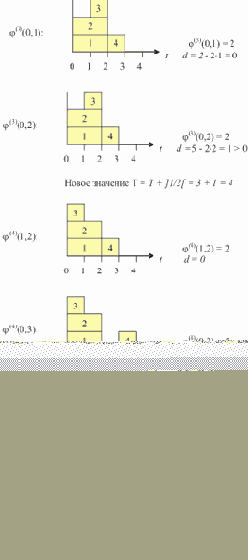
увеличить изображение
Рис. 7.20.  Оценка снизу минимального времени выполнения работ

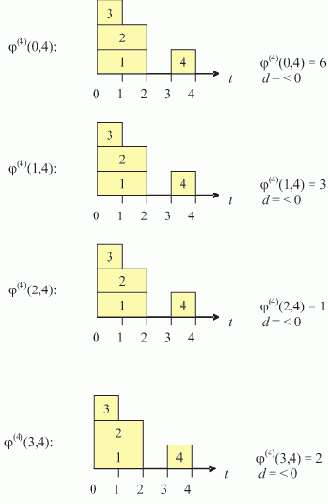
Рис. 7.20.  Окончание
Первоначально находим
После перебора всех отрезков, с учётом уточнения оценки времени в процессе этого перебора, окончательно находим T = 4.

Решение задачи 1 распараллеливания для однородных ВС

Формулировка задачи: Для данного алгоритма, которому соответствует информационный граф G, и для времени T, отведённого для его выполнения, найти наименьшее число n процессоров, составляющих однородную ВС, и план выполнения работ на них.
Метод точного решения задачи (метод "ветвей и границ") основан на следующей основной теореме.
Теорема. Для того чтобы значение n являлось наименьшим числом процессоров однородной ВС, которая выполняет алгоритм, представленный информационным графом G = (X, P, Г ), за время, не превышающее заданное значение T, необходимо и достаточно, чтобы n было наименьшим числом, для которого можно построить граф G' = (X, P, Г'), объединив вершины, соответствующие работам каждого ПМВНР, который содержит r > n работ r - n ориентированными дугами в n путей не содержащих общих вершин. При этом длина критического пути в графе G' не должна превышать значение T.
Алгоритм 7 решения задачи 1 — нахождения графа-решения G'

Для графа G и времени T находим значения ранних {?1j} и поздних {?j(T)}, j = 1 , ... , m, сроков окончания выполнения работ. (Если задача поставлена корректно, то

Находим оценку минимального числа n процессоров, которое необходимо для выполнения заданного алгоритма за время, не превышающее T.

Пусть ? — номер шага решения задачи. Полагаем ? = 1.

Находим наименьшее значение t? такое, что
F(?11, ?12 , ... , ?1m, t? ) = r? > n.
Если такого t? нет, то n — решение задачи.

Выделяем множество работ A? = {j?}, ? =1 , ... , r?, для которых
?1j? - tj? t? < ?1?,
т.е. тех работ, которые "порождают" данное значение F. Множество A является подмножеством некоторого ПМВНР.

Предположим, что мы можем упорядочивать комбинации дополнительных связей внутри множества A?. Введём очередную комбинацию r - n связей, как указано в теореме — так, чтобы длина критического пути в изменившемся при этом графе G не превысила T.

Если такая комбинация найдена, выполняем операцию ? := ? + 1, уточняем значения {?1j} и {?2j(T)} с учётом введённых связей, переходим к выполнению 4.

Если такой комбинации связей не существует, либо все они уже испытаны, выполняем операцию ? := ? - 1.

Если ? = 0, т.е.
на первом же шаге сглаживание загрузки процессоров не приводит к подтверждению того, что n — решение, выполняем операцию n := n + 1 и переходим к выполнению 3. Если ? 0, восстанавливаем значения {?1j} и {?2j(T)} , найденные на данном шаге, и переходим к выполнению 6.

Конец алгоритма.
Таким образом, суть алгоритма в том, что, реализуя общий подход, который называется метод "ветвей и границ", мы, выбрав начальное расписание, где все работы занимают на оси времени крайнее левое положение, продвигаемся шаг за шагом и находим точки на оси времени, в которых функция плотности загрузки превышает первоначально испытываемое n. Пытаемся сгладить значение этой функции, введя дополнительные связи между работами, допускаемые ограничением T. В случае неудачи вернёмся на шаг назад и попытаемся ввести другую комбинацию связей. При переборе всех комбинаций связей на первом шаге, не приведших к успеху, увеличим предполагаемое число процессоров и начнём процесс сглаживания функции плотности загрузки сначала.
Примечания

Как упорядочить вводимые комбинации связей?
Пусть A? — множество взаимно независимых работ, между которыми нужно ввести r - n связей по условию теоремы, т.е. построить некоторый граф, связывающий вершины A?. Построим матрицу следования L?, соответствующую этому графу. Первоначально эта матрица — нулевая. Вводим r? - n единиц так, чтобы:

граф, соответствующий получаемой при этом матрице, не содержал контуров (отсюда, в частности, следует, что диагональные элементы всегда должны быть нулевыми);

в каждой строке и в каждом столбце матрицы не должно содержаться больше одной единицы (следует из Теоремы о возможных путях, не содержащих общих работ).

Перемещая последнюю единицу сначала по строке, затем по столбцам, затем перейдя к предпоследней единице и т.д., осуществляем перебор всех возможных комбинаций связей между работами множества A?.

Можно рекомендовать следующий способ сокращения перебора: введение дополнительных связей в пункте 6 алгоритма производить не только по критерию допустимого увеличения длины критического пути, но и по значениям функции минимальной загрузки отрезка.


А именно, вводя очередную комбинацию связей на ?-м шаге сглаживания функции плотности загрузки, не приводящую к увеличению длины критического пути сверх заданного T, необходимо вновь пересчитать значение функции с учётом новых связей на всех отрезках [?1, ?2] [t?, T] . Если для испытываемого значения n на этих отрезках выполняется соотношение (7.2), данная комбинация связей может быть признана удачной. Таким образом, выполнение соотношения (7.2) в совокупности с допустимым увеличением длины критического пути определяет "границы" при ветвлении.

(Напомним, что метод "ветвей и границ", как метод перебора, обладает экспоненциальной сложностью, является NP-трудным. Поэтому сокращение перебора — очень важная задача.)
Пример.
Найдём минимальное число n процессоров, необходимое для выполнения алгоритма, который представлен графом G на рисунке 7.21а, за время T = 7.

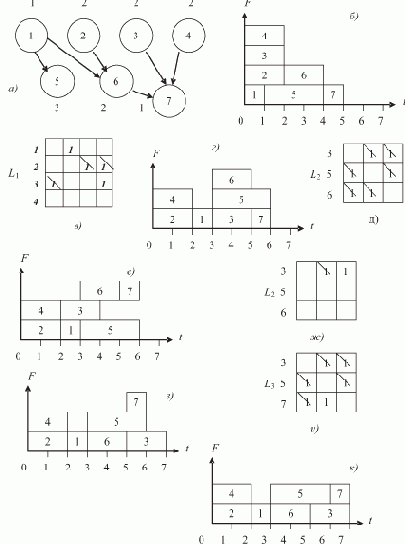
Рис. 7.21.  Последовательные действия при точном решении задачи 1
По алгоритму 4 найдёем нижнюю оценку n = 2, исследовав 28 значений (7)(?1,?2) для всех [?1, ?2] [0, 7] . При этом ?11 = 1, ?12 = ?13
= ?14 = 2, ?15 = ?16 = 4, ?17 = 5, ?21(7) = ?22(7) = 4, ?23 (7) = ?24(7) = ?26 (7) = 6, ?25(7) = ?27 = 7. Мы не собираемся впредь иллюстрировать нахождение функции минимальной загрузки, поэтому не будем приводить динамически уточняемые значения поздних сроков окончания выполнения работ.
F(?11 , ... , ?17) = 4 > 2, т.е. t1 = 0. В формировании этого значения участвуют работы 1, 2, 3, 4. Составим квадратную матрицу L1 (рис. 7.21в) с первоначально нулевыми элементами. Постараемся последовательно ввести в неё два единичных элемента. Первая возможная комбинация двух таких элементов соответствует связям 3 2 1. Длина критического пути в графе G, дополненном дугами в соответствии с этими связями, превышает 7. Пробуем заменить вторую связь следующей возможной. Новая испытываемая комбинация связей 4 2
1 также приводит к недопустимому увеличению длины критического пути. Единичные элементы, соответствующие отвергнутым связям, на рисунке зачёркнуты.


Вновь меняем вторую связь, полагая равным единице первый элемент третьей строки матрицы L1. Новая комбинация связей 2 1 3 не приводит к недопустимому увеличению длины критического пути в графе G. По графу, учитывающему введённые связи, находим ранние и поздние сроки окончания выполнения работ. На рис. 7.21г, приведена диаграмма выполнения алгоритма при ранних сроках {?11 = 3, ?12 = ?14 = 2}, ?13 = ?16 = 5, ?15 = ?17 = 6 окончания выполнения работ. Связи между работами не указаны.
Найдём t2 = 3 такое, что F(3, 2, 5, 2, 6, 5, 6, 3) = 3 > 2. Данное значение функции плотности загрузки определяется выполнением работ 3, 5, 6. Составляем матрицу L2 (рис. 7.21д) и стараемся ввести в ней единственный единичный элемент. Однако перебор всех возможных способов введения такого элемента приводит к длине критического пути в образующемся графе, превышающей 7. Возвращаемся на шаг назад к анализу матрицы L1 и пробуем ввести другую допустимую комбинацию связей. Такой комбинацией является 2 1, 4 3. На рис. 7.21е
представлена диаграмма выполнения алгоритма при уточнённых ранних сроках окончания выполнения работ ?11 = 3, ?12 = ?14 = 2 ?13 = 4, ?15 = ?17 = 6, ?16 = 5
Вновь находим значение t2 = 3 такое, что F(3, 2, 4, 2, 6, 5, 6, 3) = 3 > 2. (Совпадение значений t2 и выделенных работ с ранее исследованными является скорее случайным.) Вновь формируем матрицу L2 (индекс указывает номер шага, новая матрица L2 в общем случае ничем не схожа с аналогичной ранее рассмотренной матрицей), и находим первую из допустимых связей — связь 6
3 (рис. 7.21ж).
Вновь (рис. 7.21з) находим значение t3 = 5, где плотность загрузки превышает значение 2. Составляем матрицу L3 (рис. 7.21и). Находим в ней единственную единицу, соответствующую допустимой связи 5 7. На рис. 7.21к представлена диаграмма выполнения алгоритма, удовлетворяющая решению задачи.
Собственно расписание определяется найденными на последнем шаге значениями {?1j} .

Решение задачи 2 распараллеливания для однородных ВС

Формулировка задачи: Для данного алгоритма, которому соответствует информационный граф G, найти минимальное время T и план выполнения этого алгоритма на данной однородной ВС, содержащей n процессоров.
Теорема. Для того, чтобы T было минимальным временем выполнения алгоритма, представленного информационным графом G = (X, P, Г), на однородной ВС, состоящей из n процессоров, необходимо и достаточно, чтобы T было наименьшей из возможных длин критических путей в графах вида G'= (X, P, Г'), что получены из данного объединением вершин, соответствующих работам каждого ПМВНР, который содержит r > n работ, r - n ориентированными дугами в n путей, не содержащих общих вершин.

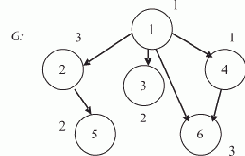
Рис. 7.22.  Информационный граф распараллеливаемой задачи
Алгоритм 8 решения задачи 2 — нахождения графа-решения G'

По алгоритму 5 находим оценку T = T0 минимального времени выполнения данного алгоритма на ВС, содержащей n процессоров.

Опыт подсказывает, что в подавляющем большинстве случаев полученная оценка совпадает с минимальным временем выполнения алгоритма на данной ВС. Чтобы сократить объём вычислений, целесообразно с помощью алгоритма 6 решения задачи 1 установить, способны ли n процессоров выполнить данный алгоритм за время T0. Если T0 — не решение задачи 2, используем следующий метод.

Полагаем ? = ? = 1, T? = ?, где ? — заведомо большое число, например, максимально допустимое на используемой ЭВМ.

Находим наименьшее значение t? такое, что F(?11 , ... , ?1m, t?) = r? > n.
Если такого значения t? нет на первом же шаге сглаживания плотности загрузки (при ? = 1), то значение Tкр — решение задачи 2. Если такого значения больше нет при ? > 1, то увеличиваем значение ? на единицу и полагаем T? = max {?11
, ... , ?1m} , т.е. длине критического пути в графе G', построенном в соответствии с условиями теоремы. Не меняя значение ?, переходим к выполнению 6. (Если T? = T0 + 1, то т.к. T0 — не решение задачи, искать значение T < T? нецелесообразно, т.е. найденное значение T? — решение задачи 2).

Если значение t?, обеспечивающее неравенство в пункте 4, найдено, выделяем множество работ A? = {j?}, ? = 1 , ... , r?, для которых
?1j? - tj? t? < ?1j?.
Множество A? является подмножеством некоторого ПМВНР.

Введём очередную, ещё не испытанную комбинацию r? - n связей, как указано в теореме, так, чтобы длина критического пути в полученном при этом графе G' была меньше T?.

Если такая комбинация связей существует, увеличиваем ? на единицу, уточняем новые значения {?1j} , j = 1 , ... , m, переходим к выполнению 4.

Если такой комбинации связей не существует или все они уже перебраны и при этом ? > 1, уменьшаем ? на единицу и переходим к 6. Если же испытаны все комбинации связей при ? = 1, то последнее значение T? определяет искомое T = T?.

Конец алгоритма.
Пример.
Пусть заданы 6 задач (m = 6), заданы их частичная упорядоченность графом G, заданы времена решения (веса вершин). Требуется найти расписание выполнения этих задач на двух процессорах (n = 2) — такое, чтобы время решений этих задач было минимальным.
Найдём нижнюю оценку длины расписания T.
Первоначально полагаем
По алгоритму 6, испытывая значения функции минимальной загрузки, найдём, что . Произведем единственное уточнение значения
Без учета реально доступного количества процессоров составим (рис. 7.23) временную диаграмму решения всей совокупности задач — такую, при которой каждая из задач решается как можно раньше, и определим загрузку как бы неограниченного числа процессоров:

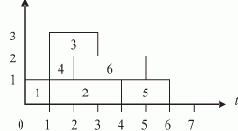
Рис. 7.23.  Временная диаграмма решения задач

находим первый момент времени, при котором по этой диаграмме нам требуется более двух процессоров: при t=1 это количество F(1)=3. Выделим образующие это значение F задачи: {2, 3, 4} и составим матрицу L1 (рис. 7.24а). Первой испытываемой связью является связь 3 2. Диаграмма, соответствующая этой связи, — на рис. 7.24б.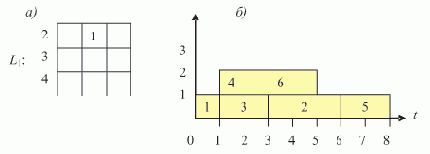

Рис. 7.24.  Первый шаг распределения: а — матрица следования, б — временная диаграмма
Т.к. больше нет значений функции плотности загрузки, превышающих 2, то мы предполагаем возможное решение, но продолжаем перебор связей для поиска более короткого расписания.

следующей испытываемой связью по матрице L1, определяющей длину критического пути, меньшую 8, является связь 4 2. Соответствующее расписание — на рис. 7.25.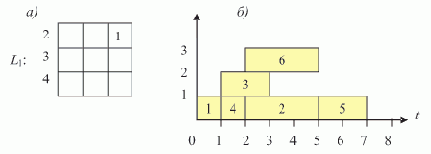

Рис. 7.25.  Введение новой связи: а — матрица следования, б — временная диаграмма

вновь находим первый момент времени, при котором нам требуется более двух процессоров: при t = 2 это количество F(2) = 3. Выделим образующие это значение F задачи: {2, 3, 6} и составим матрицу L2 (рис. 7.26а). Первой возможной связью, не приводящей к длине критического пути, равной 8 или выше, является связь 2 3. Диаграмма, соответствующая этой связи, — на рис. 7.26б.

Рис. 7.26.  Введение последней связи: а — матрица следования, б — окончательный вид временной диаграммы

Т.к. значение функции плотности загрузки больше не превышает значение 2, то мы нашли оптимальное расписание, ибо его длина не превосходит нижней оценки — значения 7.
Задачи точного распараллеливания в настоящей лекции освещаются только для однородных систем исполнителей, когда все такие исполнители "умеют" всё и каждую работу выполняют за одинаковое время. Это предполагает применение методов для однородных вычислительных систем. Однако при более широком применении методов распараллеливания в управлении и экономике актуальна постановка этих задач для неоднородного состава исполнителей, в частности — когда исполнители обладают разной специализацией. Достаточно рассмотреть управление строительством или уборочной кампанией. Алгоритмы точного решения задач распараллеливания для неоднородных систем представлены в [3].

Временные оценки на информационных графах

Информационный граф отображает порядок следования работ. Тогда очевидно, что момент окончания выполнения любой работы (если началом отсчёта времени является момент начала выполнения работ — начало выполнения алгоритма) не может быть меньше максимальной из длин всех путей, которые заканчиваются вершиной, соответствующей этой работе.
Таким образом, для каждой i = 1 , ... , m работы алгоритма, представленного информационным графом, можно найти ранний срок ?1i окончания её выполнения. Если же выполнение алгоритма ограничено временем T < Tкр, то для каждой работы можно найти и поздний срок ?2i(T) окончания её выполнения. Окончание выполнения i-й работы позже этого срока приводит к тому, что выполнение других работ, следующих за данной, не может быть закончено до истечения времени T. Иначе говоря, поздний срок окончания выполнения данной работы не может превышать разности между значением T и максимальной из длин путей, в первую вершину которых входит дуга, что исходит из вершины, соответствующей данной работе. Без задания значения T (ограничения на длительность вычислительного процесса) определение позднего срока окончания выполнения работы не имеет смысла.
При T = Tкр ранние сроки окончания выполнения работ, составляющих критические пути, совпадают с поздними сроками окончания их выполнения.
Прежде чем рассмотреть алгоритм нахождения ранних и поздних сроков окончания выполнения работ по расширенной матрице следования S*, отметим, что учёт транзитивных связей увеличивает число необходимых действий. Так как граф G не содержит контуров, то матрица следования S может быть преобразована в треугольную. Однако при построении алгоритмов решения задач распараллеливания не представляется удобным преобразовывать матрицу следования. Поэтому будем считать, что в общем случае матрица S не треугольная.
Алгоритм 2 нахождения ранних сроков окончания выполнения работ.

Полагаем первоначально ?11 = ?12 = ... = ?1m
= 0.

Производя циклический обзор строк матрицы S, находим очередную из необработанных строк.
Если все строки обработаны, выполнение алгоритма заканчивается.

Пусть j — номер найденной необработанной строки. Если j-я строка не содержит единичных элементов, полагаем ?1j = tj. Переходим к выполнению шага 6.

Если j-я строка содержит единичные элементы, выбираем элементы множества {?11 , ... , ?1m}, соответствующие номерам единичных элементов j-й строки.

Если все выбранные таким образом элементы, образующие множество {?1j(?)}, ? = 1, ... , kj, отличны от нуля, полагаем ?1j = max ?1 j? + tj.

Если хотя бы один из выбранных элементов нулевой (соответствующий ранний срок ещё не найден), выполняем шаг 2.

Обработанную j-ю строку метим, чтобы исключить её повторную обработку. Переходим к выполнению шага 2.

Примечание. Если граф G не содержит контуров, зацикливание при этом невозможно.

Конец алгоритма.

Если матрица S треугольная, то никогда не складываются условия для многократного циклического обзора строк. Тогда ранние сроки окончания выполнения работ находятся за один последовательный просмотр строк матрицы S.

Очевидно, что Tкр = max {?11 , ... , ?1m}.

По матрице S* ( S — треугольная) на рис. 7.5 (граф G — на рис. 7.1) находим

?11 = t1 = 2, ?12 = t2 = 3, ?13 = ?11 + t3

=3, ?14

= ?11 + t4 = 4, ?15 = max {?11, ?12 + t5= 7, ?16 = max {?11, ?14} + t6 = 8, ?17 = max {?12,?14 } + t7 = 6, ?18 = max {?13, ?15, ?16, ?17} + t8 = 9; Tкр = 9.

Чтобы рассмотреть пример с нетреугольной матрицей следования, выберем граф G без контуров с "неправильно" пронумерованными вершинами (рис. 7.10).


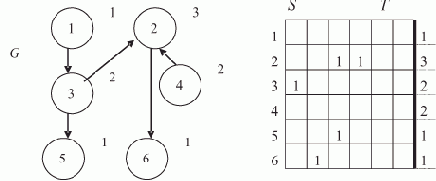
Рис. 7.10.  Информационный граф с не треугольной матрицей следования

После обработки первой строки ?11 = 1. Попытка обработать вторую строку неудачна, т.к. ?13 и ?14 ещё не найдены. После обработки третьей строки ?13 = ?11 + t3 = 3. Обработка четвёртой строки даёт ?14 = 2. После обработки пятой строки ?15 = ?13 + t5 = 4. Попытка обработки шестой строки неудачна, т.к. не найдено значение ?12. Приступаем к следующему циклу обзора необработанных строк S. Обрабатываем вторую строку: ?12 = max {?13, ?14} + t2 = 6.


После обработки шестой строки ?16 = ?12 + t6 = 7. Tкр = 7.

Для удобства представления наряду с другими способами будем пользоваться наглядными диаграммами выполнения работ при заданных значениях времени начала или окончания их выполнения. Работы обозначаются прямоугольниками с постоянной высотой и длиной, равной времени выполнения. Стрелки, связывающие прямоугольники-работы, соответствуют дугам в графе G. На рис. 7.11 представлена диаграмма выполнения работ, отраженных графом G на рис. 7.1 и расширенной матрицей следования на рис. 7.5 — при ранних сроках выполнения работ.


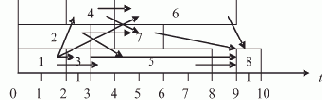
Рис. 7.11.  Временная диаграмма выполнения работ при ранних сроках окончания

Алгоритм 3 нахождения поздних сроков окончания выполнения работ при заданном значенииТ.

Полагаем первоначально ?21(T) = ... = ?2m(T) = 0.

Производя циклический обзор справа налево столбцов матрицы S, находим очередной из не обработанных ещё столбцов. Если все столбцы обработаны, выполнение алгоритма заканчивается.

Пусть j — номер найденного необработанного столбца. Если j-й столбец не содержит единичных элементов, полагаем ?2j(T) = T. Переходим к выполнению шага 6.

Если j-й столбец содержит единичные элементы, выбираем элементы множества { ?21(T) , ... ,?2m(T) }, соответствующие номерам единичных элементов j-го столбца.

Если все выбранные таким образом элементы {?2j?}(T)} {?21(T), ... , ?2m(T)}, ? = 1 , ... , kj, отличны от нуля, полагаем

?2j (T) = min {?2j? (T) - tj? }.

В противном случае выполняем шаг 2.

Обработанный j-й столбец метим с целью исключения его повторной обработки. Переходим к выполнению шага 2.

Конец алгоритма.

Если матрица S — треугольная, то поздние сроки окончания выполнения работ находятся за один просмотр столбцов.

Для матрицы S* (матрица S — треугольная) на рис. 7.5 и для T = 10 за один просмотр находим

?28(10) = 10, ?27(10) = ?28(10) - t8 = 9, ?26(10) = ?28(10)- t8 = 9, ?25(10) = ?28(10) - t8 = 9 , ?24 = min {?26(10), - t6, ?27(10) - t7} = 5, ?23(10) = ?28(10) - t8 = 9, ?22(10) = min {?25(10) - t5, ?27(10) - t7 } = 5, ?21(10) = min {?23(10) - t3, ?24(10) - t4, ?25(10) - t5, ?26(10) - t6} = 3.


Для нетреугольной матрицы S на рис. 7.10 при T = 10 находим ?26(10) = ?25(10) = 10. Обработка четвёртого столбца откладывается, т.к. не найдено значение ?22(10). По этой же причине не обрабатывается третий столбец. После обработки второго столбца находим ?22(10) = ?26(10) - t6 = 9.

Обработка первого столбца невозможна, т.к. ещё не найдено значение ?23(10). Продолжаем циклический обзор столбцов. После обработки четвёертого столбца получаем ?24(10) = ?22(10) - t2 = 6. Обработка третьего столбца даёт ?23(10) = min {?22(10) - t2, ?25(10) - t5} = 6. После обработки первого столбца находим ?21(10) = ?23(10) - t3 = 4.

Диаграммы выполнения работ при поздних сроках окончания, по графам на рис. 7.1 и 7.10, при T = 10 представлены на рис. 7.12 — (а) и (б), соответственно. (Стрелки, соответствующие дугам в графах, опущены в связи с их избыточностью.)


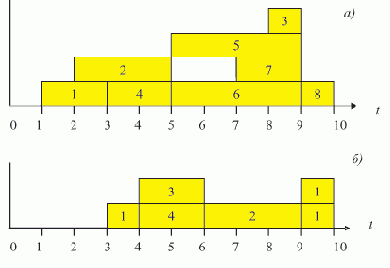
Рис. 7.12.  Диаграммы выполнения работ при поздних сроках окончания: а — для графа на рис. 7.1,б — для графа на рис. 7.10

Пусть ?j — произвольное значение момента окончания выполнения j-й работы, j =1 , ... , m,

?1j ?j ?2j(T) (?j [?1j, ?2j(T)]).

Меняя значения {?j}, j = 1 , ... ,m, но соблюдая при этом порядок следования работ, мы получим множество допустимых расписаний выполнения работ.

Нашей конечной целью является выбор таких расписаний, которые позволяют решить задачи 1 и 2.

Определение 7. Функцию

назовём плотностью загрузки, найденной для значений ?1 , ... , ?m.

Для заданных ?1 , ... , ?m значение функции F в каждый момент времени t совпадает с числом одновременно (параллельно) выполняющихся в этот момент работ.

Например, по диаграмме на 7.11, т.е. для ?1 = ?11, ?2 = ?12, ... , ?8 = ?18, функция F(2, 3, 3, 4, 7, 8, 6, 9, t) имеет вид, представленный на рис. 7.13а. Для допустимого расписания, определяемого набором значений ?1 = 2, ?2 = 4, ?3 = 3, ?4 = 4, ?5 = 8, ?6 = 9, ?7 = 7, ?8 = 10, функция F(2, 4, 3, 4, 8, 9, 7, 10, t) имеет вид, представленный на рис. 7.13б.



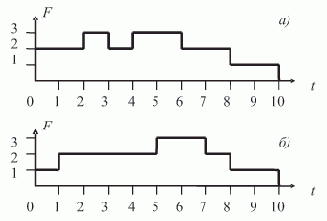
Рис. 7.13.  Графики функции: а — для ранних сроков окончания работ,,б — для некоторого допустимого расписания

Для графического представления функции F удобно пользоваться временной диаграммой, которая для второго случая, например, имеет вид, представленный на рисунке 7.14..


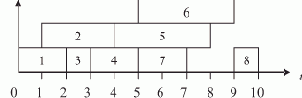
Рис. 7.14.  Временная диаграмма функции F

Пусть данный граф G, в котором учтены транзитивные связи, образует l полных множеств взаимно независимых работ (ПМВНР). (Каждая пара таких множеств может иметь непустое пересечение.) Обозначим ri, i = 1 , ... , l, число работ, образующих i-е полное множество и найдём

R = max {r1 , ... , rl}.

Тогда

т.к. возможно и такое распределение выполняемых работ во времени, задаваемое набором ?1 , ... , ?m, (т.е. допустимое расписание), когда на каком-то отрезке времени выполняются все работы, составляющие ПМВНР с числом R работ.

Например, для графа на рис. 7.1 мы нашли ПМВНР {3,5,6,7}, включающее четыре работы. Тогда существует допустимое расписание, например, ?1 = 2, ?2 = 3, ?3 = 5, ?4 = 4, ?5 = 8, ?6 = 8, ?7 = 6, ?8 = 9 такое, при котором максимальное значение плотности загрузки F равно четырём (рис. 7.15).


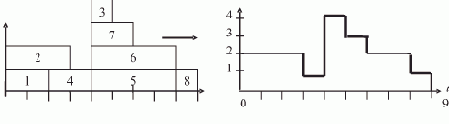
Рис. 7.15.  Максимальное значение плотности загрузки

Таким образом, справедливо утверждение

Лемма. Минимальное число n процессоров одинаковой специализации и производительности (т.е. в однородной ВС), способных выполнить данный алгоритм за время T Tкр, не превышает R = max {r1 , ... , rl }, где ri , i = 1 , ... , l, — число работ, входящих в i-е ПМВНР, которое составлено по взвешенному графу G, соответствующему этому алгоритму.

Определение 8. Функцию

назовём загрузкой отрезка [?1, ?2] [0,T] для заданного допустимого расписания ?1, ... ,?m.

Функция Ф определяет объём работ (суммарное время их выполнения) на фиксированном отрезке их выполнения при заданном допустимом расписании.

Так, для отрезка времени [0, 4] [0, 10] на рис. 7.13а Ф = 10; для отрезка времени [1, 3] на ррис. 7.13б Ф= 4; для отрезка времени [2, 5] на рис. 7.15


Ф = 10 и т.д.

Определение 9. Функцию

назовём минимальной загрузкой отрезка [?1, ?2] [0, T].

Функция определяет минимально возможный объём работ, который при данном T и при различных допустимых значениях (расписаниях) ?1 , ... , ?m

должен быть выполнен на отрезке времени [?1, ?2] [0, T]. Это означает, что как бы мы не планировали вычислительный процесс, который должен быть закончен к моменту времени T, т.е. какой бы набор значений ?1 , ... , ?m

мы не выбрали, объём работ, выполняемых на отрезке времени [?1, ?2], не может быть меньше значения (T) = (?1, ?2).

Теорема 1. Для того чтобы T было наименьшим временем выполнения данного алгоритма однородной вычислительной системой, состоящей из n процессоров, либо чтобы n процессоров было достаточно для выполнения данного алгоритма за время T, необходимо, чтобы для данного отрезка времени [?1, ?2] [0, T] выполнялось соотношение

(7.1)

Доказательство. Нетрудно видеть, что если при данном наборе ?1 , ... , ?m — сроках окончания выполнения работ, в том числе и при таком наборе, при котором обеспечивается минимальное или заданное T = max {?1

, ... , ?m}, для реализации алгоритма достаточно n процессоров, то

Отсюда, для любого отрезка времени [?1, ?2] [0, T]

что и требовалось доказать.

Необходимость, но не достаточность условия (7.1) покажем на примере. Пусть алгоритму соответствует граф G на рис. 7.16а. Пусть T=3, и одна из возможных диаграмм выполнения алгоритма — на рис. 7.16б.


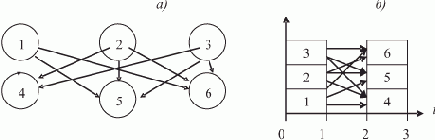
Рис. 7.16.  Пример: минимальная плотность загрузки не соответствует действительной: а — информационный граф, б — временная диаграмма загрузки

Оценим на основе (7.1) число n процессоров, достаточное для выполнения алгоритма в указанное время. Из (7.1) имеем общее соотношение

(7.2)

Для получения полной оценки надо перебрать все отрезки [?1, ?2] [0, T] т.е.

(7.3)

Проанализируем все возможные отрезки [?1, ?2] [0, 3] : (3)(0, 1) = (3)(1, 2) (3)(2, 3) = 0, (3)(0, 2) = (3)(1, 3) = 3, (3)(0, 3) = 6.


Находим минимальное n = 2, удовлетворяющие (7.3). Однако из рисунка видно, что не существует плана выполнения работ на двух процессорах за время T=3. Минимально достаточное число процессоров здесь n = 3.

Функция (T)(?1, ?2) минимальной загрузки отрезка времени является одним из основных средств оценки предпринимаемых действий при решении задач распараллеливания. Поэтому ниже будет дан алгоритм нахождения её значения.

Предварительно определим функцию

Тогда значение ?(?1j - ?1) характеризует условный объём части работы j на отрезке времени [?1, ?2] при условии ?1j

- tj ?1 и при максимальном смещении времени выполнения работы j влево (рис. 7.17а).

Значение ? (?2 - ?2j(T) + tj) характеризует аналогичный объём работы j при максимальном смещении времени выполнения работы j вправо. Это соответствует, например, ситуации, изображённой на рис. 7.17б.


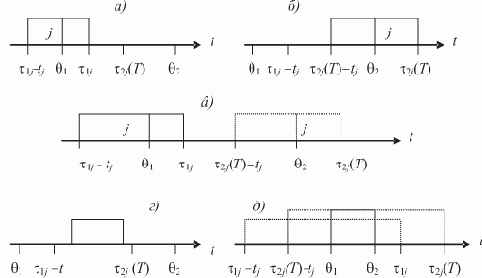
Рис. 7.17.  Нахождение минимальной плотности загрузки отрезка: все различные случаи соотношения времени выполнения работ и сроков

Если для работы j оба указанных выше значения функции ? отличны от нуля, но не превышают значение tj и ?2 - ?1, то максимально разгрузить отрезок [?1, ?2] от работы j можно смещением времени его выполнения в сторону, обеспечивающую меньшее из двух указанных выше значений ? (рис. 7.17в).

Существуют два случая, когда работа j не может быть хотя бы частично смещена с отрезка [?1, ?2] :

а) ?1 ?1j - tj < ?2j (T)

?2, в этом случае очевидно, что tj ?2 - ?1

(рис. 7.17г), и объём работы j, выполняемой на отрезке, совпадает с объёмом tj всей этой работы;

б) ?1j ?2 ? ?2j(T) - tj ?1, в этом случае очевидно, что tj ?2 - ?1

(рис. 7.17д), и объём части работы j, выполняемой на отрезке [?1, ?2] совпадает со значением ?2 - ?1.

Приведённый ниже алгоритм объединяет все возможные указанные выше случаи.

Алгоритм 4 нахождения значения функции (T)(?1, ?2).

1. Предполагаем, что для каждой работы j = 1, ... , m, известны значения tj, ?1j, ?2j(T). Полагаем равным нулю значение переменной .

2. Организуем последовательный анализ работ j = 1, ... , m.


3. Для каждой работы j полагаем

:= + min {? (?1j - ?1), ?(?2 - ?2j(T) + tj), tj , ?2 - ?1}.

После перебора всех работ = (T)(?1, ?2).

Конец алгоритма.

Выше было получено соотношение (7.2) , которое можно использовать для нижней оценки количества n процессоров, необходимых для выполнения данного алгоритма за время, не превышающее T.

Приведём аналогичное соотношение для нижней оценки минимального времени Т.

Теорема 2. Пусть заданный алгоритм выполняется на ВС, состоящей из n процессоров, и T* — текущее значение оценки снизу времени выполнения алгоритма. Пусть на отрезке времени [?1, ?2] [0, T*] выполняется соотношение

(T*)(?1,?2) - n(?2 - ?1) = d > 0.

Тогда минимальное время T выполнения алгоритма удовлетворяет соотношению

(7.4)

Теоремы 1 и 2 на основе анализа такой локальной характеристики параллельного алгоритма, как значение функции минимальной загрузки отрезка, предлагают способы оценки снизу ресурсов, необходимых для реализации каждого заданного алгоритма:

числа n процессоров при заданном ограничении на длительность T процесса;

минимального времени T, необходимого для реализации данного алгоритма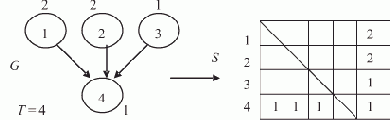 при заданном числе n процессоров.

Рис. 7.18.  К примеру нахождения нижней оценки числа исполнителей

Параллельное программирование

Централизованное диспетчирование

В более сложном виде задача диспетчирования возникает в централизованных ВС. В чем она заключается?
Пусть некоторый супервизор, например, в системе реального времени, определил множество информационно взаимосвязанных задач (частично — упорядоченное множество задач), которые должны решаться циклически, а возможно, и единственный раз процессорами ВС. Известны временные оценки решения задач.
Пусть задан взвешенный ориентированный граф, не содержащий контуров, отражающий частичную упорядоченность работ (задач, процессов, макроинструкций, процедур, операторов и т.д.), которая обусловлена их информационной преемственностью (рис. 8.3).

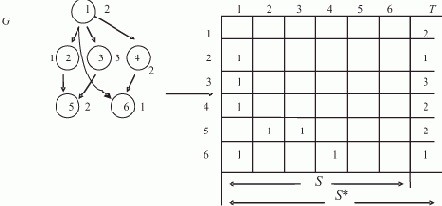
Рис. 8.3.  Информационный граф и расширенная матрица следования

Показана соответствующая ему матрица следования S и расширенная матрица следования S*, содержащая и столбец весов.
Универсальным критерием, используемым при решении задачи диспетчирования как задачи распараллеливания, является минимум времени выполнения совокупности работ, распределяемых между процессорами.
Формально: пусть задано множество работ A = {1 , ..., m} и известно множество временных оценок этих работ T = {t1 , ..., tm}, а также известна частичная упорядоченность, задаваемая матрицей следования S. Пусть ВС — однородная (т.е. все процессоры обладают одинаковой производительностью) и содержит n процессоров. Пусть в результате распределения множества работ A между n процессорами каждый (i-й) процессор оказался занятым решением задач в течение времени Ti. Тогда время решения всей совокупности задач

Задачей диспетчера является распределение работ 1,..., m между процессорами, обеспечивающее
Далее будут изложены достаточно простые диспетчеры на основе эвристических методов решения задачи оптимального распараллеливания — задачи высокой сложности. Такие алгоритмы используют достаточно эффективные решающие правила, приближающие расписания к оптимальным.

Децентрализованное диспетчирование в многоканальном и многоциклическом режиме

Рассмотрим схему организации параллельного вычислительного процесса в реальном времени.
Система управления обслуживает в многоканальном режиме ряд однотипных объектов. Одновременно обслуживаемые объекты могут находиться на разных стадиях обслуживания. По каждому объекту циклически и в разных комбинациях решаются задачи из некоторого заранее установленного множества информационно взаимосвязанных задач. Частичная упорядоченность задач задается расширенной матрицей следования S*.

Рассмотрим случай, когда задачи решаются в цикле одной длительности.
Супервизор формирует матрицу S', которая отражает множество решаемых задач по всем объектам (или по всем занятым каналам обслуживания), обслуживаемым в данное время, и список или очередь Q, содержащий информацию о решаемых задачах (рис. 8.4).

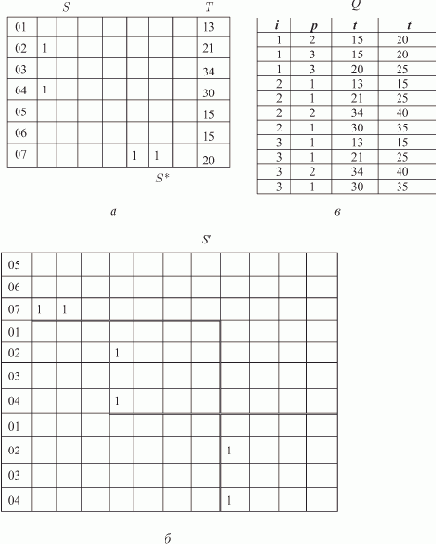
Рис. 8.4.  Информация для одноциклического режима обслуживания

(Для этого из матрицы S* для каждого объекта исключаются строки и столбцы, соответствующие нерешаемым задачам, и блочно-диагональным наращиванием строится S'.)
Каждая задача характеризуется именем, номером i канала или объекта, по которому она решается, относительным приоритетом p, значением t времени решения, контрольным временем t0, по истечении которого следует сделать вывод об аварийной ситуации.
При обращении процессора к очереди, назначение очередной задачи на процессор производится на основе анализа S*. Из множества задач, которым соответствуют нулевые строки этой матрицы, выбирается еще не назначенная задача с максимальным приоритетом (минимальное значение p) из тех, которые по времени выполнения укладываются в ресурс процессора в цикле (см. далее). Если таких задач с одинаковым приоритетом несколько, из них выбирается задача с максимальным временем выполнения. Назначенная задача отмечается, чтобы исключить повторное назначение.
После решения любой задачи и исключения информации о ней из S* могут оказаться "открытыми" задачи, обладающие более высоким приоритетом, чем некоторые из тех, которые уже решаются.
В этом случае возможен один из вариантов, когда диспетчер того процессора, на котором закончилось решение некоторой задачи, после назначения (себе) очередной задачи производит попытку дополнительного назначения другим процессорам. Находится готовая к решению задача с максимальным приоритетом и для него — с максимальным временем t. Процессоры последовательно опрашиваются. По опросу прерывается работа того процессора, который решает задачу с приоритетом меньшим, чем приоритет найденной задачи, и с текущим ресурсом времени в цикле , превышающим t. Ему выдается сигнал прерывания, по которому он выполняет прерывание и обращается к очереди. Тогда эта задача будет назначена вместо прерванной.

Попытка дополнительного назначения производится до тех пор, пока не будут исчерпаны все задачи, готовые к решению (входы S*, соответствующие еще не назначенным задачам), или пока не будет закончен однократный опрос всех процессоров.

Циклическая работа процессоров организуется с помощью прерывания от системы синхронизации (таймера или СЕВ). В этом случае восстанавливается исходный вид матрицы S* и очередь Q. Процесс решения задач повторяется, если супервизор не внес коррективы в их состав.

Многоциклический режим. Пусть часть задач решается в цикле длительности k1, часть — в цикле длительности k2 и т.д. Всего — r длительностей, и k1 < k2 < ... < kr. (Обычно k1 = 1.) Через интервалы, кратные , в ВС формируются сигналы прерывания, анализируемые диспетчерами процессоров. Если k? > k?, то все задачи, решаемые в цикле k?, обладают более высоким приоритетом, чем все задачи, решаемые в цикле k?.

При составлении комплексного задания объединяют его части, относящиеся к циклам одинаковой длительности. Каждая часть заканчивается признаком "конец задания для kj" j = 1 , ... , r (рис. 8.5). По этому признаку после выполнения всего задания для данного цикла и поступления сигнала от системы синхронизации о начале следующего цикла этой же длительности восстанавливается исходный вид соответствующей части задания.


После этого диспетчеры производят дополнительное назначение в соответствии с готовыми к решению более приоритетными задачами, т.е. начинают новый цикл по возможности с более приоритетных задач.


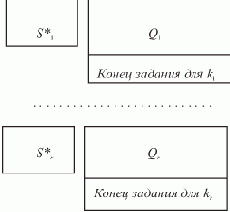
Рис. 8.5.  Многоциклический режим параллельного решения задач

Выбор процессором новой задачи, как говорилось выше, производится с учетом того ресурса времени, которым обладает данный процессор до момента обязательного окончания решения данной задачи. Должна учитываться необходимость прерывания решения этой задачи ради задач с более высоким приоритетом, т.е. ради задач, решаемых в циклах меньшей длительности.

Как же считается и учитывается этот ресурс? Рассмотрим его как переменный ресурс времени Rij, которым располагает i-й процессор, i = 1, ... , n, в цикле длительности kj , j = 1 , ... , r.

Пусть первоначально, до назначения на процессор задач i-й процессор в цикле длительности k1 располагал ресурсом Ri1 = k1, в цикле длительности k2

— ресурсом Ri2 = k2 и т.д. Пусть на процессор для решения выбрана задача с временем решения t. Пусть она решается в цикле длительности kj . Ее назначение не влияет на порядок решения задач в циклах меньшей длительности, т.к. они обладают более высоким приоритетом. Однако при последующем назначении на этот же процессор задач, решаемых в цикле этой и большей длительности, необходимо учитывать решение задачи — с равным или большим приоритетом.

Запишем оператор определения нового значения вычислительного ресурса в цикле длительности kj и в циклах большей длительности после единичного назначения на этот же процессор в цикле kj



Здесь ресурс оценивается приближенно, без учета дискретности работ, соразмерности длительности циклов и неточности определения t.

Таким образом, прежде чем производить назначение другой задачи,?, решаемой в цикле длительности kj ?, на i-й процессор, необходимо проверить, располагает ли он ресурсом Rij t?? Если располагает, назначение производится, после чего значения ресурса для l j уточняются.Если не располагает, производится поиск подходящей задачи.

Это и было отражено выше при рассмотрении назначения в одно- и многоциклическом режиме решения задач.

Классификация

ВС делятся на централизованные и децентрализованные. Это связано с реализованными в них способами управления, или диспетчирования.
Централизованное диспетчирование (ему соответствует централизованная ВС) реализуется управляющим процессором или периодически включаемой в состав очереди задачей наивысшего приоритета. При централизованном диспетчировании существует возможность более полного охвата и прогнозирования состояния всех средств ВС и тщательного выбора плана дальнейшей загрузки процессоров.
Децентрализованное диспетчирование (ему соответствуют децентрализованные ВС) предусматривает возможность самостоятельного обращения каждого процессора к общей очереди для выбора заданий. Обращение к очереди происходит по мере освобождения процессора или по прерыванию. Учет ресурсов всей ВС и оценка в связи с этим различных вариантов назначения отсутствуют. Полностью реализуется виртуальность процессоров. Сокращаются затраты времени (полезной производительности) на диспетчирование, но не используются методы оптимального планирования совместной работы процессоров. Децентрализованное диспетчирование обеспечивает высокую надежность, живучесть ВС. Однако полностью независимой работы процессоров добиться нельзя хотя бы по причине необходимости контроля и реконфигурации ВС при отказе ее модулей, а также в связи с необходимостью возврата заданий в очередь с отказавших процессоров для их перезапуска.
Таким образом, в чистом виде децентрализованное диспетчирование не применяется.

Комбинированное диспетчирование в ВС с очередью

Рассмотрим более детально, применительно к сложным системам обработки информации или к АСУ, как организуется параллельный процесс в таких системах. При этом мы увидим, что в реальных системах принципы централизованного и децентрализованного управления причудливо переплетаются. Будем ориентироваться на ВС с очередью, обеспечивающей виртуализацию вычислительного ресурса (процессоров), что характерно для семейства "Эльбрус". Такие ВС в значительной степени обеспечивают децентрализованное диспетчирование.
Итак, специально организованная программа, выступающая как самостоятельно, так и во взаимодействии с другими подобными программами, как указывалось выше, соответствует некоторому процессу. Если данный процесс прерывается, то текущее состояние стека процессора, который его выполнял, а также состояние ряда регистров необходимо запомнить. Поставим в соответствие состояние стека процессора, выполняющего данный процесс, в том числе то состояние, которое предшествует выполнению (если процесс только сформирован, но еще не начал выполняться), этому процессу, дополнив его состоянием необходимых регистров. Иными словами, введем понятие стека процесса, которым обладает каждый процесс, о чем говорилось выше. Стек процесса может переходить из пассивного состояния в активное и обратно. Отсюда — понятия активного и пассивного стека процесса. Активный стек связан с оборудованием или "наложен" на оборудование и, следовательно, находится в состоянии изменения. Пассивный стек — это "моментальный снимок", временной срез прерванного (или не начавшегося, или кончившегося) процесса, ждущего дальнейшего выполнения (или уничтожения).
Таким образом, стек процесса отражает текущее состояние процессора, выполняющего данный процесс. Стек процесса можно запомнить на момент прерывания, и хранимой в нем информации при обратном "наложении" на оборудование — на любой свободный процессор достаточно для продолжения выполнения этого процесса. Ранее рассматривалась структура пассивного стека процесса.

Стек процессора обладает активным оборудованием, на которое налагается стек процесса для его активизации (рис. 8.6), т.е. для выполнения процесса.


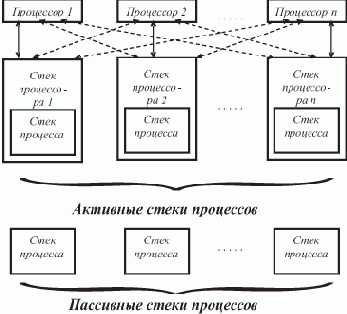
Рис. 8.6.  Комбинированное диспетчирование в ВС с очередью

Следовательно, рассматривая абстрактно стеки процессов, можно говорить о закреплении за ними ресурсов (процессоров) для их активизации. При этом исключается необходимость привязки к конкретным стекам процессоров. Реализуется виртуальный вычислительный ресурс.

Ранее говорилось, что информационной основой работы процессоров ВС является очередь процессов "к процессору", которую составляют пассивные стеки процессов. Из очереди процессов процессоры выбирают задания по мере окончания выполнения принятых ранее или при необходимости их прерывания. Очередь процессов может формироваться на основе любого числа элементов процессов. Естественно, при реализации это число приходится ограничивать. В соответствии с готовностью к выполнению и выполнением различают три состояния процессов: активен, т.е. стек данного процесса находится на стеке одного из процессоров и, следовательно, этот процесс выполняется; готов к выполнению, т.е. данный процесс не выполняется только из-за отсутствия свободного процессора; ждет, т.е. процесс не может выполняться, пока не произойдет некоторое событие, обусловленное приоритетом или информационной взаимосвязью процессов. В частности, если в ВС реализован механизм семафоров, регулирующий частичную упорядоченность процессов, то процесс может находиться в состоянии ожидания открытия семафора ("висеть" на семафоре).

Очередь процессов формируется в виде списка, где готовые к выполнению процессы выстраиваются по приоритетам. Каждый процесс, еще не выполнявшийся или прерванный, представлен своим стеком. Ждущие процессы, по мере выполнения условий задержки (например, открытия семафоров), занимают место в соответствии со значением приоритета (или вырабатываемым значением приоритета) в очереди процессов. Процессор выбирает процесс из головы очереди.


В каждом элементе очереди хранится указатель на очередной элемент. Благодаря этим указателям очередь сплетается в нужном порядке.

Исследуя динамическое управление составом очереди и порядком следования в ней процессов, можно организовать различные способы работы ВС. Например, можно периодически подставлять в очередь процессы, реализующие процедуры контроля состояния средств ВС, опроса терминальных устройств, работ по организации памяти, уничтожения процессов и т.д. Возможны различные альтернативные способы влияния на состав очереди. Способ постановки в очередь особенно оправдан при низких требованиях к точности определения момента инициализации работ. Если такие требования высоки, то на помощь приходит механизм прерываний.

На рис. 8.7 отражен текущий вид очереди, а также те связи (штриховыми линиями), которые возникнут, если откроются семафоры A и B выполняемыми на процессорах процессами.


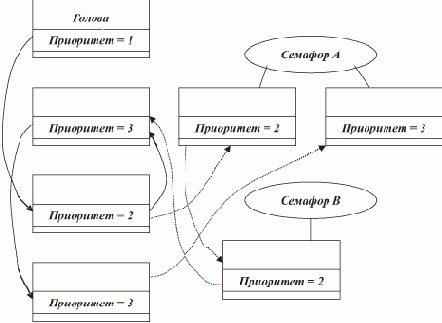
Рис. 8.7.  Учёт приоритета задач в очереди

Приоритеты процессов могут периодически изменяться, если это необходимо. Например, система может повышать приоритет тех процессов, у которых достаточно частый обмен информацией с внешним полем. Это увеличивает эффективность мультипрограммной обработки, т.к. прерывание для обменов все равно потребует включения в решение других задач, а окончание обменов позволит вернуться к решению прерванных.

Для повышения надежности и универсальности используемых ресурсов стеки процессоров могут быть нежестко закреплены за процессорами (см. идею решающих полей!). В стеке процессора в основном концентрируются устройства памяти процессоров, основные регистры, над которыми производятся операции. Операционные устройства могут быть отделены от собственно процессора и рассматриваться отдельно. Собственно процессором остается устройство управления, ведающее обработкой потока инструкций, их назначением для выполнения. Это допускает перекоммутацию (показана штриховой линией на рис. 8.8) связи процессор-стек процессора в случае отказов процессоров, т.к.


стек отказавшего процессора соответствует пассивному стеку некоторого процесса. При этом может быть учтен приоритет решаемых процессорами задач.


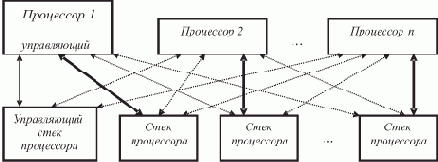
Рис. 8.8.  ВС с управляющими процессором и стеком

Для оперативного продолжения одними процессорами работ, выполнение которых уже начато на других процессорах, целесообразно, чтобы стеки процессоров составляли общую память, доступную всем процессорам. В то же время, эти стеки должны быть в разных блоках этой памяти, что должно допускать одновременное обращение, т.е. должны быть минимизированы взаимные помехи при работе процессоров. Связь с закрепленными за ними стеками процессоры могут осуществлять с помощью специально выделенных базовых регистров, адреса которых различимы для специальных команд, ведающих коммутацией, и неразличимы для процессоров: часть адреса такого регистра является общей для всех процессоров.

В частности, возможна следующая процедура продолжения работы ВС в случае отказа или отключения одного из процессоров.

Прерывается работа головного процессора.

Запускается на нем процедура анализа активных процессов.

Данная процедура находит среди всех активных стеков стек выполняемого процесса с минимальным приоритетом. При этом возможны два случая:

процесс из стека отказавшего процессора оказывается в числе процессов с минимальным приоритетом, тогда этот процесс переводится в очередь процессов;

минимальным приоритетом обладает активный процесс, не выполнявшийся на стеке отказавшего процессора. Тогда изменяется содержимое базового регистра выполнявшего этот процесс процессора для подключения его к стеку отказавшего процессора, стек прерванного процесса становится пассивным и переводится в очередь.

Т.к. внутри системы накапливаются разнообразные функции управления (режимами прохождения задач, ресурсами, обеспечением надежности), то слежение за работой ВС должно осуществляться с устойчивым периодом. Одним из вариантов такого устойчивого вмешательства управляющих средств является не только назначение одного из процессоров управляющим, но и формирование в системе специального управляющего стека процессора (рис. 8.8).


После прерывания управляющего процессора с частотой, с которой производится анализ состояния системы, осуществляется коммутация этого процессора с управляющим стеком процессора, чтобы избежать работы стандартной процедуры переключения на новый вид работ, которая может быть значительно более трудоемкой. В управляющем стеке процессора работы по управлению могут быть всегда подготовлены (в результате предыдущего включения) к продолжению с момента переключения на них управляющего процессора.

Элемент же децентрализованного управления ВС может осуществляться с помощью периодического включения в состав очереди управляющего процесса, объединяющего ряд процедур управления. При каждом включении этого процесса подготавливается его следующее включение вновь. С таким процессом может быть связан семафор C, открытие которого может производиться по достижении таймером некоторого значения времени T = t + ?, где t — время настоящей активации управляющего процесса; ? — период его активации (период или такт управления). Тогда управляющий процесс должен начинаться с процедуры ЖДАТЬ (С,Т) и включать в себя процедуру ЗАКРЫТЬ (С).

Очевидно, что такое решение не обеспечивает оперативной и синхронной работы средств ВС и чревато возможностью отказа ВС без выхода на процедуры управления. Поэтому подстановку управляющих процессов в очередь все же целесообразно поручить управляющему процессору (считая, что им может быть один из процессоров ВС, решающий и основные задачи из очереди). На рис. 8.9 это — управляющие процессы УП1 и УП2. Но это, как говорилось ранее, — когда отсутствуют жесткие требования к моменту принятия решения.


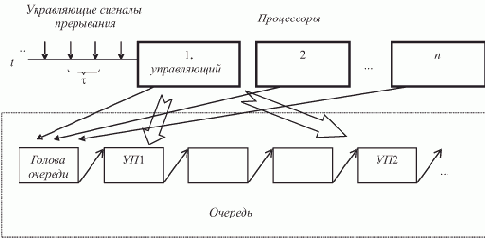
Рис. 8.9.  Два управляющих процесса в очереди

Управляющий процессор реагирует на сигналы прерывания, поступающие в жестком временном режиме — с периодом ?. По поступлении на управляющий процессор сигнала прерывания может быть произведена его перекоммутация на управляющий стек процессора или подстановка в очередь необходимого управляющего процесса. В этом случае обработка управляющих процессов производится так же, как и других процессов, теми процессорами, которые их выбрали для выполнения в соответствии с виртуализацией вычислительного ресурса.


Подводя итог анализу способов организации управления вычислительным процессом в ВС, можно выделить три возможности:

1) управление через очередь, при котором управляющий процесс периодически подставляется в очередь и реализуется процессором, выбравшим его в соответствии с дисциплиной обслуживания очереди. Такой способ управления приемлем, например, для таких работ, как реорганизация памяти, оценка состояния средств и др.;

2) выполнение одним из процессоров функции головного или управляющего. Его работа по обслуживанию очереди периодически прерывается для выполнения функций управления ВС;

3) наличие в системе специального управляющего процессора (иногда называемого ХОСТ-процессором), в силу назначения и исполнения не участвующего в обслуживании очереди. В многопроцессорных ВС, совмещающих различные режимы обработки информации и нуждающихся в сложном планировании использования ресурсов, целесообразно включение в состав ВС специализированных управляющих процессоров.

Общая схема параллельных вычислений при обслуживании потока заявок (в АСУ)

Рассмотрим схему организации параллельного вычислительного процесса, характерную для автоматических или автоматизированных систем управления (рис. 8.1).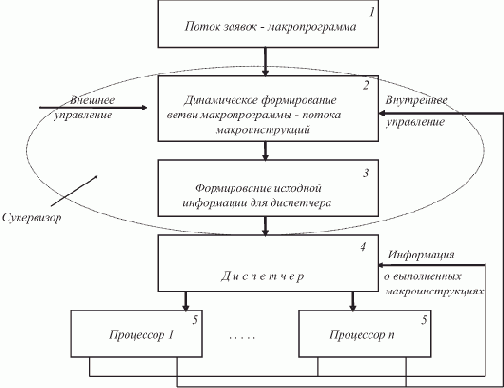

Рис. 8.1.  Схема параллельного вычислительного процесса
Общий алгоритм функционирования АСУ в виде макропрограммы отображен блоком 1.
Каждая макроинструкция может заключать большой объем работ. Это — отдельные операторы, задачи (функциональные модули), задания, процессы и др. Макропрограмма либо содержит макроинструкции, которые соответствуют логическим операторам, влияющим на выбор ее ветви, либо имеет специальный блок управления. В результате выполнения этих операторов формируется (блок 2) поток макроинструкций (очередь), подлежащих выполнению процессорами. При этом могут учитываться значения логических переменных, как рассчитанные по макропрограмме (внутреннее управление), так и выработанные на основе внешнего воздействия: управляемым объектом, параметрами управляемого технологического процесса, оператором с пульта или терминала. Т.е. на этом уровне вырабатывается непосредственно поток заданий.
Затем (блок 3) формируется некоторая интерпретация потока заданий (макроинструкций) для диспетчера.
Блоки 2 и 3 могут входить в состав супервизора, определяющего необходимые действия системы управления в процессе ее функционирования.
Диспетчер 4 распределяет работы между процессорами 5 — производит распараллеливание. При этом естественно используется обратная связь от процессоров с сообщениями о ходе выполнения назначенных макроинструкций. Макроинструкции, поступившие на процессор в результате распараллеливания, выполняются в режиме интерпретации - запускаются соответствующие заранее загруженные, т.е. известные всем процессорам, программы (процессы).

Особенности параллельного вычислительного процесса в системе реального времени

Работа АСУ в системе реального времени характеризуется жесткой временной привязкой приема и выдачи информации, поскольку речь идет об управлении некоторыми объектами (например, движением летательных аппаратов) или технологическими процессами.
В целом АСУ реального времени на основе использования ВС является многоканальной системой массового обслуживания, поскольку, как правило, управление производится сразу большим числом объектов (множеством летательных аппаратов, множеством вырабатываемых изделий и т.д.). Общая схема организации вычислительного процесса та же, что и выше.
Однако, чтобы нагляднее подвести к проблемам построения управляемого параллельного вычислительного процесса, рассмотрим, как решаются задачи в реальном времени.
Возьмем возможную временную диаграмму (рис. 8.2).

Рис. 8.2.  Схема параллельных вычислений в реальном времени
Пусть ВС состоит из двух процессоров. Общий алгоритм управления разбивается на частные задачи, решаемые в циклах двух длительностей 1 и 2 , пусть 2 = 21. Информационно зависимые задачи, решаемые в цикле длительности 1, отражены графом G1, а задачи, решаемые в цикле длительности 2, — графом G2. Графы — взвешенные: вес вершины равен условному времени решения соответствующей задачи, что отражено на диаграмме.
Примечание. О многоциклическом режиме решения задач в АСУ.
Предположим, мы управляем каким-то "быстрым" объектом или процессом. Нам надо с большой частотой выдавать управляющие воздействия. Они вырабатываются (на некотором временном интервале) по одним и тем же алгоритмам, т.е. циклически решаются одни и те же задачи. Их решение привязывается к сигналам прерывания, которые выдаются с одной и той же частотой. Но могут решаться периодически и другие задачи, для точности результатов которых достаточна более низкая частота: задачи оценки состояния среды, меняющейся плавно, задачи отображения и т.д. Таким образом, в целом в системе одновременно циклически решаются много задач, но в циклах разной длительности.
В общем случае решаемые задачи информационно взаимозависимы.

Строго говоря, они взаимозависимы и по управлению, т.е. от результатов решения одних задач может зависеть и состав далее решаемых задач. Мы будем считать, что состав задач определен на протяжении значительного времени функционирования. Более того, состав решаемых задач определяет супервизор, и внутри одного цикла (или такта) управления этот состав не меняется. Информационная зависимость отображается взвешенным информационным графом, как представлено в примере.

Процессор передачи данных ППД для каждого цикла управления в последовательности, показанной на диаграмме, производит опережающий прием исходной информации в память ВС и последующую выдачу результатов вычислений на объекты управления. Разная толщина стрелок показывает, что объем обмена различен для циклов разной длительности.

Из диаграммы видно, что в момент начала цикла длительности 2, а, следовательно, и цикла длительности 1, включается супервизор (отмечен черным), функции которого значительно шире, чем при включении в начале только цикла длительности 1

(отмечен светлым). В результате его работы возможна смена состава решаемых задач. Если в системе есть и диспетчер, его работа может быть учтена увеличением времени работы супервизора.

Предполагают, что задачи, решаемые в каждом цикле меньшей длительности (1), обладают более высоким приоритетом, чем задачи, решаемые в циклах большей длительности (2).

Загрузка процессоров ВС может быть организована по правилам мультипрограммной обработки с учетом частичной упорядоченности задач и их относительного приоритета.

Процессор 1 сначала выбирает для решения задачу 1. Из готовых к решению задач процессор 2 может выбрать лишь задачу 6. После решения задачи 1 появляется возможность решения высокоприоритетных задач 2 и 3. Задача 2 выбирается процессором 1, а процессор 2 прерывает задачу 6 и приступает к решению задачи 3. (Неизбежен циклический анализ очереди на появление задач, приоритет которых выше приоритета решаемых задач.) После решения задачи 3 начинается решение задачи 5, а после решения задачи 2, с учетом того, что к этому моменту решена и задача 3, начинается решение задачи 4.


После окончания решения задачи 5 продолжается решение задачи 6, затем начинается решение задач 7 и 8. Однако их решение прерывается началом выполнения следующего цикла длительности 1, в котором вновь воспроизводится план решения задач 1--5. Лишь во время решения процессором 1 задачи 1 продолжается решение задачи 7 процессором 2. В соответствии с приоритетом решение задач 7 и 8 заканчивается. В следующем цикле длительности 2 весь рассмотренный план решения задач 1--8 повторяется, и так — до изменения состава задач в соответствии с условиями работы управляющей системы.

Из примера видно, что частичная упорядоченность задач (задан обязательный порядок следования некоторых задач, обусловленный информационной преемственностью) препятствует полной загрузке процессоров, несмотря на высокие требования к использованию всех вычислительных ресурсов. Она определяет основную трудность решения задач оптимального распараллеливания.

Распараллеливание в МВК. Семафоры

Распараллеливание для полного использования ресурсов МВК осуществляется двумя путями:

на основе естественного существования независимых задач пользователей;

на основе существования сложных программных систем, которые состоят из взаимосвязанных процессов, допускающих параллельное выполнение.

Синхронизация информационно взаимосвязанных процессов производится с помощью механизма семафоров.
Пусть существует множество величин - примитивов синхронизации, имеющих тип "семафор" и принимающих в простейшем случае два значения: "открыт" и "закрыт". (В другой версии семафор — счетчик; закрытию соответствует его увеличение на единицу, а открытию — уменьшение на единицу.)
В состав ОС входит ряд процедур, которые обеспечиваются аппаратными средствами и отражаются на входном языке, т.е. доступны пользователю. Минимально необходимый набор таких процедур:
ОБЪЯВИТЬ (С) — объявляется список семафоров C, выделяется память и задается тип переменной при трансляции.
ЗАКРЫТЬ (С) — присваивает семафорам, перечисленным в списке C, значение "закрыт".
ЖДАТЬ (С) — в случае, если в C указаны семафоры со значением "закрыт", прерывает выполняемый процесс. Стек процесса условно дополняет очереди к закрытым семафорам, перечисленным в списке C. Таким образом, если с данной процедуры начинается выполнение некоторой работы, то оно будет поставлено в зависимость от условий выполнения каких-то других работ. Концом выполнения процедуры является переход к анализу очереди процессов для последующей загрузки процессора.
ОТКРЫТЬ (С) — семафорам, указанным в списке C, присваивается значение "открыт" и процессоры из очередей к данным семафорам переводятся в очередь для продолжения их выполнения.
Очередь процессов, конечно, одна, но в ней процессы, "зависшие" на семафорах, соответствующим образом помечаются.
Пусть параллельная программа имеет структуру, представленную на рис. 8.11
информационно-логическим графом (тонкие стрелки — связи по информации, толстые — по управлению).
Обозначение процедуры выше вершины с номером процесса означает, что процесс начинается с нее. Если процедура изображена ниже вершины, значит, процесс заканчивается ее выполнением. Штриховой линией отмечен возможный переход на повторное решение задачи.


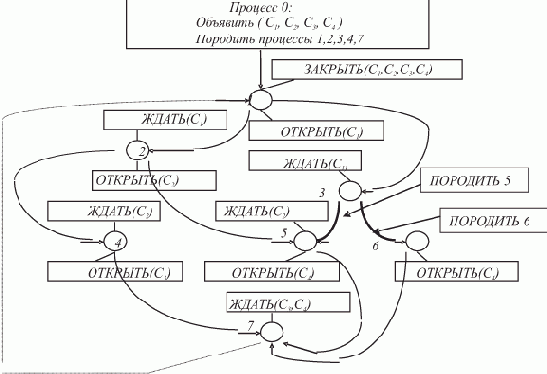
Рис. 8.11.  Синхронизация распараллеливания с помощью семафоров

Выше рассмотрен механизм семафоров для информационно взаимосвязанных или взаимодействующих процессов. Однако семафоры применяются и для синхронизации обращений к общим данным и другим общим ресурсам. Рассмотрим вариант, применяемый в МВК "Эльбрус-2".

Участок программы, использующий (считывающий или модифицирующий) общие для нескольких процессов данные, называется критическим блоком(иногда — критической секцией).

Для синхронизации (соблюдения последовательности) обращения к общим данным семафоры сопровождают массивы данных и указываются в их дескрипторах. В семафоре предусмотрено поле, в котором указано, сколько процессов пользуются в данный момент этим массивом. Очередной процесс перед считыванием из массива увеличивает на единицу значение этого поля, а при выходе из критического блока уменьшает его на единицу. Ненулевое значение поля означает, что семафор "закрыт по считыванию".

Процесс, который должен модифицировать общие данные — этот же массив, — "закрывает семафор по записи", засылая в него соответствующий признак. Попытка закрыть по записи уже закрытый семафор приводит к прерыванию, конфликт разрешает ОС. После модификации общих данных процесс "открывает" семафор.

Таким образом, семафор состоит из двух частей. В одной части содержится счетчик для закрытия по считыванию, в другой — признак (двоичная переменная) для закрытия по записи.

Указанных операций достаточно для решения различных задач синхронизации при использовании общих ресурсов.

Реализация конвейера на симметричной ВС

В СССР существовал опыт построения ВС конвейерного типа на основе систем типа MIMD. Такая система ("Украина"), названная рекурсивной машиной, разрабатывалась под руководством В.М. Глушкова в ИК АН УССР. Этот опыт уже тогда продемонстрировал общность принципа симметричных ВС, хотя направленность разработки на параллельное выполнение циклов типа "пересчет", по нашему мнению, раскрыта не полностью.
Представим себе систему управления в реальном времени, где заявки на обслуживание поступают с максимальной частотой, определяющей минимальную длительность цикла управления (такт) T, по истечении которого на один из объектов должно быть послано управляющее воздействие.
Пусть, однако, длительность решения задач управления одним объектом в несколько раз превосходит значение T, а характер решаемых задач не допускает их распараллеливания.
Тогда единственным способом привлечения многих процессоров для совместного эффективного решения задач, т.е. для организации распараллеливания, является организация обслуживания заявок на конвейере.
Пусть обслуживание одной заявки разбито на n (по числу процессоров) этапов, по возможности — одинаковой длительности. Максимальную из таких длительностей, не превосходящую темпа поступления заявок на обслуживание, примем за такт обслуживания и работы системы. Каждому этапу соответствует программа или программный комплекс. Процессоры ВС специализируются по этапам обслуживания, т.е. каждый из них выполняет какой-то один этап обслуживания заявок.
Свяжем теперь процессоры ВС в один конвейер, на первую станцию которого будем подавать заявки на обслуживание с максимальной частотой, обусловленной тактом, а с последней станции будем снимать результаты обработки информации — с той же частотой (рис. 8.12).

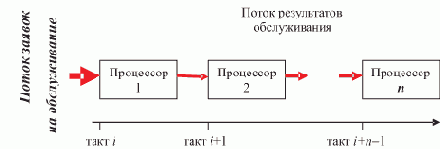
Рис. 8.12.  Организация конвейера

В этом режиме возможны некоторые издержки, связанные с тем, что при постановке задачи организации управляющей системы может возникнуть требование немедленной, не более чем через такт, выдачи результата реакции системы. В данном же случае обработка одной заявки требует n тактов, т.е. задержка составляет n-1 тактов. Но если обработка одной заявки не распараллеливается, то либо нужны кардинальные изменения алгоритмов управления, либо необходимо ждать существенного прогресса в развитии вычислительной техники.
Некоторый выход из положения виден в том случае, когда в рассмотренном режиме производится управление одним объектом. Тогда на основе "физики" процесса может быть справедливым предположение, что каждый результат обработки информации, полученный в i+n-1 -м такте, на основе некоторой пролонгации соответствует данным, как бы полученным не в i-м, а в i+n-2 -м такте. Т.е. необходимо исследовать возможность пролонгации "устаревших" результатов на тот такт, в котором они получены. Такой пролонгацией на последней станции конвейера должен заканчиваться последний этап обработки заявки.

Технология data flow на уровне процедур и процессов в симметричной ВС

"Идеальные" модели data flow (системы, управляемые потоком данных, потоковые ВС) не нашли практического воплощения. Вместе с тем, каждый разработчик, реализовавший при распараллеливании какой-то метод синхронизации частично упорядоченного множества работ, которое представляет собой любая программа или программный комплекс, утверждает, что он создал архитектуру data flow. Это традиционно увеличивает престиж разработки.
Следуя все же изначальной идее, мы под принципом data flow будем понимать такой способ синхронизации параллельного вычислительного процесса, когда отдельные составляющие его работы — программные модули, процессы, процедуры, инструкции, команды — имеют возможность распознавания и заявления о наличии всех данных для своего выполнения. Исполнительные устройства также имеют возможность распознавать работы, для которых существуют все необходимые наборы исходных данных, и выбирать эти работы для выполнения. После выполнения они влияют на состав исходных данных других работ, пополняя их. Все это способствует синхронизированному, осмысленному процессу, максимальной загрузке оборудования, автоматическому использованию всех возможностей реализуемых алгоритмов по распараллеливанию.
Принцип data flow также можно использовать на двух уровнях распараллеливания вычислительного процесса.
Рассмотрим возможность его воплощения на симметричных ВС с помощью механизма синхронизации "почтовых ящиков" (рис. 8.13).

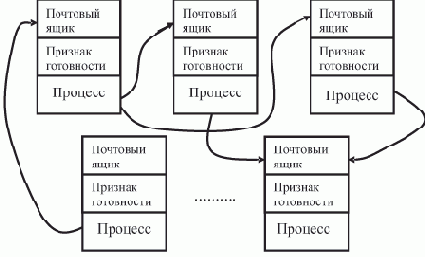
Рис. 8.13.  Схема data flow с помощью "почтовых ящиков"

Процессы могут быть причудливо связаны между собой, обмениваясь через "почтовые ящики". Однако следует не допускать "зацикливания", т.е. информационный граф, соответствующий этой структуре и описывающий частичную упорядоченность работ, не должен содержать контуров.
Итак, мы уже изобразили очередь заданий "к процессору", которая может быть дополнена на основе механизма приоритетов, дополнительными средствами синхронизации с помощью семафоров — для реализации замысла пользователя при построении специализированных систем, а также возможностью "порождать" и "убивать" процессы.
Отметим также, что целесообразно совмещать принцип data flow с принципом децентрализованных ВС. Это вновь оказывается совместимым с основной идеологией семейства "Эльбрус".

Управление процессами в МВК семейства "Эльбрус"

Специально организованная программа, выступающая как самостоятельно, так и во взаимодействии с другими подобными программами, на которые разбита задача, соответствует некоторому процессу. Структуризация программы — разбиение на процессы — может быть предусмотрена заранее, статически. Но возможна и динамическая структуризация. Она основана на том, что процесс может "порождать" другие процессы (процессы-"сыновья") или "убивать" их.
Если выполняемый на процессоре процесс прерывается, то текущее состояние стека процессора, на котором он выполняется, а также состояние некоторых регистров, можно рассматривать, как стек процесса. Он может переходить из активного состояния в пассивное и обратно. Активный стек "наложен" на оборудование и, следовательно, находится в состоянии изменения. Пассивный стек — это "фотография" в области ОП прерванного (или не начавшегося) процесса, ждущего дальнейшего выполнения.
Стек пассивного процесса (рис. 8.10) состоит из шапки и активной области.

Рис. 8.10.  Стек активного процесса

В шапке хранится информация о данном процессе; есть место для хранения содержимого регистров выполнявшего его процессора в момент прерывания для возможности дальнейшего продолжения выполнения процесса. Активная область полностью совпадает с состоянием стека процессора в момент прерывания.
Рассматривая абстрактно стеки процессов, можно говорить о закреплении за ними ресурсов для их активизации. При этом исключается необходимость привязки к конкретным стекам процессоров. Процессоры выступают в роли ресурса для активизации стеков процессов. В этом выражается идея виртуальных процессоров.
Информационной основой работы процессоров МВК является очередь процессов (" к процессору " ), которую составляют указатели на пассивные стеки процессов. Очередь упорядочена по приоритетам. Из очереди процессоры выбирают задания (процессы) по мере окончания выполнения принятых ранее или при их прерывании. В очереди есть и так называемые "ждущие" процессы, которые по мере выполнения условий задержки (например, открытия семафоров) занимают место в соответствии со значением приоритета.
В каждом элементе очереди хранится указатель на следующий элемент, т.е. очередь представляет списковую структуру. Свободный процессор выбирает процесс из "головы" очереди.
ОС может динамически менять приоритеты в режиме мультипрограммного выполнения с разделением времени (в интерактивном режиме). При этом, в частности, реализуется многоочередная дисциплина квантованного обслуживания.
Каждой задаче доступна математическая память размером 232
слов, разбитая на страницы по 512 слов. При выполнении процессов одной задачи в порядке поступления заявок в физической памяти каждой математической странице выделяется сегмент, соответствующий реальному размеру заявки (физических страниц не существует!). При переполнении ОП ОС пересылает часть физических сегментов во внешнюю память (барабаны, диски) и возвращает их по мере необходимости.

Параллельное программирование

Диспетчирование

Диспетчер (рис. 9.3) включается в трех случаях: по признаку "конец задания", по признаку "процессор свободен" и по прерыванию в моменты времени k?, k = 0, 1, ....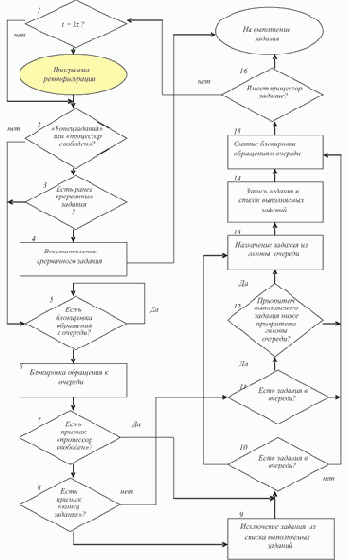

увеличить изображение
Рис. 9.3.  Вычислительный процесс в АСУ коллективного доступа
Признак "конец задания" формируется в случае окончания выполнения каждого из заданий, ранее назначенных на процессор.
Признак "процессор свободен" выдается в случае, когда выполнение программ всех заданий, составляющих один пакет на процессоре, прервано внешним обменом и в соответствии с мультипрограммным режимом целесообразно пополнить пакет из очереди.
При входе в диспетчер проверяется (блок 1) необходимость выполнения программы реконфигурации в момент времени k?, k = 0, 1, .... Затем (блок 2) проверяется, произведено ли включение диспетчера по признакам "конец задания" или "процессор свободен". Если да, то при наличии ранее прерванных заданий (блок 3), обладающих не более высоким приоритетом, чем приоритет прерванного обменом или выполненного задания, производится восстановление первого из таких заданий (блок 4). Если ранее прерванных заданий нет, необходимо обращение к очереди заданий.
Одновременно возможно обращение к очереди только одного процессора, поэтому при каждом обращении проверяется (блок 5), произведена ли блокировка обращения к очереди в результате выполнения диспетчера на другом процессоре. Если такая блокировка установлена некоторым процессором, на котором диспетчер производит аналогичные работы, то диспетчер на данном процессоре пребывает в режиме ожидания, циклически выполняя блок 5. При отсутствии блокировки она устанавливается (блок 6).
Если включение диспетчера произошло по признаку "процессор свободен" (блок 7), то при наличии заданий в очереди (блок 10) производится назначение на процессор задания, составляющего голову очереди (блок 13). Если включение диспетчера произошло по признаку "конец задания" (блок 8), то выполненное задание исключается из списка выполняемых данным процессором заданий (блок 9). Далее также производится назначение нового задания (блок 13) при наличии заданий в очереди (блок 10).
Если в результате выполнения блоков 7 и 8 оказалось, что диспетчер включен в момент времени k?, k = 0, 1, ..., при наличии заданий в очереди (блок 11) проверяется (блок 12), является ли приоритет выполняемого на процессоре задания ниже приоритета задания, составляющего голову очереди. Если является, то для дальнейшего выполнения выбирается задание, составляющее голову очереди.
Выбранное задание отмечается в списке выполняемых заданий (блок 14). Снимается блокировка обращения к очереди (блок 15), и, если в результате работы диспетчера процессор обладает готовым к выполнению заданием (блок 16), осуществляется переход к его выполнению. В противном случае продолжается циклическое обращение к диспетчеру до формирования готовых к выполнению заданий.

Схема организации параллельного процесса

Объединим в законченную модель методы управления, диспетчирования, синхронизации работ и контроля состояния вычислительных средств при построении схемы АСУ коллективного пользования на основе многопроцессорной ВС, ВК или процессоров локальной сети, располагающих общей памятью или достаточно оперативным обменом.
Считаем, что в состав технических средств АСУ входит множество терминальных устройств или периферийных процессоров локальной сети, с помощью которых в ВС поступают заявки на решение одной или более задач. Кроме того, в ВС могут решаться фоновые задачи, связанные с наступлением предусмотренных сроков их решения.
Каждая заявка проходит следующие этапы обработки (рис. 9.1): прием текста заявки в приемное поле (область памяти ВС), связанное с терминалом; дешифрация и присвоение приоритета; формирование задания в списке заданий ВС; выполнение, выдача в ответное поле результатов в стандартной форме; выдача ответа на терминальное устройство.

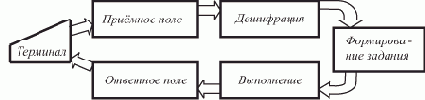
Рис. 9.1.  Этапы обработки заявок

На рис. 9.2 показано закрепление средств специального программного обеспечения за процессорами ВС.

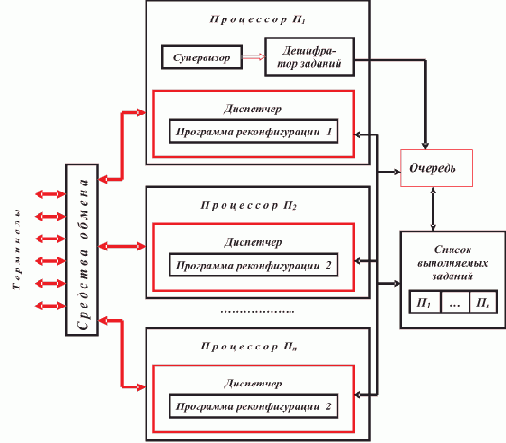
Рис. 9.2.  Организация вычислительного процесса и средств повышения надёжности
Выбором головного процессора П1 и установлением нумерации Пi, i = 2 , ... , n остальных ведомых процессоров определяется конфигурация ВС. Функции головного может исполнять любой из процессоров в результате реконфигурации ВС. Реконфигурация осуществляется по признаку, вырабатываемому в ВС в случае изменения ее состава. Смена головного процессора производится при его отключении.
На головном процессоре выполняются супервизор ВС и дешифратор заданий. В памяти, доступной всем процессорам, хранится очередь заданий, учитывающая их приоритет, а также список заданий, выполняемых каждым процессором. Децентрализованное диспетчирование осуществляется в основном с помощью идентичных экземпляров диспетчеров, выполняемых каждым процессором, в том числе и головным. Диспетчеры отличаются входящими в их состав программами реконфигурации: для головного процессора (программа реконфигурации 1) и для ведомых (программа реконфигурации 2).

Супервизор включается по прерыванию в моменты времени k?, k = 0, 1, ... . В эти моменты производится блокировка прерывания процессора П1

работами с более низким приоритетом. Супервизор имеет высший приоритет по отношению ко всем работам в АСУ, уступающий лишь основным работам операционной системы общего программного обеспечения ВС.

Затем включается программа реконфигурации ВС, которая после выполнения всех необходимых работ, предусмотренных для головного процессора, вновь передает управление супервизору ВС.

Начинается циклический опрос состояния буферов терминалов. Каждый буфер терминала представляет собой область памяти, в которой накапливается информация, поступающая от закрепленного за ней терминального устройства через канал связи. Если очередной проверяемый буфер не пуст, проверяется, верен ли пароль, представляющий собой код или слово, закрепленное за каждым терминальным устройством или пользователем, с целью ограничения доступа к АСУ. Верное значение пароля является признаком начала текста входного сообщения. Проверяется, заканчивается ли текст признаком "конец задания", указывающим на окончание выдачи входного сообщения. Если выдача задания еще не закончена, увеличивается значение счетчика времени существования незаконченных заданий от данного терминала. Счетчик позволяет выявлять случаи, когда выдача заданий по какой-либо причине оказывается прерванной. По достижении максимального значения этого счетчика буфер терминала чистится.

Если выдача задания закончена, супервизор передает управление дешифратору заданий, который на основе входного сообщения формирует задание. Заданию присваивается значение приоритета на основе таблицы приоритетов. Сформированное задание оформляется как процесс или несколько взаимосвязанных процессов и помещается в очередь заданий в соответствии со значением приоритета. Указанная работа производится для всех буферов терминалов.

После формирования заданий по входным сообщениям с терминалов супервизор приступает к подготовке выполнения периодических заданий, предусмотренных регламентом обновления информации о состоянии средств системы.


Для каждого задания, включенного в список выполняемых периодически с заданным темпом решения, проверяется, совпадает ли значение k? с началом его выполнения. Если совпадает, в очередь заданий заносится соответствующее задание с указанием его приоритета. Рассчитывается следующий момент начала выполнения данного задания.

Этим заканчиваются все работы супервизора. Снимается ранее установленная блокировка прерывания от менее приоритетных задач, после чего управление передается диспетчеру.

Программа реконфигурации для головного процессора в стандартной ситуации получает управление от супервизора. Через блок внешних сигналов связей или общую память на все процессоры в специально организованные области памяти рассылается текущее значение таймера. В свою очередь, в память П1 также поступают отметки времени от остальных активных процессоров, вытесняя пришедшие ранее. Каждая из этих отметок сравнивается с текущим значением t таймера П1. Если значение отметки, пришедшей от процессора Пi, превышает значение t - 2?, процессор Пi признается активным. Отрезок времени длиной 2? принимается во избежание дополнительной синхронизации обмена отметками. Если последняя отметка от процессора Пi пришла ранее момента t - 2?, этот процессор считается вышедшим из активного состояния. Задания, выполнение которых начато, но не закончено на Пi, переводятся вновь в очередь заданий. Для этого используется список выполняемых заданий. Производится перенумерация процессоров Пj для j > i уменьшением их номера на единицу. Таким образом производится анализ временных отметок всех ведомых процессоров. По окончании анализа управление вновь передается супервизору.

Второй вход в программу реконфигурации для головного процессора осуществляется только в момент возложения на данный процессор функции головного в результате реконфигурации и производится в обход блока отметки данного процессора в областях памяти других процессоров. Причина в том, что данный процессор, выполняя функции ведомого, перед указанным входом такую рассылку временной отметки уже произвел.

Программа реконфигурации для ведомого процессора (программа реконфигурации 2) входит в состав диспетчера и включается по прерыванию в моменты времени k?, k = 0, 1, .... Устанавливается блокировка прерывания от работ с более низким приоритетом, т.е. от всех работ АСУ. Рассылается временная отметка всем процессорам с номерами, большими номера данного процессора. Производится анализ, отметился ли в области памяти данного процессора хотя бы один процессор с меньшим номером. Если отметился, уточняется номер данного процессора с помощью числа активных процессоров с меньшими номерами, после чего снимается установленная ранее блокировка прерывания и включается диспетчер.

Если данный процессор не обнаружил временных отметок всех процессоров с меньшими номерами, он считывает все элементы специального программного обеспечения, превращающие его в головной. Продолжается выполнение программы реконфигурации для головного процессора со второго входа, как говорилось выше.

Параллельное программирование

Частичная упорядоченность работ отсутствует

Пусть на ВК или многопроцессорную ВС поступает поток заданий, которые объединяются в пакет. Каждое задание требует запуска соответствующей программы. Программы не зависят друг от друга, т.е. одни программы не используют результаты выполнения других в качестве исходных данных. Сформированный пакет заданий необходимо выполнить за минимальное время, добившись максимальной эффективности вычислительных средств. Это означает необходимость распределения работ по времени их выполнения "поровну" между процессорами ВС.
Данная задача известна как задача о рюкзаках и отображает необходимость распределения неделимых объектов (нельзя разрезать консервную банку или спальный мешок!) так, чтобы веса рюкзаков были как можно ближе к одинаковым.
Известен "хороший" эвристический алгоритм, для которого не удалось найти пример неточного оптимального распределения.
Формируется очередь заданий (программ), представляющая собой невозрастающую последовательность времен их выполнения. Например, такая очередь может иметь вид, представленный на рис. 10.1, где длина каждого прямоугольника условно соответствует времени выполнения программы, указанного внутри него.

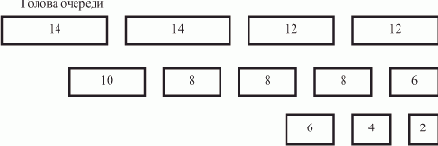
Рис. 10.1.  Множество работ, упорядоченное по невозрастанию времени выполнения
Сформулируем основное правило назначения: исполнитель, набравший минимальный вес, берет работу из головы очереди.
Пусть заданы три процессора-исполнителя. Первоначально все исполнители свободны. Тогда их приоритет обращения к очереди определяется их номерами. Очевидно, что при трехкратном обращении к очереди (каждым процессором) их загрузка будет выглядеть, как показано на рис. 10.2.

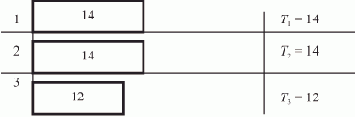
Рис. 10.2.  Первый шаг распределения
Справа на рисунке показана суммарная текущая загрузка каждого исполнителя.
2. Так как теперь минимально загружен третий процессор, он выбирает работу с весом 12, и вся картина загрузки принимает вид, отраженный на рис. 10.3.

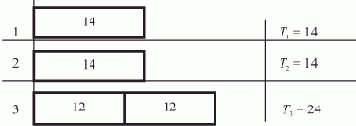
Рис. 10.3.  Второй шаг распределения
3. Затем последовательно назначаются на процессоры 1 и 2 работы с весами 10 и 8. Загрузка процессоров принимает вид, показанный на рис. 10.4.

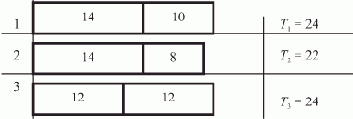
Рис. 10.4.  Третий шаг распределения
4. Продолжая таким же образом, получим окончательный план (рис. 10.5) выполнения работ.

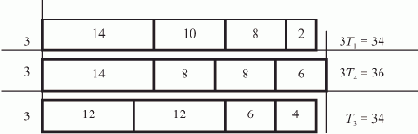
Рис. 10.5.  Окончательный план выполнения работ
Легко убедиться в том, что более "короткого" плана выполнения данного комплекса работ нет, т.е. распределение совпало с оптимальным.

Диспетчер последовательного назначения для неоднородной ВС

В основе диспетчера лежит следующее решающее правило:
При известных текущих значениях занятости процессоров, готовые к выполнению работы назначаются так, чтобы в первую очередь выполнялись более трудоемкие, и чтобы каждая работа была назначена на тот процессор, который раньше других закончит ее выполнение.
Введем сквозную нумерацию процессоров от 1 до . Зададим вес {tj1 ... tjN} j-й вершины (j = 1 ... m; m — размер матрицы S или объем буфера диспетчера) так, что при новой нумерации процессоров tjl — время выполнения j-й работы l-м процессором. Например, при k = 2, n1 = 1, n2 = 2 расширенная матрица следования на рис. 10.15б примет вид, представленный на рис. 10.16.
В процессе распределения работ будем формировать расписание в виде таблицы ?, состоящей из N строк, каждая из которых соответствует одному процессору. В строке будем записывать последовательность заданий одному процессору. Задания имеют два вида: выполнить работу , простоять t единиц времени (изображается ). Момент Ti , i = 1 ... N, окончания (отсчет ведется от нуля) выполнения последней работы или простоя, назначенных к данному моменту распределения i-му процессору, назовем текущим временем занятости процессора.
В процессе распределения и имитации выполнения работ будем использовать множество A номеров работ, уже назначенных на процессоры, но не выполненных в анализируемый момент времени. A представляет собой таблицу, содержащую пары "назначенная для выполнения задача — время окончания ее выполнения ", т.е. A = {j - tj}.
Множество R — множество работ, соответствующих не назначенным входам (нулевым строкам) текущего значения изменяемой матрицы следования S.
Алгоритм диспетчера

Полагаем первоначально Tl = 0, l = 1, ... N, A = B = R = , ? = 1, S? = S, (? — номер шага распределения). Переходим к выполнению 5.

Находим в множестве A значение tmu = minj
{ti} и множество B A номеров работ, назначенных на процессоры и закончивших выполнение к моменту t?. Полагаем равными нулю все позиции A, составляющие B.
Этим имитируется окончание выполнения работ на процессорах к моменту времени t?.

Для всех процессоров, для которых текущее время занятости меньше значения t? (Ti < t?), записываем простой в течение времени t? - Ti (символом простоя ). Для этих процессоров полагаем Ti = t?.

Исключаем из S? строки и столбцы, соответствующие всем работам из B, после чего матрицу S? (S*?) уплотним. Полагаем ? := ? + 1. Таким образом сформируется матрица S? (а также S*?) на новом шаге распределения.

Находим множество R — входов матрицы следования S?, соответствующих не назначенным ранее работам. Если R , переходим к выполнению 6, в противном случае выполняем пункт 2.

Пусть для определенности R = {1 ... r}, работе p соответствует вес {tp1 ... tpN}, p = 1 ... r. Формируем суммы Tl + tpl , l = 1 ... N, p = 1 ... r. Для каждого значения p (т.е. для каждой работы из R) находим минимальную (по l) из таких сумм, т.е. для каждой работы находим один или несколько процессоров, на которых время окончания выполнения этой работы минимально при текущих значениях занятости процессоров. Найденные суммы сведем в невозрастающую последовательность R*, состоящую из r чисел. При этом сохраним информацию о соответствии процессорам.

Ставим в соответствие каждой p-й работе, представленной в последовательности R*, значение ?p, равное числу процессоров, при выполнении на которых достигается найденное минимальное время окончания выполнения этой работы.

Производим последовательное назначение работ на процессоры следующим образом. Назначаем не более N работ слева направо в соответствии с вхождением времени окончания их выполнения в последовательность R*. Каждую p-ю работу назначаем на все те процессоры, (их число равно ?p), на которых достигается входящее в R* время окончания выполнения. В результате те работы, для которых ? > 1, окажутся назначенными более чем на один процессор, а на один процессор на данном шаге могут оказаться назначенными более одной работы. Чтобы определить окончательно, на какой процессор должна быть назначена p-я работа, воспользуемся следующей процедурой.


Для каждого процессора проводим анализ, сколько работ назначено на него на данном шаге распределения. Если назначения не произошло, переходим к анализу назначения на следующий процессор или заканчиваем анализ процессоров, если все они просмотрены. Если оказалась назначенной на процессор одна, p-я, работа, считаем ее окончательно закрепленной за данным процессором, и, если ?p > 1, исключаем ее из рассмотрения при анализе последующих процессоров — т.е., снимаем ее с назначения на другие процессоры. Если на процессор назначено более одной работы, закрепляем за процессором лишь ту работу p, которая имеет минимальное значение ?p. Если несколько работ имеют равное минимальное значение ?p, назначаем любую (первую) из них. Для множества работ {?}, отклоненных от назначения на данный процессор, полагаем ?? := ??

- 1. Значение ?? = 0 означает, что работе ? отказано в назначении на данном шаге распределения. Назначенную работу исключаем из рассмотрения при анализе следующих процессоров. Номера назначенных работ оказываются записанными в строки таблицы ?, соответствующие процессорам. Эти номера исключаем из R. Номер каждой назначенной работы и время окончания ее выполнения (оно же — время занятости процессора) заносим в A.

Проверяем, все ли работы распределены. При отрицательном результате проверки переходим к выполнению 2.

Конец алгоритма.

Пример.

При k = 2, n1 = 1, n2 = 2, (N = 3) распределим работы, отображенные расширенной матрицей следования на рис. 10.16 (соответствующей графу на рис. 10.15), для минимизации времени выполнения.


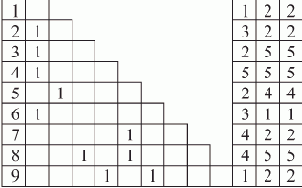
Рис. 10.16.  Преобразование расширенной матрицы следования

T1 = T2 = T3 = 0, A = B = , S1 = S, R = {1}. Выполнение работы 1 ранее всех закончит процессор 1. После ее назначения T1 = 1, T2 = T3 = 0, A = {1 - 1}.

Найдем в A работу 1 с минимальным временем окончания выполнения, равным 1. Записываем простои в одну единицу времени процессорам 2 и 3. Таблица ? принимает вид

После исключения первой строки и первого столбца из S1 (т.е.


по матрице S2) найдем R = {2, 3, 4, 6}. Составим таблицу 10. 1 времени окончания выполнения каждой работы из R каждым процессором l = 1, 2, 3. Минимальное время окончания выполнения каждой работы выделено.

Таблица 10.1. l Tl+t2l Tl+t3l Tl+t4l Tl+t6l

1	4	3	6	4
2	3	6	6	2
3	3	6	6	2

Формируем последовательность R* = {6 (4; 1, 2, 3, ?4 = 3), 3 (2; 2,3, ?2 = 2), 3( 3; 1, ?3 = 1), 2 (6; 2,3, ?6 = 2)}, где в круглых скобках указаны номер работы, список процессоров, на которых достигается минимальное время окончания ее выполнения, и число ?p

этих процессоров.

Назначим первоначально (таблица 10.2) работу 4 на процессоры 1, 2, 3, работу 2 — на процессоры 2 и 3 , работу 3 — на процессор 1.

Таблица 10.2.

1	4 (?4 = 3), 3(?3 = 1)
2	4 (?4 = 3), 2(?2 = 2)
3	4 (?4 = 3), 2(?2 = 2)

После анализа значений ?p оставим на процессоре 1 работу 3 (после чего ?4 = 2), на процессоре 2 — работу 4 (после чего ?2 = 1), на процессоре 3 — работу 2, A = \{3 - 3, 4 - 6, 2 - 3\}. Таблица распределения ? примет вид

B = {2, 3}. После исключения строк и столбцов, соответствующих работам 2 и 3, из матрицы S2, т.е. по сформированной матрице S3, найдем R = {5, 6}. Составим таблица 10.3 значений времени окончания выполнения каждой работы из R каждым процессором.

Таблица 10.3. l Tl+t5l Tl+t6l

1	5	6
2	10	7
3	7	4

Из таблицы найдем R* = {5 (5; 1, ?5 = 1), 4 (6; 3, ?6 = 1)},

Назначим работу 5 на процессор 1, работу 6 — на процессор 3, A = {5 - 5,4 - 6, 6 - 4}. Таблица распределения ? примет вид

B = {6}. После исключения строки и столбца, соответствующих работе 6, из матрицы следования S3, т.е. по сформированной матрице S4, найдем R = . Назначим процессору 3 простой в течение одной условной единицы времени. Таблица ? примет вид

B = {5}. После преобразования матрицы S4, т.е. по матрице S5, найдем R = {7, 8}. Из таблицы 10.4, аналогичной таблице 3, найдем R* = {9 (8;1, ?8 = 1), 7 (7; 3, ?7 = 1)} .

Таблица 10.4. l Tl+t7l Tl+t8l

1	9	9
2	8	11
3	7	10

Назначаем работу 8 на процессор 1, работу 7 — на процессор 3. Таблица ? примет вид

B = {4}. После исключения строки и столбца, соответствующих работе 4, из матрицы следования S5, т.е. по сформированной при этом матрице S6, найдем R = {9}. Время окончания выполнения работы 9 на процессорах равно соответственно 10, 8, 9. Назначаем работу 9 на процессор 2. Таблица ? примет окончательный вид

Дополнение.

Данный диспетчер для неоднородной ВС построен на основе обобщения рассмотренного диспетчера последовательного назначения для однородных ВС, который можно рассматривать как частный случай при k = 1.

Он применим и в другом частном случае: когда отсутствует частичная упорядоченность работ, то есть когда надо разделить "поровну" взаимно независимые работы между n исполнителями. Наглядный пример такого распределения составляет задача о рюкзаках, рассмотренная в разделе 10.1.1.

Диспетчер распределения частично упорядоченного множества работ в однородной ВС

В основе практических диспетчеров ВС лежат эвристические алгоритмы оптимального распараллеливания. Это обусловлено высокой сложностью методов точного решения задач распараллеливания. Реализация таких методов потребовала бы неоправданно больших затрат времени компьютера. Кроме того, подобные методы не позволяют получить гарантированные оценки времени решения: это время колеблется в большом диапазоне в зависимости от случайно складывающейся ситуации. Эвристические методы обеспечивают компромисс между временем работы диспетчера и точностью вырабатываемого расписания работы процессоров ВС.
Частичная упорядоченность заданий, точнее — программ их выполнения, означает, что одни программы используют результаты выполнения некоторых других программ данного пакета. Отражая этот факт графически и введя нумерацию программ, получают графовую структуру, показанную, например, на рис. 10.6.

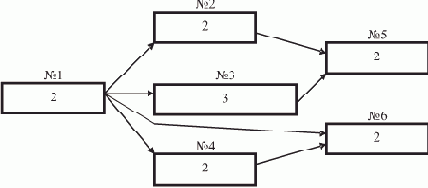
Рис. 10.6.  Частично упорядоченное множество работ
Априорное формирование очереди невозможно, и очередность назначения работ выявляется динамически, по мере выполнения или имитации выполнения предыдущих шагов распределения заданий.
Пусть программы, образующие данную структуру, необходимо распределить между двумя процессорами так, чтобы время их совокупного выполнения — время окончания выполнения вычислительного процесса, было минимальным.

Выделяются входы графовой структуры, т.е. программы, не использующие выходную информацию других программ. В данном случае это — единственная программа № 1. Она назначается на первый свободный процессор 1. Множество входов исчерпано. Временная диаграмма загрузки процессоров ВС принимает вид, показанный на рис. 10.7.

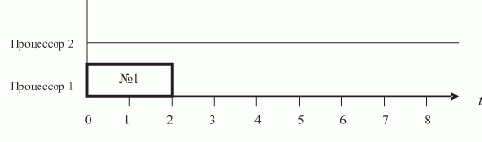
Рис. 10.7.  Первый шаг распределени

Имитируется счет времени t, чем отслеживается состояние системы. Видно, что только в момент t = 2, т.е. после окончания выполнения программы № 1, могут появиться возможности для дальнейшего назначения. Работу №1 необходимо исключить из рассмотрения. Граф-схема на момент t = 2 принимает вид, показанный на рис. 10.8.


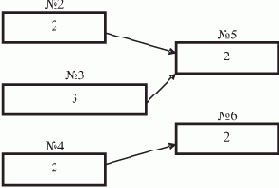
Рис. 10.8.  Имитация выполнения первой работы

Вновь выделяются входы графовой структуры текущего вида. В данном примере это программы, составляющие множество {№ 2, № 3, № 4}.

Здесь целесообразно ввести в действие обязательный элемент любого эвристического, т.е. использующего основополагающую догадку, алгоритма решения сложной комбинаторной задачи, к которой относится задача диспетчирования, — решающее правило:

Из тех задач, выполнение которых может быть начато на данном шаге распределения, в первую очередь назначать ту, которая обладает максимальным временем выполнения.

Частным случаем этого правила является способ назначения заданий при отсутствии частичной упорядоченности.

В результате упорядочения программ по невозрастанию времен их выполнения формируется очередь на данном шаге распределения:{ № 3, № 2, № 4}. Диаграмма последовательной однократной загрузки свободных с момента t = 2 процессоров принимает вид, показанный на рис. 10.9.


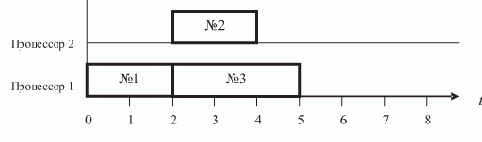
Рис. 10.9.  Второй шаг распределения

Вновь включается счетчик времени, следя за состоянием системы. Очевидно, что какие-то изменения могут наступить только в результате выполнения заданий. В момент t = 4 заканчивается выполнение программы № 2. Хотя новых входов в граф-схеме не образуется, есть вход (программа № 4), оставшийся после предыдущего шага распределения. Программа № 4 назначается на освободившийся процессор 2.

Затем таким же образом производится назначение программ № 5 и № 6, и формируется окончательный вид (рис. 10.10) временной диаграммы выполнения пакета заданий.


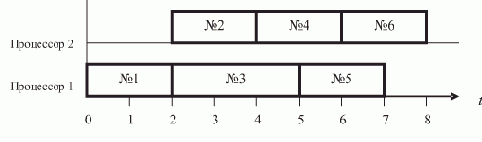
Рис. 10.10.  Окончательный план выполнения работ

Значит, весь пакет программ выполняется за восемь условных единиц времени. Полученный план выполнения заданий в примере совпадает с оптимальным, т.к. более "короткого" расписания найти невозможно. В общем случае это свидетельствует о том, что данный алгоритм диспетчера "хороший", но не обеспечивает точного решения задачи оптимального распараллеливания.Точное же решение такой задачи, ввиду ее высокой сложности, не может служить основой оперативного диспетчера ВС.

Формальное описание алгоритма диспетчера

Пусть задана (рис. 10.11) расширенная матрица следования S*, отражающая информационные связи внутри множества m работ j = 1...m. Веса tj — времена выполнения каждой j-й работы на каждом из n процессоров однородной ВС с общей ОП.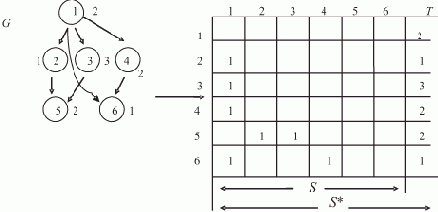

Рис. 10.11.  Граф алгоритма и расширенная матрица следования
Необходимо составить расписание параллельного выполнения работ, при котором время выполнения всей совокупности работ минимально.
Вспомогательные построения
Пусть в результате распределения составляется таблица-расписание?, содержащая n строк — расписаний одному процессору. В строке — последовательность заданий двух видов: выполнить работу (задачу, оператор и т.д.) , простоять t единиц времени (). Момент Ti, i = 1 ... n, окончания (отсчет — от нуля) выполнения последней работы или проcтоя, назначенных к данному шагу распределения i-му процессору, назовем текущим временем занятости процессора.
Пусть в процессе распределения формируется таблица (множество) A номеров задач, назначенных к данному шагу распределения последними для выполнения на каждом процессоре. Эти номера заносятся в позиции, закрепленные за каждым процессором. Если последним был записан простой, в соответствующей позиции значится 0.
В множество B будем объединять процессоры (один или более), имеющие на данном шаге распределения минимальное время занятости.
В множество ? выделим те работы из A, которые выполняются на процессорах из B.
Множество R — множество работ, соответствующих входам (нулевым строкам) текущего значения изменяемой в процессе распределения матрицы следования S.
Алгоритм.

Полагаем первоначально Ti = 0, i = 1 ... n, A = {0, ...,0}, B = {1 ... n}, = , R = , ? = 1, S?* = S*; переходим к выполнению шага 6.

Находим Tmu = min{Ti} и множество B номеров процессоров с найденным временем занятости.

Находим множество ? A номеров задач, назначенных последними на процессоры из B. После построения ? все позиции в A, соответствующие процессорам из B, полагаем равными нулю. Этим моделируется окончание выполнения задач на данных процессорах к моменту T?.

Если ? = , переходим к выполнению шага 7 при R и шага 10 при R = ; при ? выполняем следующий шаг.

Исключаем из S?* строки и столбцы, соответствующие задачам, составляющим множество ?.
Полагаем ? := ? + 1.

Находим множество R входов матрицы следования S?, соответствующих не назначенным ранее задачам. Если R = , переходим к выполнению шага 10.

Располагаем номера задач, составляющих R, в порядке невозрастания времени их выполнения.

Производим поочередное назначение задач, составляющих упорядоченное множество R, на процессоры, составляющие множество B. Назначенные задачи исключаем из R, а процессоры, на которые произведено назначение, — из B. Номер каждой назначенной задачи заносим в позицию A, соответствующую данному процессору. Время занятости этого процессора увеличиваем на время выполнения назначенной задачи. Последовательное назначение прекращается в одном из трех случаев: a) R

, B = ; б) R = , B = ; в) R = , B .

Примечание. Шаги 7 и 8 реализуют решающее правило, лежащее в основе данного (и каждого!) эвристического (практичного, эффективного, но не основанного на точном решении сложной задачи) алгоритма распараллеливания. Повторим его:

Из тех задач, выполнение которых может быть начато на данном шаге распределения, в первую очередь назначать ту, которая обладает максимальным временем выполнения.

Возможны и другие решающие правила, например, основанные на допустимом резерве времени до обязательного момента окончания решения и др. Применяемое здесь решающее правило обеспечивает высокое быстродействие диспетчера и достаточно редкое (менее 10 %) отклонение результатов распределения от тех же результатов, получаемых методом точного решения задачи распараллеливания.

Если в результате выполнения шага 8,B = , переходим к выполнению шага 12.

Если B , (при этом R = ), находим T? — значение времени занятости одного из процессоров, минимально превосходящее T?.

В множество строк, соответствующих множеству B процессоров с временем занятости T?, записывается задание — простой ; для всех процессоров из B время занятости полагается равным T?.

Проверяем, все ли задачи распределены: S?* =


? При отрицательном результате проверки выполнение алгоритма продолжаем с шага 2.

Пример. Продолжим рассмотрение G и S* (S), представленных на рис. 10.11.

R = {1}, T1 = T2 = 0, A = {0, 0}, B = {1, 2}, ? = , ? = . Задачу 1 назначаем на первый процессор и исключаем из R. После этого A = {1, 0}, B = {2}, T1 = 2. Т.к. теперь R = , B , записываем во вторую строку ? "простой в 2 единицы". Таблица ? примет вид

A = {1, 0} , T? = T1 = T2 = 2 , B = {1, 2} , ? = {1}. После исключения из S* первой строки и первого столбца (рис. 10.12) сформируем множество входов R = {2, 3, 4} которое переупорядочим по невозрастанию времен решения задач, R = {3, 4, 2}.


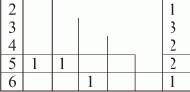
Рис. 10.12.  Матрица следования после первого шага распределения

В результате последовательного назначения задач из R таблица ? примет вид

A = {3, 4}, T? = min {5, 4} = 4, B = {2}, ? = {4}. После исключения из S* (рис. 10.13) информации о задаче 4 сформируем множество неотмеченных в A входов R = {2, 6}.


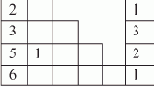
Рис. 10.13.  Матрица следования после второго шага распределения

Таблица ? примет вид

A = {3, 2} , T? = 5 , B = {1, 2}, ? = {3, 2}. После исключения (рис. 10.14) информации о задачах 3 и 2 из S* найдем R = {5, 6}. В результате последовательного назначения получаем окончательный вид таблицы ?.


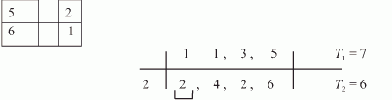
Рис. 10.14.  Матрица следования после третьего шага распределения и окончательный план выполнения работ

Tреш = max{T1, T2} = 7 и совпадает с точным минимальным.

Информационные графы с векторными весами вершин

Часто в состав ВС включают средства (процессоры) разной специализации и производительности. Например, МВК может комплексироваться разными ЭВМ, но допустимо исследование его как единой ВС. Новые ВС могут дополняться процессорами — эмуляторами ранее распространенных ЭВМ — для использования ранее разработанных программных продуктов. ВС, используемые в системах управления, дополняются процессорами, специализированных для решения конкретных задач, и т.д.
Появляется дополнительный выбор: на процессор какого типа возложить решение задачи? На основе каких типов процессоров с учетом количества процессоров разного типа целесообразно скомпоновать систему? Как спланировать работу неоднородной ВС таким образом, чтобы данный алгоритм выполнялся за минимальное время?
Пусть ВС комплектуется процессорами k типов по производительности и специализации. Пусть ni , i = 1 ... k, — число процессоров i-го типа. Тогда для каждой работы следует задавать не скалярный вес (такими весами мы пользовались ранее), а вектор — вес. Каждая компонента такого веса равна времени выполнения работы процессорами соответствующего типа. Например, для k = 2 граф G с векторными весами вершин представлен на рис. 10.15а, а расширенная матрица следования — на рис. 10.15б.

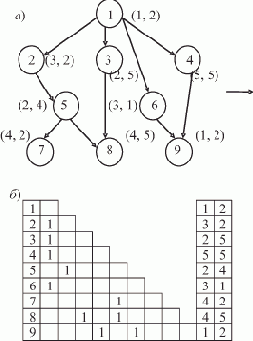
Рис. 10.15.  К распределению работ в неоднородной ВС: а — информационный граф, б — расширенная матрица следования
На таком графе можно сформулировать оптимизационные задачи 1 и 2 (см. лекцию 20). Однако их методы решения весьма трудоемки (задачи экспоненциальной сложности), поэтому их заменяют эвристическими методами (полиномиальной сложности). Более того, пусть мы умеем решать задачу нахождения плана выполнения работ, минимизирующего время выполнения всего алгоритма (т.е. задачу 2). Тогда на основе этого решения можно давать заключение о возможности применения ВС в каждой конкретной комплектации, т.е. о решении задачи 1. При этом придется испытывать различные комбинации такой комплектации.
Таким образом, необходимо построить достаточно эффективный алгоритм диспетчирования неоднородной ВС, т.е. эвристический алгоритм планирования выполнения за минимальное время алгоритма, заданного информационным графом с векторными весами вершин.

Параллельное программирование

Основные понятия

Объектами распараллеливания являются неделимые процессы — работы, на которые разбивается исходный алгоритм или разрабатываемая программная система.
Процессы используют различные устройства, данные, компоненты программного обеспечения, которые называются ресурсами системы.
Ресурсы, используемые несколькими процессами, называются разделяемыми.
Разделяемые ресурсы, которые одновременно могут использоваться не более чем одним процессом, называются критическими ресурсами. (Например, очередь "к процессору" — критический ресурс.)
Участки программы (процесса), где процессы обращаются к разделяемому ресурсу, называются критическими интервалами (блоками, секциями).
Процессы называются взаимосвязанными, если они используют общие критические ресурсы.
Процессы называются информационно-взаимосвязанными, если они обмениваются информацией. Процессы называются взаимосвязанными по управлению, если один из них вырабатывает условия для активизации другого (других). Ограничения на порядок выполнения процессов называются синхронизацией процессов. Отношения между процессами задаются правилами синхронизации. Для задания правил синхронизации используются механизмы (средства) синхронизации (рассмотренные выше матрицы следования, семафоры и др.) Задача синхронизации — это задача, в рамках которой требуется согласовать выполнение нескольких процессов. Решение таких задач достигается с помощью механизмов синхронизации. С задачами синхронизации связывают тупики (тупиковые ситуации). Тупик — это взаимная блокировка процессами друг друга, при которой их выполнение не может быть продолжено, а также самоблокировка.
Например, процессу A необходимы внешние устройства X, Y. С устройством Y пока работает процесс B. Тогда процесс A "захватывает" пока устройство X и ждет освобождения Y. Но устройство X потребовалось и процессу B, который также "зависает" в ожидании его освобождения.
Под общим тупиком подразумевается взаимная блокировка всех взаимосвязанных процессов. Под локальным тупиком понимается бесконечная блокировка одного из процессов при попытке войти в критический интервал.
Выше был приведен пример:

"Закрыть адрес по считыванию" a

"Считать по адресу" а

Здесь возможен локальный тупик — бесконечное выполнение команды (2), если другой процесс (на другом процессоре) или ОС не "откроет" адрес а.

Средства синхронизации параллельных процессов

1. Матрица следования. Является эффективным средством синхронизации при реализации первого способа распараллеливания. Допускает автоматическое составление в процессе диспетчирования, как рассмотрено ранее. Легко составляется пользователем, планирующим параллельный процесс. Для оптимального планирования требует временной оценки работ либо оценки их сравнительной трудоемкости.
Например, пусть методом "разделяй и властвуй" производится распараллеливание сортировки слиянием. Известны оценки сложности такой сортировки (как функции параметра n — длины последовательности).
При разбиении последовательности на две можно построить граф G и его матрицу следования S (рис. 11.1).

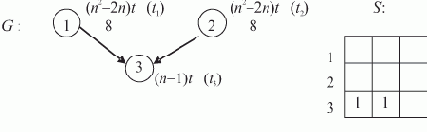
Рис. 11.1.  Составление взвешенного информационного графа и матрицы следования
Здесь t — время совместного анализа двух элементов последовательности. Значит, веса вершин t1, t2, t3 определены при заданных n и t.
2. Механизм семафоров.Различают двоичные семафоры, имеющие значения "открыт" и "закрыт", и семафоры-счетчики. "Закрытие" увеличивает их на единицу, "открытие" — уменьшает на единицу.
Анализ задач и, в частности, задач обработки больших массивов данных (баз данных и баз знаний) показал целесообразность совместной реализации этих двух принципов в многопроцессорной вычислительной системе. В одном семафоре, назовем его комбинированным, в действительности воплощены два семафора: двоичный и счетчик:


В начале считывания из массива выполняется операция Сб := Сб+ 1; при окончании считывания — операция Сб := Сб - 1. Значение Сб 0 означает: семафор C "закрыт по считыванию".
При записи в массив выполняется операция: Са := 1, "закрыть", т.е. семафор C "закрывается по записи". При окончании записи выполняется операция Cа := 0 — "открыть", т.е. семафор C "открывается по записи".
Однако удобства семафора-счетчика могут быть реализованы в процедурах над двоичными семафорами.
Выполнение этих процессов на процессорах будет продолжено с повторного выполнения тех процедур ЗАКРЫТЬ (C') или ЖДАТЬ (C''), на которых ранее произошло прерывание данной задачи. Таким образом, если прерывание произошло при выполнении процедуры ЗАКРЫТЬ (C'), то всем семафорам, указанным в списке C', вновь присваивается значение "закрыт". При этом, если среди множества семафоров C' C окажутся такие, которые ранее были закрыты, или другой процесс (на другом процессоре) успел закрыть семафор из C' раньше, то выполнение данного процесса вновь прервется и он станет в очередь к закрытым семафорам.

Процедура ПРОПУСТИТЬ (С) полностью соответствует упрощенной версии процедуры ОТКРЫТЬ (C). Семафорам, перечисленным в списке C, присваивается значение "открыт", и процессы из очередей к данным семафорам переводятся в очередь "к процессору". Если процессы находились в очереди к семафорам из С после прерывания в результате выполнения процедур ЗАКРЫТЬ или ЖДАТЬ, то повторного выполнения этих процедур не происходит; процессы выполняются со следующей инструкции.

Пример.

Пусть в однопроцессорной ВС в режиме реального времени решаются две задачи A и B с разной частотой решения. Задачи оформлены и запускаются как отдельные процедуры. Задача A решается в цикле длительности T0, задача B — в цикле длительности T1 = 4T0, но не ранее, чем в цикле длительности T1 будет решена один раз задача A. Можно предположить использование сигналов прерывания в моменты времени, кратные T0. Однако для организации временного режима решения задач мы воспользуемся возможностями операций над семафорами.

Будем полагать, что в моменты времени, кратные T0, но не кратные T1, запускается управляющий процесс (супервизор) УПР0, а в моменты времени, кратные T1, — управляющий процесс (супервизор) УПР1. Требуемая временная диаграмма решения задач представлена на рис. 11.2.


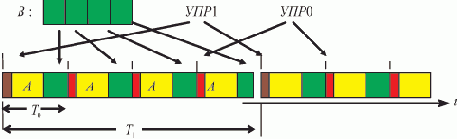
Рис. 11.2.  Синхронизация совместного решения задач в циклах разной длительности


Пусть предварительно объявлены семафоры D1, D2, A, B1, B2.

Тогда в каждом из процессов могут быть запланированы операции над семафорами, как показано на рис. 11.3.


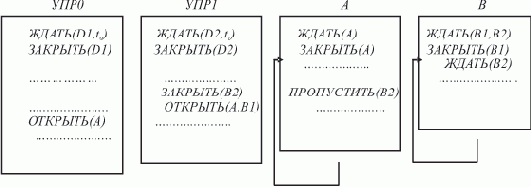
Рис. 11.3.  Использование операций над семафорами

Предположим, первоначально t0 = t1 = 0. Тогда из первых команд УПР0 видно, что он включается в моменты

T0, 2T0, 3T0, 5T0,... .

УПР1 включается в моменты

0, T1, 2T1,... .

Начальные значения семафоров A и B1 — "закрыт", семафора В2 — "открыт". Первоначально задачи A и B находятся в очереди "к процессору". При их назначении на процессор и при выполнении первых процедур ЖДАТЬ (А) и ЖДАТЬ (В1, В2) произойдет прерывание. После него задача A находится в очереди к семафору A, задача B — к семафору В1. Пусть приоритет задачи A выше приоритета задачи B. (Задачи, решаемые с большей частотой, как правило, снабжаются более высоким приоритетом.)

В момент времени, кратный T1, задача УПР1 закрывает семафор B2, но открывает семафоры A и B1. Задача A переводится в очередь "к процессору". Пусть одного процессора достаточно для выполнения всех задач. Тогда с учетом приоритета в мультипрограммном режиме задача В решается в промежутки времени, не занятые решением других задач. После выполнения задачи УПР1 начинается выполнение задачи A с закрытия семафора A. Так как до выполнения процедуры ЗАКРЫТЬ(А) семафор А имел значение "открыт", то прерывания выполнения задачи A не произойдет и она будет решена до конца. В конце ее решения по процедуре ПРОПУСТИТЬ(В2) откроется семафор B2 и задача B перейдет в очередь "к процессору". Задача A организована по принципу зацикливания, т.е. после ее окончания управление передается на ее начало с процедуры ЗАКРЫТЬ(А). Так как к моменту выполнения этой процедуры семафор A закрыт в результате ее предыдущего выполнения, произойдет прерывание и постановка задачи A в очередь к семафору A. Этот семафор откроется только при выполнении задачи УПР0 после увеличения текущего времени на T0.


При этом, т.к. открытие семафора A в задаче УПР0 производится процедурой ОТКРЫТЬ, а прерывание задачи A произошло по процедуре ЗАКРЫТЬ, то выполнение задачи A продолжится с выполнения процедуры ЗАКРЫТЬ(А). Таким образом, более чем однократное решение задачи A без прерывания вновь окажется невозможным.

Аналогично по принципу зацикливания организовано и решение задачи B. После однократного выполнения она будет прервана при повторном выполнении процедуры ЗАКРЫТЬ(В1). Семафор B1 откроется только при следующем выполнении задачи УПР1

после увеличения текущего времени на T. При этом выполнение задачи B продолжится с повторного выполнения процедуры ЗАКРЫТЬ(В1), т.к. семафор B1 открывается процедурой ОТКРЫТЬ. Однако продолжение выполнения задачи B станет возможным после открытия семафора B2. Он же окажется открытым только после однократного выполнения задачи A в цикле длительности T1 после выполнения процедуры ПРОПУСТИТЬ(В2) в конце решения задачи A. Использования этой процедуры в данном случае достаточно.

Таким образом, соблюдается требуемый порядок решения задач.

Теперь усложним пример. Предположим, что для решения задачи A одного процессора недостаточно и необходимо использовать возможности ее параллельного решения. Мы представляем эту задачу в виде частично упорядоченного множества информационно- взаимосвязанных работ — подзадач — и используем механизм семафоров для соблюдения порядка следования этих работ. При этом мы предполагаем, что в ВС реализовано децентрализованное диспетчирование, т.е. свободные процессоры обращаются за очередным заданием к очереди "к процессору". На рис. 11.4

представлена примерная граф-схема задачи на основе составляющих ее подзадач. Каждая вершина соответствует подзадаче. Стрелки определяют информационную преемственность. Процедура над семафорами, изображенная выше вершины, показывает, что соответствующая подзадача начинается с выполнения этой процедуры. Процедура, изображенная ниже вершины, показывает, что подзадача заканчивается выполнением этой процедуры.



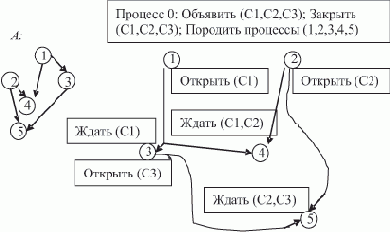
Рис. 11.4.  Синхронизация параллельных вычислений с помощью семафоров

3. Передача сообщений, "почтовый ящик". Метод " почтовых ящиков" является распространенной формой метода передачи сообщений.

Каждому процессу выделяется массив — "почтовый ящик", в который другие процессы направляют свои результаты или сигналы, необходимые для выполнения или запуска этого процесса.

Возможна реализация виртуальных процессоров. Свободный процессор опрашивает очередь подряд, т.е. в соответствии с невозрастанием приоритетов, и пытается запустить тот процесс, для которого в его "почтовом ящике" есть вся необходимая для этого информация. Либо же этот анализ может производить сам запускаемый процесс: если всей необходимой информации в его "почтовом ящике" нет, процесс прерывается и возвращается в очередь. Процессор продолжает циклический опрос очереди.

С помощью "почтовых ящиков" реализуется схема управления потоком данных (data flow), когда явное задание исходной информации для процесса является необходимым условием его запуска.

4. Механизм закрытия адресов. Осуществляется командой вида "закрыть адрес (по считыванию)". Адрес запоминается в специальном ЗУ, и при попытке считывания по нему производится ожидание — по аналогии с процедурой ЖУЖ. Открывается адрес по записи по нему. Для избежания тупиковых ситуаций, например,

ЗАКР a СЧИТАТЬ a

указывается номер того процессора, который закрыл адрес. Тогда есть возможность принять какое-то решение. Например, разрешить процессору, закрывшему адрес, открыть его.

Вернемся к примеру счета способом "пирамиды". Наметилось решение проблемы синхронизации: пусть счет очередного элемента предваряется командой, закрывающей адрес результата — считаемого элемента. Засылка найденного элемента откроет адрес. Тогда, пока этот элемент не будет получен, его адрес не сможет использоваться для счета других элементов.

Такой способ синхронизации был приведен при рассмотрении архитектуры SPMD.


5. Механизм активного ожидания.

Он основан на том, что к разделяемой (т.е. к общедоступной) ячейке ОП одновременно может обращаться по записи или считыванию только один процессор. При этом конфликт разрешается аппаратно: один обращается, остальные ждут. Тогда в ячейках можно хранить информацию о состоянии процессов. Процессы их могут анализировать и изменять.

Пример рассмотрим далее, совместив его с рассмотрением одной из задач синхронизации.

6. Монитор.

Монитор - скорее сервисное средство, позволяющее пользователю избежать заботы о синхронизации использования разделяемых ресурсов. Это программный компонент, в котором разделяемые переменные (представленные именами разделяемых ресурсов) определены как локальные переменные монитора. Определены операции над этими переменными - процедуры монитора. Одновременно только один процесс работает с монитором! Когда процессу требуется работать с разделяемой переменной, активизируется соответствующая процедура монитора. Если при обращении процесса к монитору ресурс занят, то вызывающий процесс должен быть задержан.

С каждой причиной задержки процесса связана специальная переменная типа CONDITION (условие), и задерживаемый процесс ставится в очередь к некоторой переменной этого типа.

К переменным указанного типа применяются операции WAIT и SIGNAL. Операция WAIT ставит процесс в очередь к данной переменной (например, указывающей на занятость соответствующего ресурса). Операция SIGNAL позволяет активизировать процесс (в случае, когда условие выполнено).

Задачи синхронизации

Известны типичные задачи синхронизации, к которым могут быть сведены практически все известные способы упорядочения работ во времени. Эти задачи, как правило, решаются при реализации второго способа распараллеливания.
1. Задача взаимного исключения. Имеется несколько процессов, программы которых содержат критические интервалы, где процессы обращаются к одному разделяемому критическому ресурсу (например, к базе знаний). Требуется исключить одновременное вхождение в такие критические интервалы более чем одного процесса.
Требования к решению этой задачи:

задержка любого процесса вне его критического интервала не должна влиять на развитие других процессов;

решение должно быть симметрично относительно процессов;

решение не должно допускать тупиков.

Решение с помощью механизма семафоров:
Для сравнения приведем альтернативный способ решения с помощью механизма активного ожидания.
Выделим ячейку памяти C, в которую будем записывать 0, если ни один из процессов не требует доступа к критическому ресурсу, и номер i того процесса (или выполняющего процессора), который вступил в свой критический интервал. Тогда условием вхождения i-го процесса в критический интервал является результат выполнения следующего оператора:

Действительно, если (C) = 0, то процесс может войти в критический интервал. Однако возможно, что через небольшое время другой процесс (на другом процессоре) тоже сделал такую же проверку и следом за первым произвел засылку в C своего номера. Поэтому требуется повторная проверка того, что в C находится именно номер данного процесса. При положительном результате повторного анализа процесс может вступить в критический интервал, т.е. занять критический ресурс. После выполнения критического интервала в C засылается 0.
С помощью механизма семафоров такая синхронизация выполняется значительно проще, т.к. многие действия предусмотрены внутри процедур их обработки.
2. Задача "поставщики — потребители". Имеется ограниченный буфер на несколько порций информации. Он является критическим ресурсом для процессов двух типов:

процессы "поставщики", получая доступ к ресурсу, помещают на свободное место в буфере несколько или одну порцию информации;

процессы "потребители", получая доступ к ресурсу, считывают из него порции информации.

Требуется исключить одновременный доступ к ресурсу любых двух процессов. При опустошении буфера следует задерживать процессы "потребители", при полном заполнении буфера — процессы "поставщики".
Эта задача возникает, например, при обмене с внешними устройствами и заключается в программной имитации кольцевого или бесконечного буфера.
Возможная схема решения задачи с помощью семафоров:
Имитация кольцевого (бесконечного) буфера показана на рис. 11.5.

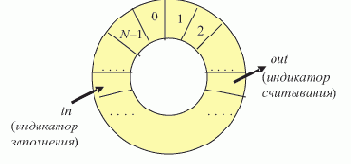
Рис. 11.5.  Кольцевой (бесконечный) буфер)
Тогда уточним данную процедуру с учетом используемых индикаторов считывания и заполнения.
3. Задача "читатели — писатели".
Имеется разделяемый ресурс — область памяти, к которой требуется доступ процессам двух типов:
Процессы первого типа — "ЧИТАТЕЛИ" — могут получать доступ к разделяемому ресурсу одновременно. Они считывают информацию.
Процессы второго типа — "ПИСАТЕЛИ" — взаимно исключают и друг друга, и "читателей". Они записывают в разделяемую область памяти данные.
Задача известна в двух вариантах:

"Читатели", изъявившие желание получить доступ к ресурсу, должны получить его как можно быстрее; это — первая задача ЧП.

2. "Читатели", изъявившие желание получить доступ к ресурсу, должны получить его как можно быстрее, если отсутствуют запросы от "писателей". "Писатель", требующий доступ к ресурсу, должен получить его как можно быстрее, но после обслуживания "читателей", подошедших к ресурсу до первого "писателя". Это — вторая задача ЧП.

Приведем возможное решение задач с помощью комбинированного семафора.
Считаем, что процедура ОТКРЫТЬ ПО СЧИТЫВАНИЮ выполняется подобно процедуре ПРОПУСТИТЬ, изменяя только значение семафора-счетчика. Процедура ОТКРЫТЬ ПО ЗАПИСИ выполняется подобно процедуре ОТКРЫТЬ, "открывая" семафор и обеспечивая запуск "задержанных" процессов с процедур ЗАКРЫТЬ ПО ЗАПИСИ или ЖДАТЬ ПО ЗАПИСИ, при выполнении которых произошло прерывание.
Тогда критические интервалы для каждой задачи могут быть выполнены по следующим схемам.

4. Задача "обедающие философы". За круглым столом сидят k философов, которые проводят время, чередуя философские размышления с потреблением пищи. Перед каждым — тарелка спагетти, между тарелками — по одной вилке. Для еды каждому философу требуются две вилки. Использовать можно только вилки, лежащие рядом с тарелками. Так как переходы от размышления к принятию пищи производятся в непредсказуемые моменты времени, то возможны конфликты и требуется синхронизация процессов.
Представим следующую модель, требующую решение данной задачи, — модель оперативного обмена между процессорами векторной ВС или строк (столбцов) матричной ВС (рис. 11.6).

Рис. 11.6.  Связь по схеме "обедающие философы"
Например, после счета очередного элемента в узле сетки результаты должны быть переданы соседним процессорным элементам для использования в следующей итерации. Очевидна возможность конфликтов при попытке одновременной встречной передачи.
Пусть с i-м процессором для передачи влево связан "левый" семафор Ci, для передачи вправо — "правый" семафор Ci+1 (или наоборот). Пусть каждый процессор, нуждающийся в передаче двум соседям, пытается сначала закрыть свой "правый" (аналогично, "левый") семафор. Затем, если это не успел сделать левый сосед, он попытается закрыть "левый" семафор и произвести передачу. Тогда возможен общий тупик, если все процессоры одновременно закроют все семафоры. (При одновременном пересчете значений функции в узлах сетки вероятность такой ситуации высока.)
Разрешим четным процессорам сначала закрывать "левые" ("правые") семафоры, а нечетным — "правые" ("левые"). Тогда схемы программ для них будут выглядеть следующим образом:

Пусть процессор с нечетным номером i нуждается в обмене — влево и вправо. Он пытается выполнить процедуру ЗАКРЫТЬ(Ci+1). Предположим, что этот семафор (для него — "правый") закрыт i+1-м процессором. Но для этого процессора с четным номером этот семафор — также первый в порядке закрытия ("левый"). Следовательно, он либо ждет возможности закрытия своего "правого" семафора, либо ведет обмен. Если он ждет своего "правого" семафора, то он его дождется, т.к. он — второй для процессора i+2, ведущего обмен. Значит, этот процессор закончит обмен и откроет свой "левый" семафор. Тогда процессор i+1 выполнит обмен и откроет семафор Ci+1. Тогда и процессор i, наконец, сможет выполнить необходимую процедуру. После этого он попытается выполнить процедуру ЗАКРЫТЬ(Ci). Этот семафор является "правым", т.е. вторым для процессора с четным номером i-1. Следовательно, этот процессор закрыл оба связанных с ним семафора и ведет обмен. По окончании обмена он откроет семафоры, и процессор i дождется необходимого "левого" семафора и сможет его закрыть для себя. Таким образом, тупиковая ситуация возникнуть не может.
Обычно n — степень двойки. Если же n нечетно, то на границе n - 1 взаимодействуют два "нечетных" процесса обмена. Здесь возможна блокировка, когда процессор 1 закроет C2, а процессор n — семафор C1 (1 = (n+1)mod n). Однако, процессор n обязательно дождется открытия семафора Cn и выполнит обмен. Значит и процессор 1 дождется открытия семафора C1, выполнит обмен и откроет C2. Так что тупики и в данном случае исключены.
Рассмотрение данной задачи синхронизации выводит нас за рамки традиционного применения мультипроцессорной системы типа MIMD, к каким относятся, например, ВС семейства "Эльбрус". Однако универсальность такой архитектуры допускает принципиальную возможность воспроизведения на ней более "жестких" архитектур — матричных и векторных, т.е. типа SIMD. Реализация метода "сеток" на матричных ВС или на структурах типа "гиперкуб" требует подобной передачи не только двум соседним процессорам по строке, но и соседним по столбцу, по диагонали и т.д. Значит, возможно обобщение данной задачи и алгоритма синхронизации. Указанный выше прием разделения процессоров на четные и нечетные может быть применен по всем направлениям обмена — по строкам, по столбцам, по диагонали и т.д.
5.Задача обновления данных. Предполагает запрет на использование обновляемых данных. Например, процессор обновляет запись в базе данных. В простейшем случае может быть использован признак, по которому запрещается обращение к данной записи, пока она не будет обновлена. (Конечно, мы не рассматриваем того примитивного решения, когда БД превращается в ресурс с последовательным доступом. Мы стремимся к многоканальному, параллельному доступу.)
Вместо признака может быть использован семафор. Ожидание может быть организовано процедурами ЖДАТЬ или ЖУЖ.

Параллельное программирование

Оценка надежностных характеристик ВС при испытаниях

Согласуют контрольную задачу (КЗ) или комплекс КЗ, с помощью которых будут производить испытание ВС. В основу КЗ берут те алгоритмы или их аналоги, которые как можно ближе соответствуют назначению ВС в составе системы управления. Хороших показателей испытаний добиваются тогда, когда в состав КЗ включают модели управляемых объектов и таким образом строят замкнутый контур управления объектом. Модели объектов могут учитывать случайные возмущения, и, следовательно, управление становится реальным. Такие КЗ наглядны, результативны, бесспорны, поскольку опираются на принцип "удача — неудача".

Согласуют определение основных событий и состояний. Например,

малый рестарт считать обнаруженным сбоем с восстановлением;

"неудачный" цикл управления считать сбоем без восстановления;

большой рестарт считать отказом, где его время — время восстановления;

выход из конфигурации числа процессоров, снижающих более чем на 20% производительность ВС (2 процессора из 10 в МВК "Эльбрус-2"), считать отказом;

реконфигурацию, не снижающую более чем на 20% производительность, считать отказом с переходом на резерв;

Аналогичные соглашения принимаются и насчет памяти, внешней памяти, ПВВ и ППД, обеспечивающих выполнение КЗ.

Объявляют прогон — циклическое непрерывное решение КЗ (комплекса КЗ) в течение значительного времени (например, 5 суток), достаточного для набора статистики.

Набирают статистику по ВС в целом и по группам устройств. Обычно разграничивают центральную часть и периферию. Непосредственно снимают те показатели, о которых говорилось выше:

среднее время T0 безотказной работы;

среднее время Tвосст восстановления;

частоту ?1 сбоев; из них — число "восстановленных" для определения Pвосст;

частоту ?2 отказов, из них — число приведших к успешной реконфигурации для нахождения Pрез.

По приведенным выше формулам мы можем получить необходимые показатели надежности.

Оценка производительности ВС

Если несколько процессоров составляют ВС, то важной характеристикой ее эффективности эффективности (основные составляющие эффективности — производительность, надежность, стоимость) при специализированном использовании (например, в составе АСУ) является коэффициент загрузки процессоров kЗ. Для его определения находят коэффициенты загрузки процессоров
где T i, i = 1, ..., n — время занятости каждого процессора решением задачи на всем отрезке полного решения задачи, длиной Tреш
(рис. 12.1).

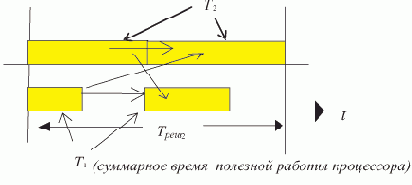
Рис. 12.1.  К эффективности загрузки процессоров
Тогда
Если P0 — производительность одного процессора, то реальная производительность ВС, состоящей из n процессоров, при решении данной задачи (!) составляет
PBC = n kЗ P0.
P0 определяется классом решаемых задач.
Идеальным способом его определения является использование самих задач. Однако при предварительной оценке возможностей ВС может еще не существовать алгоритмов той системы, в которой предполагается использовать ВС. Либо класс решаемых задач может быть достаточно широк.
Известны несколько подходов к формированию тестов, по которым определяется производительность P0 единичных ЭВМ или процессоров ВС.

Смеси операций различных типов в случайном порядке, отражающие их процентное соотношение в задачах интересующего класса.
Для вычислительных задач применялась (утвержденная ГОСТом) смесь "Гибсон-3". Она хорошо отражала архитектуру ЕС ЭВМ, воспроизводящей архитектуру IBM. Однако ранее говорилось о тенденции повышения уровня языка пользователя, об аппаратной поддержке ЯВУ. Смесь Гибсона, приведенная ниже, не отражает этих тенденций. Набор операций примитивен, соответствует ЭВМ ранних поколений. Интерпретация в ней "языковых" операций затруднительна и уменьшает точность оценки. Ее использование определялось требованиями советских ГОСТов.
Смесь "Гибсон-3"

1.	Загрузка регистра без индексации	31 %
2.	Загрузка регистра с индексацией	18 %
3.	Проверка условия и переход	17 %
4.	Сравнение	4 %
5.	Сдвиг на 3 разряда	4 %
6.	Логическая операция "И"	2 %
7.	Команды с минимальным временем выполнения	5 %
8.	Сложение с фиксированной запятой	6 %
9.	Умножение с фиксированной запятой	0,6 %
10.	Деление с фиксированной запятой	0,2 %
11.	Сложение с плавающей запятой	7 %
12.	Умножение с плавающей запятой	4 %
13.	Деление с плавающей запятой	1,5 %

Приведенная смесь Гибсона интересна статистически произведенными оценками состава операций в решаемых задачах вычислительного характера. Это полезно знать и в других случаях выбора и оценки архитектурных решений.

Известен принцип построения тестов на основе смеси по методу Ветстоуна, где в состав операций входят операции, реализующие сложные языковые конструкции.

Ядра. Ядро — небольшая программа, часть решаемой задачи. Характеристики ядра могут быть точно измерены. Известны ядра Ауэрбаха: коррекция последовательного файла и файла на диске, сортировка, обращение матрицы и др.

Бенчмарки — реальные программы, характеристики которых можно оценить или измерить при использовании. Обычно берут из числа тех, для которых разрабатывается система.

Программа синтетической нагрузки — параметрически настраиваемая программа, представляющая смеси определенных программных конструкций. Позволяет воссоздать набор вычислительных характеристик, свойственных большинству программ, для решения которых используется или разрабатывается ВС.

У нас в стране в аналогичном применении больше известна модель вычислительной нагрузки.

Она применяется на уровне решения вопроса: какие вычислительные средства поставить в систему или заказать их разработку?

Модель позволяет перейти с уровня оценки одного процессора ВС на уровень комплексной оценки ВС. Составляется и параметризуется с учетом сложной структуры ВС и ее устройств, параллельного участия этих устройств в решении задач, доли участия и порядка взаимодействия устройств.

Например, на основе статистических оценок решаемых в системе управления частных задач (функциональных модулей) строится обобщенная модель программы, в которой возможна следующая параметрическая настройка:

среднее количество непрерываемых операций, выполняемых процессором;

частота обращений к ОП, связанных с запуском механизмов виртуальной памяти, возможностью конфликтов в связи с расслоением памяти, мультипроцессорной обработкой;

частота обращений к ОС (для организации выполнения процедур на стеке, индексации массивов, обращения к очереди "к процессору", мультипрограммного режима, синхронизации в режиме реального времени, отработки прерываний, счета стандартных функций и др.) и связанные с этим потери полезной производительности;

сценарий параллельного ввода-вывода информации с учетом ее объема;

частота или сценарий внутрисистемного обмена, связанного с необходимостью синхронизации работ в совокупности с параллельным выполнением;

количество процессоров и других функциональных устройств в системе.

Однако все эти тесты не дают ответ на традиционный вопрос: какое количество операций в секунду выполняет ВС? Все усложняющаяся структура и расширяющееся множество "нетрадиционных" операций затрудняют ответ.

Тогда особую важность обретают сравнительные оценки исследуемой ВС с другими ЭВМ или ВС, для которых уже известны значения производительности по числу операций в секунду.

Итак, структурные средства повышения уровня языка, параллелизм работы устройств, введение дополнительных операций все с меньшей определенностью соответствуют традиционным тестам.

Пример — проблема оценки ЦП с многофункциональным АЛУ: как их загружать для реальной оценки (сколько их реально будут загружено в каждом такте), какой поток обмена с ОП предполагать и т.д.?

Используется сравнительная оценка характеристик решения задачи на исследуемой ВС и на ВС или ЭВМ, для которой уже известны характеристики производительности.

Одна и та же задача решается на известной ЭВМ, для которой (из-за ее более простой организации) известно значение производительности или быстродействия; например, ЕС 1066 имеет производительность 5,5 млн оп./с. Однопроцессорный МВК "Эльбрус-2" контрольную физическую задачу решает за 6,5 часа, ЕС 1066 — за 21 час. Значит, эквивалентная производительность "Эльбрус-2" в комплектации с единственным процессором составляет ? 5,5 ? 21/6,5 = 17,6 млн оп./с (в сравнении с ЕС 1066). Аналогично проводилось сравнение с ЭВМ БЭСМ-6.

На этапе испытаний ВС при оценке производительности складывается больше определенности по будущему режиму ее эксплуатации. Есть возможность построения контрольной задачи (КЗ), (развивающей идеи бенчмарок), использующую всю ВС. КЗ строится на основе типовых задач аналогичных систем управления, использует развиваемый прототип системы, воссоздает реальный режим решения. Для КЗ оценивается количество так называемых алгоритмических операций (аналог того, что отражено в смеси Ветстоуна). Т.е. можно максимально приблизить вычислительную нагрузку ВС к реальной ожидаемой.Это — современный комплексный подход, когда КЗ, составленная для всей ВС как для единой установки, учитывает не только использование процессоров, но и затраты на организацию вычислительного процесса, издержки ОС, интенсивность параллельного обмена информацией, организацию помехозащищенного вычислительного процесса.

Относительно последнего следует подчеркнуть: строятся контрольные задачи, по которым производительность оценивается с учетом надежности.

Особенности обеспечения надежности ВС

Выше мы предположили, что для ЭВМ все сказанное бесспорно и во многом очевидно. Переход к многопроцессорным ВС требует дополнительных разъяснений.
Построение многопроцессорных ВС (в России — семейства МВК "Эльбрус") привело к пересмотру всех традиционных представлений о надежности.
С одной стороны, большой объем оборудования при недостатках элементной базы приводит к резкому возрастанию сбоев и отказов в устройствах и модулях, с другой стороны — структурная и функциональная избыточность, виртуализация ресурсов, управление распределением работ, аппаратный контроль предназначены для выполнения устойчивого вычислительного процесса.
В этих условиях подвергаются сомнению сами определения сбоя и отказа. Эти определения принимаются по согласованию между разработчиком ВС и системщиком, т.е. с учетом требований тех задач, которые должна решать ВС в составе, например, системы управления.
Вышел из строя один из 10 процессоров ВС, — отказ ли это ВС? Ответ зависит от конкретной системы, решаемых задач, временного режима их решения, от требований к производительности, принимаемых мер по обеспечению устойчивого вычислительного процесса и т.д. Произошел сбой процессора, при котором сработал малый рестарт, перезапустивший весь процесс или процесс с контрольной точки. Потери времени на этот рестарт не приведут к необратимому нарушению работы всей системы? Т.е. это — действительно сбой или отказ? Тем более сбои в работе ОС или та категория сбоев, которая приводит к перезапуску ВС — к большому рестарту: загрузке ОС и работе с начала. В "Эльбрусе-2" большой рестарт выполняется более чем за 3 секунды. К чему это отнести — к сбою или отказу? Это зависит от системы, в которой используется ВС.
Таким образом, в проблемно-ориентированных ВС проблема сбоев и отказов решается комплексно в соответствии с применением ВС.
Использование в ВС большого числа однотипных устройств с учетом идеи виртуальных ресурсов вносит особенности и в понятие резервирования. Реализуется структурное резервирование (развивает идеи скользящего резервирования), на основе которого при отказах производится реконфигурация системы: продолжение ее функционирования при изменившемся количестве устройств одной специализации.
В этом смысле говорят о "живучести" системы.

В связи с изложенным, в МВК "Эльбрус-2" одним из механизмов, обеспечивающих "живучесть" комплекса, является система автоматической реконфигурации и перезапуска при сбоях и отказах (САР). Она включает в себя специальную аппаратуру, распределенную по модулям МВК, системные шины, программные средства ОС.

Аппаратно выполняются следующие действия:

Обнаружение аварии в модуле, определение ее типа, сохранение диагностической информации и приостановка работы аварийного модуля.

Передача информации об аварии по специальным шинам (а мы думали, что связь между модулями ВС — только через коммутатор!) в другие модули.

Обработка сигналов аварии, приходящих от других модулей и исключение аварийного модуля из конфигурации.

Системная реакция на аварию: либо запуск специальных процедур ОС (малый рестарт), либо перезапуск комплекса (большой рестарт).

Программно выполняются следующие действия:

Сбор и обработка диагностической информации аварийного модуля.

Попытка вернуть его в рабочую конфигурацию в предположении, что авария — в результате сбоя.

Сохранение в системном журнале информации об аварии.

Таким образом, в САР предусмотрены различные реакции на разные типы аварий.

Возникновение асинхронной аварии на процессе пользователя ведет к автоматическому исключению неисправного модуля из конфигурации и к запуску процедуры ОС, обрабатывающей аварийную ситуацию и определяющей дальнейшее течение аварийного процесса — аварийное завершение или перезапуск (малый рестарт). Остальные процессы "не чувствуют" аварийной работы. Исключение составляет случай, когда в конфигурации представлен лишь один модуль некоторого типа. Возникновение в нем аварии приводит к перезапуску всего комплекса (к большому рестарту).

Возникновение асинхронной аварии на процессе ОС всегда завершается большим рестартом.

Помехоустойчивые вычисления

Поскольку мы не занимаемся разработкой и эксплуатацией ВС как комплекса радиоэлектронной аппаратуры, рассмотрим проблемы оценки и повышения надежности ВС как средства решения конкретных специальных задач.
В этом смысле под надежностью ВС будем понимать вероятность решения поставленной перед ней задачи.
Тогда надежность ВС в составе сложной системы управления определяется следующими факторами:

вероятностью пребывания в исправном состоянии в момент начала цикла управления;

вероятностью пребывания в исправном состоянии в течение всего цикла управления;

помехоустойчивостью, т.е. способностью с допустимыми потерями временных, точностных и аппаратурных ресурсов на требуемом качественном уровне завершить цикл управления при возникновении неисправностей.

Построим дерево логических возможностей (рис. 12.2) для нахождения всех вероятностных составляющих вычислительного процесса в ВС.

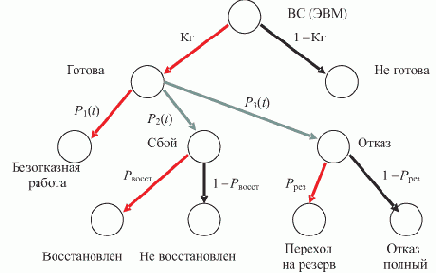
Рис. 12.2.  Дерево логических возможностей для расчёта надёжности
(Дерево логических возможностей строится следующим образом. При исходе из одной вершины на каждом уровне ветвления вводится исчерпывающее множество событий, т.е. сумма их вероятностей равна единице. Вероятности событий проставляются на дугах. Тогда вероятность интересующей нас совокупности событий находится как сумма произведений вероятностей, отмечающих пути, которые ведут к данным событиям. Пример проиллюстрирует сказанное выше.)

Одной из определяющих характеристик надежности является коэффициент готовности К Г

где Tвосст — среднее время восстановления (в т.ч. ремонта) после отказа. Т.е. к началу цикла управления с вероятностью КГ ВС приступит к решению своей задачи.

Если ВС приступила к решению задачи, то возможны три варианта:

в течение всего времени t решения задачи (или t — цикл управления) ВС работала безотказно. Т.е. без каких-либо осложнений задача решена в предположении, что программы составлены правильно;

произошел сбой (не усложняя проблемы, учитывая обычную быстротечность процессов, считаем, что сбой — единственный);

произошел отказ.

Примечание. Сбой — самоустранимый отказ. В результате случайных наводок в некоторой цепи может появиться или пропасть сигнал. Сбои приводят (по классификации разработчиков МВК "Эльбрус") к синхронным и асинхронным авариям. При синхронной аварии (ее вызывают преимущественно сбои в ЦП) может быть установлена и повторена команда, при исполнении которой авария произошла. При многочисленных передачах информации внутри ВС используются коды, исправляющие ошибки. Значит, в этом случае сбои также приводят к синхронным авариям.

При асинхронной аварии вычислительный процесс нарушается необратимо. При должном уровне аппаратного контроля современных ВС синхронные аварии считаются "невидимыми" пользователю — команды перезапускаются аппаратным контролем.

Примечание. Приведенные ниже выкладки хорошо известны и бесспорны для отдельных ЭВМ (однопроцессорных ВС). Поэтому в последующих разделах будет показано, как они обобщаются и переносятся на общий случай ВС.

Напомним модель надежности.

Пусть ?1 — частота сбоев (количество сбоев в единицу времени), найденная как одна из характеристик данной ЭВМ; ?2 — частота отказов; ?1 + ?2 = ?. Тогда ? t — количество сбоев и отказов за интересующее нас время t— цикл управления.

Разобьем отрезок t на множество n элементарных отрезков. Можно считать вероятность сбоя или отказа на таком элементарном отрезке равной ?t/ n. Вероятность бессбойной и безотказной работы на элементарном отрезке равна 1 ? ?t/ n. Вероятность того, что на всех элементарных отрезках не произойдет сбоя или отказа, приведет к нахождению степени n этого выражения, а далее найдем предел (рис. 12.3)


Рис. 12.3.  К нахождению вероятности безотказной работы

Тогда p2(t)+ p3(t) = 1 - e-? t , и разделив пропорционально частотам событий, получим

Запишем полную вероятность успешного решения задачи (надежность), сложив произведения вероятностей по всем путям в дереве логических возможностей, ведущим к событиям с благоприятным исходом:

P = KГ P1(t) + KГ P2(t) Pвосст + KГ P3(t) Pрез = KГ(P1(t) + P2(t)Pвосст + P3(t)Pрез).


Здесь присутствуют величины, которые полностью характеризуют организацию помехозащищенного вычислительного процесса.

Защита от сбоев . Самым надежным и испытанным приемом защиты от последствий сбоев является двойной просчет. Он характерен для ЭВМ, не обладающих аппаратным контролем. В случае несовпадения результатов двойного просчета задача считается третий раз.

Практически (в АСУ) времени для этого нет. Используют методы программного (алгоритмического) контроля. Например, пусть производится интегрирование уравнения движения летательного аппарата с необходимой точностью. После получения очередных значений координат производится приближенная линейная экстраполяция для получения тех же координат на основе предыдущих положений объекта. Тогда точно полученные координаты должны попасть в определенную - окрестность координат, полученных приближенно. Так производится оценка достоверности результатов. Т.е. программно-алгоритмический контроль основан на способности предсказания ограниченной области, которой должны принадлежать результаты счета.

В современных ВС, как правило, используется аппаратный контроль, который устраняет синхронные аварии и сигнализирует о асинхронных авариях, порождая сигнал прерывания. Отметим сразу, что вероятность обнаружения сбоя или неисправности аппаратным контролем меньше единицы (является его характеристикой), но это не исключает применения методов, о которых говорилось выше.

Как правило, использование сигнала аппаратного контроля следующее. Программа делится на сегменты некоторого рекомендуемого объема - по времени выполнения и по количеству команд программы, — разделенные контрольными точками. Выход на контрольную точку сопровождается запоминанием или дублированием всей необходимой информации для того, чтобы следующий сегмент мог при необходимости перезапуститься (произвести малый рестарт), если во время его выполнения произойдет сбой. Используют при этом и расслоение памяти, запоминая необходимые данные для рестарта в других модулях памяти, т.е.


предусматривая возможность отказов модулей памяти. Рестарт с предыдущей (т.е. ближайшей) контрольной точки производится только в случае сбоя и в целом требует затрат значительно меньших, чем двойной просчет и программно-алгоритмический контроль.

Резервирование. Применяется во всех ответственных случаях специального использования ВС. В дополнение к одной, основной ЭВМ используются одна и более резервных. Резервные, как правило, не связаны с внешними объектами или объектами управления. С ними связана основная, а они могут дублировать ее работу, реализуя двойной просчет с анализом на совпадение или участвуя в мажоритарной схеме контроля, когда общее число ЭВМ больше двух и когда с помощью мажоритарного устройства на выходе всех ЭВМ производится "голосование": результаты счета считаются правильными, если получены большинством ЭВМ.

Иногда резервируют не отдельно ЭВМ, а весь комплекс — ЭВМ плюс внешние устройства памяти, связи и обмена. Такой комплекс называют линейкой.

Различают горячий и холодный резерв.

В горячем резерве ЭВМ работает в режиме дублирования или решения вспомогательных задач и в любой момент готова взять функции основной. В холодном резерве машина отключена.

Повышение характеристик надежности управляющего ВК можно видеть на примере роста коэффициента готовности ВК. Пусть для одной ЭВМ К Г = 0,9.

Тогда использование двух (одна резервная) одинаковых ЭВМ обеспечивает

KГ(2) = 1 - (1 - KГ)2 = 0,99("две девятки");

Использование трех (две резервные) одинаковых ЭВМ обеспечивает

KГ(3) = 1 - (1 - KГ)3 = 0,999 ("три девятки").

Если в системе несколько ЭВМ, то каждая из них может иметь одну или более резервных. Это — распределенный резерв.

Но возможен скользящий резерв, когда несколько ЭВМ являются резервными, и каждая из них способна заменить каждую из основных. Количество резервных ЭВМ в этом случае согласуется с ?-характеристикой ЭВМ и количеством основных ЭВМ и приводит к созданию более надежных и более дешевых комплексов.

Параллельное программирование

Параллельное программирование

Уже известны разработки3), поддерживающие сложные распределенные базы данных для многоканального использования. Одним из проектов является разработка Oracle 10G, предназначенная для реализации коммерческой Grid-системы. Ее механизмы поддерживают следующие подсистемы и функции:

Grid хранения данных;

Grid серверов БД;

Grid серверов приложений;

Средства самонастройки узлов БД;

Систему управления Grid;

Средства для разделения информации между узлами Grid.

Проанализируем, что из изложенного в данном курсе материала о параллельных информационных технологиях можно использовать в рамках рассматриваемого направления исследований.
Прежде всего, предполагая, что целью исследований является не просто сервисная поддержка, а оптимизация информационного обслуживания, необходимо сформулировать критерий оптимизации. Логично выбрать таким критерием минимум среднего времени выполнения единичного запроса с учетом времени его обработки поисковой системой.
Но ведь именно в таком свете представляется проблема минимизации времени обращения к базе данных, изложенная в лекции 2! И там математически, на основе теории массового обслуживания, доказано, что активизация совокупной памяти БД посредством "встречной" циркуляции сегментов не только обеспечивает синхронизацию независимого многоканального доступа, но, главное, способствует медленному, вполне приемлемому росту времени выполнения запроса в зависимости от роста числа абонентов. (В противном случае это время быстро стремится к бесконечности.)
Было показано, что одним из методов построения БД с циркулирующей информацией является объединение серверов в единую замкнутую систему — в "кольцо", по которому циркулируют сегменты этой базы. Абоненты же жестко связаны со своими серверами, обеспечивая распределенные, примерно равные, потоки запросов на каждый сервер. По каждому запросу должно учитываться среднее время ожидания нужного сегмента за счет его циркуляции.
Тогда можно себе представить следующую схему функционирования гипотетической Ассоциации Web-серверов (рис. 13.1), объединенных на основе гигантской совокупной базы данных, мирового (или хотя бы корпоративного) масштаба. Учитывая все возрастающую мощность серверов и, главное, — средств передачи данных, можно уже сегодня ожидать значительного сокращения числа отказов при выполнении запросов, требующих сложного многоступенчатого трафика, зависящего от пропускной способности многих промежуточных пунктов.

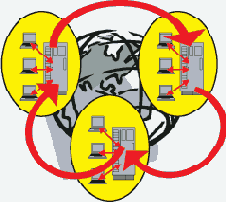
Рис. 13.1.  Ассоциация Web-серверов мирового информационного пространства

Известные проекты Grid-технологии решения вычислительных задач

Grid-технологии, быстро распространяясь, завоевывают ключевые позиции в области высоких технологий во всем мире, утверждая приоритетное развитие всей широкой области информационных технологий (ИТ) как локомотива государственного процветания.
Итак, система Grid-вычислений — это распределенная программно-аппаратная компьютерная среда, с принципиально новой организацией вычислений и управления потоком заданий и данных.
Поучительным примером практического воплощения концепции Grid может служить глобальный проект China Grid, запущенный корпорацией IBM совместно с министерством образования Китая в целях повышения эффективности научно-исследовательской и образовательной деятельности ведущих китайских университетов. Grid-система, построенная на операционной платформе Linux, обеспечивает интегрированную, открытую, виртуализованную и автономную рабочую среду. Ею должно быть охвачено около 100 учебных заведений по всей стране, что вовлечет в проект более 200 тысяч студентов и преподавателей. Благодаря China Grid китайские университеты надеются сократить расходы на научно-исследовательские и опытно-конструкторские работы.
Отечественным примером реализации рассматриваемой технологии может служить экспериментальный Grid-сегмент МГУ им. М.В.Ломоносова 4).
В основе этого проекта лежит проект EDG (EU Data GRID — европейский проект для физики высоких энергий, биоинформатики и системы наблюдений за Землей). В свою очередь, им используется проект Globus (разработчик — Argonne National Lab.), предоставляющий инструментальные средства связи, информационного обслуживания, безопасности, управления ресурсами, локального управления ресурсами и заданиями.
Программное обеспечение Globus доступно и распространяется свободно.
Проект EDG предполагает формирование вычислительных ресурсов на основе анализа сайтов организаций, подразделений, вычислительных узлов.
Типичный сайт содержит следующие разделы информации.

Компьютер конечного пользователя, позволяющий пользователю взаимодействовать с Grid-средой, в частности, запускать задания и получать результаты.

Вычислительный элемент, представляющий ссылку на Grid-интерфейс к локальной системе управления пакетной обработкой (СУПО).

Рабочие узлы, входящие в состав вычислительного элемента и управляемые с помощью СУПО, что скрыто от пользователя.

Накопитель данных, управляющий единообразным доступом к любым устройствам памяти.

Брокер ресурсов, принимающий задания от пользователя, согласующий требования к ресурсам, которые содержатся в описании задания, с имеющимися, и направляющий задания на подходящий сайт вычислительного элемента.

Каталог реплик, поддерживающий базу данных о местах хранения оригинальных файлов и всех их копий.

Чтобы получить доступ к ресурсам МГУ-GRID, необходим компьютер с установленным пользовательским Grid-интерфейсом. Доступ в среду Grid происходит под именем, содержащимся в сертификате, и контролируется с помощью специальной программы-посредника (электронной доверенности), которая создается на ограниченный срок с помощью персонального ключа пользователя.
Файл с описанием задания создается с помощью языка описания заданий (Job Description Language) и содержит необходимые входные данные, требования к ресурсам и сведения о том, куда должны быть записаны результаты обработки задания.

Немного истории

Первые опыты в области Grid-технологий связаны с расчетами экспериментов в ядерной физике. Считается, что этот опыт вообще стал базой формирования World Wide Web, WWW — Всемирной Паутины. С ним связывают имя: Тим Бернес-Ли. Перед этим ученым была поставлена задача найти способ, который позволил бы ученым, участвующим в экспериментах на Большом адронном коллайдере, обмениваться данными и представлять результаты их обработки на всеобщее обсуждение. Многие физики, большую часть времени находящиеся в своих научных институтах, тоже хотели полноправно участвовать в анализе данных.
Тим Бернес-Ли предложил создать в Европейской организации ядерных исследований (CERN) систему распределенного информационного обеспечения, основанную на использовании гипертекста и способную объединить научные центры всей Земли. Были написаны специальные программы, установленные на многих компьютерах мира, которые были разбиты на группы, связанные со своим сервером. Эти программы могли работать с единой БД CERN, с помощью дополнительных серверов перерабатывая данные и возвращая результаты в единую БД.
В 1990 году прототип того, что впоследствии получило название Всемирной Паутины, был создан в CERN, а начиная с 1991 года, первые браузеры и WWW-серверы появились в распоряжении ядерных физиков всего мира. Широкое распространение сразу же получили язык HTML и протокол HTTP.
Однако теоретическое обобщение опыта CERN и развитие идеи WWW в область современного представления о будущей сети Grid, было сделано американскими учеными Яном Фостером и Карлом Кессельманомe2). По их представлению, Grid действительно является "надстройкой" над Интернетом, предназначенной для распределенных вычислений при решении задач высокой сложности в области науки и технологий.
В отличие от бесструктурной паутины WWW, решетка Grid строго упорядочена. Характерно, что разделения на информационные задачи и задачи вычислительные авторы не предполагают. Пользователь, подключаясь к Grid, получает доступ к миллионам компьютеров, как для вычислений, так и для хранения данных, добытых в результате решения, и для размещения огромных массивов информации. Первостепенное внимание уделяется проблемам безопасности, анонимности, секретности.

Основные направления исследований в области Grid-технологий

Термин "Grid-вычисления" (Computing grid), где "grid" означает "решетка, сетка, сеть", по смыслу аналогичен выражению "единая энергосистема". Суть его заключается в стремлении объединить все компьютеры мира в единую систему — в виртуальный суперкомпьютер невиданной мощности, что позволит распределять и перераспределять ресурсы между пользователями в соответствии с их запросами. Именно так человечество пользуется электричеством единых энергетических сетей. Основу подобного объединения можно рассматривать и для транспортных сетей, сетей обеспечения водой, нефтью, газом и т.д.
Имея такой суперкомпьютер, пользователь может в любое время и в любом месте запросить столько вычислительных ресурсов, сколько ему требуется для решения своей задачи. Более того, он может заказать ее решение, послав запрос-заявку на сайт одного из центров обслуживания. Так же, как единая энергосистема локально испытывает переменную нагрузку (потребление электроэнергии в отдельной стране, регионе или населенном пункте изменяется в зависимости от времени суток, года и т.д.), так и система Grid-вычислений способна перераспределять мощности, направляя запросы на недогруженные компьютеры в соответствии с возросшими требованиями.
Предоставление вычислительных ресурсов по требованию связывают с известным понятием "коммунальная услуга", что вполне соответствует тенденции объединения и распределения ресурсов жизнеобеспечения.
Однако на Grid-технологии возложены задачи и информационного характера: сделать всю информацию мира оперативно доступной. Это означает, что пользователь должен ощущать, что вся информация, за которой он обратился, находится здесь, рядом, не далее чем на сервере того провайдера, к которому он подключен.
И мы ловим себя на мысли, что говорим об Интернете!
Да, в сущности, речь идет о смелом, фантастическом развитии именно того, что фантастическим казалось вчера, о развитии всемирной паутины, о внедрении в нее вычислительных функций и о повышении качества информационного обслуживания.
Именно так и намечается дальнейший путь развития Интернета: от WWW к GRID1).

Таким образом, для Grid-технологии характерны два (традиционно смешиваемых) направления развития, определяемые их важностью и различиями в исследовании.

Первое направление, связанное с информационными задачами, представляет сегодня сущность Интернета. Это — обмен новостями, приобретение новых знаний, программных средств, мульти-медиа-развлечения, диалоговые системы телеконференции, электронная почта, финансовые операции и т.д. Эти функции "Всемирной Паутины" уже представляются достаточными самым широким слоям населения, покрывая весь компьютерный сервис. Они органично вошли в базовое воспитание детей, определяя уровень грамотности современного человека.

Однако именно здесь существует основная проблема. Неуправляемое стихийное, даже "дикое" развитие Интернета приводит к парадоксу: доступность огромных объемов мировой информации породила значительный вес отказов, ответов о действительной недоступности этой информации, о превышении допустимого времени поиска, об ошибках. Поисковые системы блуждают по иерархической, запутанной системе Web-серверов, натыкаясь на их перегрузку, образуя трафик для обратного движения информации. Мы с отчаянием следим за замершей планкой индикатора, в ожидании выдачи такой знакомой записи "Error..." — с указанием предположения об окончании допустимого времени адресного обращения.

Сделать всю информацию доступной, установить гарантированное время поиска, породить у пользователя ощущение того, что вся информация по его запросу находится рядом, — это фантастическая задача. Можно ли объединить всю информацию мира, блуждающую в Интернете, в одну огромную базу данных, размеры которой даже трудно оценить? Да еще с неограниченным многоканальным доступом?

Движение в направлении осуществления этой глобальной идеи и является задачей исследователей в области Grid-технологий. Ясно, что идеального решения эта задача может никогда не получить. Однако стремиться к минимизации времени выполнения запроса, несмотря на структурную "удаленность" информации, несомненно, следует.


Второе направление развития Grid- технологий связано, как ранее говорилось, с таким расширением функций Интернета, при котором пользователь может получать ответы на запросы вычислительного характера. Речь, конечно, идет о тех задачах, решение которых недоступно широкому пользователю — ученому, управленцу, коллективу, всем, кому необходима достоверная информация для важных решений. Интернет должен принимать заказ на работу с задачами высокой сложности, большой размерности, с задачами моделирования сложных физических явлений, таких, например, как точный метеорологический прогноз, с оптимизационными задачами хозяйственного планирования, с задачами статистической обработки экспериментов, с задачами — запросами по контролю космического пространства, с имитационными задачами для испытания новых технических средств и т.д.

Это означает, что в составе Интернета должны быть мощные вычислительные центры, снабженные развиваемыми пакетами прикладных программ решения сложных задач, оболочками для решения классов задач. Такие центры должны комплектоваться высококвалифицированными математиками, развивающими вычислительную базу, готовыми принимать заказы, консультировать пользователей при "доводке" заказов до требуемого формального представления, ибо мечты о полной автоматизации процесса их выполнения еще долго будут неисполнимыми.

Необходимо учесть и селекцию допустимых заказов: при желании, например, отстранить школьника-разгильдяя, препоручающего выполнение урока домашнему компьютеру.

При построении Grid-систем особую актуальность обретают проблемы защиты. Цель защиты — перекрыть доступ к ресурсам и информации для тех пользователей, которые не имеют соответствующих привилегий. Таким пользователем может стать и собственник, предоставивший свой компьютер в аренду или по договору на время простоя.

Базовыми элементами защиты являются:

аутентификация — проверка подлинности участника взаимодействия с системой;

механизм авторизации — проверка допустимости затребованной операции;

конфиденциальность и целостность данных — защита от нелегитимного доступа;

биллинг и аудит — способность контролировать и подсчитывать объем использованных ресурсов и обеспечиваемых ими служб;

строгое выполнение обязательств — способность устанавливать, что данный участник выполнил определенную задачу или согласился на ее выполнение, даже если сам он это отрицает.

Основы проектирования Центра Grid-технологий

В подходе к реализации идеи Grid-технологий наблюдается некоторая поспешность. Не существует формального анализа возможных видов запросов, слабо выражено разделение на информационные и вычислительные задачи.
Материал предыдущих лекций говорит, что все алгоритмы и все работы, выполняемые с помощью вычислительных средств, структурированы. Недостаточно связывать выполнение запроса на решение задачи только лишь с выделением вычислительных ресурсов. Ими надо управлять, а вычислительный процесс — распараллеливать.
В лекции 8 представлена общая схема параллельного вычислительного процесса, из которой видно обязательное наличие двух управляющих элементов: супервизора и диспетчера. Супервизор управляет ходом вычислительного процесса, реализуя его функциональную направленность. Диспетчер управляет использованием вычислительных ресурсов.
В отличие от задач перераспределения энергии, которые подобны задачам оптимального использования бригады землекопов, роющих большую яму, задачи распараллеливания вычислений, как указывалось выше, сталкиваются с основной трудностью: с необходимостью соблюдения частичной упорядоченности работ, с необходимостью решения конкретных задач синхронизации (лекция 11).
Первые опыты применения Grid-вычислений, сходные с опытом Тима Бернес-Ли, позволяли распределять между компьютерами мира работы, мало связанные между собой. Это были независимые эксперименты, большие массивы данных. Тем не менее, результаты возвращались и обрабатывались централизованно. Это — весьма простая схема распараллеливания по информации, примитивный аналог SPMD-технологии. В общем случае, даже при реализации этой технологии, являющейся воплощением распараллеливания по информации, невозможно избежать синхронизации по общим данным. Механизмы синхронизации должны работать быстро, что требует конкретного анализа возможности и целесообразности решения задач на основе виртуального ресурса Интернет. Это замечание говорит в пользу идеи концентрации вычислительных ресурсов.
Сообразуясь с требованиями практической целесообразности, необходимо уяснить, какого типа бывают запросы вычислительного характера к Grid-системам (рис. 13.2).


Рис. 13.2.  Типы запросов к системе Grid -вычислений

Представим себе, что Пользователь заходит на сайт крупной GRID-Компании. Его желания могут быть следующими:

Он готов, например, арендовать ресурс для построения задуманной им автоматизированной системы управления железнодорожным транспортом. Пользователь в диалоговом режиме подробно излагает требуемые характеристики, в том числе и количественные.

Компания на основе своих возможностей согласует с пользователем предоставляемую услугу. Далее следуют договоренности финансового и юридического характера.

Таким образом, пользователь, получив подробное описание предоставленных ему ресурсов, сам работает с ними, введя по необходимости их адресацию или применяя принцип виртуальности, - по замыслу создаваемой системы. При этом, разумеется, он обладает средствами взаимодействия между отдельными средствами для организации нужной ему схемы вычислений.

Пользователь хочет решить или решать периодически, с заданным темпом, по динамически изменяемым исходным данным, транспортную задачу (проблему Хичкока) с известными ограничениями пропускной способности магистралей. Обращаясь к данной компании, он предполагает наличие в ее пакете прикладных программ (ППП) нужной программы, да еще решаемой быстро на основе применения метода распараллеливания. Он вступает в диалог с Компанией, уточняя постановку задачи, условия ее решения, режим решения, обещает продолжить отношения в случае успешного опыта, согласует условия оплаты и т.д.

Если условия ему не нравятся, пользователь обращается к сайту другой компании.

Пользователь хочет решить конкретную задачу нахождения экстремума функции от 1020 переменных на положительной области, ограниченной 524 гиперплоскостями и заданной системой дифференциальных уравнений в частных производных второго порядка. Обращаясь к Компании, пользователь может рассчитывать лишь на наличие оболочек, в которые можно погружать конкретные условия задачи и описывающие выражения.

В диалоговом режиме высококвалифицированный консультант предлагает решить задачу в два этапа: сначала с помощью существующей оболочки найти решение системы дифференциальных уравнений, а затем, с помощью другой оболочки, найти экстремум.


Если пользователь согласен на все условия относительно времени решения и оплаты, заключается договор. Правда, в договоре должна быть предусмотрена ситуация, когда в процессе решения выясняется некорректность задания исходных данных, неразрешимость, неоднозначность решения и т.д. Такие ситуации требуют дальнейших консультаций, уточнения постановки задачи и величины оплаты, а, возможно, и расторжения договора, после чего могут следовать значительные юридические и финансовые тяжбы.

Пользователь знает алгоритм решения своей задачи, описанный на языке Паскаль. Он ничего не желает знать об используемых ресурсах, он хочет получить трехмерный массив результатов решения или место его хранения. О статистической обработке и построении диаграмм он пока не думает, оставляя этот вопрос в рамках решения о целесообразности дальнейшего сотрудничества с Компанией.

Обработка такого запроса пользователя более всего приятна Компании, которая, не чувствуя ответственности, может выдать ответ о некорректности записи алгоритма или об ошибках.

Пользователь обращается за решением задачи по физике за IX класс. Компания может предоставлять и такую услугу — по неформальной постановке задачи. Высококвалифицированный специалист (пользуясь совершенным справочником), выполнив нехитрые вычисления, в диалоговом режиме разъяснит пользователю необходимость родительских гарантий в части предоплаты и изложит свое мнение об издержках воспитания.

Домохозяйка просит о льготной помощи при расчете оплаты коммунальных услуг, исходя из текущего тарифа, с опережением указываемых расходов электроэнергии, горячей и холодной воды на случай непременного и скорого его повышения. Компания, в лице опытного консультанта, вступившего в диалог, располагая возможностями финансовых услуг по известным, постоянно обновляемым данным, предлагает оплатить не 112 квт, а 200, т.к. тариф в следующем месяце повысится, а указанный расход лежит в пределах критически допустимого. В этом смысле Grid-технология действительно вторгается в сферу коммунальных услуг.

На основе этих примеров можно заключить, что задачи нашей гипотетической Grid-Компании, которую точнее следует назвать "Центр GRID-Технологий", весьма широки и многообразны. Приведем ряд принципов его деятельности и некоторые пункты его обоснования.

Необходимость (и неизбежность) таких компаний, владеющих большим арсеналом вычислительных средств, очевидна. Обезличенного обращения в Интернете не бывает. Кто-то должен обрабатывать запросы.

Такая компания, по-видимому, являясь акционерным обществом, в свою очередь, может арендовать средства более мелких собственников, а также сетевое оборудование, системы передачи данных, включая космические.

Рассмотрим, какие вычислительные средства должны составлять собственную технологическую базу Центра.

Центр, несомненно, должен объединять решение информационных и вычислительных задач. Поэтому наличие Web-серверов и участие их во Всемирной или Региональной ассоциации обязательно.

Что касается исключительно вычислительных задач, то здесь, как говорилось выше, ресурс может быть составлен на договорной основе, на базе фактически разрозненных вычислительных средств организаций и отдельных собственников.

Однако основной капитал Центра GRID-Технологий определяется собственными вычислительными средствами и сопутствующим оборудованием. Его комплектование и развитие определяется двумя возможными направлениями:

комплектацией на базе перспективных или разрабатываемых суперкомпьютеров и многопроцессорных вычислительных систем на их основе;

комплектацией на базе существующего, стремительно развивающегося парка компьютеров, рабочих станций и серверов, которые с помощью сопутствующего сетевого оборудования объединены в локальную вычислительную сеть, реализующую распределенные вычисления. Это направление, не отрицающее первое, несомненно, более перспективно.

Центр должен быть укомплектован высококвалифицированными математиками-программистами и системотехниками, работающими по нескольким направлениям:

оперативное консультирование пользователей при "доводке" заданий;

разработка пакета прикладных программ и оболочек;

сотрудничество с пользователями при совместной разработке сложных программных и информационных проектов;

научно-исследовательская деятельность по развитию Grid-технологий и их применению;

Проанализировав материалы лекций, обозначим тот пакет прикладных программ и оболочек, который может быть предложен Центру GRID-Технологий. Это:

решение систем линейных уравнений;

задачи сортировки и поиска;

параллельный логический вывод;

параллельные технологии решения задач линейного программирования;

параллельные технологии решения задач целочисленного линейного программирования;

параллельные технологии решения транспортной задачи без ограничений и с ограничениями пропускной способности магистралей;

параллельные технологии нахождения максимальной пропускной способности сети;

методы точного решения задач распараллеливания как задач сетевого планирования и управления;

задачи оперативного параллельного планирования — задачи диспетчирования;

оболочка: конечно-разностные методы решения систем дифференциальных уравнений;

оболочка: параллельная технология решения оптимизационной задачи нелинейного программирования при линейных ограничениях;

оболочка: параллельная технология решения "плоской" оптимизационной задачи нелинейного программирования при нелинейных ограничениях (легко развивается на случаи большей размерности);

оболочка: параллельный ПРОЛОГ;

оболочка: расчет величины возбуждения нейронов нейросети.

Следует отметить также предлагаемые многочисленные алгоритмы и схемы организации параллельных вычислений в ВС и процессорах различной архитектуры, а также способы построения параллельных управляющих процессов с учетом их синхронизации.

  1)

  Петрушанко С. CERN: от WWW к GRID. "Компьютерра", 2004, \No21.

  2)

  Forster I., Kesselman K., "The Grid: Blueprint for a New Computing Infrastructure". Morgan Kaufmann, 1998.

  3)

  Ривкин М. ORACLE и коммерческая GRID, http://mrivkin.narod.ru.

  4)

  Экспериментальный Grid-сегмент МГУ им. М.В.Ломоносова. Руководство для пользователей. GRID — сеть для МГУ, ComNew.ru



    Программирование: Языки - Технологии - Разработка

• Программирование
  
• Технологии программирования
  
• Разработка программ
  
• Работа с данными
  
• Методы программирования
  
  
• IDE интерфейс
  
• Графический интерфейс
  
• Программирование интерфейсов
  
• Отладка программ
  
• Тестирование программ
  
  
• Программирование на Delphi
  
• Программирование в ActionScript
  
• Assembler
  
• Basic
  
• Pascal
  
  
• Perl
  
• VBA
  
• VRML
  
• XML
  
• Ada
  
  
• Lisp
  
• Python
  
• UML
  
• Форт
  
• Языки программирования