Формальные языки
Исключение цепных правил
| Определение. Правило грамматики вида ® , где , ОVA, называется цепным. |
| Утверждение. Для КС-грамматики Г, содержащей цепные правила , можно построить эквивалентную ей грамматику Г', не содержащую цепных правил. |
Идея доказательства заключается в следующем. Если схема грамматики имеет вид
R = {..., ®
,..., ®
},
то такая грамматика эквивалентна грамматике со схемой
R' = {..., ®
a
поскольку вывод в грамматике со схемой R цепочки a
Ю<
B> Ю
Ю a
может быть получен в грамматике со схемой R' с помощью правила
® a
В общем случае доказательство последнего утверждения можно выполнить так.
Разобьем R на два подмножества R1 и R2, включая в R1 все правила вида ® < B>.
Для каждого правила из R1 найдем множество правил S(
если
*
® a
, где a - цепочка словаря (Vт
ИVA)* ,
то в S(
Построим новую схему R' путем объединения правил R2 и всех построенных
множеств S(
заданной и не содержит правил вида ®
.
В качестве примера выполним исключение цепных правил из грамматики
Г1. 9
со схемой :
Г1. 9:
R={
< T> ® < T> *
Вначале разобьем правила грамматики на два подмножества:
R1 = {
R2 = {
Для каждого правила из R1 построим соответствующее подмножество.
S(
T>*
S(
(
В результате получаем искомую схему грамматики без цепных правил в виде:
R2 U S(
-->
(
Последний вид рассматриваемых преобразований связан с удалением из
грамматики правил с пустой правой частью.
|
Определение. Правило вида ® $ называется аннулирующим правилом. |
След.Страница Раздел Содержание
Исключение леворекурсивных правил
| Определение. Правило вида ® a , где A О VA , a О(Vт ИVA) * , называется праворекурсивным, а правило вида ® a - леворекурсивным. |
| Утверждение. Для каждой КС-грамматики Г, содержащей леворекурсивные правила, можно построить эквивалентную грамматику Г', не содержащую леворекурсивных правил. |
Способ построения эквивалентной грамматики заключается в следующем. Допустим, что исходная грамматика Г содержит
правила:
®
a 1 | a
2 | ... |a m| ,
где ни одна цепочка b не начинается с
и a1, b1О(Vт ИVA) * .
Введем новый нетерминал
®
b 1 | b
2 |...| b n | b
1
1 | a 2 |...| a
m| a 1
2
Заменяя все правила с левой рекурсией в Г описанным способом, получим грамматику Г',
причем L(Г)=L(Г') , поскольку каждая цепочка, выведенная в грамматике Г, может быть
построена в грамматике Г'. Рассмотрим построение выводов в Г и Г'. В грамматике Г вывод
цепочки имеет вид:
< A> Ю a 1 Ю
a 1a
1 Ю a 1a
1a 1 Ю b 1a
1a 1a
1,
в грамматике Г' эта же цепочка выводится так:
Ю
b 1
b 1a 1
Ю b
1a 1a
1
b 1a
1a 1a
1.
Чтобы показать технику преобразования, рассмотрим пример. Требуется преобразовать
грамматику Г1. 9 (рассмотренную ранее), которая задана схемой:
Г1. 9: R={
< T> ®
Следуя описанному способу, правила
®
+
®
F> | *
В результате получаем грамматику Г'1. 9, имеющую схему:
Г'1. 9 : R'= {
< T>,
< E'>® +
< F> ® a,
(
не содержащую леворекурсивных правил.
Пред.Страница
След.Страница Раздел Содержание
Язык, допускаемый магазинным автоматом
| Определение. Цепочка a называется допустимой для автомата М, если существует последовательность конфигураций, в которой первая конфигурация является начальной c цепочкой a , а последняя - заключительной. (sо, a, hо) |--* (s1, $ , $) , где s1 О F . |
| Определение.Множество цепочек, допускаемых автоматом М, называется языком, допускаемым или определяемым автоматом М, и обозначается L(М). |
L(М)= {a ¦ ( sо, a, hо ) ¦--* ( s', $, $) & s' О F }
Чтобы лучше представить себе работу магазинного автомата, рассмотрим два примера. Пусть задан магазинный автомат М1 в следующем виде:
М1: P = {a , b}; S = {s0 , s1 , s2}; H = {h0 , a}; F = {s0};
f (s0 , a , h0) = (s1 , h0a),
f (s1 , a , a) = (s1 , aa),
f (s1 , b , a) = (s2 , $),
f (s2 , b , a) = (s2 , $),
f (s2 , e
, h0) = (s0 , $).
Этот автомат является детерминированным, поскольку каждому набору аргументов соответствует единственное значение функции. Работу автомата при распознавании входной цепочки aabb можно представить в виде последовательности конфигураций:
(s0,aabb,h0) |-- (s1,abb,h0a) |-- (s1,bb,h0aa) |-- (s2,b,h0a) |-- (s2,$,h0) |-- (s0,$,$) .
Нетрудно проверить, что при задании входной цепочки aabbb автомат не сможет закончить работу. Следовательно эта цепочка не принадлежит языку, допускаемому автоматом M1.
Магазинный автомат М2, заданный следующим описанием:
М2: P = {a , b}; S = {s0, s1 , s2}; H = {h0, a , b}; F = {s2};
(1)f (s0 , a , h0) = (s0, h0a),
(2)f (s0 , b , h0) = (s0, h0b),
(3) f (s0 , a , a) = {(s0,aa) , (s1 , $)},
(4) f (s0 , b , a) = (s0,ab),
(5) f (s0 , a , b) = (s0 , ba),
(6) f (s0 , b , b) = {(s0 , bb) , (s1 , $)},
(7) f (s1 , a , a) = (s1, $),
(8) f (s1 , b , b) = (s1, $),
(9) f (s2 , e
, h0) = (s2 , $),
является недетерминированным автоматом, поскольку одному и тому же набору аргументов, например (sо , a, a), соответствуют два значения функции.
Работу автомата рассмотрим для входной цепочки abba. Если использовать последовательность команд (1),(4),(6.1),(5), то получим последовательность конфигураций:
(s0,abba,h0) |-- (s0,bba,h0a), (1)
|-- (s0,ba,h0ab), (4)
|-- (s0,a,h0abb), (6.1)
|-- (s0,$,h0abba). (5),
которая показывает, что дальнейшая работа невозможна, т.к. входная цепочка прочитана и переход (s0,$,h0abba) не определен. Если же использовать последовательность команд (1),(4),(6.2),(3),(9), то получим заключительную конфигурацию:
(s0,abba,h0) |-- (s0,bba,h0a), (1)
|-- (s0,ba,h0ab), (4)
|-- (s1,a,h0a), (6.2)
|-- (s1,$,h0), (3)
|-- (s2,$,$) . (9).
Т.о. можно сделать вывод о том, что цепочка abba допускается автоматом М2.
В общем случае справедливо следующее утверждение.
Пред.Страница
След.Страница Раздел Содержание
Магазинные автоматы
КС-грамматика определяет структуру цепочек и позволяет строить цепочки определенного языка. Магазинные автоматы, подобно рассмотренным ранее конечным автоматам, позволяют решать для контекстно-свободных языков задачу распознавания, которая заключается в том, что по заданной цепочке необходимо определить принадлежит ли она заданному языку.
В работах, связанных с формальными языками и грамматиками,используется модель магазинного автомата, состоящая из входной ленты, устройства
управления и вспомогательной ленты, называемой магазином
или стеком.
Входная лента
разделяется на клетки (позиции) , в каждой из которых может быть
записан символ входного алфавита. При этом предполагается, что в неиспользуемых клетках входной ленты расположены пустые символы e.
Вспомогательная лента также разделена на клетки, в которых могут располагаться символы магазинного алфавита. Начало вспомогательной ленты называется дном
магазина. Связь устройства управления с лентами осуществляется двумя головками, которые могут перемещаться вдоль лент.
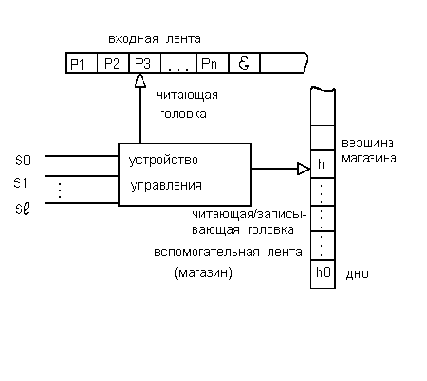
Головка входной ленты может перемещаться только в одну сторону - вправо или
оставаться на месте. Она может выполнять только чтение. Головка вспомогательной ленты способна выполнять как чтение, так и запись, но эти операции связаны с перемещением головки определенным образом:
- при записи головка предварительно сдвигается на одну позицию вверх, а затем символ заносится на ленту,
- при чтении символ, находящийся под головкой считывается с ленты, а затем головка сдвигается на одну позицию вниз,т.о.головка всегда установлена против последнего записанного символа. Позицию, находящуюся в рассматриваемый момент времени под головкой, называют
вершиной магазина.
| Определение.Магазинный автомат М определяется следующей совокупностью семи объектов: M={P , S , sо , f , F , H , hо }, |
где
P - входной алфавит,
S - алфавит состояний,
sо - начальное состояние,
sо О S ,
F - множество конечных состояний ,F является подмножеством S,
H - алфавит
магазинных символов, записываемых на вспомогательную ленту,
hо- маркер дна, он всегда записывается на дно магазина , hо О H,
f - функция переходов
f : {P И {e
}} x S x H ® S x H* ,
если М-автомат - детерминированный, и
f:{P И {e
}} x S x H ® M(S x H*) ,
если М-автомат - недетерминированный. Функция f отображает тройки ( pi , sj , hk ) в пары ( sr , u
) , где u О
H* и hk - символ в вершине магазина, для детерминированного автомата или в множество пар для недетерминированного автомата.
Эта функция описывает изменение состояния магазинного автомата, происходящее при чтении символа с входной ленты и премещении входной головки.
В дальнейшем при построении магазинных автоматов потребуются две разновидности функций переходов, изменяющих состояние автомата без перемещения входной головки: 1) функция переходов с пустым символом в качестве входного символа:
f0( s, e, h) = ( s', b),
которая, независимо от того какой символ находится под читаюшей гловкой входной ленты, предписывает прочитать символ h
из вершины магазина, изменить состояние автомата на s' и записать цепочку
b в магазин.
2)функция переходов с определенным входным символом:
f*( s, a, h) = ( s', b),
которая предписывает изменение состояния и запись цепочки в магазин при условии, что символ a читается входной головкой, а в вершине магазина находится символ h .
Пред.Страница
След.Страница Раздел Содержание
Определение непроизводящих символов
Рассматривая правила грамматики, можно сделать вывод, что если все символы правой части являются производящими, то производящим является и символ, стоящий в левой части. Последнее утверждение позволяет написать процедуру обнаружения непроизводящих символов в следующем виде:
1. Составить список нетерминалов, для которых найдется хотя бы одно правило, правая часть которого не содержит нетерминалов.
2. Если найдено такое правило, что все нетерминалы, стоящие в его правой части уже занесены в список, то добавить в список нетерминал, стоящий в его левой части.
3. Если на шаге 2 список больше не пополняется, то получен список всех производящих нетерминалов грамматики, а все нетерминалы не попавшие в него являются непроизводящими.
Анализируя в соответствии с приведенными правилами следующую грамматику :
Г2. 0: R = {®aa,
®bd,
®c,
®cd,
®ad,
®df },
находим, что здесь непроизводящими являются символы <А> и <В>. После удаления правил, содержащих непроизводящии символы, получаем:
R' = { ®aa, ® c}.
Пред.Страница
След.Страница Раздел Содержание
Определения бесполезных символов
Бесполезный символ грамматики можно определить следующим образом:
| Определение. Символ X, который принадлежит VтU Va называется бесполезным в КС-грамматике Г, если он является недостижимым или непроизводящим. |
Исключить бесполезные символы из грамматики можно удаляя правила, содержащие вначале непроизводящие, а затем недостижимые символы. В качестве иллюстрации применения приведенных правил выполним преобразование следующей грамматики:
Г2. 2 : R = {®ac,
® b,
® c
® a,
Вначале находим, что <А> и <В> являются непроизводящими символами и, исключая правила с непроизводящими символами , получаем:
R' = {®ac,
В полученной схеме символ
R" = {®ac }.
| Определение. КС-грамматика называется приведенной, если она не содержит бесполезных символов. |
В дальнейшем изложении рассматриваются только
приведенные КС-грамматики. Другие виды преобразований грамматик, описываемые ниже, предназначены для исключения правил определенного вида из схемы грамматики.
Пред.Страница
След.Страница Раздел Содержание
Определения недостижимых символов
| Определение. Символ X О VтИ VA называется недостижимым в КС-грамматике Г, если X не появляется ни в одной выводимой цепочке. |
Рассматривая правила грамматики, можно заметить , что если нетерминал в левой части правила является достижимым , то и все символы правой части являются достижимыми. Это свойство правил является основой процедуры выявления недостижимых символов, которую можно записать так:
Образовать одноэлементный список, состоящий из начального символа
Если найдено правило, левая часть которого уже имеется в списке, то включить в список все символы, содержащиеся в его правой части.
Если на шаге 2 новые нетерминалы в список больше не добавляются, то получен список всех достижимых нетерминалов, а нетерминалы, не попавшие в список, являются недостижимыми.
Например, применяя приведенные правила к следующей грамматике:
Г2. 1 : R = { ®ab,
®c,
®b,
®a },
находим, что A является недостижимым символом.
Пред.Страница
След.Страница Раздел Содержание
Построение магазинного автомата
| Утверждение. Если Г = { Vт , Va , I , R } является КС-грамматикой, то по ней можно построить такой магазинный автомат М, что L(M) = L(Г). |
В основе доказательства лежит способ построения магазинного автомата по заданной КС-грамматике.Чтобы сделать процесс построения автомата более простым и наглядным, условимся использовать магазинные автоматы с одним состоянием s0. Итак, пусть задана грамматика Г = { Vт , Va , I , R }. Определим компоненты автомата М следующим образом: S = { s0 }, P = Vт , H = VтИ VaИ { h0} , F = { s0 },
в качестве начального состояния автомата примем s0 и построим функцию переходов так:
1. Для всех A О
VA , таких что встречаются в левой части правил
® a
, построим команды вида:
f0( s 0 , e
, ) = ( s0 , aR
),
где aR
-зеркальное отображение a
.
2. Для всех a ОVт
построим команды вида
f ( s0 , a , a ) = ( s0 , $ )
3. Для перехода в конечное состояние построим команду
f ( s0 , e , h0 ) = ( s0 , $ )
4. Начальную конфигурацию автомата определим в виде:
( s0 , w , h0 ),
где w - заданная цепочка, записанная на входной ленте.
Автомат, построенный по приведенным выше правилам, работает следующим образом. Если в вершине магазина находится терминал, и символ, читаемый с входной ленты, совпадает с ним, то по команде типа (2) терминал удаляется из магазина, а входная головка сдвигается. Если же в вершине магазина находится нетерминал, то выполняется команда типа (1), которая вместо терминала записывает в магазин цепочку, представляющую собой правую часть правила грамматики. Следовательно, автомат, последовательно заменяя нетерминалы, появляющиеся в вершине магазина, строит в магазине левый вывод входной цепочки, удаляя полученные терминальные символы, совпадающие с символами входной цепочки. Это означает, что каждая цепочка, которая может быть получена с помощью левого вывода в грамматике Г, допускается построенным автоматом М.
Пред.Страница
След.Страница Раздел Содержание
Преобразование неукорачивающих грамматик
| Определение. Грамматика называется неукорачивающей или грамматикой без аннулирующих правил, если либо 1)схема грамматики не содержит аннулирующих правил, 2)либо схема грамматики содержит только одно правило вида ® $, где - начальный символ грамматики, и символ I не встречается в правых частях остальных правил грамматики. |
Для грамматик, содержащих аннулирующие правила, справедливо следующее утверждение.
| Утверждение. Для каждой КС-грамматики Г', содержащей аннулирующие правила, можно построить эквивалентную ей неукорачивающую грамматику Г, такую что L(Г')=L(Г). |
Построение неукорачивающей грамматики предполагает увеличение числа правил заданной
грамматики путем построения дополнительных правил, получаемых в результате исключения
нетерминалов аннулирующих правил. Чтобы построить дополнительные правила необходимо
выполнить все возможные подстановки пустой цепочки вместо аннулирующего нетерминала во все правила грамматики. Если же в грамматике есть правило вида ®
$ и символ входит в правые части других правил грамматики, то следует ввести новый начальный символ
$ двумя новыми правилами:
$ и
.
В качестве иллюстрации способа построения неукорачивающих грамматик, исключим аннулирующие правила из следующей грамматики:
Г2. 3 : R = { ®
ab,
® ba,
Пример построения автомата
Процедуру построения автомата рассмотрим на примере грамматики:
Г1. 9: R={
*
(
Для искомого автомата имеем:
M3: P = {a, + , * , ) , ( }, H = {E , T , F , a , + , x , ) , h0 , ( }, S = {s0 }, F = {s0}
Для всех правил грамматики строим команды типа (1):
(1) f0
(s0 , e , E) = {(s0 , T+E) ; (s0 , T)},
(2) f0
(s0 , e , T) = {(s0 , F*T) ; (s0 , F)},
(3) f0
(s0 , e , F) = {(s0 , )E( ) ; (s0 , a)},
Для всех терминальных символов строим команды типа (2):
(4) f ( s0, a, a ) = ( s0, $ ),
(5) f ( s0 , + , + ) = (s0 , $ ),
(6) f ( s0 , * , * ) = (s0 , $ ),
(7) f ( s0 , ( , ( ) = (s0 , $ ),
(8) f ( s0 , ) , ) ) = (s0 , $ ),
Для перехода в конечное состояние построим команду:
(9) f (s0 , e
, h0) = ( s0 , $ ).
Построенный автомат является недетерминированным.
Начальную конфигурацию с цепочкой a + a*a запишем так: (s0 , a+a*a , h0E).
Последовательность тактов работы построенного автомата, показывающая, что заданная цепочка допустима, имеет вид:
(s0 , a+a*a , h0E) |-- (s0 , a+a*a , h0T+E) |--
(s0 , a+a*a , h0T+T) |-- (s0 , a+a*a , h0T+F) |--
(s0 , a+a*a , h0T+a) |-- (s0 , +a*a , h0T+) |--
(s0 , a*a , h0T) |-- (s0 , a*a , h0F*T) |--
(s0 , a*a , h0F*F) |-- (s0 , a*a , h0F*a) |--
(s0 , *a , h0F* ) |-- (s0 , a , h0F) |--
(s0 , a , h0a) |-- (s0 , $ , h0) |--
(s0 , $ , $).
Отметим, что последовательность правил, используемая построенным автоматом, соответствует левому выводу входной цепочки:
E Ю E+T Ю T+T Ю
F+T Ю a+T Ю a+T*F Ю a+F*F Ю a+a*F Ю a+a*a.
Если по такому выводу строить дерево, то построение будет происходить
сверху вниз, т.е. от корня дерева к листьям.
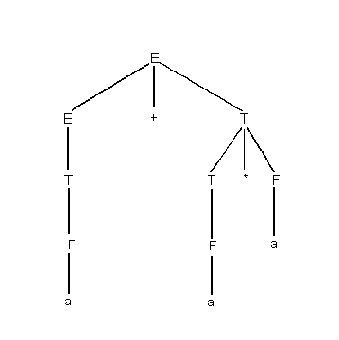
Такой способ построения дерева по заданной цепочке называется нисходящим.
Магазинные автоматы называют часто распознавателями, поскольку они определяют, является ли цепочка, подаваемая на вход автомата, допустимой или нет, и следовательно, отвечают на вопрос, принадлежит ли эта цепочка языку, пораждаемому грамматикой, использованной для построения автомата.
Учитывая характер построения вывода в магазине, автоматы рассмотренного типа называют нисходящими распознавателями.
Еще раз подчеркнем , что доказательство допустимости цепочки нисходящим магазинным автоматом ( НМА) предусматривает поиск определенной последовательности конфигураций.
Такой поиск может существенно увеличить время работы автомата. Детерминированные автоматы не требуют поиска и работают быстрее, поэтому именно такие автоматы применяются на практике. Детерминированные автоматы-распознаватели могут быть построены не для всех, а только для некоторых видов КС-грамматик.
|
Определение. Если язык L допускается детерминированным М-автоматом , то он называется детерминированным языком. |
Учитывая значение детерминированных автоматов для практических применений, посвятим им последующие разделы.
Пред.Страница
След.Страница Раздел Содержание
Приведенные грамматики
Из четырех типов грамматик контекстно-свободные грамматики являются наиболее важными с точки зрения приложений к языкам программирования и компиляции. С помощью КС-грамматики можно определить большую часть структуры языка программирования. При построении грамматик, задающих конструкции языков программирования, часто приходится прибегать к их преобразованию, чтобы порождаемый язык приобрел нужную структуру, поэтому вначале рассмотрим несколько достаточно простых, но важных преобразований КС-грамматик. Первый вид преобразования связан с удалением из грамматики бесполезных символов. Бесполезные символы в грамматике могут оказаться в следующих случаях: а) если символ не может быть получен при выводе,
б) если из символа не может быть получена конечная терминальная цепочка (получается бесконечная цепочка или нет правил,приводящих к терминальной цепочке).
Вначале рассмотрим алгоритм выявления символов, из которых нельзя вывести конечные
цепочки.
Пред.Страница След.Страница Раздел Содержание
Работа магазинного автомата
Чтобы описать как работает автомат, введем понятие конфигурации.
| Определение. Конфигурацией автомата М называют тройку (s, a , g ) О S x P* x H* , |
где s - текущее состояние управляющего устройства,
a -неиспользованная часть входной цепочки a
О P* ,самый левый символ этой цепочки a находится под головкой. Если a =e , то считается, что входная цепочка прочитана.
g -цепочка , записанная в магазине, g
О H* ,самый правый символ цепочки считается вершиной магазина. Если g=
$ , то магазин пуст.
Работа автомата может быть представлена как смена конфигураций. Один такт работы автомата заключается в определении новой конфигурации по заданной. Это записывается так:
( s, aa , g h ) |-- ( s', a , gb )
При этом предполагается, что автомат читает символ a, находящийся под головкой, и символ h,
находящийся в вершине магазина, определяет новое состояние s'
и записывает цепочку b
в
магазин вместо символа h. Если b =$ , то верхний символ оказывается удаленным из магазина.
Такая смена конфигураций возможна, если функция f( s, a, h ) определена и ей принадлежит
значение ( s', b ).
Описанный такт работы выполняется с перемещением головки. Для описания работы автомата нам потребуется другой вид такта, предполагающий изменение состояний и магазина без перемещения входной головки. Если f0(s, e, h) определена и ей принадлежит значение (s', b )
, то он определяет смену конфигураций так:
( s, aa , g
h ) |-- ( s', aa , gb )
Таким образом, могут быть три случая при работе автомата:
f(s, a, h) определена и выполняется такт работы,
f(s, a, h) не определена, но определена функция f0(s, e, h) и выполняется пустой такт.
Функции f(s, a, h) и f0(s, e, h)
не определены, в этом случае дальнейшая работа автомата невозможна.
В общем виде действия, задаваемые функцией переходов и выполняемые автоматом, демонстрирует следующая форма записи:
f(s, <входной символ>, <магазинный символ>)=(s1, <заносимая цепочка>)
При этом следует иметь в виду, что при выполнении такта вначале читается символ в вершине, а затем на его место заносится новый символ или цепочка. Отдельные значения функции переходов часто называют командами магазинного автомата.
Начальной конфигурацией называется конфигурация (sо, a
, hо) , где sо
-начальное состояние и hо
- маркер дна магазина, а заключительной - конфигурация (s, $ , $) , где s принадлежит множеству конечных состояний F.
Для обозначения последовательности сменяющих друг друга конфигураций условимся
использовать знак |--*. Таким образом последовательность
( s1, a 1, g
1 ) |-- ( s2, a 2, g 2) |-- ...|-- ( sn, a n,g
n )
записывается в сокращенном виде так:
(s1,a
1, g 1 ) |--* ( sn, a n,g
n ).
Пред.Страница
След.Страница Раздел Содержание
свободные языки являются более сильным
Контекстно- свободные языки являются более сильным выразительным средством, чем автоматные языки, которые являются подмножеством КС-языков. КС-грамматики, предназначенные для практических применений, не должны содержать бесполезных символов. Такие грамматики называются приведенными. КС-грамматики допускают преобразования, результатом которых может быть исключение цепных, аннулирующих или леворекурсивных правил. Задачу распознавания для КС-языков решают магазинные преобразователи. В общем случае для любой КС-грамматики можно построить магазинный распознаватель, допускающий язык, который порождается заданной грамматикой. Однако, такой распознаватель может оказаться недетерминированным. Работа недетерминированного распознавателя связана с поиском последовательности конфигураций, показывающей допустимость входной цепочки. Поиск увеличивает время работы автомата, поэтому для практических применений предпочитают использовать детерминированные автоматы.Пред.Страница
След.Страница Раздел Содержание
в следующей грамматике, и, если
1) Определите, есть ли бесполезные символы в следующей грамматике, и, если они есть,постройте приведенную грамматикуГ2. 4
: R = {®
| ,
®
a | b | b,
®
| a,
®
| b }.
2) Постройте для заданной грамматики эквивалентную ей неукорачивающую грамматику.
Г2. 5: R = { ®
®
| $ ,
®
| a ,
| b}.
3) Для заданной грамматики постройте эквивалентную грамматику без цепных правил.
Г2. 6: R = { ®
a
,
®
a | ,
®
b | b}
4) По заданной грамматике постройте грамматику без леворекурсивных правил.
Г2. 7 : R = { ®
a ,
®
c ,
®
b ,
®
d }.
5) Проверьте, являются ли цепочки aaabb и aabbaa допускаемыми автоматом М2.
6) Постройте последовательность конфигураций распознавателя М3 для цепочки (a+a) и левый вывод этой цепочки. Сравните содержимое магазина и промежуточные результаты вывода.
7) Постройте магазинные распознаватели для следующих грамматик и проверьте их работу .
а) Г2. 8 : R = { ®
| b , ®
| a}.
б) Г2. 9 : R = { ®
| a , ®
| b , ®
a}.
Пред.Страница
След.Страница Раздел Содержание
Функции ПЕРВ, СЛЕД и множество ВЫБОР
Множество ВЫБОР строится для каждого правила и включает те терминальные символы, при появлении которых под читающей головкой распознаватель должен применять это правило.
Для определения множества ВЫБОР
используются функции ПЕРВ и СЛЕД . Аргументом функции ПЕРВ
может быть любая цепочка полного словаря µ, а значением функции ПЕРВ(µ) является множество терминальных символов, которые могут стоять на первом месте в цепочках, выводимых из цепочки µ.
Пред.Страница
След.Страница Раздел Содержание
Исключение леворекурсивных правил
Возможность построения для LL(1) грамматики детерминированного автомата определяет значение этих грамматик для практических применений. Однако, при построении грамматики для заданного языка не всегда удается получить грамматику, принадлежащую классу LL(1). Это может случиться потому, что неудачно выбраны правила грамматики, или потому, что для заданного языка принципиально нельзя построить LL(1) грамматику. В первом случае полученную грамматику можно попытаться преобразовать таким образом, чтобы она удовлетворяла условиям LL(1) грамматики. Известно несколько приемов преобразований, которые в некоторых случаях, но не всегда, позволяют получить грамматику требуемого вида.
Первый вид преобразований заключается в исключении правил, содержащих левую рекурсию. Необходимость исключения таких правил можно показать с помощью следующих рассуждений.
Допустим, что в схеме заданной грамматики имеются правила:
®
| . Первое условие определения LL(1) грамматики говорит о том, что функции ПЕРВ для правил с одинаковой левой частью не должны иметь одинаковых элементов, но для заданной грамматики это не так, поскольку
ПЕРВ() = ПЕРВ() = ПЕРВ().
Следовательно, грамматика, содержащая рассматриваемые правила, не является LL(1) грамматикой.
Возьмем другие правила, обеспечивающие получение такого же множества цепочек, что и в первом случае : ®
| $.
Первое условие выполняется, но имеем:
СЛЕД ( ) = ПЕРВ () и ПЕРВ () = ПЕРВ (),
поскольку A можно заменить $.
Эти равенства показывают, что нарушается второе условие из определения LL(1) грамматики.
Из приведенных рассуждений можно сделать вывод о том, что LL(1) грамматика не должна содержать леворекурсивных правил. Конечно, лучше не использовать леворекурсивные правила еще на этапе построения грамматики, но если уж они появились, то их можно исключить, пользуясь приемом, описанным в предыдущем разделе.
Пред.Страница
След.Страница Раздел Содержание
LL( - грамматики
Разделенные и слаборазделенные грамматики представляют собой подклассы грамматик более общего вида, которые называются LL(1) грамматиками, и которые определяются следующим образом.
| Определение. КС-грамматика является LL(1) грамматикой тогда и только тогда, когда выполняются следующие два условия: 1 . Для каждого нетерминала, являющегося левой частью нескольких правил: ®a 1 | a 2 | ... | a n, необходимо, чтобы пересечение функций ПЕРВ(a i) и ПЕРВ(a j) было пусто для всех i =/= j. 2 . Для каждого аннулирующего нетерминала ,такого что ==>* $, необходимо, чтобы пересечение множеств ПЕРВ() и СЛЕД() было пустым. |
Из определения следует, что грамматики LL(1), в отличие от разделенных грамматик и слаборазделенных, могут содержать правила, начинающиеся нетерминальными символами. Проверим относится ли рассмотренная ранее грамматика Г43 к классу LL(1).
Для этого необходимо вначале проверить наличие одинаковых значений функций ПЕРВ для правил с одинаковой левой частью. Для правил (1) и (2) имеем
ПЕРВ(
ПЕРВ(
ПЕРВ(g
а для правил (5) и (6) имеем
ПЕРВ(
ПЕРВ(a) = {a,d},
ПЕРВ(ca) = {c}.
Полученные результаты показывают, что первое условие LL(1) грамматики выполняется.
Второе условие необходимо проверить для правил (3) и (7) рассматриваемой грамматики. Вычисляя функции ПЕРВ и СЛЕД для правила (8), имеем:
ПЕРВ() = {b} и СЛЕД() = {a,c,d,g,f}.
Эти функции не имеют одинаковых значений, следовательно грамматика Г43
является грамматикой LL(1).
Рассматриваемый класс грамматик можно определить также с помощью множеств выбора следующим образом:
| Определение . КС-грамматика называется LL(1) грамматикой тогда и только тогда, когда множества ВЫБОР, построенные для правил с одинаковой левой частью, не содержат одинаковых элементов. |
Пред.Страница
След.Страница Раздел Содержание
LR(k)-грамматики
Детерминированные восходящие распознаватели, так же как и нисходящие, могут быть построены не для всякой КС-грамматики, а только для определенных подклассов таких грамматик. Наиболее широким подклассом КС-грамматик являются LR(k)-грамматики. Эти грамматики обеспечивают распознавание цепочки при просмотре слева направо, об этом говорит буква L (Left) в названии грамматики, и позволяют выполнить правостороннее сворачивание, это показывает буква R (Right) в названии. Параметр k говорит о том, что для определения того правила грамматики, которое нужно применить для сворачивания цепочки, потребуется просмотреть не более k еще не прочитанных символов входной цепочки.
В общем случае алгоритмы построения распознавателей дл LR(k)-грамматик оказываются достаточно сложными и трудоемкими, поэтому на практике чаще всего используют подклассы LR(k)-грамматик: LR(0), или SLR(1)—простые (Simple) LR(1)-грамматики, позволяющие относительно просто выполнять построение восходящих распознавателей. При этом для каждого подкласса LR(k)-грамматик используется свой алгоритм построения. Если задана КС-грамматика, то определить ее принадлежность к одному из подклассов грамматик LR(k) можно только путем анализа возможности построения для нее с помощью определенного алгоритма детерминированного распознавателя. Учитывая последнее обстоятельство, условимся называть распознаватели по подклассу соответствующих грамматик: LR(0)-распознаватель или SLR(1)-распознаватель.
Прежде чем перейти к рассмотрению правил построения восходящих распознавателей, введем несколько вспомогательных понятий.
Условимся называть символы полного словаря грамматики грамматическими символами. Каждый грамматический символ может входить в разные правила грамматики и, более того, появляться в одном и том же правиле несколько раз. При этом положение символа в правиле грамматики может показывать, какое действие нужно выполнить: перенос или свертку, а также какие грамматические символы могут за ним следовать.
Это обстоятельство позволяет связать позицию грамматического символа в правиле грамматики с понятием состояния распознавателя. Для удобства дальнейших рассуждений введем понятие грамматического вхождения.
| Определение.Грамматическое вхождение символа грамматики задается номером правила и номером позиции, которая указывает место символа в правой части правила, полагая, что самый левый символ правой части правила является первым. |
Пред.Страница
След.Страница Раздел Содержание
Построение функции СЛЕД()
Аргументом функции СЛЕД является нетерминальный символ, например , а значение функции СЛЕД() представляет собой множество терминалов, которые могут следовать непосредственно за нетерминалом в цепочках, выводимых из начального символа грамматики.Вычисление значения функции СЛЕД() должно выполняться по следующим правилам:
1) Если в схеме грамматики имеются правила вида
µ1a1,
µ2a2, ... ,
® µnan,
и все цепочки a i
=/= $ , то СЛЕД() = ПЕРВ(a
1) И
ПЕРВ(a 2) И
... И
ПЕРВ(a n).
2) Если же среди приведенных выше правил имеется хотя бы одна цепочка ai = $, например пусть a1
= $, то функция вычисляется так: СЛЕД() = СЛЕД(
ПЕРВ(a 2) И
... И
ПЕРВ(a n).
Выполним вычисление функции СЛЕД для нетерминалов грамматики Г3.2
. Вначале определим функцию для нетерминала , который встречается в правой части правила (9).
СЛЕД() = ПЕРВ(f) = {f}.
Нетерминал
ПЕРВ(
Нетерминал входит в правые части правил (1), (2), (5), поэтому имеем: СЛЕД() =ПЕРВ(
СЛЕД() И
СЛЕД(
подставляя в полученное выражение значения функций, входящих в правую часть, получаем: СЛЕД() = { a, c, d, }И
{ f } И
U { c, d, g, } = { a, c, d, g, f }.
Для нетерминала
СЛЕД() И
ПЕРВ(
ПЕРВ(a),
учитывая, что , для нетерминала
СЛЕД(
окончательно имеем:
СЛЕД(
СЛЕД() ИПЕРВ(
{a} =
= {b}И
{f} И
{c,g} И
{a} = {a,b,c,g,f}.
Пред.Страница
След.Страница Раздел Содержание
Построение магазинного автомата
Для грамматик, удовлетворяющих условиям LL(1) грамматик, справедливо следующее утверждение.
| Утверждение. Для каждой LL(1) грамматики Г можно построить детерминированный магазинный автомат М , допускающий язык, порождаемый заданной грамматикой: L ( Г ) = L ( М ). |
Задача построения магазинного автомата для заданной LL(1) грамматики формулируется следующим образом.
Задана грамматика Г = {Vт,Va, I, R}, и требуется определить
об'екты, определяющие автомат М = { P , S , s0
, F , H , h0 , f }.
Учитывая, что автомат должен допускать цепочки языка, порождаемого заданной грамматикой, примем P = Vт. Чтобы упростить описание автомата, допустим, что он имеет одно состояние s0, которое является и начальным и заключительным, то есть - S = {s0}и F = {s0}.
В качестве магазинного алфавита примем следующее объединение: H = {Vт И
Va И
{h0}}.
Построение функции переходов выполним с использованием множеств ВЫБОР правил заданной грамматики следующим образом:
1 ) Для каждого правила грамматики, начинающегося терминальным символом вида
®
b a, построим команду автомата
f ( s0 , b , ) = ( s0
, a
' ) ,
где a
' является зеркальным отображением цепочки
a .
2) Для каждого правила грамматики, начинающегося нетерминальным символом вида
®
a, построим команду автомата f* ( s0 , x , ) = ( s0
, a
' )
где f* - команда автомата без сдвига входной головки, а a
' является зеркальным
отображением цепочки a
.
Количество команд, которые необходимо построить для заданного правила, определяется числом элементов множества ВЫБОР.
Команды магазинного автомата, работающие без сдвига входной головки, выполняют замену нетерминаала, соответствующего левой части правила, цепочкой, соответствующей правой части этого правила. В этом случае сопоставление терминального символа, получаемого при выводе, и очередного символа входной цепочки не производится, поэтому для таких команд сдвиг входной головки не нужен.
3) Для каждого аннулирующего правила грамматики вида
® $
построим команды автомата
f* ( s0 , x , ) = ( s0
, $ )
для каждого элемента x из множества ВЫБОР(
® $). Количество таких команд определяется числом элементов множества ВЫБОР.
4) Для каждого терминального символа b, расположенного в середине или на конце правых
частей правил грамматики, построим команду
f ( s0 , b , b ) = ( s0
, $ ).
5) Для перехода в заключительное состояние построим команду
f* ( s0 , e
, h0 ) = ( s0 , $ , $ ).
В качестве начальной конфигурации автомата условимся использовать следующее выражение с заданной входной цепочкой µ :
(s0,µ,h0).
Пользуясь приведенными правилами, построим магазинный автомат для грамматики Г12, схема которой в символических обозначениях может быть записана так
Г3. 5
: R = {
® x | (),
®
® +
| $}.
Вначале построим множества ВЫБОР для каждого из правил и проверим, является ли эта грамматика LL(1) грамматикой. (1) ВЫБОР( ®x) = ПЕРВ(x) = {x}
(2) ВЫБОР( ®
(())) = ПЕРВ(()) = {(}
Построение множества ВЫБОР
Множество ВЫБОР, которое потребуется нам для построения переходов магазинных автоматов,можно определить с помощью функций ПЕРВ и СЛЕД следующим образом: 1) Если правило грамматики имеет вид- > a и
a не является аннулирующей цепочкой, другими словами не существует вывод a
==>*$, то
ВЫБОР( ®
a ) = ПЕРВ( a ).
2) Для аннулирующих правил грамматики вида ®$, мно-
жество выбора определяется так
ВЫБОР(
® $) = СЛЕД().
3) Если правило грамматики имеет вид ® µ и µ
яв-
ляется аннулирующей цепочкой, то
ВЫБОР(
® µ) = ПЕРВ(µ) И
СЛЕД().
Для рассматриваемой грамматики Г3.2 множества ВЫБОР для каждого из правил, построенные описанным выше способом, имеют вид:
ВЫБОР( ®
ВЫБОР( ®
g
ВЫБОР( ®
$) = ПЕРВ($) И
СЛЕД() = {a,c,d,g,f},
ВЫБОР( ®
b
ВЫБОР(
ВЫБОР(
ca) = ПЕРВ(ca) = {a},
ВЫБОР(
$) = ПЕРВ($) И
СЛЕД(
ВЫБОР(
d
ВЫБОР(
gf) = ПЕРВ(gf) = {g},
ВЫБОР(
c) = ПЕРВ(c) = {c}.
Пред.Страница
След.Страница Раздел Содержание
Преобразование грамматик к виду LL(
Пример работы расширенного магазинный автомат
В качестве иллюстрации работы расширенного автомата рассмотрим автомат, допускающий язык L={wwR | w О {a, b}*}.
M7.1: P = {a, b}, S = {s0, s1}, H = {a, b, , h0}, F = {s1} ,
d(s0, a, h0) = (s0, h0a), d(s0, a, ) = (s0, a),
d(s0, b, h0) = (s0, h0b), d(s0, b, ) = (s0, b),
d(s0, a, a) = (s0, aa), d*(s0, a, aa) = (s0, ),
d(s0, b, a )= (s0, ba), d*(s0, b, aa) = (s0, ),
d(s0, a, b) = (s0, ab), d*(s0, a, bb) = (s0, ),
d(s0, b, b) = (s0, bb), d*(s0, b, bb) = (s0, ),
d*(s0, a, aa) = (s0, ), d*(s0, $, aa) = (s0, ),
d*(s0, b, aa) = (s0, ), d*(s0, $, bb) = (s0, ),
d*(s0, a, bb) = (s0, ), d*(s0, $, h0) = (s1, $).
d*(s0, b, bb) = (s0, ),
Это недетерминированный автомат. Если на входе задана цепочка abba, то его работу можно представить в виде следующего ряда конфигураций:
| № | Вход | Магазин | Состояние | ||||
| 1. | abba|- | h0 | s0 | ||||
| 2. | bba|- | h0a | s0 | ||||
| 3. | ba|- | h0ab | s0 | ||||
| 4. | a|- | h0abb | s0 | ||||
| 5. | a|- | h0a | s0 | ||||
| 6. | |- | h0aa | s0 | ||||
| 7. | |- | h0 | s1 |
Пред.Страница
След.Страница Раздел Содержание
Распознаватели и LL(K) - грамматики
Моделирование работы недетерминированных магазинныхраспознавателей связано с поиском последовательности переходов из начального в одно из конечных состояний. Поиск состоит из отдельных шагов, каждый из которых может окончиться неудачно и привести к возврату в исходное состояние для выполнения следующего шага. Такой поиск с возвратом связан со значительными затратами времени, поэтому на практике используют более экономичные детерминированные распознаватели, работающие без возвратов. Эти распознаватели допускают только ограниченные классы КС-языков, которые однако отражают все синтаксические черты языков программирования.
Распознаватели можно разделить на две категории: нисходящие и восходящие. Каждая категория характеризуется порядком, в котором располагаются правила в дереве вывода. Нисходящие распознаватели обрабатывают правила сверху вниз, верхние правила раньше нижних, в то время как восходящие анализаторы используют нижние правила раньше тех, что расположены выше. Чтобы показать возможности детерминированных автоматов и способы их построения, в настоящем разделе рассматриваются нисходящие распознаватели, допускающие языки, порождаемые грамматиками вида LL(K).
| Определение. В общем случае грамматика относится к классу LL(K) грамматик, если для нее можно построить нисходящий детерминированный распознаватель, учитывающий K входных символов, расположенных справа от текущей входной позиции. |
Название LL произошло от слова Left, поскольку анализатор просматривает входную цепочку слева-направо , и слова Leftmost, поскольку он обнаруживает появление правила по одному или группе символов, образующих левый край цепочки. На практике наибольшее применение имеет класс LL(1) грамматик, для которых детерминированный распознаватель работает по дному входному символу, расположенному в текущей позиции. В качестве первого шага изучения нисходящих распознавателей рассмотрим их построение для одного из подклассов LL(1) грамматик.
Пред.Страница
След.Страница Раздел Содержание
Распознавателя
Способ построения распознавателя предусматривает сопоставление каждому правилу грамматики команды распознавателя .
Согласно общему способу построения распознавателей для КС-грамматик, описанному в предыдущем разделе, каждому правилу разделенной грамматики, которые имеют вид:
® a a , где a
- цепочка символов полного словаря и a принадлежит
терминальному словарю, нужно поставить в соответствие команду
(*) f 0( s0 , e , ) = ( s0
, a
' a) ,
которая задает такт работы без сдвига входной головки и в которой
a ' представляет собой зеркальное отображение цепочки a
. Отметим, что в результате выполнения этой команды, в вершине магазина окажется терминал a. Общий способ построения редусматривает также построение для каждого a
символа грамматики команды:
(**)
f ( s0 , a , a ) = ( s0 , $ )
которая удаляет этот терминал из магазина и сдвигает входную головку.
Учитывая, что в разделенной грамматике каждое правило начинается с терминального символа, и что эти терминалы не повторяются, можно сделать вывод о том , что команда (*) должна выполняться только в том случае, когда под входной головкой находится терминал
a, и после нее всегда должна выполняться команда (**).
Чтобы исключить неопределенность правил вида (*) и уменьшить число тактов работы распознавателя, объединим команды вида (*) и (**) в одну команду. Построение такой команды должно выполняться следующим образом: каждому правилу разделенной грамматики ® a a
поставим в соответствие команду
f ( s0 , a , ) = ( s0 , a
') ,
которая определяет такт работы распознавателя со сдвигом входной головки.
Кроме того, следует учесть, что терминальные символы могут быть расположены в правых частях правил не только на самой левой позиции. Для таких терминалов необходимо построить команды вида :
f ( s0 , b , b ) = ( s0
, $ )
Для перехода в заключительное состояние добавим правило:
f ( s0 , $ ,h0 ) = ( s1 , $ ) ,
а в качестве начальной конфигурации распознавателя примем, как
обычно, следующее выражение :
( s0 , a
, h0 ) ,
где - начальный символ грамматики, а a - заданная входная цепочка.
Применяя приведенные выше правила, построим распознаватель для разделенной грамматики
Г3. 0
. В результате получаем: М 4 : P = { a , b }, H = { a , b , , , h0 }, S = {s0}, F= {s0},
f ( s0 , a , ) = ( s0
, b )
f ( s0 , a , ) = ( s0
, $ )
f ( s0 , b , ) = ( s0
, b )
f ( s0 , b , ) = ( s0
, )
f ( s0 , b , b ) = ( s0
, $ )
f ( s0 , e
, h0 ) = ( s0 , $ )
Работу построенного автомата покажем на примере анализа цепочки bbabab.
( s0 , bbababa , h0 ) |---
( s0 , bababa , h0b ) |---
( s0 , ababa , h0b ) |---
( s0 , baba , h0b ) |---
( s0 , aba , h0 ) |---
( s0 , ba , h0b ) |---
( s0 , a , h0 )
|--- ( s0 , $ , h0
) |--- ( s0 , $ , $ ) .
Приведенная последовательность конфигураций показывает, что в каждой конфигурации может быть применена единственная команда детерминированного распознавателя.
Пред.Страница
След.Страница Раздел Содержание
Расширенный магазинный автомат
Рассмотренный пример показывает, что автомат, выполняющий операцию свертки, в отличие от нисходящего распознавателя, не строит в магазине вывод цепочки, начиная с аксиомы грамматики, который соответствует построению синтаксического дерева цепочки "сверху - вниз", а выполняет сворачивание символов, записанных в магазин. Такой порядок сворачивания символов, записанных в магазин, соответствует правому выводу цепочки, выполняемому "снизу - вверх". Это обстоятельство объясняет, почему такие распознаватели называются восходящими. Подобный распознаватель должен учитывать при переходе не один символ, расположенный в вершине магазина, а цепочку символов. Чтобы устранить отмеченное противоречие, определим новый тип автомата, который назовем расширенным магазиннным автоматом.
| Определение. Формальное определение такого автомата имеет вид: M = {P, S, H, F, s0, h0, d}, где P - входной алфавит, S - алфавит состояний, s0- начальное состояние , s0 ОS, F - множество конечных состояний, F является подмножеством S, H - алфавит магазинных сисмволов, записываемых на вспомогательную ленту, h0 - маркер дна, он всегда записывается на дно магазина, h0 О H, d: S * {P И {$}} * H* ® S*H* - функция переходов. |
В функциональном виде функции переходов расширенного автомата можно записать так: d(s, p, ga) = (s, gb),
где a, b, g О
H*, p О (P И
{$}) и s О S.
Приведенное определение показывает, что расширенный автомат допускает замену одной цепочки, находящейся в вершине автомата, другой цепочкой.
Используя введенное ранее определение конфигурации автомата, работу расширенного магазинного автомата можно представить в виде последовательности сменяющих друг друга конфигураций.
При этом начальная и конечная конфигурации имеют вид:
(s0, a,р
h0 ) и (s1, $, h0I ),
где a - заданная цепочка, s1 - одно из заключительных состояний автомата, I - начальная аксиома грамматики.
Цепочку и язык, допускаемые расширенным автоматом, можно определить так.
| Определение. Цепочка допускается расширенным автоматом, если существует последовательность конфигураций, первая из которых является начальной конфигурацией с заданной цепочкой, а последней конфигурацией в последовательности является одна из заключительных конфигураций. ( s0, a,р h0 ) , $|--* ( s1, h0I ), где s1 - одно из заключительных состояний, a - заданная цепочка. Определение. Язык, допускаемый расширенным автоматом, можно определить так: L(M) = { a | (s0, a,р h0 ) |--* ( s1, $,$ ) и s1ОF}. |
с помощью правого вывода, можно
Пред.СтраницаСлед.Страница Раздел Содержание
 3.15. Резюме.
3.15. Резюме.Каждую цепочку, построенную с помощью правого вывода, можно преобразовать в начальный символ грамматики, последовательно заменяя правые части правил, выделенные в цепочки, левыми частями. Такая операция замены, являющаяся обратной по отношению к операции вывода, называется сворачиванием или сверткой. Восходящий распознаватель работает, последовательно выполняя операции переноса и свертки. Вначале он переносит символы входной цепочки в магазин до тех пор, пока в магазине не образуется правая часть какого-либо правила, а затем он выполняет операцию сворачивания.Формальной моделью восходящего распознавателя является расширенный автомат, допускающий, в отличие от простого автомата, при переходе чтение цепочки, находящейся в вершине магазина.
Детерминированные восходящие распознаватели могут быть построены для LR(k) грамматик, которые являются подклассом контекстно-свободных грамматик. Процедура построения LR(k)-распознавателя оказывается весьма сложной и трудоемкой, поэтому в настоящем пособии рассматриваются грамматики LR(0) и SLR(1), которые включаются в подкласс LR(1) грамматик. Подкласс грамматик SLR(1) грамматик является достаточно широким. Кроме грамматик LR(0) он включает грамматики LL(1) и грамматики слабого предшествования. Диаграмма включения подклассов LR(1) грамматики приведена на рис.3.1.
Принадлежность к подклассу LR(0) или SLR(1) грамматик устанавливается путем проверки возможности построения соответствующего распознавателя. Процедура построения восходящих распознавателей состоит из двух частей: построение таблицы переходов и построение таблицы действий. Первая часть этой процедуры оказывается одинаковой для преобразователей LR(0) и SLR(1). Отличия в процедуре построения проявляются во второй части.
LR(1)
|
|
------------------SLR(1)----------------
| | |
| | |
LR(0) со слабым LL(1)
предшествованием
Рис. 3.1
Слаборазделенные грамматики
Используя введенные понятия, можно дать определение слаборазделенной грамматики.
| Определение. КС-грамматика называется слаборазделенной, если выполняются следующие три условия: правая часть каждого правила представляет собой либо пустую цепочку $, либо начинается с терминального символа, если два правила имеют одинаковые левые части, то правые части правил должны начинаться разными символами, для каждого нетерминала A, такого что A ==>* $ множество начальных символов не должно пересекаться с множеством символов, следующих за A.: ПЕРВ(A) З СЛЕД(A) = $ |
Используя приведенное определение, выясним, является ли следующая грамматика слаборазделенной:
Г3. 3
: R = {(1) ®
a , (2) ®
b ,
(3) ®
ca ,
(4) ®
$ }.
Эта грамматика не содержит правил с одинаковой левой частью, начинающихся одинаковыми терминалами, поэтому нужно проверить только условие (3) для правила (4). Вычисляя функции
ПЕРВ() = {c} и СЛЕД() = СЛЕД() = {a},
находим, что множество значений функции ПЕРВ() и множество значений функции СЛЕД() не имеют общих элементов. Следовательно, грамматика Г3.3 является слаборазделенной.
Проверка выполнения условия (3) для грамматики
Г3. 4: R = { ®
a | $ ,
® a | b }
дает следующие результаты:
ПЕРВ() = {a} и СЛЕД() = ПЕРВ() = {a,b},
которые показывают, что пересечение множеств ПЕРВ() и СЛЕД() не пусто. Следовательно грамматика Г3.4
не является слаборазделенной.
Пред.Страница
След.Страница Раздел Содержание
Определить какие из следующих грамматик,
1) Определить какие из следующих грамматик, заданных схемами, относятся к классу LL(1) грамматик.а) Г3. 6 : R = {
® a,
®
b,
®
c,
®
$}.
б) Г3. 7 : R = {
® a,
®
$,
®
b,
®
$}.
2) Проверить принадлежность к классу LL(1) и построить распознаватель для следующих грамматик:
а) Г3. 8 : R = {
® a,
®
b,
®c,
®
d}
б) Г3. 9 : R = {
® a,
®
(),
®
a,
®
$}.
в) Г3. 10
: R = { ® b,
®
d,
®
b,
®
,
®
cd,
®
$,
a,
ed}
Пред.Страница
След.Страница Раздел Содержание
1) Постройте LR(0)–распознаватели для следующих грамматик:
a)
® (
® a
б)
®
=
®
2) Постройте SLR(1) преобразователи для следующих грамматик:
а)
® ab
® ab
б)
®
® a
®
® b
® a
в)
® (
® ,a
® $
® $
3) Показать, что следующая грамматика не входит в подкласс SLR(1)–грамматик.
®
ab
®
ba
®
$
Пред.Страница
След.Страница Раздел Содержание
Восходящие распознаватели
В основе работы восходящего распознавателя лежит операция сворачивания или свертки, которая применяется к цепочке, полученной с помощью правого вывода. Эта операция является противоположной выводу. Она заключается в том, что правая часть правила заменяется левой частью. При работе входящий распознаватель переносит символы входной цепочки в магазин и, когда в магазине оказывается правая часть какого-либо правила, осуществляет операцию свертки. Эту операцию можно определить следующим образом.
| Определение. Пусть задана грамматика Г, в схеме которой имеется правило r =A®y и задана цепочка g = r1A r2. Если правая часть цепочки правила r является частью цепочки , то можно получить цепочку t = r1y r2 , заменяя правую часть правила грамматики левой частью. В этом случае говорят, что цепочка tt получается путем непосредственного сворачивания цепочки g и используют обозначение t <= g . Определение. Если существует множество цепочек W = ( w1, w2, ...wn ), таких, что w1 Ь w2 , w2 Ь w3 , ... , wn-1Ь wn , то говорят, что цепочка wn сворачивается в цепочку w1 и используют обозначение w1 *Ь wn . |
Задача распознавания принадлежности данной цепочки языку, порождаемому грамматикой Г, может быть сформулирована следующим образом. Если из заданной цепочки с помощью операции сворачивания можно получить начальный символ грамматики, то такая цепочка может быть построена с помощью правил заданной грамматики, и, следовательно, она принадлежит языку, порождаемому этой грамматикой.
Например, сворачивание цепочки, полученной с помощью правого вывода и правил следующей грамматики
Г3. 11
:
(1) ®
a,
(2) ®
(
(3)
,
(4)
).
можно представить так: (a,a) Ь 1 (,a) Ь 1 (,) Ь 4
(,
Каждый шаг рассмотренной процедуры связан с выделением в цепочке правой части какого-либо правила и заменой его левой частью правила. В последовательности сворачиваний правые части правил называются основой
рассматриваемой цепочки. В общем случае основу можно определить так:
| Определение. Основой цепочки называют вхождение правой части последнего правила, примененного при правом выводе рассматриваемой цепочки. |
| 1. h0 | (a,a)^ | Перенос |
| 2. h0( | a,a)^ | Перенос |
| 3. h0(a | ,a)^ | Свертка(1) |
| 4. h0( | ,a)^ | Перенос |
| 5. h0(, | a)^ | Перенос |
| 6. h0(,a | )^ | Свертка(1) |
| 7. h0(, | )^ | Перенос |
| 8. h0(,) | ^ | Свертка(4) |
| 9. h0(, |
^ | Свертка(3) |
| 10. h0( |
^ | Свертка(2) |
| 11. h0 | ^ | Допустить |
Пред.Страница
След.Страница Раздел Содержание
Выделение общих частей
Второй вид преобразований, который называют выделением общих частей, применяют для устранения правил с одинаковыми левыми частями, правые части которых начинаются одинаковыми последовательностями символов.
Например, рассмотрим грамматику с правилами
® a,
® a.
Эта грамматика не является LL(1) грамматикой, т.к. значения функций ПЕРВ(a) и ПЕРВ(a) совпадают. Введем дополнительный нетерминал A и преобразуем грамматику так:
® a,
®
|$.
В этой грамматике отсутствуют правила с одинаковой левой частью, поэтому для нее выполняется первое условие определения LL(1) грамматики. В общем случае, если заданная грамматика содержит правила
® a
µ1 | a µ2 | ... | a
µn ,
то, вводя дополнительный нетерминал
® a
® µ1
| µ2 | ... | µn.
Полученные правила могут быть использованы для построения LL(1) грамматики.
Покажем возможность применения этого вида преобразования на следующем примере. Пусть дана грамматика .
Г3. 6: R = { ®
b, ®
b,
® dca,
® f,
®ca,
® c }.
Эта грамматика не является LL(1) грамматикой, поскольку нарушено первое условие. Воспользуемся способом выделения общих частей: введем нетерминалы D, E и построим правила:
®
| $
® a | $ .
В результате включения этих правил в схему грамматики получаем:
® b
$
®
dca
®
f
®
c
a
$
Для этой грамматики первое условие принадлежности грамматики к классу LL(1) выполняется.
Чтобы проверить второе условие, найдем функции ПЕРВ и СЛЕД для аннулирующих правил. СЛЕД(
ПЕРВ(ca) = {c},
ПЕРВ(
СЛЕД(
ПЕРВ(
Полученные значения показывают, что второе условие выполняется, и что построенная грамматика является грамматикой типа LL(1).
Преобразование для грамматики Г 3. 6 закончилось удачно, но так бывает не всегда. Часто исключение правил, нарушающих первое условие, приводит к появлению аннулирующих правил, для которых нарушается второе условие.
Третий вид преобразования предполагает исключение аннулирующих правил и построение неукорачивающей грамматики. Такие преобразования могут оказаться полезными, если нарушается второе условие принадлежности грамматики к классу LL(1).
Пред.Страница
След.Страница Раздел Содержание
Магазинные Преобразователи
Магазинные автоматы, рассмотренные в предыдущем разделе, позволяют определить для цепочки, заданной на входе, ее принадлежность к языку, допускаемому автоматом. Настоящий раздел посвящен другому типу моделей устройств, называемому магазинными преобразователями. Подобные устройства позваляют строить по заданной входной цепочки соответствующую ей выходную цепочку. Множество таких пар цепочек называют переводом или трансляцией, допускаемым магазинным преобразователем. Для того чтобы построить преобразователь необходимо заранее знать какой перевод он должен выполнять. Кроме того, преобразователь можно построить не для любого перевода, а только для такого, который может быть описан с помощью простой СУ-схемы. Для построения детерминированного преобразователя необходимо еще, чтобы входная грамматика заданной СУ-схемы пораждала детерминированный язык.
Пред.Страница След.страница Раздел Содержание
Описание работы магазинного преобразователя
Для описания работы магазинного преобразователя необходимо дать его определение.
| Определение: Преобразователем с магазинной памятью (Мп) называется совокупность восьми объектов: Мп={P, S, s0, H, h0, F, W, q}, где P - входной алфавит, состоящий из символов, записываемых на входную ленту; W - выходной алфавит, содержащий символы, записываемые на выходную ленту; H - магазинный алфавит, содержащий символы, записываемые и считываемые из магазина; h0 - маркер дна магазина, он принадлежит H; S - множество состояний преобразователя; s0- начальное состояние из множества S; F - множество конечных состояний, представляющих собой подмножество S; j - функция переходов преобразователя, которая задает отображение, j: Sx{P И {$} x H Ю S x H* x W* . Она может быть записана в функциональном виде: j(s, p, h) = (s', b, e), где h О H, p О P, b О H*, e О W* и s,s' О S. |
Определим конфигурацию Мп как четверку
(s, ac, rh, d),
где ac
О P*, rh
О H*
и d
О W*.
Если такту работы преобразователя соответствует конфигурация (s, ac, rh , d) и определена функция переходов j(s, a, h) = (s', b, e), то происходит смена конфигурации, которую условимся записывать так:
(s, ac,
rh, d) |-- (s', c, rb,
de).
Последовательность сменяющих друг друга конфигураций, как обычно, обозначим символом |--*. В качестве начальной примем конфигурацию, которой соответствует заданная входная цепочка c
на ленте, цепочка h0I в магазине, начальное состояние s0
и пустая цепочка на выходной ленте:
(s0, c, h0I, $).
Конечной или заключительной конфигурацией назовем четверку (sk, $, $, d), где sk
- одно из заключительных состояний из множества F, а d
- выходная цепочка.
Пред.СтраницаСлед.Страница
Определение магазинного преобразователя
.Магазинный преобразователь (Мп)
от магазинного автомата наличием дополнительной выходной ленты, на которую записывается выходная цепочка. Схему магазинного преобразователя
можно изобразить следующим образом:
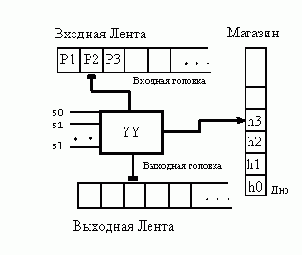
В этой схеме входная головка в каждом такте работы может оставаться на месте или двигаться на одну позицию вправо. Выходная головка также может быть неподвижной или смещаться вправо, а головка магазинной ленты может перемещаться в обоих направлениях, причем такие перемещения связаны с операциями записи и чтения.
Пред.Страница След.Страница Раздел Содержание
Перевод определяемый преобразователем
| Определение. Цепочку d назовем выходом для цепочки c, если существует последовательность конфигураций, первой из которых является начальная конфигурация с заданной входной цепочкой c, а последней – заключительная конфигурация с выходной цепочкой d: (s0, c, h0I, $) |--* (s', $', $, d). Определение. Переводом, определяемым преобразователем с магазинной памятью Мп, назовем множество пар, состоящих из входных и соответствующих им выходных цепочек. D(Mп) = {(x, y) | (s0, c, h0, $) |--* (s', $', $, y) & s' О F} |
Используя последнее определение, можно определить возможность построения преобразователя, реализующего заданный перевод в виде следующего утверждения.
| Утверждение. Для каждой простой СУ-схемы перевода Т = {Va, Vтвх, Vтвых, Q, I} можно построить такой Мп магазинный преобразователь, что D(Т) = D(Мп). |
| Утверждение. Для каждой простой СУ - схемы перевода Т, входная грамматика которой принадлежит классу LL(1) - грамматик, можно построить такой детерминированный магазинный преобразователь Мп, что перевод, определяемый преобразователем, совпадает с переводом, задаваемым СУ - схемой Т. |
Порядок построения детерминированного магазинного преобразователя
В общем случае, если заданы входной и выходной языки, то порядок построения детерминированного магазинного преобразователя можно представить следующим образом:
Построить грамматику, описывающую цепочки входного языка.
Проверить принадлежность этой грамматики классу LL(1)- грамматик. Если условия LL(1) - грамматики не выполняются, то попытаться выполнить преобразование или вернуться к п.1 и построить другую грамматику.
Построить простую СУ-схему, используя построенную грамматику в качестве входной грамматики СУ - схемы.
Построить транслирующую грамматику для полученной СУ -схемы.
Используя правила построения, найти команды преобразования для разных групп правил транслирующей грамматики.
Убедиться, что построенный преобразователь реализует заданный перевод, выполняя несколько примеров построения выходных цепочек с помощью команд преобразователя.
Пред.СтраницаСлед.Страница Раздел Содержание
Построение преобразователя
Покажем теперь, как по заданной СУ - схеме можно построить детерминированный преобразователь. В начале по заданной СУ - схеме построим транслирующую грамматику Г. Это всегда можно сделать, поскольку заданная СУ - схема должна быть простой. Если входная грамматика заданной СУ - схемы относится к классу LL(1) -грамматик, то и входная грамматика транслирующей грамматики также должна относиться к этому классу, поскольку при построении Т - грамматики входные правила изменениям не подвергались. Учитывая, что искомый преобразователь должен в процессе формирования выхода осуществлять и распознавание входной цепочки, будем его строить по правилам транслирующей грамматики, используя правила построения распознавателя.
Такой преобразователь должен воспроизводить левый вывод входной цепочки в магазине и удалять терминальные символы, на ходящиеся в вершине, при совпадении их с очередным символом на входной ленте. Однако при этом в магазин будут записываться выходные символы, содержащиеся в правилах Т - грамматики, и возникнут неопределенные ситуации при появлении выходного символа в вершине магазина. Чтобы исключить такие ситуации, дополним этот правила построения преобразователя следующим правилом: при появлении выходного символа в вершине магазина он должен передаваться на выход независимо от того, какой символ находится под входной головкой.
Построение функции переходов МП
(1) Для всех правил вида
--> ba, где b О
Vтвх и a О(Vтвх
U Vтвых U Va)*, строим ко-
манды:
j( s0, b, A)=( s0, a', $ ),
где a' - зеркальное отображение цепочки a.
(2) Для всех правил вида
--> a, где B ОVa и a О(Vтвх
U Vтвых U Va)*, строим коман-
ды:
j*( s0, u, A ) = ( s0, aB , $ ),
где u О ВЫБОР( --> aвх) и aвх - цепочка, полученная из a путем удаления из
нее всех выходных символов.
. (3) Для всех правил вида
--> $ строим команды:
j*( s0, u, A ) = ( s0, $, $ ),
где u О
ВЫБОР( --> $).
(4) Для всех символов b, принадлежащих, Vтвх , стоящих на первом месте в правой части правил
транслирующей грамматики, т.е. символов,заносимых в магазин, строим правило:
j( s0, b, b ) = ( s0, $, $ ).
(5) Для всех выходных символов {u}, таких что u О Vтвых U {$}, строим команды:
j*( s0, z, {u} ) = ( s0, $, {u} ),
где z О
Vтвх.
Точнее команды строятся для сочетаний {u}z, таких что z может следовать за {u} в цепочках,
выводимых в за данной грамматике.
(6) Заключительное правило строим так:
j( s0, $, h0 ) = ( s0, $, $ ).
Пред.СтраницаСлед.Страница Раздел Содержание
Построение восходящих преобразователей
Пред.СтраницаСлед.СтраницаРаздел Содержание4.3.7 Построение восходящих преобразователей.
Построение восходящих преобразователей, так же как в рассмотренном выше случае, выполняется на основе распознавателя путем модификации команд за счет выполнения операции передачи выходных символов. Одно из отличий построения восходящих преобразователей заключается в том, что для их построения должна быть использована транслирующая грамматика в постфиксной форме.
| Определение. Транслирующая грамматика, записанная в форме, когда все символы действия в правых частях распо ложены правее всех терминальных и нетерминальных символов, называется постфиксной транслирующей грамматикой. |
Это определение говорит о том, что правила постфиксной транслирующей грамматики должны иметь вид:
®
a{ z },
где a О( VT И VА) * и z О VTвых
.
Любая транслирующая грамматика может быть преобразована в постфиксную форму путем разбиения правил грамматики и добавления новых нетерминальных символов. Например, для преобразования правила
® a{ z }{ w },
введем дополнительный нетерминал и разобьем исходное правило на две части. В результате получаем правило в постфиксной форме:
®
Воспользуемся этим приемом для преобразования к постфиксной форме транслирующей грамматики, которая задает преобразование арифметических выражений без скобок, описываемых грамматикой 4. 2, в постфиксную форму.
Г 4. 2 : ® a{a}
Добавляем три новых нетерминала ,
,и, разбивая правила грамматики, получаем грамматику в постфиксной форме.
Г 4. 3 : ®,
® a{a},
® ,
® +a{a}{+},
® ,
® -a{a}{-},
® $.
Напомним, что при построении восходящих распознавателей обработка каждого правила A
® ax
с номером k с символом x, занимающим самую правую позицию в правой части правила, связывалась операция Свертка(k). В постфиксной транслирующей грамматике самую правую позицию могут занимать символы действия, поэтому при построении восходящего преобразователя эти символы можно объединить с операцией свертки в одну операцию, которую назовем
Свертка - Действие(k) (СД(k)). Учитывая, что все символы действия постфиксной транслирующей грамматики могут быть объединены с операциями свертки, приходим к заключению, что процедура построения восходящего распознавателя может быть применена для построения восходящего преобразователя при условии, что вместо операции Cвертка (k) будет использоваться операция Свертка - Действие(k) для правил построения постфиксной транслирующей грамматики, содержащая символы действия.
В качестве иллюстрации последнего утверждения рассмотрим построение преобразователя для грамматики Г 4. 3. Выполняя последовательно шаги процедуры построения SLR(1) преобразова-
теля для грамматики с аннулирующими правилами и заменяя операции Свертка(k) для правил 2, 4 и 6 операциями Свертка - Действие(k), получаем таблицы переходов и действий искомого преобразователя в следующем виде.
Таблица 4.1<
I S R P Q + - a I0 S R1 P Q + - R1 a2 P R3 P Q + - R3 + a4 a4 Q R5 P Q + - R5 - a6 a6 h0 I0 S a2
Таблица 4.2
В качестве демонстрации работы преобразователя построим последовательность конфигураций для входной цепочки а + а - а|--, дополнив эту последовательность указателем выполняемого действия.
+ - a |-- I0 D S П П c7 R1 c1 c1 CD2 CD2 CD2 P П П c7 R3 c3 + П a4 CD4 CD4 CD4 Q П П c7 R5 c5 - П a6 CD6 CD6 CD6 a4 П
Вход Магазин Действие Выход
1. а + а - а|-- h0 П -
2. + а - а|-- h0 a2 СД2 a
3. + а - а|-- h0 S П a
4. а - а|-- h0 S + П a
5. - а|-- h0 S + a4 СД4 aa +
6. - а|-- h0 S P П aa +
7. а|-- h0 S P- П aa +
8. |-- h0 S P - a6 СД6 aa + a -
9. |-- h0 S P Q С7 aa + a -
10. |-- h0 S P Q R5 С5 aa + a -
11. |-- h0 S PR3 С3 aa + a -
12. |-- h0 S R1 С1 aa + a -
13. |-- h0 I0 Д aa + a -
Приведенная последовательность конфигураций показывает, что выходная цепочка формируется при выполнении операций СД2, СД4 и СД6 соответственно на 2, 5 и 8 шаге.
Пред.Страница След.Страница Раздел Содержание
Пример построения преобразователя
Применение правил построения команд преобразователя рассмотрим на примере транслирующей грамматики Г, которая описывает перевод инфиксных выражений, состоящих из идентификаторов и знаков + и *, в постфиксные польские выражения. Эта грамматика имеет следующую схему:
Г 4. 1 : R = {
Используя правило построения команд преобразователя (1) для правил грамматики, начинающихся входным терминальным символом, получаем команды преобразователя Мп1:
q(s0, +,
q(s0, *,
q(s0, a,
Правила построения команд вида (2),(3),(4) к заданной грамматике неприменимы, поэтому с помощью правил вида (5) построим команды, обеспечивающие передачу выходных символов на выход. Эти команды имеют вид:
q*(s0, +, {+}) = (s0, $, +), q*(s0, *, {+}) = (s0, $, +),
q*(s0, a, {+}) = (s0, $, +), q*(s0, $', {+}) = (s0, $, +),
q*(s0, *, {*}) = (s0, $, *), q*(s0, +, {*}) = (s0, $, *),
q*(s0, *, {a}) = (s0, $, *), q*(s0, $', {*}) = (s0, $, *),
q*(s0, a, {a}) = (s0, $, a), q*(s0, +{a}) = (s0, $, a),
q*(s0, *, {a}) = (s0, $, a), q*(s0, $', {a}) = (s0, $, a)
Для перехода в заключительное состояние s1
в соответствии с правилом (6) построим команду:
q(s0, $', h0) = (s1, $, $)
Чтобы посмотреть как работает построенный преобразователь, рассмотрим построение выходной цепочки для входа +a*aa. Последовательность конфигураций, получаемых с помощью команд преобразователя имеет вид:
(s0, +a*aa, h0E, $) |-- (s0, a*aah0{+}EE, $) |--
(s0, *aa, h0{+}T{a}, $) |--
(s0, *aa, h0{+}E, a) |--
(s0, aa, h0{+}{*}T{a}, a) |--
(s0, a, h0{+}{*}E, aa) |--
(s0, $, h0{+}{*}{a}, aa) |--
(s0, $, h0{+}{*}, aaa) |--
(s0, $, h0{+}, aaa*) |--
(s0, $, h0, aaa*+) |--
(s0, $, $, aaa*+).
Результатом работы преобразователя
является выходная цепочка aaa*+, представляющая постфиксную запись заданной входной цепочки.
Пред.СтраницаСлед.Страница Раздел Содержание
АСИНХРОННЫЙ S-ТРИГГЕР
Основные типы асинхронных триггеров строятся, как правило, на основе триггера типа R-S. Метод их построения рассмотрим на примере S-триггера. Обозначим буквами S и R входы создаваемого S-триггера, а функции возбуждения R-S-триггера, используемого в качестве элемента памяти, обозначим символами q’R и q’S. Вначале построим таблицу переходов S-триггера, исходя из его реакции на входные сигналы (рис. 11,а ). Затем построим таблицы функций возбуждения q’R и q’S
триггера R-S, который используется в качестве основного элемента памяти (рис. 11,б ).

Особенностью рассмотренных триггеров является то, что изменение их состояния начинается одновременно с подачей входного сигнала, поэтому реализация асинхронных триггеров типа T и J-K оказывается невозможной.
Пред.Страница
След.Страница Раздел Содержание
АСИНХРОННЫЙ ТРИГГЕР J-K С ЗАДЕРЖКОЙ
На выходе асинхронного триггера с задержкой изменение сигнала может произойти только после окончания действия входного сигнала х, звавшего такое изменение. Если после сигнала х подать сигнал, вызывающий переход в первоначальное состояние, то ожидаемое изменене сигнала на выходе может не произойти: выходной сигнал будет потерян. Чтобы избежать подобных ситуаций, на практике вводят ограничения на последовательности сигналов, подаваемых на вход триггера. Например, для асинхронного триггера J-K последовательности 11 01, 10 01, 01 10, 11 10 являются запрещенными, поскольку каждая из них приводит к потере выходного сигнала. Рассмотрим, как реагирует триггер на одну из эти х последовательностей. Пусть триггер находится в состоянии 0, которому соответствует выходной сигнал 0, и на вход поступает сигнал 11. Под действием этого сигнала триггер должен перейти в состояние, отмеченное выходным сигналом 1. Если же после 11 на вход подать сигнал 01, то триггер вернется в состояние 0 и выходной сигнал, соответствующий входному сигналу 11, окажется потеренным.
Диаграмма и таблица переходов асинхронного J-K-триггера с задержкой, построенные с учетом перечисленных ограничений, приведены на рис. 17. Таблицы функций возбуждения R-S-триггеров изображены на рис. 18, а схема триггера - на рис. 19.
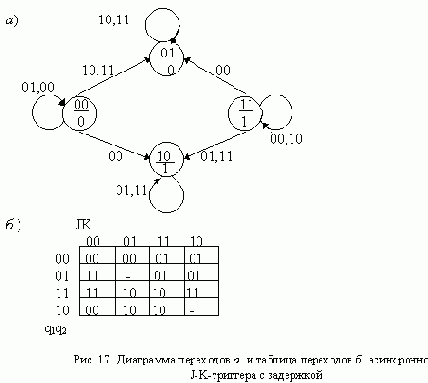
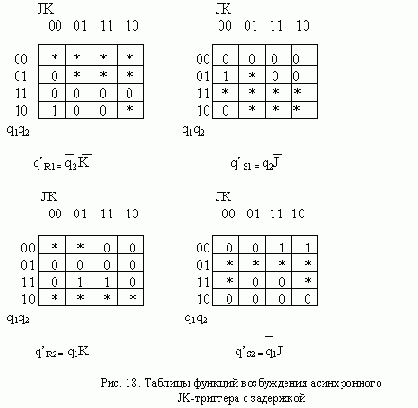
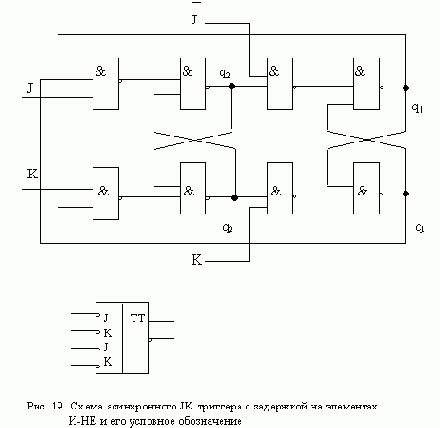
Пред.Страница
След.Страница Раздел Содержание
АСИНХРОННЫЙ ТРИГГЕР
На входе обычного триггера, построенного из элементов потенциального типа, подаются потенциальные сигналы, поэтому его назвают асинхронным триггером. Такие триггеры строят как обыкновенные асинхронные автоматы, используя в качестве элемента памяти асинхронный триггер типа R-S. В отличие от всех остальных триггеров построение R-S-триггера производится по характеристическому уравнению. Это уравнение имеет вид:
qt+1 = (qR V S)t.
Построим по приведенному уравнению триггер вначале на элементах ИЛИ-НЕ, а затем на элементах И-НЕ. Для этого опустим верхние индексы и преобразуем хто уравнение так, чтобы оно не содержало операции конъюнкции:
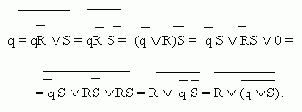
Полученное выражение определяет схему с обратной связью, которая приведена на рис. 9,а. Пользуясь равенством
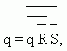
получаем схему триггера типа R-S на элементах И-НЕ, изображенную на рис. 9,б. Кружки на входах условного обозначения триггера показывают, что изменение состояния триггера должно происходить при действии сигнала, соответствующего
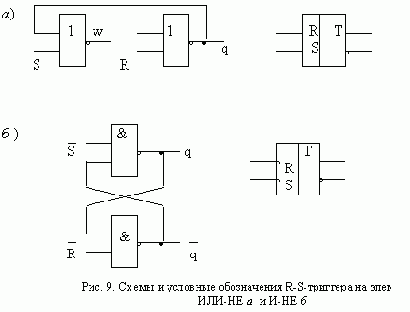
нулю.
Для того чтобы лучше представить работу триггера, проанализируем схему на рис. 9,а. Обозначим выход первой логической схемы буквой w и вычислим выходные сигналы логических элементов для различных значений входных сигналов.

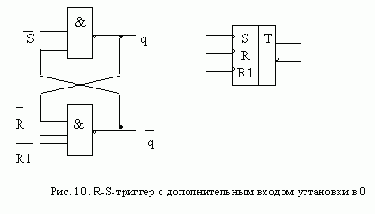
Действуя описанным способом, нетрудно построить и проверить работу R-S-триггеров с дополнительными входами установки в нуль и единицу. Например, работа триггера с дополнительным входом R1 описывается характеристическим уравнением:
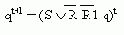
Схема триггера, построенная по этому уравнению на элементах И-НЕ, приведена рис. 10.
Пред.Страница
След.Страница Раздел Содержание
Асинхронным
. Следует заметить, что в дальнейшем при более детальном анализе процесса работы автомата придется отказаться от этого определения и допустить наличие неустойчивых состояний.Пред.Страница
След.Страница Раздел Содержание
Дискретного времени
. Входные сигналы такого автомата подобны сигналам импульсного типа (рис. 1,а). При этом были приняты следующие ограничения: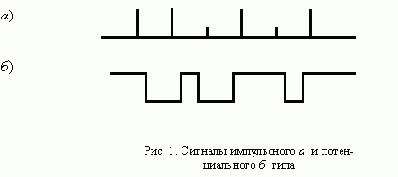
- сигналы могут поступать на вход автомата только в строго определенные моменты времени, задаваемые тактирующей последовательностью СИ с постоянным периодом Т;
- длительность входных сигналов t пренебрежимо мала (t ® 0);
- в промежутках между тактирующими сигналами на входе автомата сигнал отсутствует.
Модель автомата, построенная для токого сигнала, соответствует схемам, работающим с сигналами импульсного типа, элементы которых не имеют гальванической связи.
Входные сигналы асинхронного автомата подобны сигналам потенциального типа (рис. 1,б ). Такие сигналы должны обладать следующими свойствами:
- сигнал присктствует на входе автомата в каждый момент времени;
- длительность входного сигнала не ограничена и превышает некоторую минимальную величину t0;
- изменения входного сигнала могут происодить в произвоьные моменты времени.
Перечисленные свойства позволяют считать, что асинхронный автомат работает в непрерывном времени.
Ограничимся, так же как и для синхронного автомата, рассмотрением только двоичных входных сигналов. При этом модель асинхронного автомата может быть использована для описания работы схем, построенных из элементов потенциального типа. Допустим, что под действием входного сигнала pk синхронный автомат А переходит в состояние si. Согласно приведенным свойствам сигналов потенциального типа, pk присутствует на входе автомата и после того, как свершится переход, причем момент его окончания заранее не известен. Следовательно, выполнив такой переход, автомат должен оставаться в состоянии si до следующего изменения сигнала на входе. Описанную ситуацию можно обобщить в виде следующего определения. Если автомат совершает переход из некоторого состояния sj под действием сигнала pk в состояние si, т. е. j(sj, pk) = si, и остается под действием сигнала pk в этом же состоянии j(sj, pk) = si, то такое состояние называетсяустойчивым.
Приведенное определение позволяет нам уточнить понятие асинхронного автомата. Автомат, все состояния которого устойчивы, называется
Функциями возбуждения
. В качестве элементов памяти на практике чаще всего используют элементарные автоматы.В приведенной схеме наборы значений входных переменных x1, x2, ..., xn соответствуют буквам входного алфавита Р абстрактного автомата, наборы выходных переменных z1, z2, ..., zm - буквам выходного алфавита W, y1, y2, ..., yh
- состояниям абстрактного автомата. Пред.Страница След.Страница Раздел Содержание
Функциямиями выходов
автомата.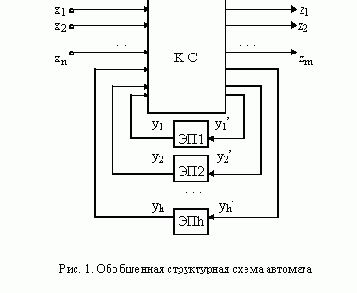
Рассматриваемая схема состоит из двух частей: комбинационной схемы (КС) и набора элементов памяти (ЭП). Переменные y1, y2, ..., yh, соответствующие выходным сигналам элементов памяти, называют внутренними переменными автомата. Переменные y1', y2', ... , yh' используются в схеме для обозначения входных сигналов, изменяющих состояние элементов памяти, и называют
Гонками
элементов памяти. При этом говорят, что состязание выигрывает элемент, обладаюший наименьшей задержкой.Состязания элементов памяти приводят к тому, что автомат при зменении состояния не сразу оказывается в том состоянии, которое запланировано условиями работы, а переходит в него через несколько нпредусмотренных транзитных состояний. В результате такого перехода, независимо от соотношений задержек элементов памяти, авомат достигает того состояния, в которое он должен перейти, то состязания называются
некритическими. Если же существует жотя бы одно сочетание значений задержек элементов памяти, при котором автомат не достигает запланированного состояния, то состязания называются критическими.
Рассмотрим, как происходят состязания на примерах, используя таблицу переходов, приведенную на рис. 3. В клетках таблицы, соответствующих сходным состояниям, находятся кружки с цыфрой. Каждая цыфра является номером рассматриваемого примера. Точками в таблице отмечены клетки, соответствующие транзитным состояниям, а кружочками с точкой - состояния, в которых оказывается автомат после завершения перехода. Горизонтальные линии со стрелкой определяют изменения входных сигналов, вертикальные сплошные линии - переходы автомата, а пунктирные линии - переходы обусловленные состязаниями.
Первый пример показывает как совершаются переходы в приведенной таблице. При этом автомат проходит последовательность состояний 000-001-101-111. Заметим, что в этой последовательности каждый переход в новое состояние совершается с изменением значения только одной внутренней переменой (одного элемента памяти), поэтому состязания отсутствуют.
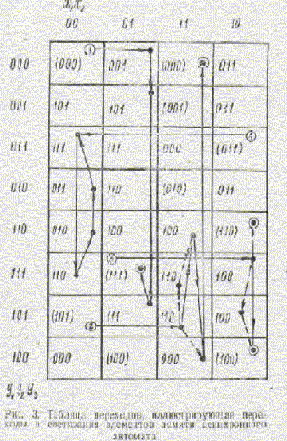
Во втором примере первый переход в последовательности состояний 101-110 выполняется с изменением значений двух внутренних переменных y2
и y3. Если время задерхки элементов памяти, соответствующим этим переменным, одинаково t32 = t33, то состязания отсутствуют и автомат проходит последовательность состояний 101 - 110-100-000.
Если же t32 < t33, то состязание выигрывает второй элемент памяти и из состояния 101 автомат попадает в состояние 111, совершая незапланированный переход. В этом случае автомат проходит последовательность состояний 101-111-110-100-000, заканчивающуюся устойчивым состоянием 000, в которое автомат должен попасть при отсутствии состязаний. Если t32
> t33, то автомат проходит последовательность состояний 101-100-000 и так же достигает заданного устойчивого состояния 000. Следовательно, в рассматриваемом случае имеют место некритические состязания. Пример показывает также, что некритические состяния огут изменять время, затрачиваемое автоматом на смену состояния, поскольку автомат может совершать различное число переходов в зависимости от соотношения между задежками.
В третьем примере (при отсутствии состязаний) автомат должен из состояния 111 перейти в состояние 100. Если же t32 > t33, то состязани выигрывает третий элемент памяти, и автомат вместо состония 100 оказывается в состоянии 110, которое является устойчивым. В этом случае имеют место критические состязания, поскольку автомат не достигает заплпнированного состояния 100.
Четвертый пример, приведенный в таблице, не связан с состязаниями элементов памяти. Он представляет собой иллюстрацию явления, встречающегося в асинхронных автоматах, которое называется генерацией. Это явление заключается в том, что автомат последовательно совершает переходы между транзитными состояниями, возвращаясь каждый раз в исходное состояние. Генерация прерывается при изменении входных сигналов. Однако при этом сосояние, в котором окажется автомат, зависит от того, с каким транзитным состоянием совпало изменение входного сигнала.
В заключение отметим, что одной из основных задач стадии структурного синтеза асинхронных автоматов является построение схемы без критических состязаний. Эта задача решается обычно на этапе кодирования состояний автомата.
Пред.Страница
След.Страница Раздел Содержание
ЭВРИСТИЧЕСКИЙ СПОСОБ КОДИРОВАНИЯ
Универсальный способ кодирования редко используется на практике для реализации автоматов с большим числом состояний, поскольку схемы в этом случае получаются весьма сложными за счет большого чсисла элементов памяти. Чаще всего при решении практических задач применяют эвристический способ, основанный на последовательном введении дополнительных состояний и увеличении числа внутренних переменных. В качестве иллюстрации этого способа рассмотрим два примера.
Прежде всего попытаемся реализовать автомат А1 с использованием двух внутренних переменных. Для этого воспользуемся графом связи этого автомата, изображенным на рис. 4,б. Нетрудно убедиться в том, что закодировать такой граф и помощью четырех кодов таким образом, чтобы при каждом переходе изменялось значение только одной переменной, невозможно. Выберем вариант кодирования, при котором наибольшее число переходов выполняется с изменением одной переменной (в нашем примере два перехода), и введем дополнительное состояние для перехода, при котором изменяются две переменные. В результате получаем граф, приведенный на рис. 5. Таблица переходов автомата при таком кодировании изображена в виде табл. 4.
,
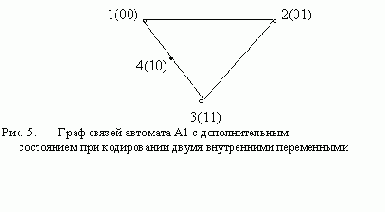
В качестве второго примера рассмотрим кодирование автомата А2, заданного табл. 5. Граф связей этого автомата приведен на рис. 6. Для однозначного кодирования четырех состояний достаточно двух внутренних переменных. Однако выполнить кодирование без состояний с помощью двух переменных оказывается невозможно. Увеличим число внутренних переменных до трех и снова попытаемся произвести кодирование без введения дополнительных состояний.
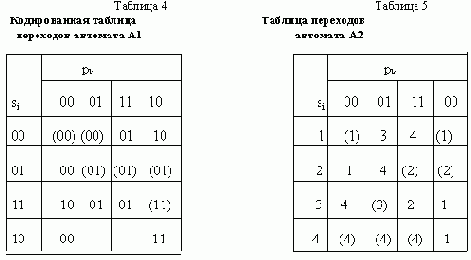
Рассматривая различные варианты, нетрудно убедиться, что получить кодирование без состояний в этом случае также невозможно. Выберем вариант кодирования, позволяющий получить наибольшее число переходов с изменением одной переменной и введем дополнительные состояния. В результате получаем граф автомата, изображенный на рис. 6,б. Используя этот граф, нетрудно построить кодированную таблицу переходов автомата А2 (табл. 6).
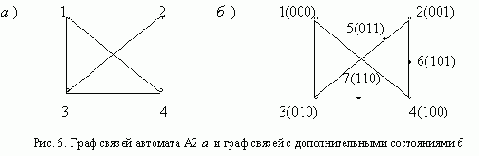
В заключение отметим, что описанный универсальный способ кодирвания не является единственным. Например, в работах [1, 3] можно найти описание способа Хаффмэна, который позволяет закодирвать любой автомат, имеющий m состояний, используя 2]log2m[ - 1 элементов памяти, где ]a[ означает ближайшее целое не меньше а. На практике же для построения схем без состояний чаще всего применяют структурный способ, основанный на использовании удвоенного числа элементов памяти. Этот способ будет рассмотрен подробнее в параграфе, посвященном построению элементов памяти, а также в следующем выпуске.
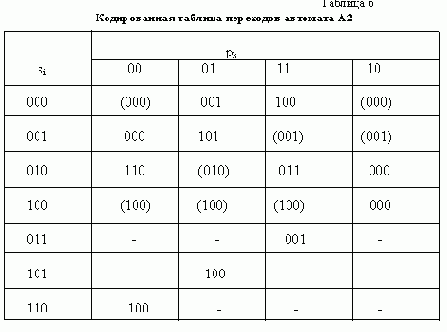
Пред.Страница
След.Страница Раздел Содержание
Кодирование с числом элементов памяти, равным числу состояний
Этот способ кодирования заключается в том, что каждому из l состояний автомата ставится в соответствие один элемент памяти. В каждый момент времени только один элемент памяти должен находиться в состоянии “1”, а остальные - в состоянии “0”, поскольку автомат может находиться только в одном состоянии. Пример кодирования пяти состояний описанным способом приведен в табл. 11. Используемый способ часто называют кодированием с применением кодов “один из l”. Следует отметить, что этот способ кодирования позволяет упростить процедуру построения функций возбуждения и функций выходов за счет исключения этапа минимизации. Остановимся на этом вопросе подробнее.
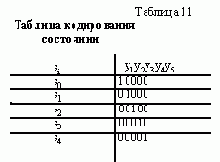
Если для кодирования состояний используются l двоичных переменных у1, y2
, ..., yl, то существует 2l
различных двоичных наборов значений этих переменных. Обозначим множество всех двоичных наборов Н. Разобьем это множество на l пересекающихся подмножеств H1, H2, ..., Hl
таким образом, чтобы в каждое подмножество Hl входили 2l-1 двоичных наборов, определяющих переключательную функцию вида yi. В каждое подмножество Hi
входит только один набор ~xi, используемый при кодировании. Он состоит из l - 1 нуля и одной единицы, стоящей на i-м месте. При этом множество Hi ' = Hi - ~xi, представляет собой совокупность неиспользованных двоичных наборов.
Пусть автомат переходит из состояния s', которому приписан код ~xi , в состояние s”, которому приписан код ~xi, под действием набора входных сигналов d1, d2, ...,dn. Если в качестве элемента памяти используется триггер D, то функция возбуждения, реализующая такой переход , имеет вид :
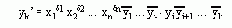
Представим эту функцию следующим образом: yk' = x1d1 x2d2
... xndnc(у1, y2, ..., yl). Функция c(у1, y2, ..., yl). является неполностью определенной переключательной функцией. Доопределим ее единицами на всех наборах, входящих в множество Hi'. В результате получаем функцию, совокупность единичных наборов которой совпадает с множеством Hi. Согласно построению, такая функция является переменной yi, поэтому имеем yk' = x1d1 x2d2
... xndn уi
Приведенные рассуждения показывают, что при выбранном способе кодирования каждый дизъюнктивный член функций возбуждения (функций выхода) содержит только одну внутреннюю переменную, определяющую соответствующее состояние автомата. Пред.Страница След.Страница Раздел Содержание
КОДИРОВАНИЕ СОСТОЯНИЙ
Состязания возникают в схемах, построенных на реальных элементах памяти с задержками, только в тех случаях, когда срабатывают одновременно несколько элементов памяти. Следовательно, для того, чтобы построить схему без состязаний, необходимо закодировать состояния автомата таким образом, чтобы при каждом переходе изменялось состояние только одного элемента памяти. Например, если в автомате определен переход из состояния si в состояние sj, то их следует кодировать соседними кодами. Напомним, что соседними называются коды, отличающиеся значением только одного разряда.
Если автомат имеет l состояний, то кодирование соседними наборами при использовании h = ]log2l[ внутренних переменных в большинстве случаев выполнить невозможно, поэтому в процессе кодирования расширяют алфавит состояний автомата и вводят дополнительные неустойчивые состояния, которые обеспечивают реализацию всех переходов в схеме с изменением только одного элемента памяти.
Пред.Страница
След.Страница Раздел Содержание
Кодрование состояний с использованием соседей первого и второго рода
Метод кодирования состояний, основанный на применении соседей, не имеет строгого обоснования. С его помощью, как правило, удается получить некоторое уменьшение сложности блока комбинационной схемы, реализующего функции возбуждения. При изложении основ этого метода мы будем предполагать, что в качестве элемента памяти используется триггер Д. Однако на практике его применяют и для элементов памяти других типов.
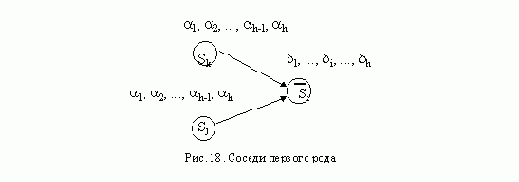
| Определение. Если два состояния sk иsj под действием одного и того же входного сигнала х переходят в одно и то же состояние s1 , то они называются соседями первого рода. |
На рис. 18 приведен фрагмент графа автомата. иллюстрирующий это определение. Закодируем соседей первого рода показано на рис. 18. Тогда элементарные соседними кодами a1, a2, ..., ah-1, ah и a1, a2, ..., ah-1, щ ah, как это конъюнкции, определяющие состояния sk и sj
, войдут во все функции возбуждения yi ', для которых соответствующий компонент di = 1. Найдем аналитическое выражение для части функций возбуждения, содержащей эти элементарные конъюнкции
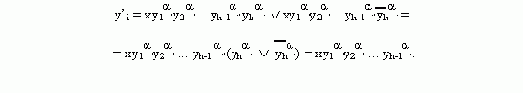
Пред.Страница След.Страница Раздел Содержание
Обобщенная структурная схема автомата
На стадии абстрактного синтеза обычно пользуются представлением автомата в виде одного блока, имеющего один вход и один выход. На стадии структурного синтеза автомат изображают в виде обобщенной структурной схемы, приведенной на рис. 1 т n входных и m выходных каналов, по которым в подавляющем большинстве случаев передаются двоичные сигналы x1, x2, ..., xn
и z1, z2, ..., zm. Переменные x1, x2, ..., xn
называют
ОБЩИЕ ПОЛОЖЕНИЯ
Особенности асинхронного автомата, или точнее асинхронной модели автомата, определяются свойствами входных сигналов. Напомним, что при построении модели автомата синхронного типа мы пользовались понятием
ОПИСАНИЕ РАБОТЫ АСИНХРОННОГО АВТОМАТА
Работа асинхронного автомата, так же как и автомата синхронного типа, может быть описана с помощью таблицы переходов и выходов или с помощью графа. Однако переход к сигналам, обладающим ненулевой длительностью, несколько усложняет такое описание.
Остановимся вначале на способе построения графа асинхронного автомата по заданному графу синхронного автомата. Пусть задан синхронный автомат, граф которого приведен на рис. 2,а. При построении этого графа длительность входных сигналов не учитывалась. Если же считать, что импульсные сигналы, подаваемые на вход, обладают конечной длительностью, то необходимо уточнить, в каком состоянии должен находиться автомат в момент действия каждого сигнала. Это можно сделать путем введения дополнительных состояний в заданный граф для каждого перехода, как это показано на рис. 2,б. Полученный граф определяет асинхронный автомат, поскольку все состояния автомата являются устойчивыми
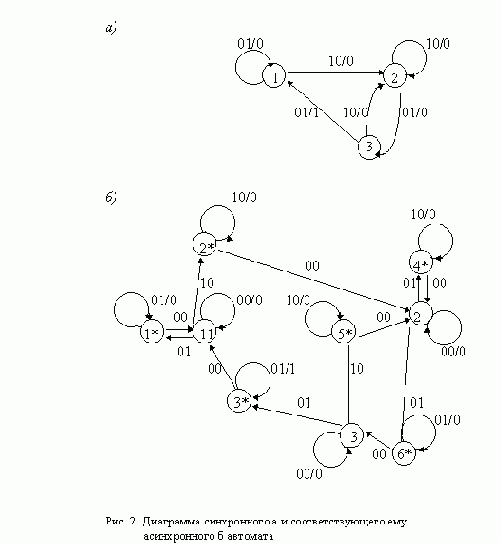
В асинхронном автомате все переходы осуществляются между устойчивыми состояниями, что создает дополнительные сложности при построении таблицы переходов. Если состояние si является устойчивым, то в клетке таблицы переходов, определяемой строкой, отмеченной состоянием si, и столбцом, отмеченным входным сигналом pk, должен быть записан символ состояния si, поскольку j(si, pk) = si. Таким образом, для устойчивых состояний в таблице переходов асинхронного автомата необходимы дополнительные средства, указывающие, в какое состояние должен перейти автомат при изменении входного сигнала. Это затруднение решается следующим образом. Процесс изменения состояния автомата разбивается на два этапа, полагая, что вначале происходит изменение входных сигналов, а состояние автомата остается неизменным, а затем уже происходит изменение состояния при новых значениях входных сигналов.Первому этапу этого процесса соответствует перемещение по строке таблицы переходов, отмеченной старым состоянием, в столбец отмеченный новыми значениями входных сигналов. Итак, первый этап однозначным образом определяет новую клетку таблицы, которая соответствует переходному состоянию автомата.
Такие состояния будем называть транзитивными. Запишем в этой клетке символ того состояния, в которое должен перейти автомат. При этом второму этапу изменения состояния соответствует перемещение по столбцу, определяемому новыми входными сигралами, в строку, отмеченную тем состоянием, в которое автомат должен перейти. Для того чтобы не путать устойчивые состояния с указателями перехода, используемыми на втором этапе, условимся заключать символы, соответствующие устойчивым состояниям, в круглые скобки. Примером таблицы переходов и выходов асинхронного автомата является табл. 1. Эта таблица построена по графу, приведенному на рис. 2,б.

Рассмотрим, как выполняются переходы в табл. 1 на примере. Допустим, что автомат находится в состоянии 3 под действием входных сигналов 00. Согласно таблице переходов, это состояние является устойчивым. Если теперь значение входных сигналов изменится на 10, то для того, чтобы найти в какое состояние перейдет автомат, необходимо выполнять перемещение по третьей строке в столбец, отмеченный сигналами 10. В определенной таким образом клетке таблицы находится номер состояния, в которое переходит автомат - это состояние 5*. Перемещаясь по вертикали в столбце 10 до строки 5*, находим, что это состояние является устойчивым. Следовательно, переход завершен. В рассмотренном примере при переходе из одного устойчивого состояния в другое автомат миновал одно транзитное состояние. В общем случае изменение состояния автомата может происходить с переходом через несколько транзитных состояний, которые, конечно, должны быть расположены в одном и том же столбце таблицы переходов. Примеры таких переходов будут приведены в следующем параграфе.
Пред.Страница
След.Страница Раздел Содержание
Основные этапы структурного синтеза
Процедуру структурного синтеза удобно рассматривать расчленив ее предварительно на несколько связанных между собой этапов.
1. Выбор структурной схемы автомата. Этот этап синтеза во многом определяет последовательность построения схемы. Примеры того, как заданная система элементов влияет на структурную схему автомата, были приведены в предыдущем параграфе. Структурные схемы автомата, применяемые при построении схемы на потенциальных элементах, будут рассмотрены в п. 9, а структурные схемы, использующие типовые блоки, будут описаны в п. 10. Основная трудность этого этапа заключается в отсутствии формальных критериев для выбора структурной схемы. Одним из главных факторов, определяющих выбор структурной схемы, является опыт разработчика.
2. Кодирование входных и выходных сигналов . Кодирование входных сигналов заключается в том, что каждой букве pi входного алфавита абстрактного автомата однозначным образом ставится в соответствие набор значений двоичных переменных х1, х2, ..., хn. Очевидно, что кодирование является однозначным, если число букв входного алфавита не превышает числа различных двоичных наборов переменных х1, х2, ..., хn. Исходя из этого, количество двоичных переменных n, необходимое для кодирования r букв входного алфавита, можно определить из условия r Ј 2n. Кодирование выходных сигналов состоит в том, что буквам выходного алфавита wi абстрактного автомата аналогичным образом ставятся в соответствие наборы значений выходных переменных z1, z2, ..., zm. Результаты кодирования обычно заносятся в таблицы кодирования входных и выходных сигналов.
В некоторых задачах кодирования входных и выходных сигналов задается в качестве условий работы схемы на этапе абстрактного синтеза. В таких случаях в структурную схему автомата могут быть включены преобразователи кодов. При этом кодирование заключается в том, что каждому набору значений переменных х1, х2, ..., хn однозначным образом ставится в соответствие набор переменных х1', х2', ..., хq', а каждому набору переменных z1, z2, ..., zm - набор переменных z1', z2', ..., zs'. Заметим, что в качестве преобразователей кодов на практике часто используют дешифраторы. Необходимо иметь в виду, что кодирование входных и выходных сигналов может существенно влиять на сложность комбинационной части схемы так же, как и кодирование состояний автомата.
Пред.Страница След.Страница Раздел Содержание
Построение функции выхода
Пред.Страница След.Страница Раздел Содержание5. Построение функции выхода . В автомате Мили каждая функция выхода zi
определяет соответствующий компонент набора выходных сигналов. Функции выхода при структурном синтезе соответствуют функции выхода абстрактного автомата. Они зависят от внутренних переменных y1, y2, ..., yh и входных переменных х1, х2, ..., хn
. Существенно, что значения переменных, определяющих zi, относятся всегда к одному и тому же моменту времени, поэтому функции выхода являются переключательными функциями:
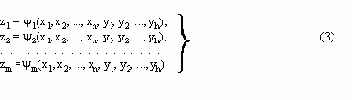
Функции выхода автомата Мура в каждый момент времени определяют совокупность выходных сигналов:
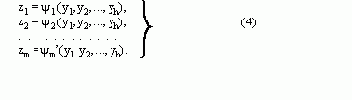
6. Реализация функций выхода и функций возбуждения. Этот этап включает в себя действия, связанные с построением аналитического представления для переключательных функций, входящих в системы (2) и (3), их минимизацию, факторизацию и преобразования в операторную форму для заданной системы элементов. Заметим, что на этом этапе целесообразно также выполнять построение преобразователей кодов, которые обычно реализуются либо как система переключательных функций, либо в виде схемы “дешифратор - шифратор”.
7. Графическое изображение полной схемы автомата. Пред.Страница След.Страница Раздел Содержание
Построение функций возбуждения
Вначале остановимся на построении функций возбуждения и выходов для автомата, заданного в виде графа. Согласно последовательности структурного синтеза, описанного в п. 2, этапу построения функции возбуждения должен предшествовать этап кодирования состояний, поэтому полагаем, что каждому узлу автомата приписан код состояния. Фрагмент такого графа приведен на рис. 11.
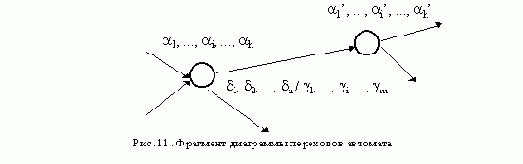
Автомат, задаваемый этим фрагментом, переходит из состояния
ПОСТРОЕНИЕ ЭЛЕМЕНТОВ ПАМЯТИ
Настоящий параграф посвящен построению элементов памяти - триггеров на элементах потенциального типа. Такие триггеры выпускаются промышленностью в виде интегральных микросхем и широко применяются для постоения узлов и блоков ЦВМ. На практике используется большое число триггеров различного вида. В основном они отличаются логикой работы, наличием синхронизации и задержки при установлении входных сигналов.
Логика работы триггера определяется его реакцией на входные сигналы. При этом различают следующие типы триггеров.
Построить схему для автомата, описанного
Построить схему для автомата, описанного в примере 1, используя в качестве элемента памяти триггер R-S.
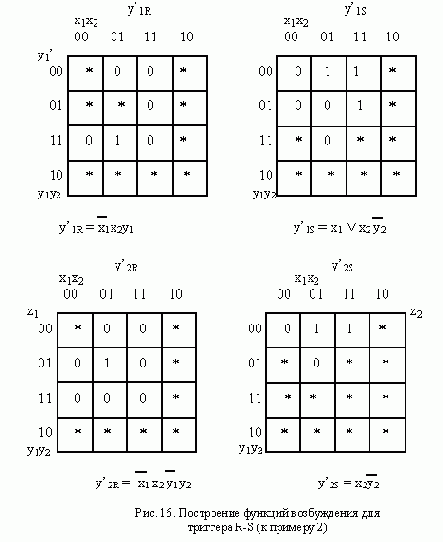
Если оставить кодирование входных сигналов и состояний таким же как и в предыдущем примере, то функции выхода в новой схеме не изменятся. Диаграммы для функций возбуждения триггера R-S изображены на рис. 16. На этом же рисунке приведены дизъюнктивные нормальные формы функций: y'1R, y'1S, y'2R, y'2S. Полная схема автомата изображена на рис. 17.
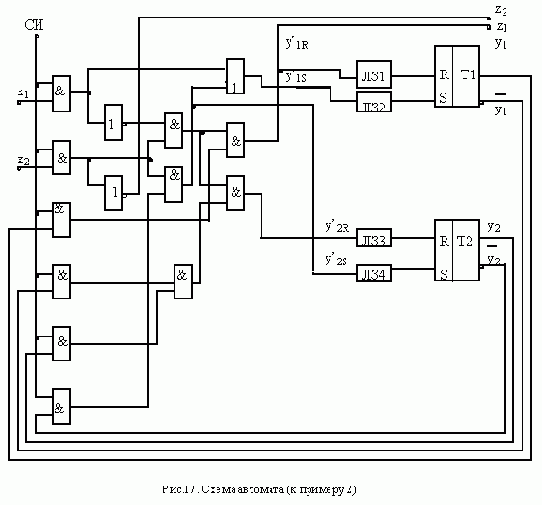
Пред.Страница
След.Страница Раздел Содержание
СОСТЯЗАНИЕ ЭЛЕМЕНТОВ ПАМЯТИ
Переход к асинхронной модели автомата связан, прежде всего, с изменнием ограничений, накладываемых на характер входных сигналов. Использование сигналов, присутствующих на входе в каждый момент времени, позволяет учитывать реальные процессы, происходящие при изменении состояний автомата, и связанные с задержками срабатывания элементов памяти. Такие задержки обусловлены как физическими прицессами, протекающими в реальных элементах, так и распределенными параметрами соединений. Величина задержки срабатывания каждого конкретного элемента памяти, как правило, неизвестна. Эта величина обычно характеризуется максимальной задержкой tзm, которая принимается пстоянной для элментов опредленного типа. При этом предполагают, что величина задержки каждого конкретного элемента tзm заключена в прделах 0 < tзi <= tзm.
Наличие различных задержек элементов памяти приводит к тому, что при переходе автомата из одного состояния в другое возникают ситуации, когда жлементы памяти срабатывают не одновременно. Последовательность срабатывания элементов памяти определяется соотношением их задержек. Очевидно, что первым должен срабатывать элемент, обладающийнаименьшей задержкой. Такое явлее называется состязаниями, или
Структурная схема на элементах импульсного типа
При построении схемы из логических элементов импульсного типа, работающих с импульсными сигналами длительностью t, и элементов памяти с выходными сигналами потенциального типа в структурную схему необходимо включить цепи синхронизации и линии задержки (ЛЗ), как это показано на рис. 4. Линии задержки в такой схеме

осуществляют задержку входных сигналов элементов памяти. Если время задержки (tз) этих линий немного больше величины t, то состояние элементов памяти остается неизменным на время действия синхронизирующего сигнала (СИ). Пред.Страница След.Страница Раздел Содержание
Структурная схема с преобразователями входных и выходных сигналов
В общем случае комбинационная схема в приведенной структурной схеме автомата может решать несколько различных задач. Если эту схему разбить на подсхемы так, чтобы каждая задача решалась отдельной подсхемой, то структурная схема автомата может быть представлена в виде, изображенном на рис. 2. В этой схеме комбинационная схема КС1 вырабатывает функции выхода, КС2 - функции возбуждения, преобразователь кодов ПК1 используется для перекодирования входных сигналов, а преобразователь кодов ПК2 - для преобразования выходных сигналов. Наличие преобразователей кодов ПК1 и ПК2 не является обязательным в структурной схеме автомата, но в некоторых случаях их включение в схему позволяет добиться уменьшения сложности, упростить процесс построения или контроля работы схемы автомата.
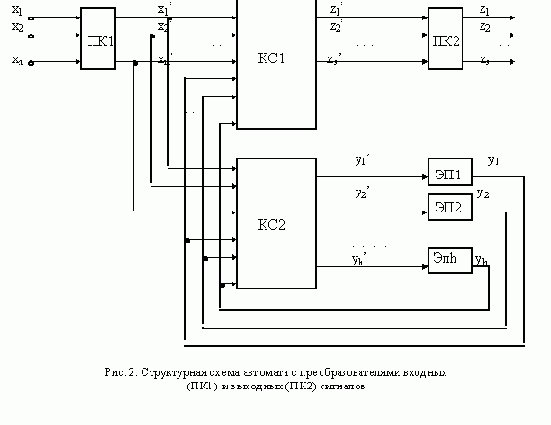
Необходимо отметить, что вид структурной схемы автомата в сильной степени зависит от используемой системы логических элементов. Например, при построении схемы на элементах с синхронизацией, сохраняющих результат логической операции до момента прихода считывающего сигнала, необходимость в элементах памяти часто отпадает. В этом случае структурная схема автомата может быть изображена в виде, приведенном на рис. 3.
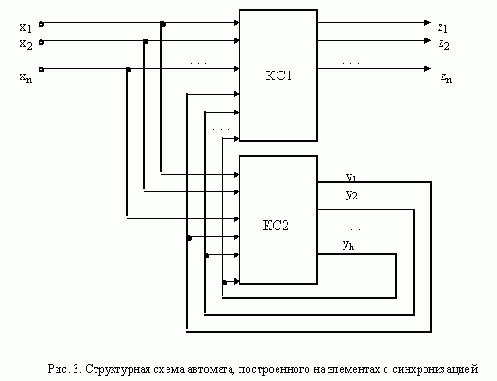
Пред.Страница
След.Страница Раздел Содержание
Структурная схема с удвоенным числом элементов памяти
В структурной схеме автомата, выполненного на элементах импульсного типа (рис. 4), линии задержки используются для сохранения схемы, относящегося к моменту прихода входного сигнала, на время действия синхронизирующего сигнала. Такая задержка изменения состояния гарантирует отсутствие состязаний в схеме , которые могли бы возникнуть во время действия синхронизирующего сигнала.
Применение линий задержки в схемах в настоящее время ограничивается трудностями их изготовления в виде микроэлектронных интегральных схем. Последнее обстоятельство привело к тому, что на практике начали заменять линии задержки элементами памяти, которые в потенциальных системах элементов, обычно строятся на основе логических элементов и не нарушают технологической целостности схемы.
Структурная схема автомата с двумя ярусами элементов памяти изображена на рис. 24. Первый ярус элементов памяти используется в схеме для хранения кода состояния, относящегося к моменту прихода входного сигнала. Выходные сигналы элементов памяти этого яруса подаются на вход комбинационной схемы. Второй ярус элементов памяти предназначен для хранения кода состояния, в которое переходит автомат в рассматриваемом такте. Этот код должен передаваться в элементы памяти первого яруса либо в момент изменения входного сигнала, либо в момент его отсутствия.
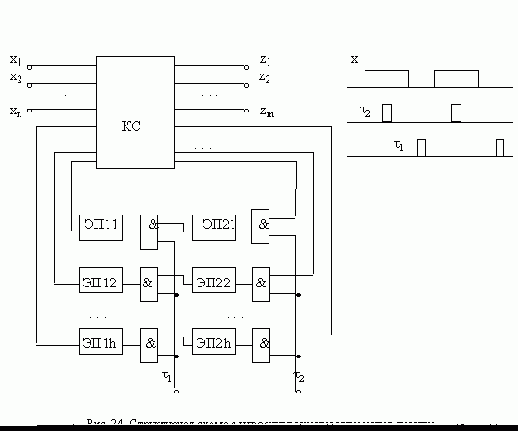
В схеме используется два синхронизирующих сигнала t1 и t2. Сигнал t2
должен быть несколько сдвинут во времени относительно момента подачи входного сигнала. Такой сдвиг позволяет исключить влияние на элементы памяти переходных процессов, обусловленных риском в комбинационной части схемы. Сигнал t2 подается на элементы конъюнкции и разрешает прохождение сигналов, соответствующих значениям функций возбуждения, на входы элементов памяти второго яруса. Сигнал t1 осуществляет передачу кода состояния из элементов памяти второго яруса в элементы памяти первого яруса. Этот сигнал должен подаваться в схеме обязательно после окончания действия сигнала t2 и входного сигнала.
Необходимо отметить, что приведенная структурная схема широко используется на практике при построении как типовых блоков цифровых вычислительных устройств: счетчиков, регистров, делителей и т. п., так и управляющих схем.
Пред.Страница
След.Страница Раздел Содержание
Структурные схемы с дешифратором
На рис. 22 приведена структурная схема автомата с двумя дешифраторами. Дешифратор ДС1 служит в схеме для преобразования входных сигналов, а дешифратор ДС2 - для преобразования кодов состояний.
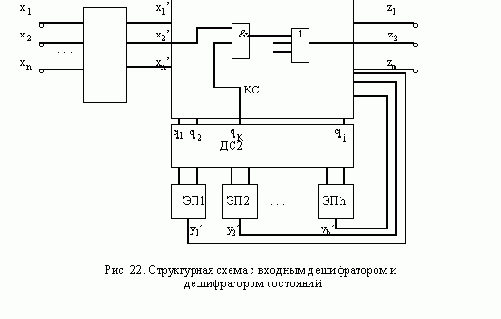
Число выходов каждого дешифратора определяется числом различных наборов значений его входных переменных. Каждых входной набор возбуждает единственный сигнал, соответствующий единице, на выходе дешифратора. Таким образом, в каждый момент времени на одном из выходов дешифратора имеется сигнал, соответствующий единице, а на остальных выходах - сигналы, соответствующие нулю. Это обстоятельство позволяет нам считать схемы с дешифратором состояний разновидностью схем с кодированием “один из l” и использовать свойства таких кодов и способы построения функций возбуждения и выходов, описанные в предыдущем параграфе, для рассмотрения схем.
Включение дешифратора входных сигналов в схему позволяет применить для описания переходов двухместные конъюнкции. При этом функции возбуждения и функции выходов могут быть представлены в виде: yi' = Ъ gkxs';
zj = Ъ gpxq'.
Принцип реализации таких функций показан на рис. 22 в поле комбинационной схемы. Пред.Страница След.Страница Раздел Содержание
СВЯЗЬ АСИНХРОННОГО АВТОМАТА С ВНЕШНЕЙ СРЕДОЙ
Использование сигналов потенциального типа, длительность которых не ограничена и время изменения не фиксировано, осложняет работу с кодами, поступающими последовательно на вход асинхронного автомата. Основная трудность заключается в том, что с помощью одного потенциального сигнала с неопределенной длительностью нельзя закодировать последовательность из одинаковых цифр. Например, пусть требуется передать на вход автомата последовательный код, состоящий и четырех единиц. Если используется двоичный потенциальный сигнал, то каждой единице будет соответствовать одно и то же значение напряжения на входе, и автомат воспримет такую последовательность как один сигнал равный единице. В общем случае такая неоднозначность при передаче последовательных двоичных кодов будет возникать для любой группы стоящих рядом одинаковых цифр.
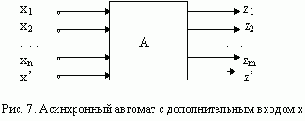
Для того чтобы сделать возможной передачу последовательных кодов при потенциальном характере сигналов, расширяют входной алфавит автомата. Такое расширение соответствует введению одной дополнительной линии передачи x’ (рис. 7), которая используется для сихронизации или для пересылки указателя при передаче последовательности одинаковых цифр. В зависимости от того, как используется линия x’, возможны несколько способов организации передачи. Рассмотрим три основных способа, которые приведены на рис. 8.
Первый способ предполагает использование линии x’ для передачи импульса определенной длительности t, который формируется для каждой позиции кода, где расположена цифра, совпадающая с предыдущей (рис. 8,а ). Этот способ соответствует преобразованию входных слов автомата, при котором между каждыми двумя одинаковыми цифрами вводится дополнительный символ-разделитель. На рис. 8,а используется даже два разделителя: один применяется в последовательности единиц, а другой - в последовательности нулей. Если обозначить r1 - разделитель единиц, а r0 - разделитель нулей, то входная последовательность 0110010 может быть записана следующим образом 01r110r0010.
В рассматриваемом случае входной алфавит должен состоять из четырех букв P = {00, 01, 10, 11}, где буквы 00 и 10 соответствуют нулю, а буквы 01 и 11 - разделителю нулей и разделителю единиц. При этом входная последовательность имеет вид: 00 10 11 10 00 01 00 10 00. Следует отметить, что использование разделителей приводит к необходимости выравнивания длины входных слов, а также к увеличению времени передачи каждого слова.
При втором способе по линии x’ передается синхронизирующая последовательность импульсов с длительностью t и периодом 2t (рис. 8,б ). Такой способ предплагает использование для каждого символа, подаваемого на основной вход автомата, двух различных кодов. Например, в случае двоичных кодов, единице ставятся в соответствие коды 10 и 11, а нулю - коды 00 и 01. При этом кодирование соседних букв в каждом входном слове должно выполняться таким образом, чтобы коды таких букв имели различные значения в позиции, соответствующей синхронизирующему сигналу. Например, последовательность 0110010, для рассматриваемого случая можно представить так: 00 11 10 01 00 11 00.
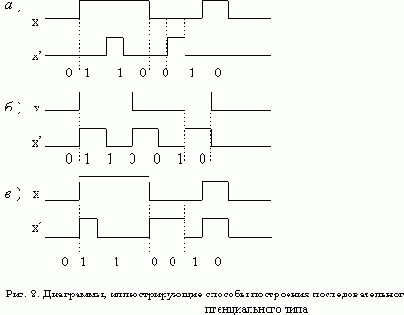
Существенно, что описанный способ построения последовательного кода не приводит к изменению длины входной последовательности и увеличению времени ее передачи.
Третий способ, изображенный на рис. 8,в отличается от предыдущего только тем, что в дополнительной линии x’ вместо импульсного сигнала используется сигнал потенциального типа. При этом кодирование выполняется таким же образом, как и в предыдущем случае.
В заключении следует отметить, что при работе с сигналами потенциального типа на стадии абстрактного синтеза автомата приходится вводить доплнительный этап, связанный с перекодированием слов заданного оператора в соответствии с выбранным способом построения последовательного кода. Если автомат должен вырабатывать также последовательный код, то необходимо предусмотреть и соответствующее кодирование выходных слов заданного оператора.
Пред.Страница
След.Страница Раздел Содержание
T - ТРИГГЕР С ЗАДЕРЖКОЙ
В качестве примера рассмотрим построение асинхронного Т-триггера с задержкой по М-S-схеме. Диаграмма переходов такого триггера изображена на рис. 15,а. Состояния на диаграмме закодированы таким образом, чтобы при каждом переходе изменялась только одна переменная. Таблица переходов, соответствующая этой диаграмме, приведена на рис. 15,б. Функции возбуждения триггеров типа R-S, построенные по этой таблице, приведены на рис. 15,в, а схема Т-триггера - на рис. 16.
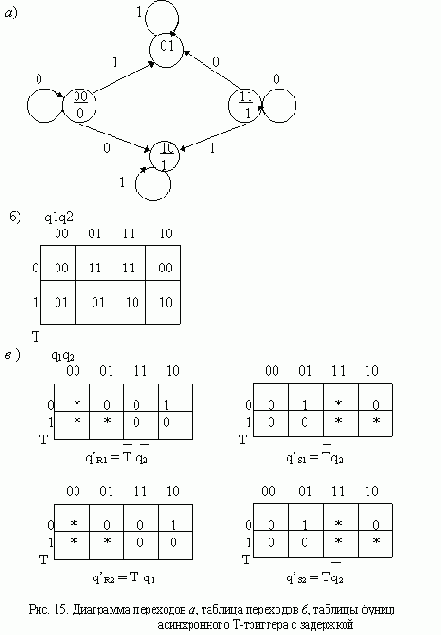
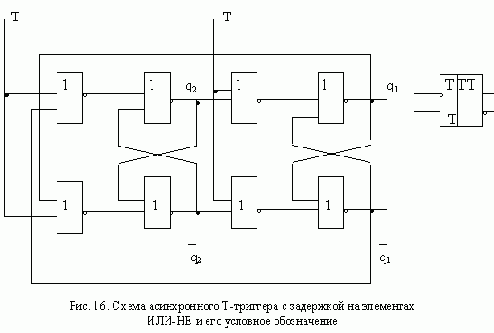
Пред.Страница
След.Страница Раздел Содержание
Типы элементов памяти
В качестве элементов памяти на стадии структурного синтеза чаще всего используют элементарные автоматы с двумя выходными сигналами. Однако в последнее время в связи с разработкой больших интегральных схем представляет интерес использование в качестве элементов памяти широко применяемых в цифровых устройствах типовых схем: счетчиков и регистров.
Элементы памяти с двумя выходными сигналами обычно называются триггерами. В большинстве случаев триггер является автоматом Мура. Он может иметь один или несколько входов. Работа триггера, как и любого автомата, описывается с помощью таблицы переходов.
На практике часто возникает задача построения триггеров из элементов заданной системы. Для этой цели используют характеристическое уравнение триггера, которое определяет состояние, в которое должен перейти триггер qt+1 в зависимости от входного сигнала xt
и состояния qt, в котором находится триггер
ТРИГГЕР D-V С ЗАДЕРЖКОЙ И СИНХРОНИЗАЦИЕЙ
В качестве примера рассмотрим построение D-V-триггера с задержкой и синхронизацией. Диаграмма и таблица переходов такого триггера изображена на рис. 21. Таблицы функций возбуждения приведены на рис. 22, а схема триггера на рис. 23.
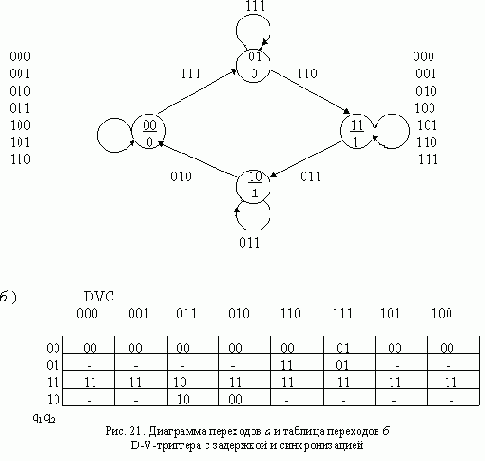
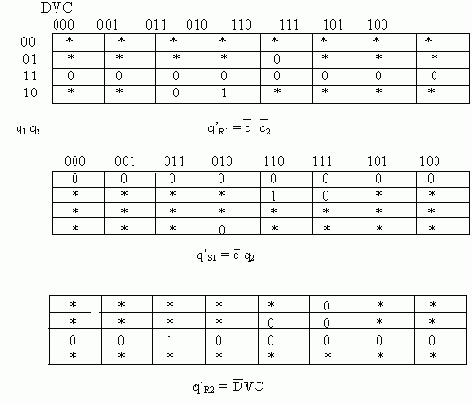
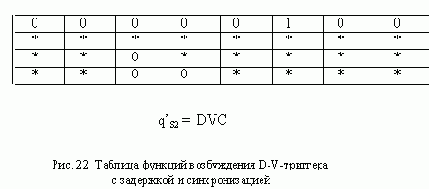
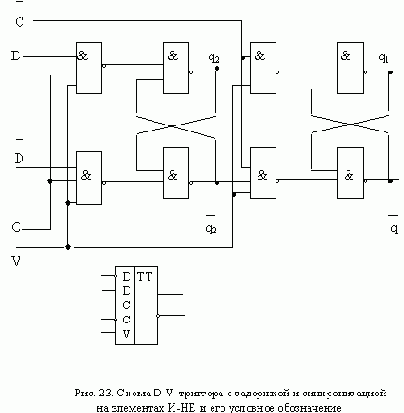
Пред.Страница
След.Страница Раздел Содержание
ТРИГГЕР J-K С ЗАДЕРЖКОЙ И СИНХРОНИЗАЦИЕЙ
Применение асинхронных триггеров с задержкой позволяет устранить состязания в схемах, но не исключает влияния задержек сигналов, подаваемых на разные входы триггера, и риска в комбинационной части схемы автомата. Чтобы устранить влияние этих факторов, используем триггер с задержкой и синхронизацией. При этом длительность синхронизирующего сигнала выбирается, как правило, меньшей, чем длительность сигналов, подаваемых на управляющие входы. Временная даграмма, приведенная на рис. 20, поясняет работу триггера с задержкой и синхронизацией. На диаграмме изображены коды, определяющие состояние входных сигналов в различные моменты времени. Анализируя эти коды, нетрудно заметить, что принятое соотношение длительности сигналов х и С равносильно ограничению допустимых последовательностей входных сигналов. Например, в рассмааемом случае за сигналом 11 должен обязательно следовать сигнал 10, но никак не сигнал 00. Эти ограничения, так же как и ограничения, возникающие вследствие задержки выходного сигнала, обычно учитывают при построении диаграмм переходов триггеров с задержкой и синхронизацией.
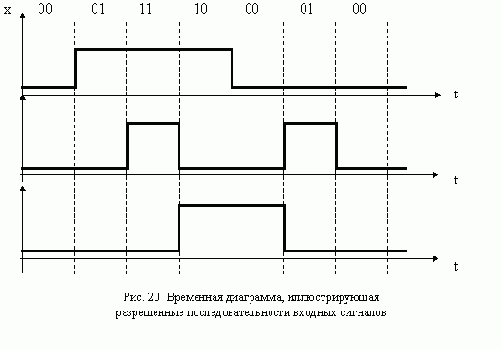
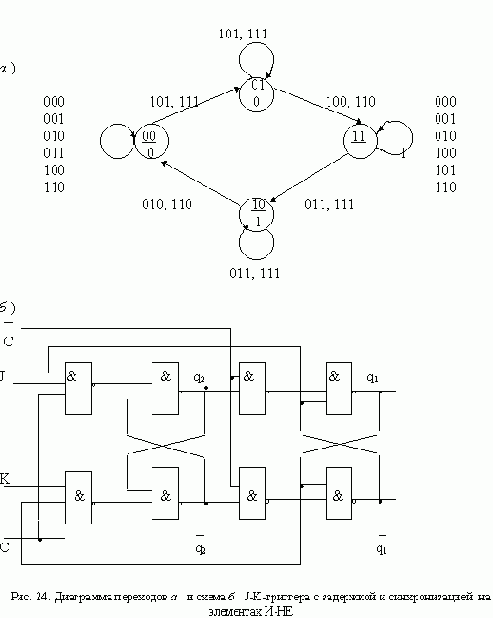
Пред.Страница
След.Страница Раздел Содержание
ТРИГГЕРЫ С СИНХРОНИЗАЦИЕЙ
В реальных схемах в результате действия паразитных задержек сигналы, подаваемые на различные входы триггера, могут приходить одновременно. Если, например, сигнал на вход R триггера типа S, находящегося в состоянии 1, придет раньше сигнала на входе S, то триггер может успеть перейти в состояние 0 на время задержки сигнала, подаваемого на вход S. Чтобы избежать таких ложных срабатываний, обусловленных задержками входных сигналов, используют синхронизирующие или, как их называют, тактирующие сигналы. При этом длительность синхронизирующих сигналов выбирается меньшей, чем длительность сигналов, подаваемых на управляющие входы. Временная диаграмма, поясняющая использование синхронизирующий сигналов, приведена на рис. 12.
Триггеры с синхронизацией должны иметь дополнительный вход С, на который подаются тактирующие сигналы. Работу такого триггера можно описать следующим образом. При отсутствии сигнала на входе С, триггер не изменяет своего состояния. Если же сигнал на входе С равен 1, то он работает как соответствующий триггер без синхронизации. Триггеры рассматриваемого типа строятся обычно на основе асинхронного R-S-триггера. Пример построения S-триггера с синхронизцией приведен на рис.13.



Пред.Страница
След.Страница Раздел Содержание
ТРИГГЕРЫ С ЗАДЕРЖКОЙ
Для того чтобы устранить состязания в схемах асинронных автоматов, используют специального вида триггеры с задержой. Выходной сигна q такого триггера изменятся в момент окончания действия входного сигнала, как показано на рис. 14. В схема, построенных на триггера с задержкой, сигналы обратной связи остаются неизменными во время действия входных сигналов, поэтому состязания в таких схемах, так же, как и схемах с двойной памятью, должны отсутствовать. Задержка выходного сигнала может быть реализована за счет увеличения числа внутренних состояний триггера. При этом необходимо ввести по крайней мере два дополнительных состояния: одно для запоминания новых входных сигналов при переходе из 0 в 1, а другое - для запоминания входных сигналов при переходе из 1 в 0. Следовательно, триггер с задержкой должен иметь не менее четырех состояний.
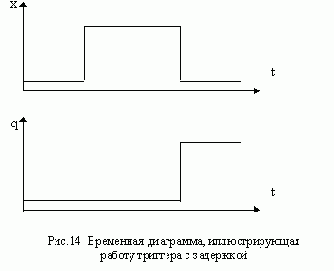
В зависимости от того, как закодировать эти состояния, можно получить различные виды триггеров. Например, если выполнить кодирование с помощью трех переменных, то можно получить триггер с задержкой на основе трех R-S-триггеров. Если же кодирование производить с использоваием двух внутренних переменных, то можно получить триггеры, построенные по M-S-схеме (сокращение от английский слов Master - Slave). При построении по M-S-схеме используют два асинхронных R-S-триггера, один из которых является главным, а второй вспомогательным.
Пред.Страница
След.Страница Раздел Содержание
УПРАЖНЕНИЯ
Пред.Страница
След.Страница Раздел Содержание
Выбор числа элементов памяти и кодирование состояний автомата
Пред.Страница След.Страница Раздел Содержание3. Выбор числа элементов памяти и кодирование состояний автомата. Кодирование состояний заключается в том, что каждому состоянию si
О S однозначным образом ставится в соответствие набор внутренних переменных у1, у2, ..., уh. Состояния и соответствующие им коды обычно представляют в виде таблицы, которая называется таблицей кодирования состояний автомата.
Если автомат имеет l состояний, то, для того, чтобы получить однозначное соответствие, необходимо иметь не менее l различных двоичных кодов. Последнее условие можно записать в виде l Ј 2h. Откуда находим
] log2l [ Ј
h, (1)
где ] a [ означает ближайшее целое, не меньшее а.
Из неравенства (1) следует, что минимальное число элементов памяти, необходимое для получения однозначного кодирования,
h = ] log2 l [.
Кодирование состояний существенно влияет на сложность комбинационной части схемы автомата. Для того, чтобы упростить комбинационную схему, часто используют избыточное кодирование, выбирая h большим, чем это необходимо для получения однозначного кодирования. Избыточное кодирование используется также для построения схем без состязаний. Кодирование состояний кажется целесообразным выполнять совместно с кодированием входных и выходных сигналов, однако такая задача оказывается весьма сложной и практически не реализуется.
4. Построение функций возбуждения.Функция возбуждения yi' определяет, какой сигнал нужно подать на вход i-го элемента памяти, чтобы получить код состояния, в которое автомат должен перейти. Функции возбуждения при структурном синтезе соответствуют функциям перехода абстрактного автомата. Это соответствие показывает, что функции возбуждения должны зависеть от внутренних переменных y1, y2, ..., yh, определяющих состояние автомата, и входных переменных х1, х2, ..., хn, относящихся к одному и тому же моменту времени. Последнее обстоятельство позволяет нам рассматривать функции возбуждения как
переключательные функции:
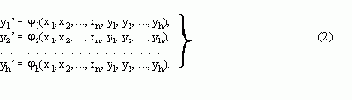
Пред.Страница След.Страница Раздел Содержание
Задача структурного синтеза
Процесс построения схемы автомата обычно разделя ют на две относительно независимых стадии: абстрактный и структурный синтез. На стадии абстрактного синтеза, исходя из заданных условий работы, выполня ется построение таблиц перех одов и выходов автомата. Задачей структурного синтеза является построение функциональной схемы автомата. Исходными данными для стадии структурного синтеза являются таблицы переходов и выходов автомата, система логических элементов, тип элемента памяти, а также дополнительные условия, накладываемые на качество и на работу схемы, например: время работы, допустимость риска, условия связи с внешней средой, стоимость и т. п.
Следует отметить, что исходные данные и круг вопросов, решаемых на стадии структурного синтеза, могут существенно изменяться. Например, в некоторых случаях при структурном синтезе решают задачу выбора т ть искомой схемы. В дальнейшем изложении совокупность исходных данных и задач а структурного синтеза предполагаются такими, как они описаны в начале насто ящего параграфа.
Пред.Страница
След.Страница Раздел Содержание
Форма Наура-Бэкуса
При описании синтаксиса конкретных языков программирования приходится вводить большое число нетерминальных символов, и символическая форма записи теряет свою наглядность. В этом случае применяют форму Наура-Бэкуса (ФНБ), которая предполагает использование в качестве нетерминальных символов комбинаций слов естественного языка, заключенных в угловые скобки, а в качестве разделителя - специального знака, состоящего из двух двоеточий и равенства. Например, если правила
®
®
<список>::= <элемент списка>.
Чтобы сократить описание схемы грамматики, в ФБН разрешается объединять правила c одинаковой левой частью в одно правило, правая часть которого должна включать правые части объединяемых правил, разделенные вертикальной чертой. Используя объединение правил, для рассматриваемого примера получаем: <список>::=<элемент списка><список>|<элемент списка>.
Пред.Страница След.Страница Раздел Содержание
" Формальные языки, грамматики и автоматы"
Основными объектами изучения научного направления "Информатика" являются модели, представимые в памяти компьютера. Методы построения подобных моделей в различных предметных областях основаны на моделях конечных автоматов и формальных грамматик. Широкое использование таких моделей в теоретических исследованиях и разработке систем, используемых на практике, позволяет рассматривать их как одну из основ образования по направлению "Информатика". Главным назначением дисциплины "Формальные языки, грамматики и автоматы" является ознакомление студентов, обучающихся по направлению "Информатика" с основами теории, методами и приемами практического использования аппарата формальных грамматик и конечных автоматов. Изучение дисциплины планируется на 5-ом семестре и включает: курс лекций ( 4 часа в неделю ), лабораторные работы ( 2 часа в неделю ) и курсовую работу.Лабораторные работы выполняются в компьютерном классе с использованием системы обучения синтаксическому анализу ( ОСА ). Эта система была разработана на кафедре Вычислительной техники в основном силами доц. Разумовского Г.В. и ассистента Кузнецова И.А. Она позволяет автоматизировать некоторые этапы синтеза магазинных автоматов и моделировать их работу.
В курсовой работе студенты реализуют программные модели магазинных преобразователей для некоторых фрагментов языков программирования.
В настоящее время ведется работа по созданию на базе курса лекций, и системы ОСА дистанционной обучающей системы, которая, в отличие от традиционных гипертекстовых представлений материала, должна обеспечивать интерактивное взаимодействие обучающегося с системой, автоматический контроль выполняемых заданий и возможность общения с преподавателем с помощью сетевых средств. Эта работа выполняется без финансовой поддержки в основном силами волонтеров - студентов. Считаю необходимым выразить благодарность моим помощницам Татьяне Карасевой и Светлане Новиковой, выполнившим преобразование текста в формат HTML.
Учитывая существующие трудности, публикацию электронной версии текста пособия предполагается выполнять частями в соответствии с планом пособия по мере их подготовки.
12.05.1998 В.Фомичев
 Содержание курса
Содержание курса4. Описание перевода и преобразователи.
5. Атрибутные грамматики и преобразователи.
6. Автоматные грамматики и конечные автоматы.
7. Абстрактный синтез автоматов.
8. Переключательные функции и синтез комбинационных схем.
9. Структурный синтез автоматов.

 2.
2. 
 4. Способы описания перевода. Бесскобочные выражения.
4. Способы описания перевода. Бесскобочные выражения.Преобразователи.
4.1. Описание перевода или трансляции .
4.1.1. Синтаксически - управляемые схемы
4.1.2. Перевод, определяемый СУ-схемой.
4.1.3. Простая СУ - схема.
4.1.4. Построение простой СУ - схемы.
4.1.5. Транслирующие грамматики
4.1.6. Входная и выходная грамматики заданной транслирующей грамматики.
4.1.7. Построение транслирующей грамматики по СУ - схеме
4.2. Бесскобочные выражения
4.2.1. Префиксная польская запись.
4.2.2. Вычисление префиксных польских записей.
4.2.3. Постфиксная польская запись.
4.2.4. Вычисление постфиксных польских записей.
4.2.5. Примеры постфиксных польских записей.
4.2.6. Примеры СУ - схем.
4.3. Магазинные Преобразователи.
4.3.1. Определение магазинного преобразователя.
4.3.2. Описание работы магазинного преобразователя.
4.3.3. Перевод определяемый преобразователем.
4.3.4. Построение преобразователя.
4.3.5. Пример построения детерминированного преобразователя.
4.3.6. Порядок построения детерминированного магазинного преобразователя.
4.4. Резюме.
4.5. Упражнения.
4.6. Термины.
Грамматика для описаний
Пусть требуется построить грамматику для описания целых и вещественных переменных. Описание переменных определенного типа должно начинаться указателем типа 'real' или 'int'.
В полном тексте описания описания переменных определенного типа могут повторяться. Например, полное описание может включать три разных описания переменных целого типа. Полное описание должно заканчиваться точкой. В качестве разделителя описаний переменных разных типов примем точку с запятой, а в качестве разделителя переменных одного типа - запятую. Структуру полного описания можно представить в виде двух вложенных списков с разделителями. Внутренний список, рассматриваемый как элемент внешнего списка, представляет собой описание переменных одного типа. Он имеет заголовок в виде указателя типа, за которым следует последовательность идентификаторов, разделенных запятыми. Внешний список использует в качестве разделителя точку с запятой. Схема грамматики рассматриваемого вида может быть записана так:
Г1. 26 : R = {
Пред.Страница След.Страница Раздел Содержание
Грамматика, задающая последовательность операторов присваивания
Допустим, что в правой части оператора присваивания могут быть использованы только выражения без скобок, описываемые грамматикой Г1. 24. В качестве разделителя операторов в последовательности примем точку с запятой. Учитывая, что последовательность операторов соответствует списку с разделителями в виде точки с запятой, и, используя определенную ранее конструкцию идентификатора, получаем искомую схему грамматики в виде:
Г1. 27 : R = { ®
,
® ,
Пред.Страница След.Страница Раздел Содержание
Грамматики для арифметических выражений
Условимся рассматривать арифметические выражения, использующие только знаки сложения и умножения. Вначале построим грамматику для выражений без скобок. Такие выражения представляют собой цепочки, которые можно рассматривать как списки с разделителями, в которых роль разделителей выполняют знаки операций. В соответствии с этой аналогией получаем схему грамматики, в которой символ обозначает идентификатор, определение которого приведено выше.
Г1. 23 : R = {
®
Чтобы построить грамматику, допускающую использование в арифметических выражениях скобок без вложенности, представим структуру таких выражений в виде списка с разделителями, элементами которого являются выражения без скобок или выражения без скобок, заключенные в скобки. Разделителями этого списка являются знаки операций. Такой структуре соответствует следующая схема грамматики:
Г1. 24 : R = {
®
,
,
®,
® $ }.
Для построения грамматики арифметических выражений, допускающих применение вложенных скобок, следует предусмотреть возможность использования в качестве элемента списка не только выражения без скобок, но и выражения, в котором могут быть использованы скобки. Схема грамматики, учитывающая эту возможность, может быть записана в виде:
Г1. 25 : R = {
®
®
® $ }.
Пред.Страница След.Страница Раздел Содержание
Грамматики, описывающие целые числа без знака и идентификаторы
Целые числа представляют собой последовательность цифр, поэтому их можно рассматривать как списки, элементами которых являются цифры. Используя в качестве аналога грамматику, задающую список без разделителей, получаем схему грамматики для целых чисел в виде:
Г1. 20:
®
Структуру идентификатора можно представить в виде двух компонентов: начала и основной части. Началом может быть любая из букв, а основная часть представляет собой список без разделителей, элементами которого могут быть либо буквы, либо цифры. Используя выделенные компоненты, получаем схему грамматики вида:
Г1. 21: R ={ ®
®
®
® $,
Если наложить ограничения на длину идентификатора, например, допустить использование идентификаторов, состоящих только из трех символов, то схема грамматики получается проще.
Г1. 22 : R = { ®
®
®
Пред.Страница След.Страница Раздел Содержание
Грамматики, описывающие условные операторы и операторы цикла
Допустим, что рассматриваются условные операторы, аналогичные используемым в языке Паскаль, с разделителями 'if', 'then', 'else'. В качестве условия в таких операторах разрешается использовать отношения, состоящие из двух идентификаторов, соединенных знаками = и <. Структура такого оператора определяется двумя видами последовательностей фиксированной длины, для описания которых можно воспользоваться простым перечислением компонентов. Первая последовательность определяет полный и сокращенный условные операторы, а вторая - конструкцию "отношение". Схема грамматики, задающая эти последовательности, может быть изображена так:
Г1. 28 : R = {
® .if.
} .
В этой грамматике
Г1. 29: R = {
Г1. 30: R = {
® .repeat.
}.
Пред.Страница След.Страница Раздел Содержание
не имеют никаких ограничений на
Грамматики типа 0, которые называют грамматиками общего вида, не имеют никаких ограничений на правила порождения. Любое правило
r = h ® y
может быть построено с использованием произвольных цепочек
h, y О
(Vт И Va)*. Например,
Пред.Страница След.Страница Раздел Содержание
не допускают использования любых правил.
Грамматики типа 1, которые называют также контекстно-зависимыми грамматиками, не допускают использования любых правил. Правила вывода в таких грамматиках должны иметь вид:
c1c2 ® c1w c2,
где c1,
c2 - цепочки, возможно пустые, из множества
(Vт И Va)*,
символ <А> О Va
и цепочка w О (Vт И
Va)*. Цепочки c1
и c2 остаются неизменными при применении правила, поэтому их называют контекстом (соответственно левым и правым), а грамматику - контекстно зависимой.
Грамматики типа 1 значительно удобнее на практике, чем грамматики типа 0, поскольку в левой части правила заменяется всегда один нетерминальный символ, который можно связать с некоторым синтаксическим понятием, в то время как в грамматике типа 0 можно заменять сразу несколько символов, в том числе и терминальных.
Например, грамматика:
Г1. 4:
Vт = {a, b, c, d}, Va = {, , }
R = { ® aA,
A ® AA,
AAA ® AA,
A ® b,
bA ® bcdA,
b ® ba }
является контекстно-зависимой, поскольку второе и шестое правила имеют непустой левый контекст, а третье и пятое правила содержат оба контекста. Вывод в такой грамматике может иметь вид:
Ю a
Ю a Ю ab Ю abb Ю abba.
Пред.Страница След.Страница Раздел Содержание
Правила вывода таких грамматик имеют
Грамматики типа 2
называют контектно-свободными и бесконтекстными грамматиками ( КС-грамматики или Б-грамматики).
Правила вывода таких грамматик имеют вид:
® a,
где О
Va и a О (Vт И Va)*.
Очевидно, что эти правила получаются из правил грамматики типа 1 при условии c1
= c2 = $. Поскольку контекстные условия отсутствуют, то правила КС-грамматик получаются проще, чем правила грамматик типа 1. Именно такие грамматики используются для описания языков программирования. Примером КС-грамматики может служить следующая:
Г1. 5:
Vт = {a, b}, Va = {},
R = { ®
aa,
® bb,
® aa,
® bb}.
Эта грамматика порождает язык, который состоит из цепочек, каждая из которых в свою очередь состоит из двух частей, цепочки
b О Vт* и зеркального отображения этой цепочки b'.
L( Г5 ) = { bb' | b ОVт+},
где Vт+ - это множество Vт*
без пустой цепочки. С помощью правил этой грамматики может быть построена, например, следующая цепочка:
Ю aa
Ю abba Ю abaaba
Ю ababbaba.
Пред.Страница След.Страница Раздел Содержание
в таких грамматиках имеют вид:
Грамматики типа 3
называют автоматными грамматиками (А - грамматиками). Правила вывода в таких грамматиках имеют вид:
® a
или ® a
или ®
a,
где a О Vт, , О Va, причем грамматика может иметь только правила вида
® a - правосторонние правила, либо только вида ® a
- левосторонние правила. Примерами автоматных грамматик могут служить правосторонняя грамматика Г1. 6
и левосторонняя грамматика Г1. 7.
Г1. 6:
Vт = {a, b}, Va = {, },
R = { ® a,
® a,
® b,
® b
Г1. 7:
Vт = {a, b}, Va = {, },
R = { ® b,
® b,
®
Эти грамматики являются эквивалентными и порождают язык
L(Г7) = {a...ab...b | n,m > 0}.
Между множествами языков различных типов существует отношение включения:
{ L типа 3 } М
{ L типа 2 }
М{ L типа 1 } М{ L типа 0}.
Доказано, что существуют языки типа 0, не являющиеся языками типа 1, языки типа 2, не являющиеся языками типа 1, и языки типа 3, не являющиея языками типа 2.
Учитывая, что наибольшее практическое применение находят грамматики типа 2 и типа 3, дальнейшее изложение посвящается рассмотрению именно этих типов грамматик.
Пред.Страница След.Страница Раздел Содержание
Итерационная форма
Для получения более компактных описаний синтаксиса применяют итерационную форму описания. Такая форма предполагает введение специальной операции, которая называется итерацией и обозначается парой фигурных скобок со звездочкой. Итерация вида {a}* определяется как множество, включающее цепочки всевозможной длины, построенные с использованием символа a, и пустую цепочку.
{a}* = {$, a, aa, aaa, aaaa,...}.
Иcпользуя итерацию для описания множества цепочек, задаваемых символическими правилами, для списка получаем:
Например, описание множества цепочек, каждая из которых должна начинаться знаком # и может состоять из произвольного числа букв x и y, может быть представлено в итерационной форме так:
® #{x | y}*
.
В итерационных формах описания наряду с итерационными cкобками часто применяют квадратные скобки для указания того, что цепочка , заключенная в них, может быть опущена. С помощью таких скобок правила:
® xyz и
® xz
могут быть записаны так:
® x[y]z.
Пред.Страница След.Страница Раздел Содержание
Левый и правый выводы
Среди всевозможных выводов наибольший интерес представляют следующие два типа выводов.
| Определение. Если при построении вывода цепочки a при каждом применении правила заменяется самый левый нетерминальный символ, то такой вывод называется левым или левосторонним выводом a. Если при построении вывода a, всегда заменяется самый правый нетерминальный символ промежуточной цепочки, то вывод называется правым или правосторонним выводом a. |
Например, приведенный выше вывод цепочки i * i + i в грамматике Г1. 9 является левосторонним выводом. Следует отметить, что различным выводам цепочки i+i в грамматике
Г1. 9 соответствует одно и то же синтаксическое дерево. Аналогичная ситуация имеет место и при выводе цепочки
i * i + i.
Пред.Страница След.Страница Раздел Содержание
Неоднозначные и эквивалентные грамматики
Существуют грамматики, в которых одна и та же цепочка может быть получена с помощью различных выводов. Например, в грамматике Г1. 10 цепочка abc
может быть получена с помощью двух различных выводов, и ей соответствуют два различных синтаксических дерева.
Г1. 10:
Vт = {a, b, c, d}, Va = {, , },
R = { ® ,
® a,
® ac,
® b,
® cb}.
Первый вывод этой цепочки имеет вид :
1) Ю
Ю b Ю acb,
а второй можно получить так :
2) Ю
Ю cb Ю acb.
Этим выводам соответствуют разные синтаксические деревья и разборы :
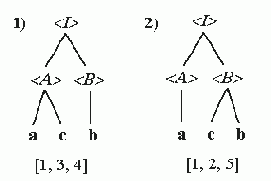
Следующая грамматика также допускает построение одной и той же цепочки с помощью двух выводов, имеющих разные синтаксические деревья.
Г1. 11:
Vт = {0, +}, Va = {},
R = { ® 0,
®
+ 0,
® 0 +
}.
Два вывода этой грамматики, порождающие одинаковые цепочки, имеют вид:
1) Ю
+ 0 Ю + 0 + 0 Ю 0 + 0 + 0,
2) Ю 0 + Ю 0 + 0 + Ю 0 + 0 + 0,
а синтаксические деревья, соответствующие этим выводам, можно изобразить так:
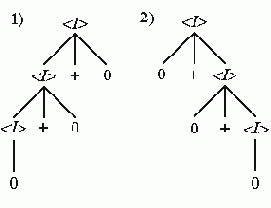
Рассмотренное свойство грамматик называется неоднозначностью. Оно может быть определено следующим образом.
| Определение. Цепочка языка L(Г) называется неоднозначной, если для её вывода существует более чем одно синтаксическое дерево. Если грамматика Г порождает неоднозначную цепочку, то она называется неоднозначной. |
Неоднозначность может существовать не только в искусственных языках. Хорошо известно, что в естественных языках могут быть предложения, допускающие неоднозначное написание. Например, "Пальто испачкало окно". В этой фразе не ясно, что является подлежащим, а что дополнением. Другим примером служит английская фраза: "They are flying planes", которая может быть понята двояко: "Они пилотируют самолет" или : Это летящие самолеты".
Свойство неоднозначности является крайне нежелательным для искусственных языков, поскольку оно не позволяет однозначным образом восстановить дерево вывода по заданной цепочке языка.
В общем случае можно сделать следующий вывод:
1) каждой цепочке, выводимой в грамматике, может соответствовать одно или несколько синтаксических деревьев,
2) каждому синтаксическому дереву могут соответствовать несколько выводов,
3) каждому синтаксическому дереву соответствует единственный правый и единственный левый выводы.
Кроме того, следует подчеркнуть, что один и тот же язык может быть получен с помощью различных грамматик.
| Определение. Две грамматики Г1 и Г2 называются эквивалентными, ecли они порождают один и тот же язык, т.е. L(Г1) = L(Г2). |
Описание списков
В качестве первых примеров рассмотрим построение грамматик для последовательностей символов и последовательностей символов с разделителями. Такие последовательности часто называют списками.
1) Обозначим элемент последовательности a. Простейшая последовательность может состоять из одного элемента a. Все другие последовательности могут быть получены путем приписывания к уже построенной последовательности еще одного элемента. Если обозначить построенную часть последовательности нетерминальным символом
Определение формальной грамматики и языка
Изучение предмета начнем с определения первичных понятий.
Первичные понятия
| Определение. Конечное множество символов, неделимых в данном рассмотрении, называется словарем или алфавитом, а символы, входящие в множество, - буквами алфавита. |
Например, алфавит A = {a, b, c, +, !}
содержит 5 букв, а алфавит B = {00, 01, 10, 11}
содержит 4 буквы, каждая из которых состоит из двух символов.
| Определение. Последовательность букв алфавита называется словом или цепочкой в этом алфавите. Число букв, входящих в слово, называется его длиной. |
Например, слово в алфавите A a=ab++c
имеет длину l(a) = 5, а слово в алфавите B b=00110010 имеет длину l (b) = 4.
Если задан алфавит A, то обозначим
A* множество всевозможных цепочек, которые могут быть построены из букв алфавита A. При этом предполагается, что пустая цепочка, которую обозначим знаком $, также входит в множество A*.

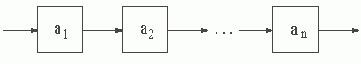
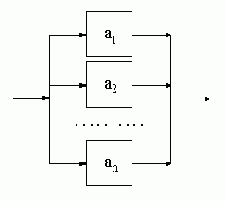
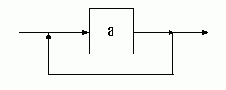
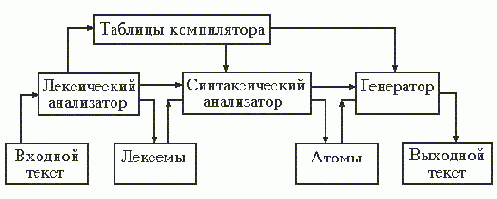

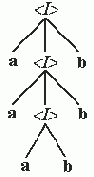
 Программирование: Языки - Технологии - Разработка
Программирование: Языки - Технологии - Разработка